相関係数、コサイン類似度の関係性
相関係数とコサイン類似度の違いと類似性について定量的に書かれているサイトがあまりなかったので、調べ見解をメモとして残す。
データ定義
今回扱うデータを以下のように定義する。
(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)
または、上記の2次元データをn次元データとみなし
\begin{align}
\boldsymbol{x} &= (x_1,x_2,\cdots,x_n)\top \\
\boldsymbol{y} &= (y_1,y_2,\cdots,y_n)\top
\end{align}
と表現することにする。
相関係数
相関係数は以下のように定義されている。
\begin{align}
Corr(\boldsymbol{x},\boldsymbol{y}) &= \frac{(\boldsymbol{x} - \bar{\boldsymbol{x}})\top(\boldsymbol{y} - \bar{\boldsymbol{y}})}{\sqrt{(\boldsymbol{x} - \bar{\boldsymbol{x}})\top(\boldsymbol{x} - \bar{\boldsymbol{x}})}{\sqrt{(\boldsymbol{y} - \bar{\boldsymbol{y}})\top(\boldsymbol{y} - \bar{\boldsymbol{y}})}}}
\end{align}
注)
\bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i\\
\bar{y} = \frac{1}{n}\sum_{i=1}^{n} y_i\\
\bar{\boldsymbol{x}} = (\bar{x},\bar{x},\cdots,\bar{x})\top\\
\bar{\boldsymbol{y}} = (\bar{y},\bar{y},\cdots,\bar{y})\top
と定義する。
コサイン類似度と比較するために、ベクトルの内積で書いたが、
\begin{align}
Corr(\boldsymbol{x},\boldsymbol{y}) &= \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2}\sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}}
\end{align}
と表現することもできる。
コサイン類似度
コサイン類似度は以下のように定義されている。
\begin{align}
Cossim(\boldsymbol{x},\boldsymbol{y}) &= \frac{\boldsymbol{x}\top\boldsymbol{y}}{\sqrt{\boldsymbol{x}\top\boldsymbol{x}}{\sqrt{\boldsymbol{y}\top\boldsymbol{y}}}}
\end{align}
また、以下のように表現することもできる。
\begin{align}
Cossim(\boldsymbol{x},\boldsymbol{y}) &= \frac{\sum_{i=1}^n x_i y_i}{\sqrt{\sum_{i=1}^n x_i^2} \sqrt{\sum_{i=1}^n y_i^2}}
\end{align}
違いと類似性
調べた際に気がついた相関係数とコサイン類似度の違いについて言及する。
違い①
import numpy as np
np.random.seed(0)
x = np.random.rand(100)
y = np.random.rand(100)
上記のように、0.0以上、1.0未満の一様分布から100個のデータを得たものを$x,y$とする。
相関係数は0あたりになることが予想される。
以下のように相関係数を計算する。
np.corrcoef(x, y)[0][1]
結果は-0.06610711104791324と返ってくる。
一方、コサイン類似度は以下のように定義でき、計算すると
def cossim(v1, v2):
return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))
cossim(x,y)
結果は0.7402807972603874と返ってくる。
これは、データがすべて正の値であるので、乱数を発生させているにも関わらず、高い(何をもって高いとするのかはおいておいて)類似度を得てしまう。
cossim(x-np.mean(x),y-np.mean(y))
しかし、上記のように平均値で引いてやれば、相関係数と同じ結果になることは前述した式を見れば明らかで、
結果は-0.06610711104791324と返ってくる。
違い②
先程は、100次元で考えたが、次は2次元で考えることにする。
import numpy as np
np.random.seed(0)
x = np.random.rand(2)
y = np.random.rand(2)
相関係数は
np.corrcoef(x, y)[0][1]
を計算すると-1を返す。
基本、相関係数を2次元で計算すると、平均値を引く変換によって第2象限、第4象限に点が変換されるので、-1 or 1しか得られない。(注:原点に変換された場合は分母が0になるのでnanを返す)
一方、コサイン類似度は
cossim(x,y)
結果は0.9836164444783699を返す。
類似性
データの平均が大体0で次元が高い場合相関係数とコサイン類似度は似た関係を示す。
相関係数と次元
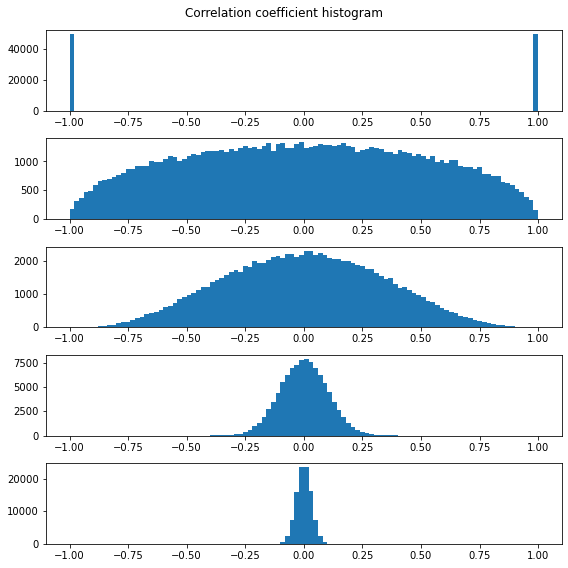
最後に、次元が上がることによって、相関係数はどのように変化するかということについて言及する。
変数は独立で標準正規分布に従うとする。
ここでは、2,5,10,100,1000次元の相関係数を100000回繰り返すことでヒストグラムを生成した。
import numpy as np
import matplotlib.pyplot as plt
def get_coef_array(count, dim):
coef = []
for i in range(count):
vec_1 = np.random.randn(dim)
vec_2 = np.random.randn(dim)
coef.append(np.corrcoef(vec_1, vec_2)[0][1])
return np.array(coef)
dim_lst = [2,5,10,100,1000]
count = 100000
fig, axs = plt.subplots(len(dim_lst),figsize=(8, 8))
fig.suptitle('Correlation coefficient histogram')
for i, dim in enumerate(dim_lst):
coef = get_coef_array(count, dim)
axs[i].hist(coef,range=(-1, 1),bins=100)
plt.tight_layout()
plt.show()
結果は上図のようになり、
次元が高い(データ数が多い)ほど相関係数が低く算出される確率が高くなる。
また、相関係数の検定統計量は統計WEB 26-3. 相関係数によれば、$n$をサンプルサイズ、$r$を相関係数とした場合以下のように表すことができるらしい。
\begin{align}
t &= \frac{\left|r\right|\sqrt{n-2}}
{\sqrt{1-r^{2}}}
\end{align}
それ以外にも、相関係数の有意検定を行いたい場合はpermutation testを行う方法もある。
最後に
相関係数のp値が上記で得られるという理由がいまいち分からなかったので、今後調べていきたい。
誤りがあれば、ご指摘お願い致します。
参考
Qiita【Python NumPy】コサイン類似度の求め方
Qiita 相関係数とコサイン類似度
cos類似度の次元の呪い
統計WEB 26-3. 相関係数