【Python NumPy】コサイン類似度の求め方

算出式

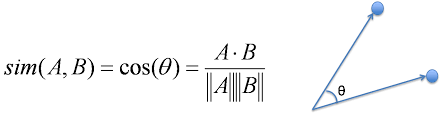
コサイン類似度は、2つのベクトル間の角度のコサインを使用して、ベクトルの類似性を測定する方法です。値は-1（完全に逆）から1（完全に一致）までの範囲で、0は無関係を意味します。

具体例

	X(vector)	Y(vector)
属性値a	0.789	0.832
属性値b	0.515	0.555
属性値c	0.335	0
属性値d	0	0

cos(X, Y) = (0.789 × 0.832) + (0.515 × 0.555) + (0.335 × 0) + (0 × 0) ≒ 0.942

対応コード

関数

import numpy as np

def cos_sim(v1, v2):
    return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

実行

X = np.array([0.789, 0.515, 0.335,0])
Y = np.array([0.832, 0.555,0,0])

# cos(X,Y) = (0.789×0.832)+(0.515×0.555)+(0.335×0)+(0×0)≒0.942
print(cos_sim(X, Y))  #=> 0.9421693704700748

numpyを使用しない版

※要動作確認

# Define a function to calculate the dot product of two vectors.
def dot_product(a, b):
    return sum(x * y for x, y in zip(a, b))

# Define a function to calculate the magnitude (norm or length) of a vector.
def magnitude(vector):
    return sum(x**2 for x in vector) ** 0.5

# Define a function to calculate the cosine similarity between two vectors
# using the dot product and magnitudes.
def cosine_similarity(a, b):
    dot_prod = dot_product(a, b)
    mag_a = magnitude(a)
    mag_b = magnitude(b)
    similarity = dot_prod / (mag_a * mag_b)
    return similarity

# Example vectors
vector_a = [1, 2, 3]
vector_b = [4, 5, 6]

# Calculate cosine similarity
similarity = cosine_similarity(vector_a, vector_b)
print(f"Cosine similarity between 'vector_a' and 'vector_b': {similarity}")