次世代の畳み込み？！CondConv

はじめに

日課のarXiv論文のチェックをしていたところ、Microsoftから興味深い論文¹が出ていました。

Microsoftから動的にConvの重みを変えるDynamic Convolutionの提案。重み自体を出力するのではなく、複数のConvの線型結合の係数を出力する（Attention)。実はGoogleからもCondConvという同様のアプローチが提案されていて（NIPS'19）熱い！ https://t.co/M36wbog1nm https://t.co/lwznevSy2y pic.twitter.com/vNZH6M4CL3

— Yusuke Uchida (@yu4u) December 10, 2019

チラ見してみると、積ん読していたGoogle Brainから出ている論文CondConv²の論文とほぼ同じような主張をしていたので、CondConvのほうを改めて読んでみたところ、汎用的でありながら単に導入するだけで（CNNに限らない）様々なDNNモデルの精度を改善できる可能性があると感じました。せっかくなので2つの論文を合わせて論文を読んでみます。CondConvは、初版がarXivに4月に投稿されており、更にNIPS'19に採録されているので、こちらをメインにします。

端的には、入力に応じてレイヤ内に保持している複数の畳み込み（全結合層）のパラメータの線型結合により、入力に応じて動的に畳み込み（全結合層）のパラメータを生成するレイヤを提案しています。

• Pros
  • 通常の畳み込みや全結合層をそのまま置き換えることができる汎用的なレイヤ
  • 僅かな計算量の増加で性能向上が見込める
• Cons
  • モデルのパラメータはかなり増加する
  • パラメータが多くなるため学習に時間がかかる可能性がある。もしかしたら安定しないかも
  • 畳み込み層に適用する場合には、サンプル毎に異なる畳み込みを行うため学習効率が悪くなる

空いていたので、Deep Learning論文紹介 Advent Calendar 2019の11日目の記事にしてしまいました。前の記事は【論文読み】クラスタリングが無くなる日？で、半教師あり学習の最新手法が紹介されています。

背景

どちらの論文も、エッジデバイスでの推論のような、精度と速度が求められるモデルを構築することを目的としています。現在、このような目的のために広く利用されているのは、MobileNetで利用されているseparable convolutionといったdepthwise convolutionを利用したモジュールです。このような軽量モジュールについては、こちらの記事や、スライドで解説を行っているので、興味がある方は是非参照してみてください。

さて、これらのモジュールの有効性は広く確かめられていますが、入力に対して常に同じ処理を行っているという点で改善の余地があると考えられます。これに対し、入力に応じて処理を変えるようなモデルも提案されており、Routing networks³, Blockdrop⁴, SkipNet⁵といった手法が提案されています。Routing networksでは、入力に応じて行う処理を動的にスイッチしています。BlockDropやSkipNetでは、高速化を目的として、入力に応じてresidual blockを動的にスキップしています。この動的なルーティングはどれも強化学習を用いて学習されています。

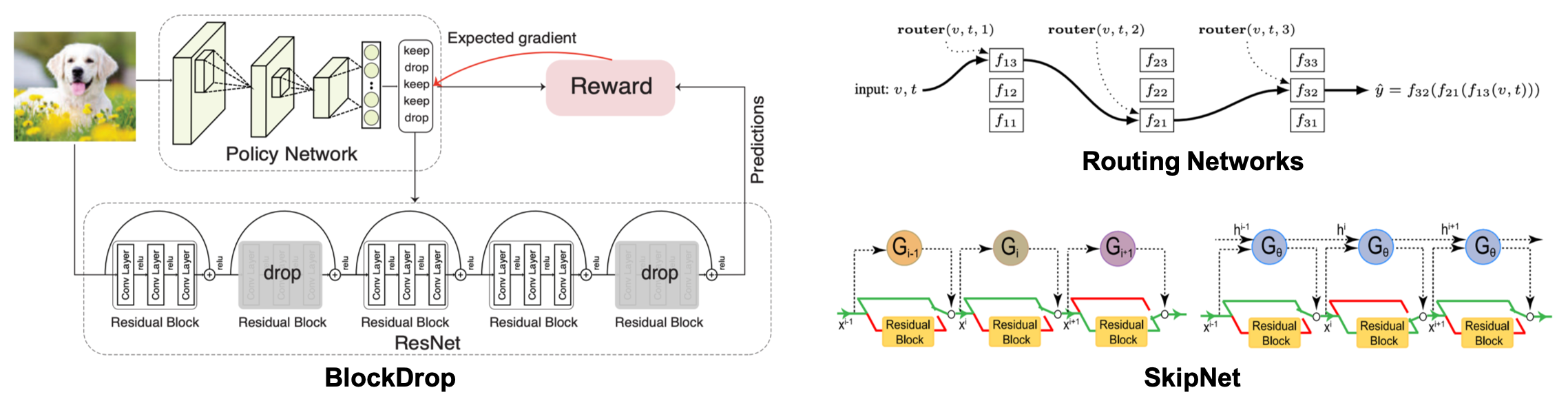
これらの手法では、入力に対し動的にネットワークの構造が変化しますが、それぞれの処理で利用されている重みは同じです。CondConvでは入力に応じて重み自体を適応的に変化させることで、より効率的なモデルを構築できる可能性があります。また、モデル単体をend-to-endに学習できるという点もメリットです（NASでトレンドのようにsoftmax等を利用してend-to-endで学習できるものもあると思いますが）。

ニューラルネットワークの重み自体を生成するモデルに関する研究も存在^{6 7}しますが、サンプル毎に適応的に重みを変化させるような手法ではありません。単純に考えると、畳み込みの重み自体を入力に応じて生成するアプローチが一番straightforwardかつ汎用性がありそうな気がしますが、これまで成功例を見たことがないので、うまくいくには何かが足りない可能性があります。このCondConvも、後述のように入力に不変なパラメータの混合という成約を入れているからこそ性能が出たのではないかと考えられます。

CondConv

さて、実際のCondConvについてですが、それぞれの論文の図が端的に手法を説明しています。左がCondConvの論文²から、右がDynamic Convolution（名称として良くない）の論文¹から引用した図です。アプローチ自体は本質的には同じですね。

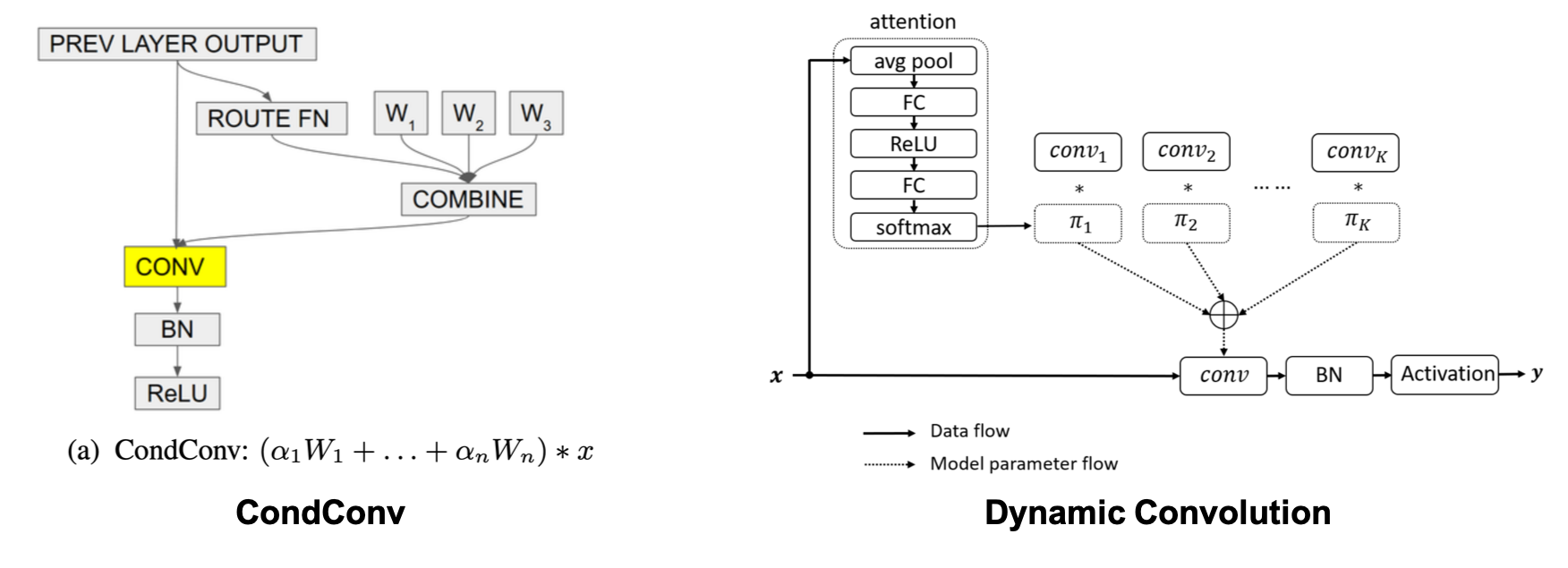
入力$x$に対し、通常のconvolutionは入力$x$に不変なパラメータ$W$で畳み込みを行い出力$y = \sigma(W * x)$を得ます。ここで$\sigma$は活性化関数です。
これに対し、CondConvでは、入力$x$に不変な複数の畳み込みのパラメータ$W_1, W_2, \cdots, W_n$を保持しておき、入力$x$によって変化する混合係数$\alpha_1, \alpha_2, \cdots, \alpha_n$を求め、これらから新たな畳み込みのパラメータ$W$を求めます。そしてそのパラメータ$W$を用いて畳み込みを行い、出力$y = \sigma((\alpha_1 W_1 + \alpha_2 W_2 + \cdots + \alpha_n W_n) * x)$を得ます。この出力は下式の通り、パラメータ$W_1, W_2, \cdots, W_n$でそれぞれ個別に畳み込みを行い、その出力を後から重み$\alpha_1, \alpha_2, \cdots, \alpha_n$で足し合わせる場合 (mixture of experts) と同じになります。
$$
\sigma((\alpha_1 W_1 + \alpha_2 W_2 + \cdots + \alpha_n W_n) * x) = \sigma(\alpha_1 (W_1 * x) + \alpha_2 (W_2 * x) + \cdots + \alpha_n (W_n * x))
$$
CondConvのメリットは、このmixture of expertsの効果を、計算量としてはほぼ1回の畳み込みの処理で行える点にあります。

さて、入力$x$によって変化する混合係数$\alpha$はどのように得られるのでしょうか。CondConvでは非常にシンプルに、入力$x$に対しGlobalAveragePoolingを行った後、全結合層を通し、最後にsigmoid関数を適用するという形になっています。下式で$R$は全結合層の重み行列です。
$$
r(x) = \mathrm{sigmoid}(\mathrm{GlobalAveragePooling}(x) ; R)
$$
一方、Dynamic Convolutionのほうは、GlobalAveragePooling、全結合層、ReLU、全結合層、softmaxと、SEモジュールのように一度活性化関数をはさんで全結合層が2つあります。最初の全結合層でチャネル数を1/4にし、最後の全結合層で出力チャネル数を畳み込みの数$n$にしています。なお、CondConvでも全結合層を増やす実験が行われており、入力チャネル数と同じ出力チャネル数を持つ全結合層を追加すると僅かに精度が向上し、入力チャネル数の1/8や8倍にしたケースでは精度が低下することが報告されています。

CondConvでは近いレイヤの混合係数がある程度シェアされている方が性能が良いことが主張されており、MobileNetのseparable convolution内のdepthwise/pointwise convolutionの混合係数や、EfficientNetの同じinverted bottleneck blockに属するレイヤの混合係数はお互いシェアされている実装となっているようです。

以上のようなCondConvを通常のconvolutionやdepthwise convolutionの代わりに利用することで、僅かな計算量の増加で様々なベースネットワークのクラス分類等の精度を改善することが期待できます。1点デメリットがあるとすると、畳み込み自体の計算量は増えないものの、複数の畳み込みのパラメータを保持する関係上、パラメータ数が1つのCondConv内に保持する畳み込みの個数に比例して増加してしまう点が挙げられます。ゆくゆくはこのパラメータの削減等も提案されていくのでしょうか。

学習

学習自体は、どちらもbackprop可能なレイヤとして実装できるため、通常の確率的勾配降下法で学習が可能です。ただし、CondConvの論文には記載の通り、畳み込みのパラメータを足し合わせる場合には、サンプル毎に畳み込みのパラメータが異なってしまうので、通常の畳み込み層で実装する場合にはミニバッチサイズ1の学習にしないといけない点が課題です。これでは学習効率が悪いので、CondConv内の畳み込み数が少ない場合には、敢えて畳み込みを行った後に出力を足し合わせるmixture of expertsの状態にしてミニバッチサイズを1より大きくして学習することを提案しています。この場合は逆に、利用メモリと計算量がCondConv内の畳み込みの数だけ大きくなってしまう課題があります。Dynamic Convolutionのほうでは特に言及されていなかったので、サンプル毎にconvolutionを個別に適用するレイヤとして実装されているのでしょうか。

混合係数の算出にsoftmaxを利用しているDynamic Convolutionでは、係数がスパースになるため各ステップで一部の畳み込みの重みのみがアップデートされることになり、学習の収束が遅いことが指摘されています。これに対応するため、softmaxに比較的大きめ（$T=30$）の温度パラメータを利用することを提案しています。

個人的には、softmaxの出力がスパースだからというより、mixture of expertsの重みを学習する系に共通する課題として、特定のexpertの学習が進むことでそのexpertの係数が高くなり、そのexpertばかり選ばれて学習されるという難しさがあると思っていて、その辺りでちゃんと学習できるのだろうかという懸念があります。
CondConvの論文にはその辺りの記載は特にありませんでした。代わりに、shake-shake⁸のアプローチを採用し、各expertをランダムにdropさせながら学習する旨があったので、これで吸収されているのかもしれません。CondConvでは、他にも学習時にdropout, AutoAugment, mixupも利用しており、パラメータ数が増えることによるoverfitting回避しています。このように過度のaugmentationを利用しないと性能が出ないとすると使いづらいですね。

実験結果

どちらの論文においても、MoibleNetやResNetといったベースネットワークの畳み込みを、CondConvに置き換えることで、僅かな計算量の増加で、1〜数ポイントのImageNetでの精度向上を確認しています。Object detectionやkeypoint detectionタスクでの有効性も確認されています。

CondConvの論文より。CondConv内の畳み込みの個数を増加させた場合に、一定数まで精度と計算量のトレードオフが改善していることが分かります。

実装

実装は現状、tensorflowの公式実装のみ存在するようです。学習はともかくレイヤの実装自体は簡単にできそうなので、是非再現してみましょう！

まとめ

今回はMicrosoftとGoogle Brainが同時期（と言うにはちょっと時間差がある）にほぼ同様の提案をした入力に応じて動的にパラメータを変化させるレイヤの紹介をしました。いかがだったでしょうか？

1. Y. Chen, X. Dai, M. Liu, D. Chen, L. Yuan, and Z. Liu, "Dynamic Convolution: Attention over Convolution Kernels," in arXiv:1912.03458, 2019. ↩ ↩²

2. B. Yang, G. Bender, Q. V. Le, and J. Ngiam, "CondConv: Conditionally Parameterized Convolutions for Efficient Inference," in Proc. of NIPS, 2019. ↩ ↩²

3. C. Rosenbaum, T. Klinger, and M. Riemer, "Routing Networks: Adaptive Selection of Non-linear Functions for Multi-task Learning," in Proc. of ICLR, 2018. ↩

4. Z. Wu, T. Nagarajan, A. Kumar, S. Rennie, L. Davis, K. Grauman, and R. Feris, "Blockdrop: Dynamic Inference Paths in Residual Networks," in Proc. of CVPR, 2018. ↩

5. X. Wang, F. Yu, Z. Dou, T. Darrell, and J. Gonzalez, "SkipNet: Learning Dynamic Routing in Convolutional Networks," in Proc. of ECCV, 2018. ↩

6. D. Ha, A. Dai, and Q. V Le, "Hypernetworks," in Proc. of ICLR, 2017. ↩

7. Z. Liu, H. Mu, X. Zhang, Z. Guo, X. Yang, T. Cheng, and J. Sun, "MetaPruning: Meta Learning for Automatic Neural Network Channel Pruning," in Proc. of ICCV’19. ↩

8. X. Gastaldi, "Shake-Shake Regularization of 3-branch Residual Networks," in Proc. of ICLR 2017 Workshop, 2017. ↩