はじめに
ニューラルネットワークが持つ欠陥「破滅的忘却」を回避するアルゴリズムをDeepMindが開発したらしいので、元論文を読んでみた。
Overcoming catastrophic forgetting in neural networks
https://arxiv.org/abs/1612.00796
- Introの最初から汎用人工知能とかいきなり出てくるのでおおっと思うが、やってることはめちゃくちゃシンプル
- 端的に言えば学習したニューラルネットのパラメータのそのタスクに対する重要度がフィッシャー情報行列で測れるよ
- 脳神経科学系の単語が結構出てくるので、専門家がいるのかな?とはいえこの背景は後付で、アルゴリズムが先なんじゃないかな…
- 元の論文では数式を端折っている箇所があるので、適宜補完しつつ、直感的解釈とかは勝手に入れている。論文の流れにはそこまで沿っていない
- 不正確・間違っている箇所は指摘をお願いします!
背景
汎用人工知能は多数の異なるタスクをこなすことが求められる。これらのタスクは明示的にラベル付けされていなかったり、突然入れ替わったり、長い間再び発生しなかったりするため、逐次的に与えられるタスクを、以前に学習したタスクを忘れることなく学習するcontinual learning(継続学習)が重要となる。
しかしながら、人工ニューラルネットワークにおいては、現在のタスク(e.g. task B)に関する情報を扱うと、以前のタスク(e.g. task A)に関する情報を急に失ってしまうcatastrophic forgetting(破滅的忘却)が発生してしまうことが課題となっている。現状の破滅的忘却に対する対応策は、全てのタスクに関するデータを予め揃え、同時にすべてのタスクを学習する(各タスクのデータを細切れに並べて学習させる)multitask learningである。
もしタスクが逐次的にしか与えられない場合、データを一時的に記憶し、学習時に再生する(system-level consolidation; システムレベルの記憶固定)しかないが、タスク数に比例したメモリと再生時間が必要となるため、非現実的である。
他方、哺乳類の脳は、大脳新皮質の神経回路に獲得した知識を守ることで、破滅的忘却を防いでいるのではないかということを示唆する証拠が見つかっている。新しい知識を獲得するとシナプスの一部が強化され、数ヶ月間その知識が維持される。すなわち、このシナプスの保護を支援する神経機構が、タスクの性能の維持に重要であるということである。
このように、継続学習はtask-specific synaptic consolidationにより実現されていると解釈することができる。そこでは、タスクに対する知識は、学習時に非可塑的になったシナプスの割合に比例して維持される。
本論文では、このsynaptic consolidationに着想を得たelastic weight consolidation (EWC) を提案する。このアルゴリズムでは、以前のタスクにおいて重要であった特定の重みの学習を遅くする(非可塑的にする)ことで、以前のタスクを忘れることなく逐次学習を実現する。
(TODO)synaptic consolidationとsystem consolidationについて読む
https://en.wikipedia.org/wiki/Memory_consolidation
Elastic Weight Consolidation (EWC)
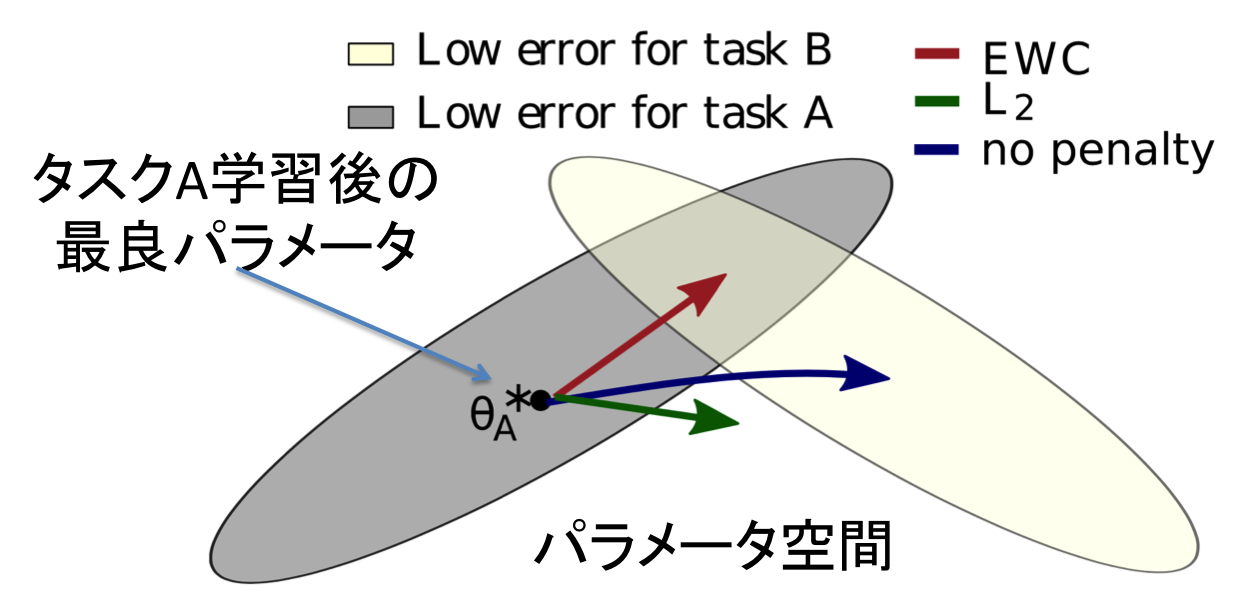
EWCのアイディアを下記の図により説明する。
上記の図において、灰色はタスクAのエラーが小さくなる領域、クリーム色はタスクBのエラーが小さくなる領域を示している。今、タスクAを学習し、パラメータ$\theta_A^{*}$を得たとする。この後、別のタスクBを学習することを考える。
タスクAについて何も考慮せずにタスクBを学習すると、パラメータはタスクBの最良パラメータへ移動し、タスクAについて破滅的忘却が発生する(青の矢印)。
他方、パラメータがなるべく$\theta_A^{*}$から変化しないようにタスクBを学習することもできる。例えば、$\lambda ||\theta - \theta_A^{*}||^2_2$をロスに組み込むことが考えられる。しかしながら、この場合、タスクAおよびタスクBのどちらもエラーが下がらない領域にパラメータが移動する可能性がある(緑の矢印)
これに対し、EWCは、重要な重みのみを変化させないことで、タスクAのエラーが小さくなる領域を通りながら学習を進めるため、タスクAに関する知識を失うことなく、新たなタスクBの知識を習得することができる(赤の矢印)
上記の重要な重みを定義するために、確率的な観点からニューラルネットの学習を考える。パラメータの最適化は、データ$\mathcal{D}$が与えられた際に、最も尤もらしいパラメータを見つけることと同等である。このとき最大化すべき事後確率$p(\theta|\mathcal{D})$は、ベイズの定理により、下記のように求められる。
p(\theta|\mathcal{D}) = \frac{p(\mathcal{D}|\theta) p(\theta)}{p(\mathcal{D})}
対数をとると、
\log p(\theta|\mathcal{D}) = \log p(\mathcal{D}|\theta) + \log p(\theta) - \log p(\mathcal{D})
ここで、データ$\mathcal{D}$は、タスクAのデータ$\mathcal{D}_A$と、タスクBのデータ$\mathcal{D}_B$から構成され、それぞれ独立に生成されると仮定すると、
\log p(\theta|\mathcal{D}) = \log \left( p(\mathcal{D}_A|\theta) p(\mathcal{D}_B|\theta) \right) + \log p(\theta) - \log \left( p(\mathcal{D}_A) p(\mathcal{D}_B) \right)
\log p(\theta|\mathcal{D}) = \log p(\mathcal{D}_A|\theta) + \log p(\mathcal{D}_B|\theta) + \log p(\theta) - \log p(\mathcal{D}_A) - \log p(\mathcal{D}_B)
\log p(\theta|\mathcal{D}) = \log p(\mathcal{D}_B|\theta) + \log p(\theta|\mathcal{D}_A) - \log p(\mathcal{D}_B)
となる。ここで、左辺はデータ全体が与えられた際の事後確率であるが、右辺はタスクBのロス関数$\log p(\mathcal{D}_B|\theta)$のみに依存している(ロス関数を$\mathcal{L}(\theta)$とすると、$\mathcal{L}(\theta) = - \log p(\mathcal{D}_B|\theta)$)。それ故、タスクAに関する全ての情報は事後確率$\log p(\theta|\mathcal{D}_A)$に吸収されており、どのパラメータがタスクAにとって重要かという情報も含まれているはずである。
ここで、真の事後分布を求めることは不可能なので、MackayのLaplace approximationに従い、この事後確率を平均が$\theta_A^{*}$、対角の精度行列がフィッシャー情報行列$F$の対角成分で与えられる多変量ガウス分布で近似する(精度行列が$F$⇔分散共分散行列$\Sigma = F^{-1}$)。
p(\theta | \mathcal{D}_A) = \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}}\exp \left( - \frac{1}{2} (\theta - \theta_A^* )^{\top} \Sigma^{-1} (\theta - \theta_A^* ) \right)
\log p(\theta | \mathcal{D}_A) = - \frac{1}{2} (\theta - \theta_A^* )^{\top} \Sigma^{-1} (\theta - \theta_A^* ) + \mathrm{const}
$\Sigma = F^{-1}$および$F$が対角であるという仮定を利用すると、下記を得る。
\log p(\theta | \mathcal{D}_A) = - \frac{1}{2} \sum_i F_{ii} (\theta_i - \theta_{Ai}^* )^2 + \mathrm{const}
これにより、タスクBを学習する際のEWCの目的関数は下記となる。
\mathcal{L}(\theta) = \mathcal{L}_B(\theta) + \frac{\lambda}{2} \sum_i F_{ii} (\theta_i - \theta_{Ai}^* )^2
ここで、$\mathcal{L}_B(\theta)$は、タスクBについてのみのロス関数、$\lambda$はこれまでのタスクが新しいタスクに対してどの程度重要かというパラメータである。これにより、フィッシャー情報行列$F$によって捉えられたパラメータの重要度を加味した逐次学習が可能となる。
実験では、MNISTのピクセルを、特定の順列で並び替えたデータを3種類作成し、それらを逐次的に学習させ、EWCが全てのタスクをちゃんと学習していることが示されている。また、強化学習についても実験が行われているが、ここでは省略する。
個人的な直感的理解
- 結局やりたいことは、タスクAで学習したパラメータ$\theta_A^*$をなるべく維持しながらタスクBを学習したい
- なるべく維持=$\ell_2$距離を小さくでは駄目。何故ならパラメータは多様体上にあり、適切な計量を考慮した測地線で距離を測らないといけない
- 確率分布における計量=フィッシャー情報行列
- KLダイバージェンスを2次の項までテイラー展開したものがフィッシャー情報行列
具体的なアルゴリズム
詳細が記載されていないが、恐らくタスクAを学習させ、収束させた後、フィッシャー情報行列$F$を求める。$F$の算出には、学習時と同じように学習サンプル$d_1, \cdots, d_N$を利用してパラメータの勾配を求める。サンプル数がどの程度必要であるかはよく分からない。$\nabla\theta_n$を$d_n$をbackpropして得られた勾配とすると、$F_{ii} = \frac{1}{N} \sum_{n=1}^N \nabla\theta_{ni}^2$と求められる。
$F$が求まれば、$\frac{\lambda}{2} \sum_i F_{ii} (\theta_i - \theta_{Ai}^* )^2$をロスに加えるだけ。
フィッシャー情報行列でパラメータの重要度を測るという意味では、例えば下記の論文とかも同じようなことをやっている気がする。
Towards the Limit of Network Quantization, ICLR’17.
https://arxiv.org/abs/1612.01543
上記論文では、データ量削減のため、パラメータを量子化する必要があり、パラメータの重要度を考慮した量子化を提案している。具体的には、ロス関数を2次までテイラー展開して近似すると、ヘッシアンがパラメータが少しずれたときのロスの増加を表す重要度となる、ということで同じことをしているイメージ。
参考
解説記事
https://rylanschaeffer.github.io/content/research/overcoming_catastrophic_forgetting/main.html
http://www.inference.vc/comment-on-overcoming-catastrophic-forgetting-in-nns-are-multiple-penalties-needed-2/
TensorFlow実装
https://github.com/ariseff/overcoming-catastrophic