比較的分かりやすいし、それなりに速いし、実装も楽。みんな大好き k-means 法。
今回はそんな k-means 法を、 C# の LINQ(+MoreLINQ) で書いてみました。
k-means 法について
簡単に言うと、各データ点の、自分が所属するクラスタ中心との二乗誤差の総和を、貪欲に最小化する手法です。
クラスタ数 $k$ 、あるクラスタ $i$ に所属するデータ点の集合 $S_i$ として、式で書くとこんな感じ。
\arg \min \sum_{i=1}^k \sum_{x \in S_i} ||x - \mu_i||^2
もう少し詳しく知りたい人には、神嶌先生の資料が分かりやすいです。
イメージをつかむなら、「K-means 法を D3.js でビジュアライズしてみた」が k-means 法を step-by-step で実行できて理解の助けになるかと思います。
k-means 法のアルゴリズム
計算の流れは、以下の通り。
- データ点からランダムに k 個の点をクラスタ中心の初期値として取る。
- 以下の 2 ステップを収束するまで繰り返す。
- 各データ点について、自身に最も近いクラスタに割り当てる。
- 各クラスタについて、所属するデータ点の平均を計算して新しいクラスタ中心とする。
k-means 法の実装
今回対象とするデータは、簡単のため double 型の 1 次元データとします。
データ構造は以下のようにします。n はデータ点の数、 k はクラスタ数です。
| 変数 | 型 | 長さ | 中身 |
|---|---|---|---|
| data | double[] | n | クラスタリングしたいデータ。今回は double 型の配列。 |
| assignments | int[] | n | 各データ点がどのクラスタに属するか。 {0, 1, ..., k-1} の整数値を取る。 |
| means | double[] | k | 各クラスタの中心。各クラスタに所属するデータの平均をとったもの。 data 同様 double 型の配列 |
加えて、 data と assignments については、同じ添字は同じデータ点を指すこととします。
ソースコードはこんな感じ。
public static Tuple<double[], int[]> KMeans(double[] data, int k)
{
// 1. データ点からランダムに k 個のクラスタ平均を初期値として取る。
var rand = new Random();
var means = data.OrderBy(v => rand.Next()).Take(k).ToList();
// 2. 収束判定のためにループ外に assignments 変数を持っておく。
var assignments = new int[data.Length];
// 2. 収束するまで繰り返す。
while (true)
{
// 2. 収束判定のために 1 つ前の状態をコピー。
var prevAssignments = assignments.Select(v => v).ToArray();
// 2.1. 各データ点について、自身に最も近いクラスタに割り当てる。
assignments = data.Select(v => means.IndexOf(means.MinBy(m => Math.Pow(v - m, 2)))).ToArray();
// 2. 収束していたら計算終了。
if (Enumerable.Range(0, data.Length).All(i => assignments[i] == prevAssignments[i])) break;
// 2.2. 各クラスタについて、所属するデータ点の平均を計算して新しいクラスタ平均とする。
means = means.Select((m, i) => data.Where((v, j) => i == assignments[j]).DefaultIfEmpty(m).Average()).ToList();
}
return Tuple.Create(means.ToArray(), assignments);
}
括弧、コメント、関数の呼び出し・戻り値を除いた、純粋にアルゴリズムに関係している部分は 8 行で書けています。
それぞれについて説明していきます。
1,2 行目
// 1. データ点からランダムに k 個のクラスタ平均を初期値として取る。
var rand = new Random();
var means = data.OrderBy(v => rand.Next()).Take(k).ToList();
まず、上記の部分ではクラスタ平均の初期値を取っています。
具体的には、まず data.OrderBy(v => rand.Next()) で、ランダムな値についてソートすることで、元の data の要素をシャッフルをした配列(正確には IEnumerable オブジェクト)を得ます。次に、 .Take(k) でその最初の k 個を取ることで、疑似的に「データ点からランダムに k 個の点をクラスタ中心の初期値として取る」という処理を再現しています(完全にはランダムになっていないですが、 k-means 法ではそれほど気にする必要はないでしょう)。
(2017/2/7 追記) @ozwk さんよりご指摘を受けましたが、乱数の生成に Guid を使うと、乱数のジェネレータを変数に持っておく必要がないので、以下のように 1 行で書くことができます。
var means = data.OrderBy(v => Guid.NewGuid()).Take(k).ToList();
3 行目
// 2. 収束判定のためにループ外に assignments 変数を持っておく。
var assignments = new int[data.Length];
今回はデータ点に対するクラスタへの割り当て (assignments) が変化しなくなったら収束したとみなすので、収束判定のためにループ外で assignments を宣言しています。 means を収束判定に使用してもよいのですが、そうすると判定のときの式が厳密ではなくなるのでこちらの方が良いでしょう。
4 行目
// 2. 収束するまで繰り返す。
while (true)
繰り返し部分です。今回は、 while ループを回して収束したら break する形にします。
5 行目
// 2. 収束判定のために 1 つ前の状態をコピー。
var prevAssignments = assignments.Select(v => v).ToArray();
収束判定の準備です。単純に代入しただけだと shallow copy になってしまう (assignments を変更すると prevAssignments も変更される) ので、 deep にするために .Select(v => v) を挟んでいます。こうすることで、 assignments とは別の配列のインスタンスが作られます。
6 行目
// 2.1. 各データ点について、自身に最も近いクラスタに割り当てる。
assignments = data.Select(v => means.IndexOf(means.MinBy(m => Math.Pow(v - m, 2)))).ToArray();
各データ点について、 means.IndexOf(means.MinBy(m => Math.Pow(v - m, 2))) で、中心との距離が最小になるようなクラスタの means 配列内でのインデックスを取得しています。 MinBy には MoreLinq パッケージが必要です。
7 行目
// 2. 収束していたら計算終了。
if (Enumerable.Range(0, data.Length).All(i => assignments[i] == prevAssignments[i])) break;
収束判定の部分です。全てのデータ点について、どの点でも割り当てられるクラスタが変化していなかったら (収束していたら) 、ループを抜けます。
8 行目
// 2.2. 各クラスタについて、所属するデータ点の平均を計算して新しいクラスタ平均とする。
means = means.Select((m, i) => data.Where((v, j) => i == assignments[j]).DefaultIfEmpty(m).Average()).ToList();
最後に、 means.Select((m, i) => で、各クラスタの中心 m と添字 i について、data.Where((v, j) => i == assignments[j]) で i 番目のクラスタに割り当てられているデータ点を抽出し、 .Average() で平均を取り、新たなクラスタ中心とします。 .DefaultIfEmpty(m) は、もしどの点も割り当てられないようなクラスタ中心ができてしまったら、そのクラスタ中心については 1 つ前の値をそのまま保持するという設定をしています。
クラスタリング結果
上記のようなコードで、ひとまず double 型についてはクラスタリングができるようになりました。さっそく実行してみましょう。
var data = new double[] {1, 2, 3, 3, 5, 6, 8, 9, 100};
var results = KMeans(data, 4);
var assignments = results.Item2;
for (var i = 0; i < data.Length; i++)
{
Console.WriteLine($"value:{data[i],3}, cluster:{assignments[i],2}");
}
以下のような結果が出ました。 value がクラスタリング対象の実数値、 cluster が割り当てられるクラスタのインデックスを指します。一応きちんとクラスタリングできていそうです。
value: 1, cluster: 3
value: 2, cluster: 2
value: 3, cluster: 2
value: 3, cluster: 2
value: 5, cluster: 1
value: 6, cluster: 1
value: 8, cluster: 1
value: 9, cluster: 1
value: 100, cluster: 0
おまけ(2次元のデータの場合)
1 次元データだけだとやはり映えないので 2 次元の System.Numerics.Vector2 型のものも載せておきます。この場合、自分で拡張メソッドを書く必要があるので、 8 行ではなくなってしまいますが……。
// Vector2 には System.Numerics.Vectors が必要(ライセンスに同意する必要あり)。
public static Tuple<Vector2[], int[]> KMeans(Vector2[] data, int k)
{
var rand = new Random();
var means = data.OrderBy(v => rand.Next()).Take(k).ToList();
var assignments = new int[data.Length];
while (true)
{
var prevAssignments = assignments.Select(v => v).ToArray();
assignments = data.Select(v => means.IndexOf(means.MinBy(m => (v - m).LengthSquared()))).ToArray();
if (Enumerable.Range(0, assignments.Length).All(i => assignments[i] == prevAssignments[i])) break;
means = means.Select((m, i) => data.Where((v, j) => i == assignments[j]).DefaultIfEmpty(m).Average()).ToList();
}
return Tuple.Create(means.ToArray(), assignments);
}
public static class Extensions
{
public static Vector2 Average(this IEnumerable<Vector2> self)
{
var array = self as Vector2[] ?? self.ToArray();
return array.Aggregate(Vector2.Zero, (v1, v2) => v1 + v2)/array.Length;
}
}
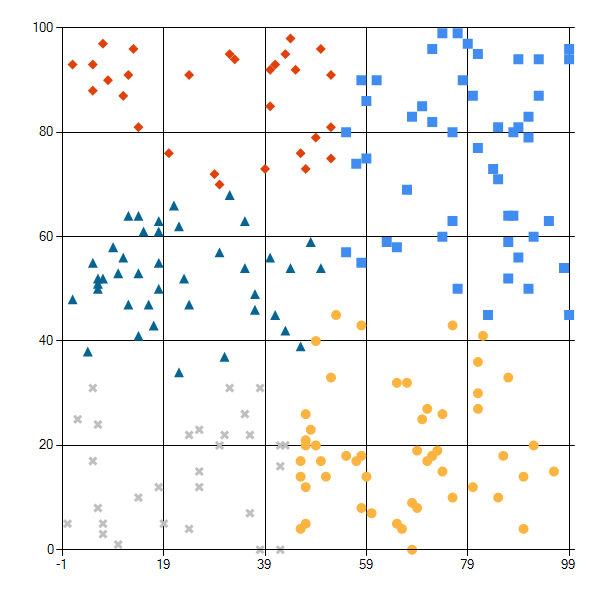
以下の条件でクラスタリングした結果は下図のような感じ。
- データ数: 200
- クラスタ数: 5
問題なさそうです。
おわりに
というわけで、 8 行で k-means 法の実装でした。
おかしなところ等あればご指摘いただけると幸いです!