書いたこと
- 3次元空間の頂点をある軸を中心に回転させる時に使われる回転公式について
- ロドリゲスの回転公式
- クォータニオンの回転公式
- 球面線形補間が必要になる理由について
はじめに
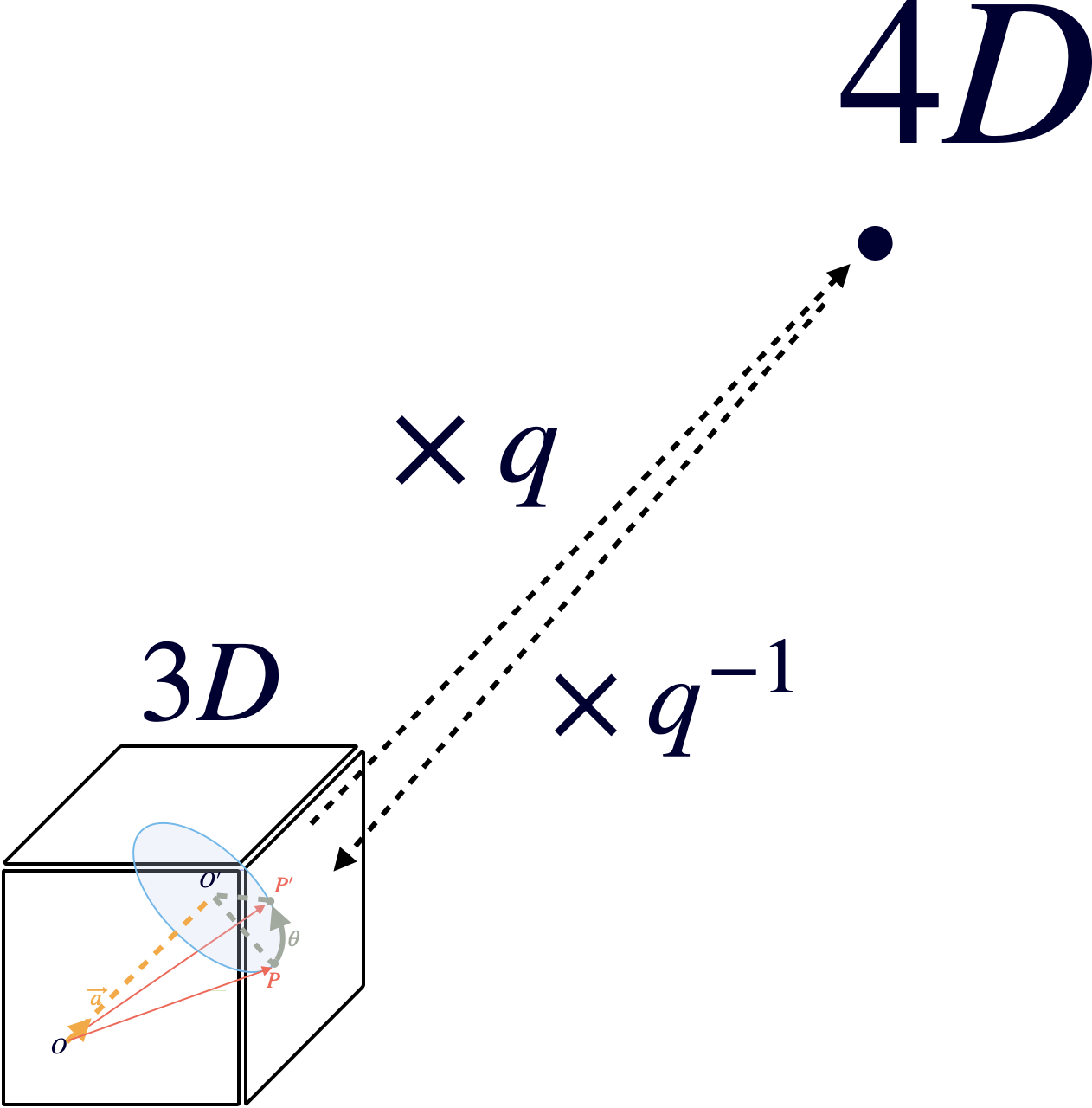
ロドリゲスの回転公式とクォータニオンの回転公式の違い
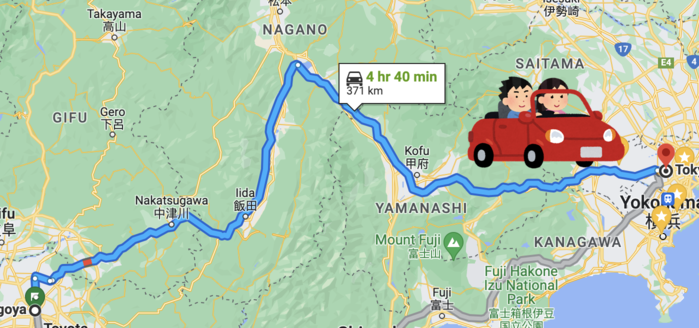
名古屋から東京に行くにあたって、
自家用車で行く場合は、曲がりくねった道を通る必要があります。
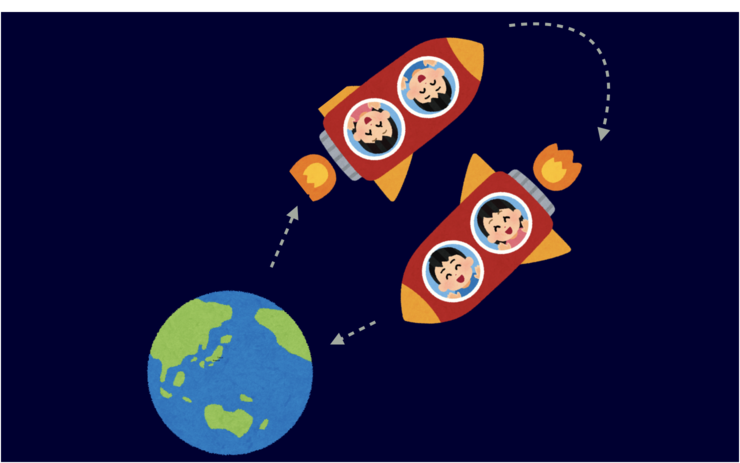
ですが自家用ロケットがあればどうでしょうか?
半分、宇宙空間を飛び、半分、宇宙空間から降りていければ、東京に行くことができるはずです。
3次元空間上の任意の頂点Pをある軸を中心に回転させるとき、ベクトル空間を使った回転を自家用車だとすれば、
クォータニオンを使った回転は、まさに自家用ロケットによる回転になります。
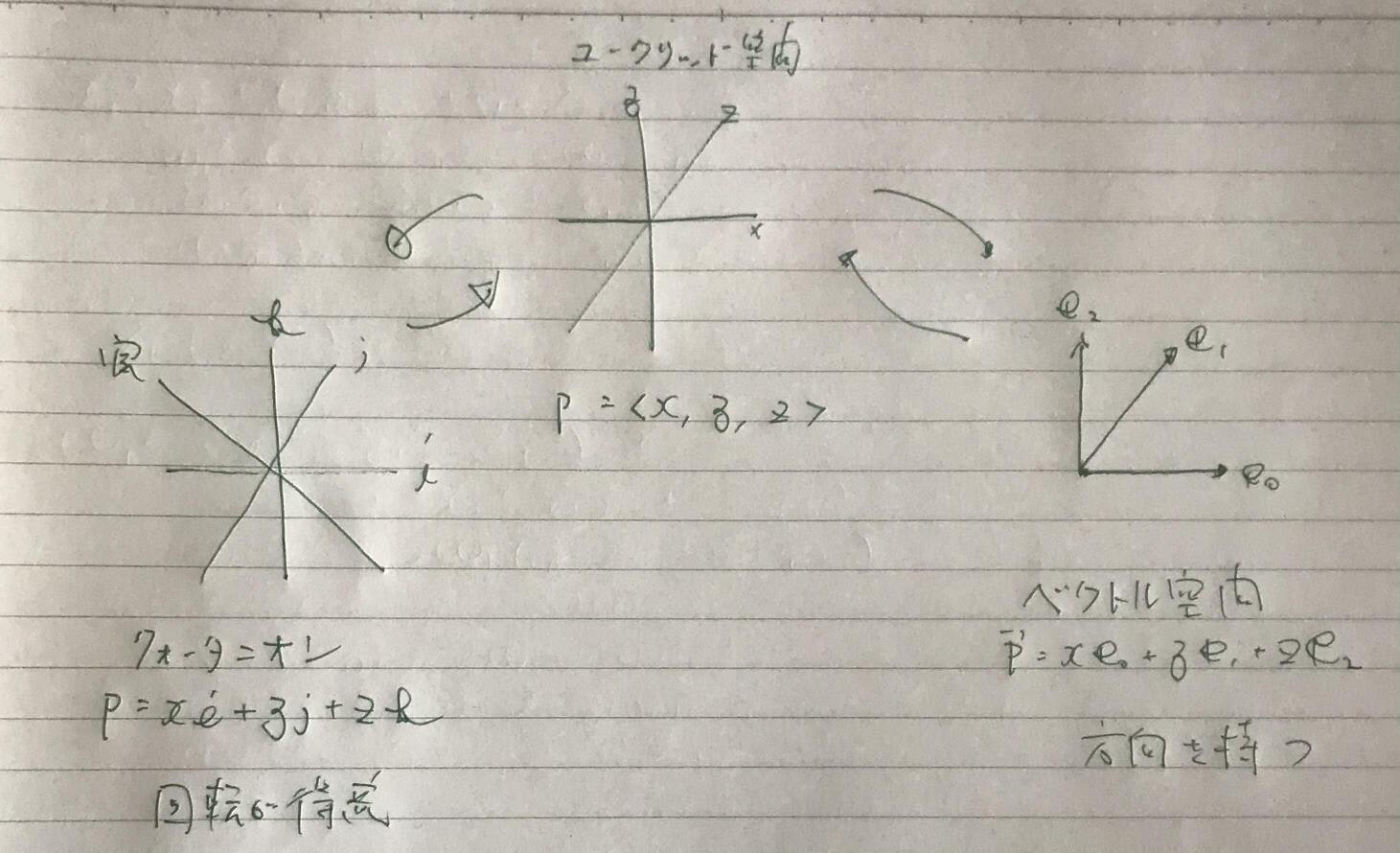
数式の表示について
- ベクトル - 矢印
- 純粋クォータニオン - 太字
例 頂点a$(x, y, z)$
| 数式 | |
|---|---|
| ベクトル | $\vec{a} = x\vec{e_x} + y\vec{e_y} + z\vec{e_z}$ |
| 純粋クォータニオン | $\mathbf{a} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ |
このように3次元空間の頂点を純粋クォータニオンで対応させることで、
ロドリゲスの回転公式からクォータニオンの回転公式が得られることを明らかにします。
3次元空間の回転
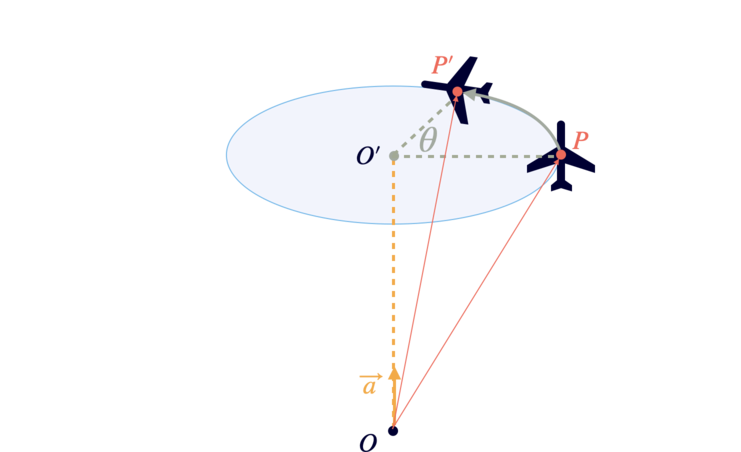
飛行機の旋回のように、ある物体(頂点P)をある任意の軸 $\vec{a}$ 周りに $\theta$ 回転させることについて考えます。
- 頂点P - 回転前の初期位置
- 頂点P' - 回転後の位置
回転公式
このときその公式として、以下の2つがあります。
- ロドリゲスの回転公式
- クォータニオンの回転公式
| ロドリゲスの回転公式 | クォータニオンの回転公式 | |
|---|---|---|
| 図 | 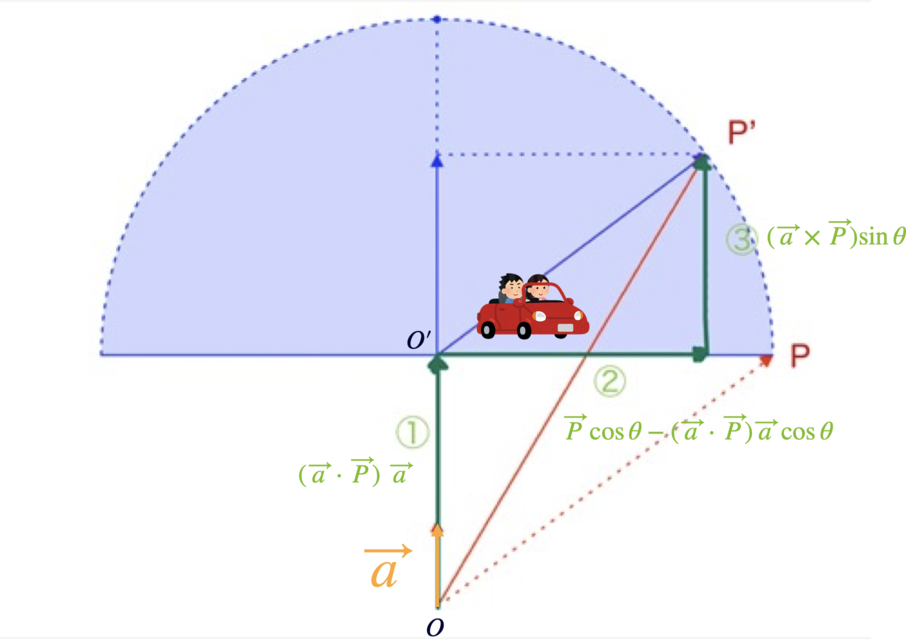 |
 |
| 舞台 | ベクトル空間 | クォータニオン |
| 次元 | 3次元 | 4次元 |
| 特徴 | * 頂点を表せる * 方向を表せる |
* 頂点を表せる * 回転を表せる |
ロドリゲスの回転公式
一般的にコンピュータービジョンで表される空間は、数ベクトル空間が使用されます。1
この空間をそのまま使って、任意の軸を中心に頂点を回転させる公式として、ロドリゲスの回転公式が使われます。
ロドリゲスの回転公式
\begin{multline}
\vec{P}' = \vec{a}\;(\vec{a}\cdot\vec{P}) + (\vec{P} - \vec{a}\;(\vec{a}\cdot\vec{P}))\cos\theta + (\vec{a} \times \vec{P})\sin\theta
\end{multline}
3つのベクトルの和で構成されており、この経路を図に表せば、どのように頂点P'を求めているか見ることができます。
クォータニオンの回転公式
クォータニオンは、複素数を使った複素平面と同じように、3次元空間上の頂点を回転させることができる代数が作れないかとという過程で考え出されたものです。
ウィリアム・ローワン・ハミルトンは、その代数を4次元に拡張することで、回転させる公式があることを発見したのです。
実はクォータニオンの回転公式は、ベクトル空間上のロドリゲスの回転公式をクォータニオンに変換し、こねくり回すことで、求めることが出来ます。
(従って必ず3次元の目的地P'にもどってくることが保証されます。)
では、それを早速見ていきましょう。
1. ロドリゲスの回転公式をクォータニオンに変換する
\mathbf{p}' = -\mathbf{a}\frac{\mathbf{ap} + \mathbf{pa}}{2} + (\mathbf{p} + \mathbf{a}\frac{\mathbf{ap} + \mathbf{pa}}{2})\cos\theta + \frac{\mathbf{ap} -\mathbf{pa}}{2}\sin\theta \tag{1}
上式の対応表
| ベクトル | クォータニオン | |
|---|---|---|
| ① | $\vec{a} (\vec{a}\cdot\vec{P})$ | $-\mathbf{a}\frac{\mathbf{ap} + \mathbf{pa}}{2}$ |
| ② | $(\vec{P} - \vec{a}(\vec{a}\cdot\vec{P}))\cos\theta$ | $(\mathbf{p} + \mathbf{a}\frac{\mathbf{ap} + \mathbf{pa}}{2})\cos\theta$ |
| ③ | $(\vec{A} \times \vec{P})\sin\theta$ | $\frac{\mathbf{ap} -\mathbf{pa}}{2}\sin\theta$ |
ベクトル空間からクォータニオンへの変換はこちらで詳解しています。
2. (1)式をこねくり回す
こねくり回すと
\begin{align}
\mathbf{p}' &= \mathbf{p}\cos\theta + \frac{\mathbf{ap} -\mathbf{pa}}{2}\sin\theta - \mathbf{a}\frac{\mathbf{ap} + \mathbf{pa}}{2}(1 - \cos\theta) \\
&= p\cos\theta + \frac{ap -pa}{2}\sin\theta - \frac{a(ap + pa)}{2}(1 - \cos\theta) \\
&= p\cos\theta + \frac{ap -pa}{2}\sin\theta - \frac{(aa)p + apa}{2}(1 - \cos\theta) \\
&= p\cos\theta + \frac{ap -pa}{2}\sin\theta + \frac{|a|^2p - apa}{2}(1 - \cos\theta) \\
&= p\cos\theta + \frac{ap -pa}{2}\sin\theta + \frac{p - apa}{2}(1 - \cos\theta) \\
&= p\frac{1 + \cos\theta}{2} + \frac{ap -pa}{2}\sin\theta - \frac{apa}{2}(1 - \cos\theta) \\
&= p\cos^2\frac{\theta}{2} + (ap - pa)\sin\frac{\theta}{2}\cos \frac{\theta}{2} -apa\sin^2\frac{\theta}{2} \\
&= \biggl( p\cos^2\frac{\theta}{2} + ap\sin\frac{\theta}{2}\cos\frac{\theta}{2} \biggr) - \biggl(pa\sin\frac{\theta}{2}\cos\frac{\theta}{2} + apa\sin^2\frac{\theta}{2}\biggr) \\
&= \Bigl(\cos\frac{\theta}{2} + a\sin\frac{\theta}{2}\Bigr) \Bigl(p\cos\frac{\theta}{2}\Bigr) - \Bigl(\cos\frac{\theta}{2} + a\sin\frac{\theta}{2}\Bigr) \Bigl(pa\sin\frac{\theta}{2}\Bigr) \\
&= \Bigl(\cos\frac{\theta}{2} + a\sin\frac{\theta}{2}\Bigr) \Bigl(p\cos\frac{\theta}{2} - pa\sin\frac{\theta}{2}\Bigr) \\
&= \Bigl(\cos\frac{\theta}{2} + a\sin\frac{\theta}{2} \Bigr) \; p \; \Bigl(\cos\frac{\theta}{2} - a\sin\frac{\theta}{2}\Bigr)
\end{align}
以下の式が得られる。
\mathbf{p'} = \Bigl(\cos\frac{\theta}{2} + \mathbf{a}\sin\frac{\theta}{2} \Bigr) \; \mathbf{p} \; \Bigl(\cos\frac{\theta}{2} - \mathbf{a}
\sin\frac{\theta}{2}\Bigr) \tag{2}
(2)式において、
\mathbf{q} = \cos\frac{\theta}{2} + \mathbf{a}\sin\frac{\theta}{2}
とおくことで、クォータニオンの回転公式が得られます。
\mathbf{p'} = \mathbf{q}\mathbf{p}\mathbf{q^{-1}} \tag{3}
(3)式において、頂点Pと頂点P'を表す$\mathbf{p}$, $\mathbf{p'}$ は、3次元空間上の頂点です。
一方、$\mathbf{qp}$, $\mathbf{pq^{-1}}$は、実数を含むため4次元空間上の頂点になります。
実際に$\mathbf{qp}$を計算すると実数wが現れる。
\begin{align}
\mathbf{qp} &= (\cos\frac{\theta}{2} + \mathbf{a}\sin\frac{\theta}{2}
)\mathbf{p} \\
&= \mathbf{p}\cos\frac{\theta}{2} + \mathbf{ap}\sin\frac{\theta}{2} \\
&= \mathbf{p}\cos\frac{\theta}{2} + (w + x\mathbf{i}+y\mathbf{j} + z\mathbf{k})\sin\frac{\theta}{2} \\
&= w\sin\theta + \mathbf{p}\cos\frac{\theta}{2} + \mathbf{p''}\sin\frac{\theta}{2}
\end{align}
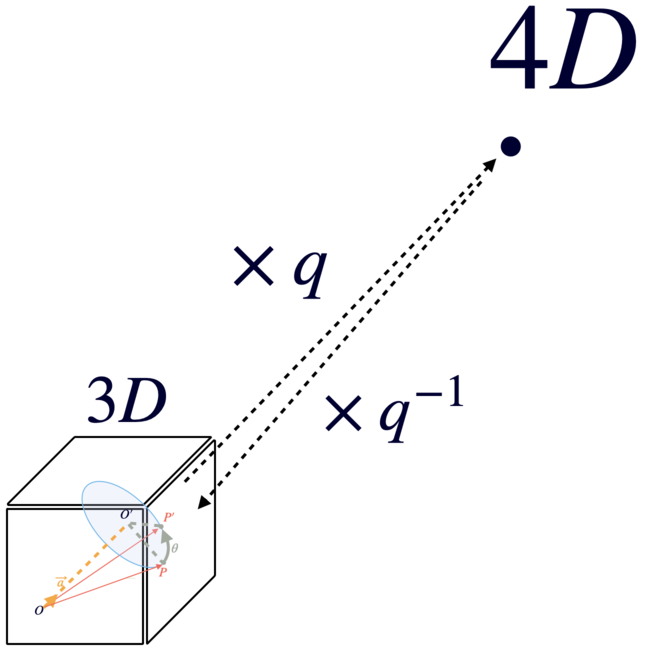
つまりハミルトンは、複素数を拡張した代数を使って3次元空間上の頂点を回転させるには、
4次元空間を通らなければならないことを発見したのです。
これは半分は4次元を飛び、半分は4次元から戻ってくるルートで回転しているといえます。
まさに$\frac{\theta}{2}$の正体でもある。
球面線形補間について
従ってクォータニオンは3次元上空を飛んでいく回転であるため、3Dでアニメーションを実現する際に困ってしまいます。
PからP'まで3次元空間に存在しないためです。
つまりクォータニオンの回転公式は、どこでもドアで、P'に移動することと同じ だと言えます。
これでは$\theta$をフレーム単位で割って、フレーム毎に4次元世界に飛んで戻ってを繰り返す必要があります。
そこで考案されたのが、球面線形補間です。
これは3次元空間上の話であるため、ロドリゲスの回転公式を使ってP'を求めた場合でも有効です。
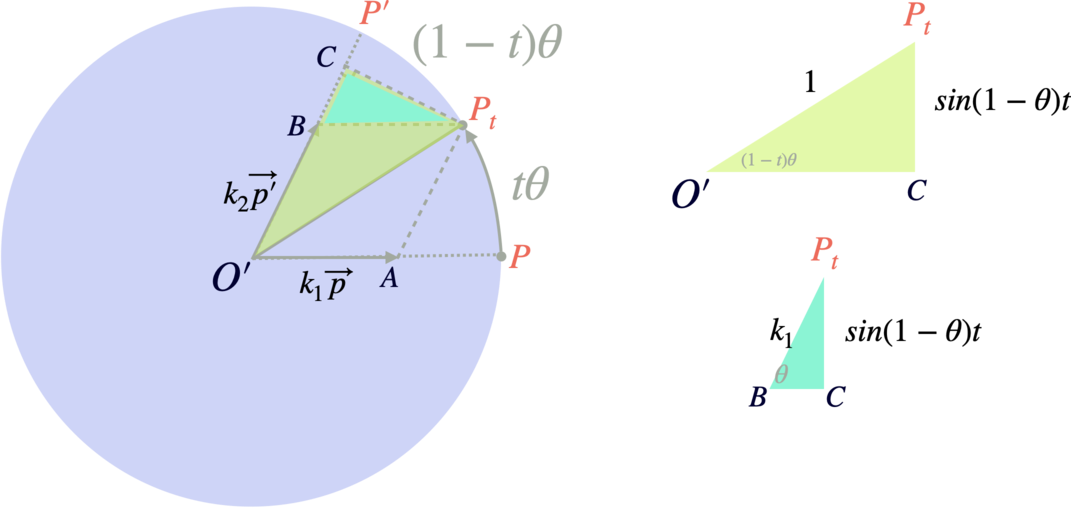
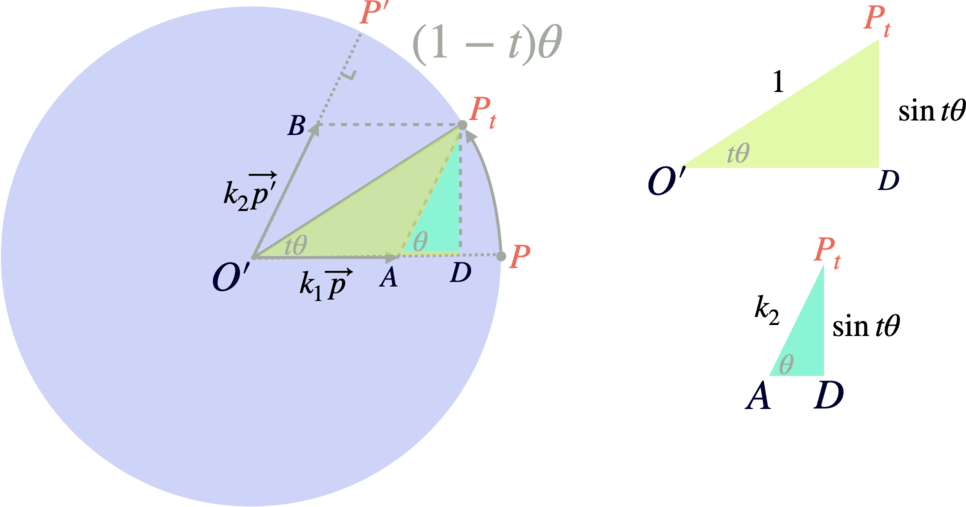
回転後の頂点P'を求め、ベクトル空間上において、頂点P,P'を結ぶ補間を表す頂点Ptを考えます。
このように頂点Ptは、ベクトルの和で表せます。
P_t = k_1\vec{P} + k_2\vec{P'} \tag{4}
さらに図から(4)式のk1, k2を $t\theta$ で表すことができれば 、頂点Ptは、孤PP'上の頂点であることが保証されます。
これは幾何学的に求めることが出来ます
\vec{P_t} = \frac{\sin(1-t)\theta}{\sin\theta}\vec{P} + \frac{\sin t\theta}{\sin\theta}\vec{P'}
まとめ
- クォータニオンの回転公式は、4次元を通る回転である
- クォータニオンは、4次元を通る回転であるため、その補間が必要となる。(球面線形補間)
参考書籍
-
正確に言うと、それを便宜的に拡張したアフィン空間ですが、拡張部分は回転とは無関係です ↩