TL;DR
- 「集合」は「条件」を可視化したもの
- 「条件」とは、「変数を含む命題」
集合
ある条件を満たすものの集まりであり、二通りの記法がある
- 外延的記法 - 要素をすべて並べる
- 内包的記法 - 要素を満たす条件を指定する
外延的記法
\{..., -4, -2, 0, 2, 4, 8, ... \}
\{1,3,5,7\}
内包的記法
\{2n\,|\,nは整数 \}
\{2x-1 \,|\, xは整数かつ1\leqq x \leqq 4\}
$\hookrightarrow$ 内包的記法を使うことで、集合は「条件」を使って表すことができる。
条件
数学的における条件とは、「変数を含む命題」である
- 「変数」とは、任意の値を代入することができる文字のことである
- 「命題」とは、真偽を問うことが出来る式や文章のことである
例として「富士山は日本一高い山である」は、真偽を問うことが出来るので命題であるが、「タモリは面白い」は真偽が曖昧なため命題ではない。
つまり「条件」とは、
「文字が含まれ、値を代入することで真偽を問うことが出来る式や文章」
であると言える。
例として、「$2x - 5 > 0$」は、値を代入することで真偽を問うこと出来るので命題となり、変数を含むので「条件」となる。
2つの条件の関係
仮定と結論
2つの条件p, qを使って、
**「pならばqである」**と表現できる命題を
p \Rightarrow q
と表せる。
このときpを仮定、qを結論という。
十分条件と必要条件
「pならばqである」という命題において、
p \Rightarrow q \,が真である
- pはqの十分条件
- qはpの必要条件
という。
またその逆「qならばpである」が同様に真であるならば、
p \Leftrightarrow q \,が真である
と表わせ、pとqは互いに必要十分条件という。
2つの条件の関係と集合
集合を使うことで、条件が互いにどういう関係になっているのかを可視化することができる。
全体集合を$U$とし、集合の要素のうち、
\left\{
\begin{array}{ll}
条件pを満たす集合をP \\
条件qを満たす集合をQ
\end{array}
\right.
とする。
- $p \Rightarrow q ,が真である ;\Leftrightarrow; P \subset Q$
- $p \Leftrightarrow q ,が真である ;\Leftrightarrow; P = Q$
が言える。
Appendix
集合
要素の個数による集合の種類
- 有限集合 - 要素の個数が有限
- 無限集合 - 要素の個数が無限
全体集合は無限集合であることが多い (整数、実数、無理数)
2つの集合の包含関係
- 2つの集合AとBにおいて、AはBの部分集合
A \subset B
- 2つの集合AとBにおいて、要素が同一、AとBは等しい
A = B
- 2つの集合AとBにおいて、AはBの部分集合であるが、等しくなければ、AはBの真部分集合
A \subsetneq B
全体集合・部分集合・補集合・空集合
全体集合・部分集合
集合を考えるとき、ある集合 $\mathbb U$を固定し、その要素や部分集合を考える。
このとき、$\mathbb U$を全体集合という。
全体集合の例
- 素数について考えるとき、$\mathbb N$(自然数)を全体集合とする
- 有理数・無理数について考えるとき、$\mathbb R$(実数)を全体集合とする
$\hookrightarrow$ 全体集合は、無限集合であることが一般的
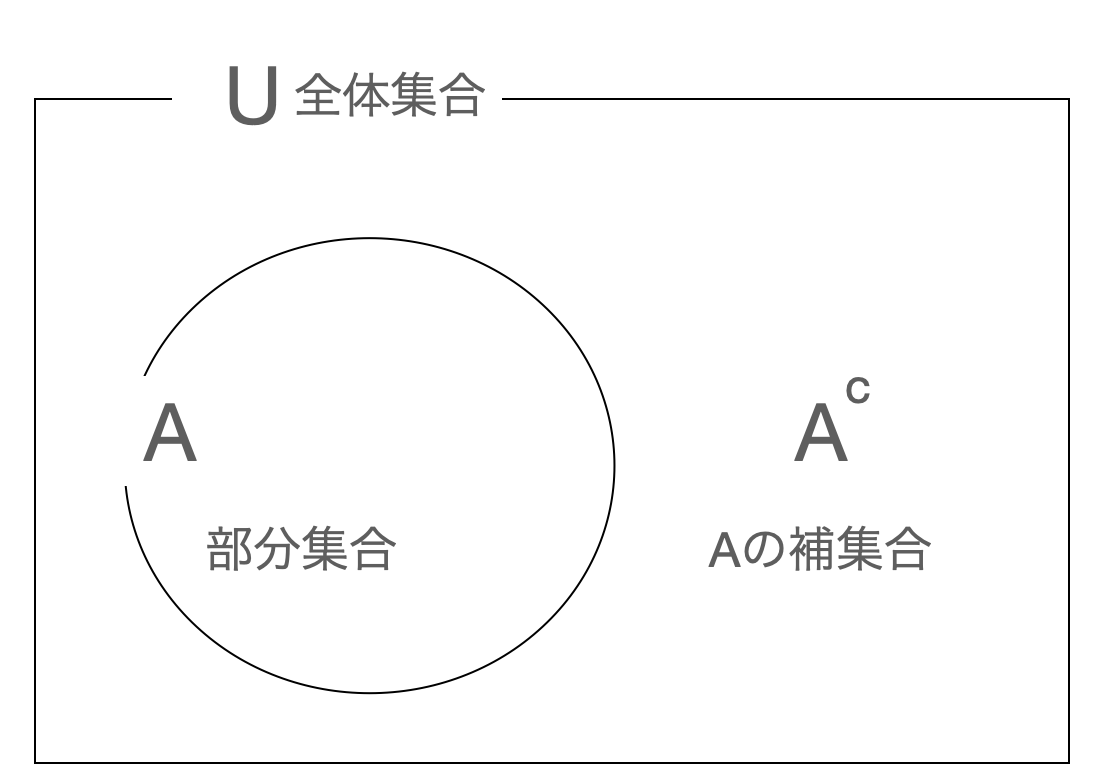
補集合
全体集合Uの部分集合Aに対して、Aに属さない全てのそうその集合をAの補集合といい、以下のように表す。
\mathbb A^c \;もしくは\; \overline{\mathbb A}
空集合
要素を持たない集合を空集合 ($\emptyset$) といい、全ての集合の部分集合である。
全体集合を $\mathbb U$とすると、以下を満たす
- $\emptyset = \mathbb U$
- $\emptyset = \overline{\mathbb U}$