はじめに
『機械学習のエッセンス(http://isbn.sbcr.jp/93965/)』のPythonサンプルをJuliaで書き換えてみる。(第04章06乱数)の続きです。
前提・準備
ここではJuliaのパッケージPlotsを使います。
本の第02章に書かれているのと同様、なるべくファイル実行とREPLで試しているのでJupyter Notebookは使用していません。
※環境等については一番最後に補足で書きました。
Plotsパッケージのインストール
julia> using Pkg
julia> Pkg.add("Plots")
しばらく時間がかかります。
Plotsパッケージの確認
次の関数が表示できるか確認します。
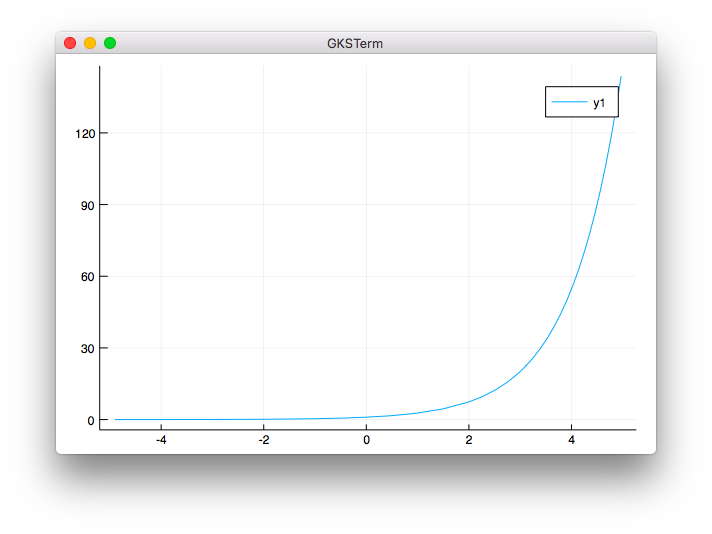
f(x) = exp(x)
julia> using Plots
julia> f(x) = exp(x)
f (generic function with 1 method)
julia> plot(f)
下記のように表示されれば、以降のサンプルは確認できるはずです。
デフォルトではGRというパッケージで描画するようです。
https://docs.juliaplots.org/latest/examples/gr/
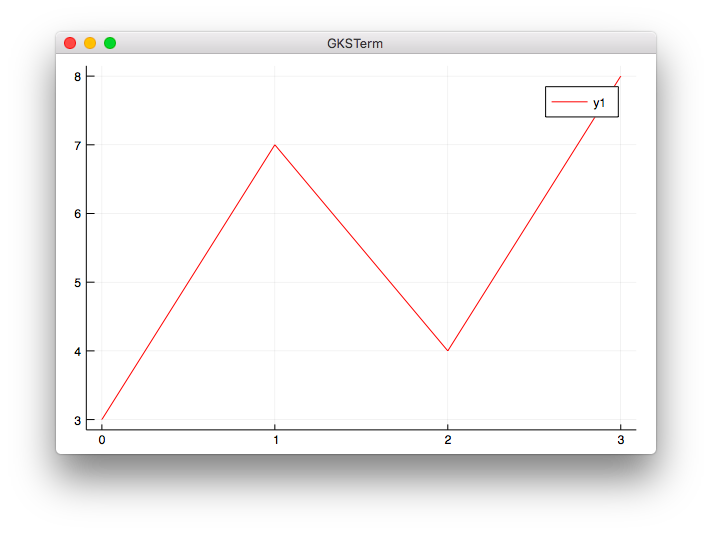
折れ線グラフ
using Plots
x = [0, 1, 2, 3]
y = [3, 7, 4, 8]
plot(x, y, color="red")
実行結果
julia> include("plot1.jl")
ラベルy1が表示されていますが気にしないで進めます。
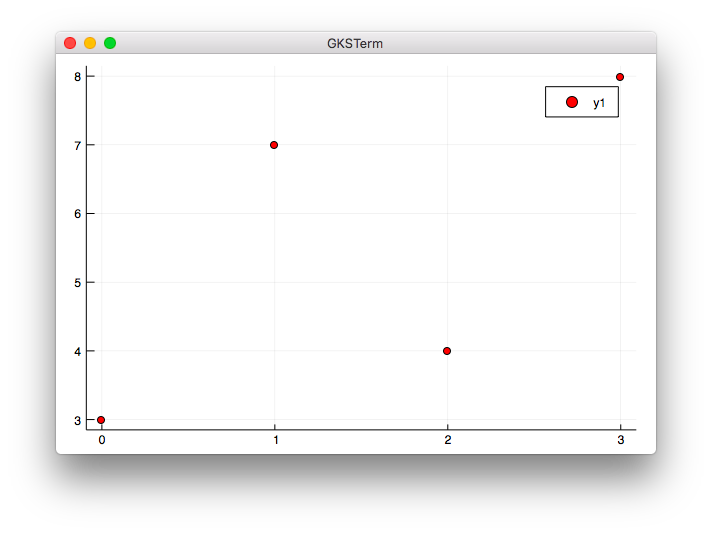
散布図
using Plots
x = [0, 1, 2, 3]
y = [3, 7, 4, 8]
scatter(x, y, color="red")
実行結果
julia> include("scatter1.jl")
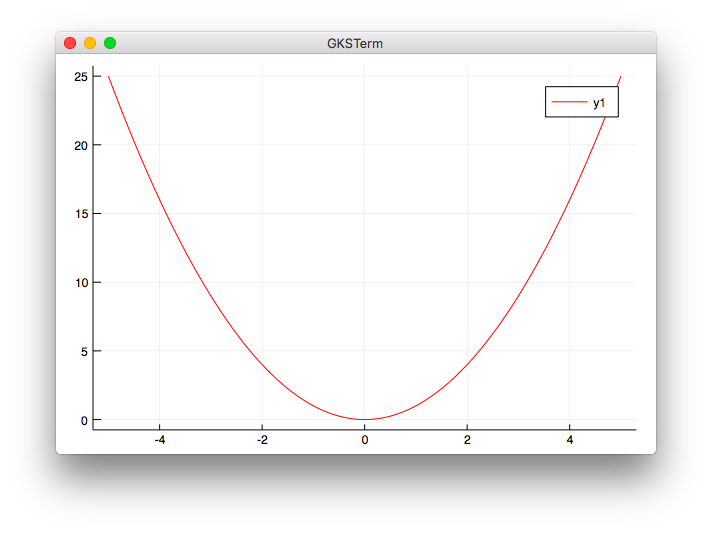
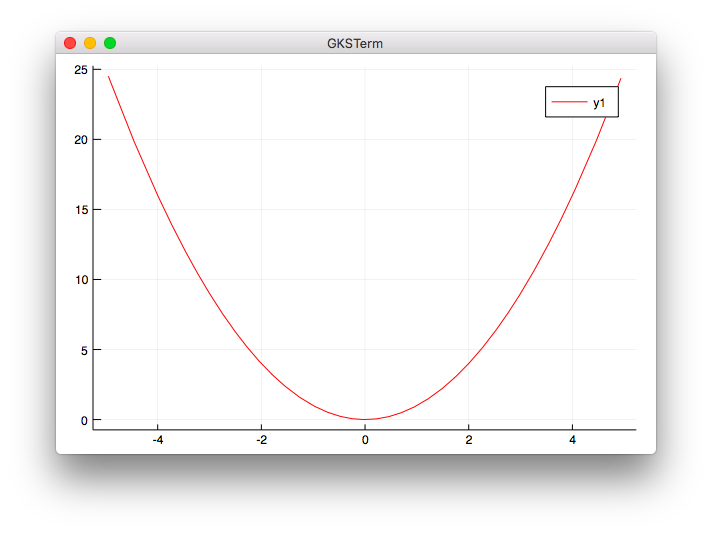
曲線のグラフ
y = x^2
Juliaでグラフについて調べたところ曲線は(数式風に記載した)関数そのものを指定すれば描画できるようです。(パッケージインストール確認の$f(x) = exp(x)$が例です)。Pythonで区間の点を多数取っているのはそれができないのでしょうか。あるいは、もしかしたら機械学習では大量のデータから曲線を描画することがあるのかもしれないので、本と同じ「点から描画する方法」と、「(数式風)関数でそのまま描画する方法」の2通りで書いてみました。
- 点から描画する
using Plots
x = collect(LinRange(-5, 5, 300))
y = x.^2
plot(x, y, color="red")
- 関数指定
using Plots
f(x) = x^2
plot(f, color="red")
実行結果
julia> include("plot2-1.jl")
julia> include("plot2-2.jl")
参考
@timeを付けると実行時間を計れるので2つを比較してみました。
julia> @time include("plot2-1.jl")
0.003481 seconds (2.66 k allocations: 201.438 KiB)
julia> @time include("plot2-2.jl")
0.523554 seconds (578.27 k allocations: 28.183 MiB, 1.45% gc time)
詳しいメッセージがわからないので断定は出来ませんが、上記の2通りなら点から描画する方が早いようです。
以降は関数指定の方法だけにします。
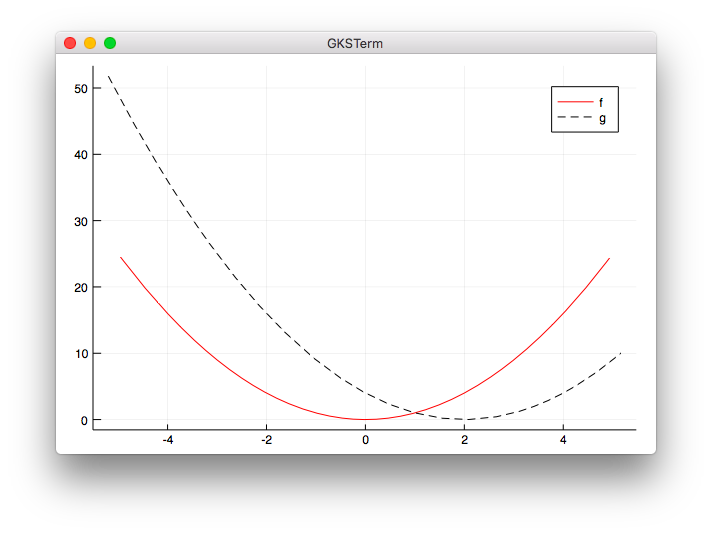
複数の線を表示する
using Plots
f(x) = x^2
g(x) = (x-2)^2
plot(f, color="red", label="f")
plot!(g, color="black", linestyle=:dash, label="g")
-
plotに続けてplot!を指定することで元のグラフに追加できました。 -
plotの引数にlinestyleを指定すると線の形式が変更できました。次の種類があります。:auto, :solid, :dash, :dot, :dashdot, :dashdotdot
実行結果
julia> include("plot3.jl")
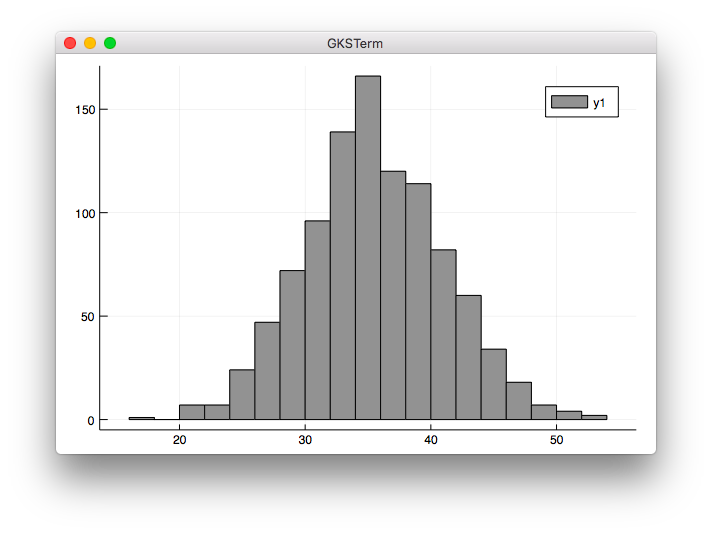
ヒストグラム
using Plots
using Random
Random.seed!(0)
l = []
for i in 1:1000
append!(l, sum(rand(1:6, 10)))
end
histogram(l, bins=20, color="gray")
ビンの指定は下記を参照しました。
https://docs.juliaplots.org/latest/attributes/
実行結果
julia> include("hist1.jl")
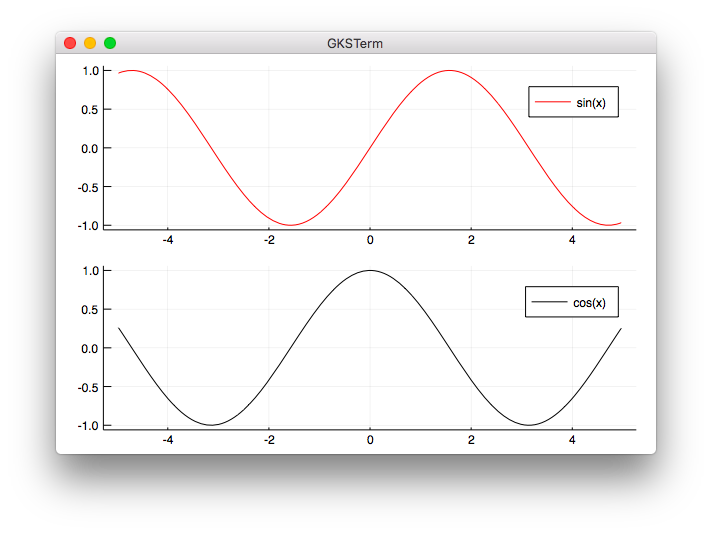
複数のグラフを並べて表示する
2つのplotとlayoutを指定することで並べて表示することが出来ました。
using Plots
f(x) = sin(x)
g(x) = cos(x)
p1 = plot(f, color="red", label="sin(x)")
p2 = plot(g, color="black", label="cos(x)")
plot(p1, p2, layout=(2,1))
実行結果
julia> include("subplot1.jl")
- 本の
subplots2.pyはMatplotlibの説明なので省略します。
等高線の描画
x^2 + \frac{y^2}{4} = k
楕円の方程式をyについて解くと、
y = \pm2\sqrt{k - x^2}
となって一意に定まらないため数学での関数にならず、今まで通りのJuliaの数式風関数指定ではうまくいきません。
試しに、$\pm$を使って定義してみました。
- $k = 1$のとき
julia> f(x) = ±2sqrt(1 - x^2)
ERROR: syntax: "±" is not a unary operator
当然ですがエラーになります。
そのため、本に記載されているようにmashgridを使う方法を調べたところ下記の黒木玄さんのTweetを見つけました。
#Julia言語 しかし、
— 黒木玄 Gen Kuroki (@genkuroki) 2018年4月9日
z = f.(x_grid, y_grid)
と
z = f.(x',y)
は同じ結果になるので、x,yの要素の組にfを作用させて行列を作りたいなら、meshgridは必要ありません。
meshgridを流行らせた人達は無駄で効率が悪いものを流行らせて技術社会に負の貢献をしたと評価されるべきだと思います。
※私がJuliaという言語を知ったのも黒木さんのTweetでした。
ということで、z = f.(x',y)の記述をもとに作成してみました。
等高線はcontourという関数がありました。
using Plots
f(x, y) = x^2 + y^2 / 4
x = LinRange(-5, 5, 300)
y = LinRange(-5, 5, 300)
z = f.(x', y)
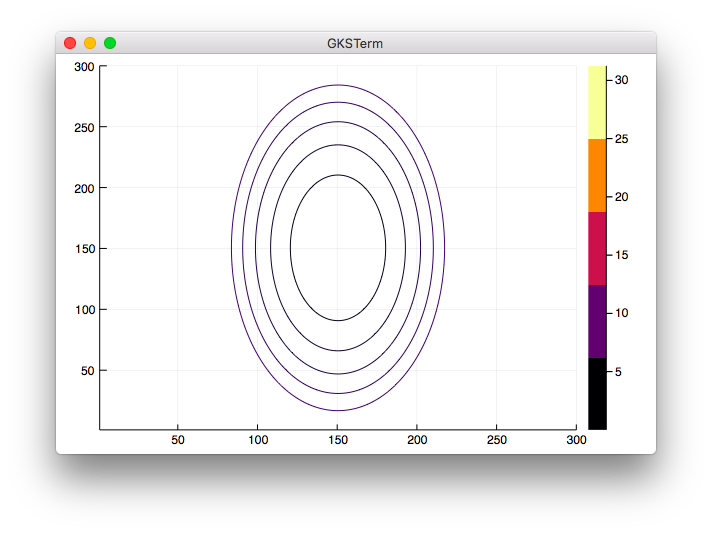
contour(z, levels=[1,2,3,4,5])
実行結果
julia> include("contour1.jl")
うまく表示できました。
が、目盛がPythonの場合とだいぶ違います。これはJuliaのPlotの特徴でしょうか。LinRangeで指定する数値をいろいろ変えてみましたが、本と似たような目盛にはできませんでした。一旦、このまま進めます。
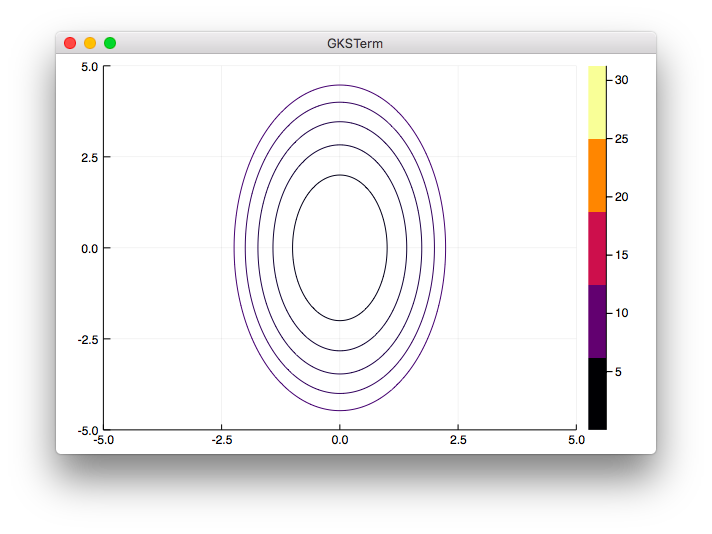
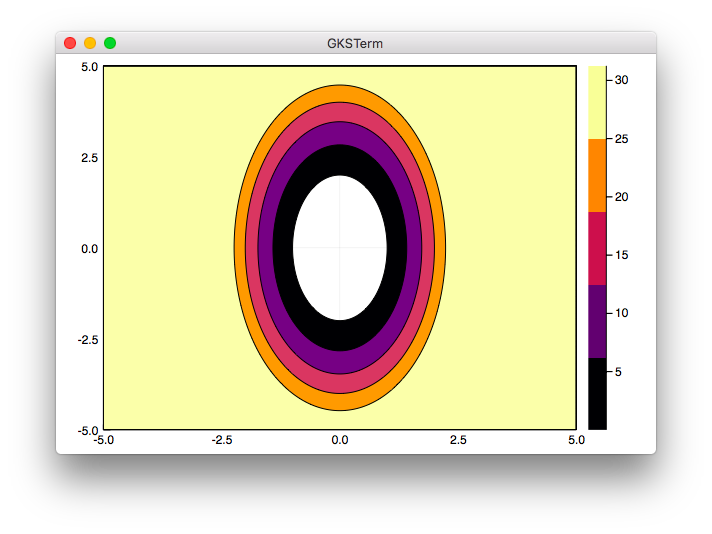
(追記) contour 関数の最初の引数にxとyを入れたところ-5〜5で表示が出来ました。
using Plots
f(x, y) = x^2 + y^2 / 4
x = LinRange(-5, 5, 300)
y = LinRange(-5, 5, 300)
z = f.(x', y)
contour(x, y, z, levels=[1,2,3,4,5])
julia> include("contour1_1.jl")
- f.(x', y)の動きを確認
本ではmeshgridについて詳しく書かれているので、ここではf.(x', y)を確認してみます。
julia> x = [1, 2, 3]
3-element Array{Int64,1}:
1
2
3
julia> y = [4, 5, 6]
3-element Array{Int64,1}:
4
5
6
julia> x1 = x'
1×3 LinearAlgebra.Adjoint{Int64,Array{Int64,1}}:
1 2 3
julia> f(x, y) = x * y
f (generic function with 2 methods)
julia> x' .* y
3×3 Array{Int64,2}:
4 8 12
5 10 15
6 12 18
julia> f.(x', y)
3×3 Array{Int64,2}:
4 8 12
5 10 15
6 12 18
xとyは配列なので、定義したときは3 x 1の配列で、x'は転置なので1 x 3の配列ですが、それをfに.付き、つまりブロードキャストで渡すと3 x 3になりました。
(なんだか不思議です。まだブロードキャストをよく理解できていないようです。)
$f(x, y) = x^2 + y^2 / 4$でも試してみます。
julia> x = [1, 2, 3]
3-element Array{Int64,1}:
1
2
3
julia> y = [4, 5, 6]
3-element Array{Int64,1}:
4
5
6
julia> f(x, y) = x^2 + y^2 / 4
f (generic function with 2 methods)
julia> f.(x', y)
3×3 Array{Float64,2}:
5.0 8.0 13.0
7.25 10.25 15.25
10.0 13.0 18.0
- 領域の塗り分け
領域を塗る等高線はPythonと同様contourfという関数がありました。
が・・・、色の指定が全然うまくいかず、いろいろ数値を変えたり調べたりしましたが、グラデーションがかかったようなはっきりしない色しか出来ませんでした。
(追記)これも上記と同じく、目盛表示を-5〜5にしたらうまく表示できました。
using Plots
f(x, y) = x^2 + y^2 / 4
x = LinRange(-5, 5, 300)
y = LinRange(-5, 5, 300)
z = f.(x', y)
colors = [0.1, 0.3, 0.5, 0.7]
levels = [1, 2, 3, 4, 5]
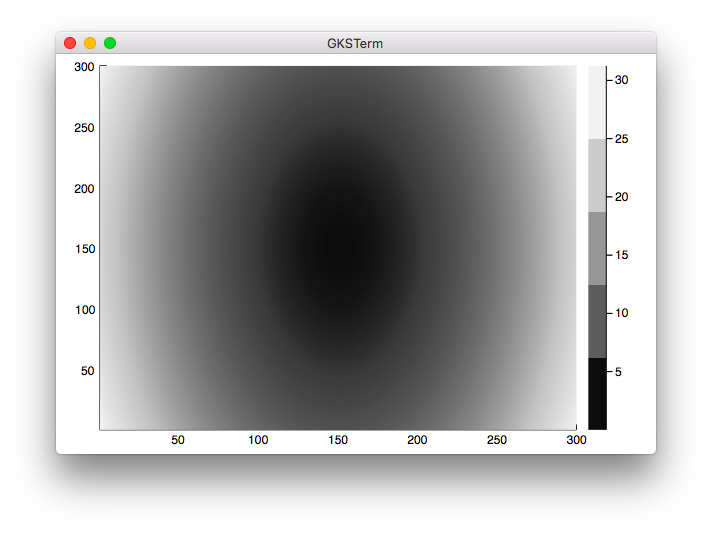
contourf(z, fill=(true,cgrad(:grays,colors)), levels=levels)
実行結果
julia> include("contour2.jl")
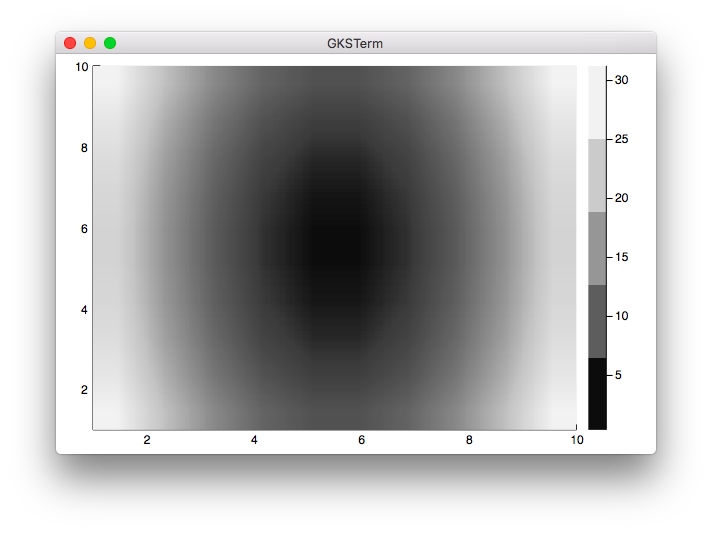
- グレーで指定した場合
なんだか境界線がよくわからないですね。
(目盛表示を変更したらうまくいきました。追記してあります。)
- (追記)目盛を変更した場合
using Plots
f(x, y) = x^2 + y^2 / 4
x = LinRange(-5, 5, 300)
y = LinRange(-5, 5, 300)
z = f.(x', y)
colors = [0.1, 0.3, 0.5, 0.7]
levels = [1, 2, 3, 4, 5]
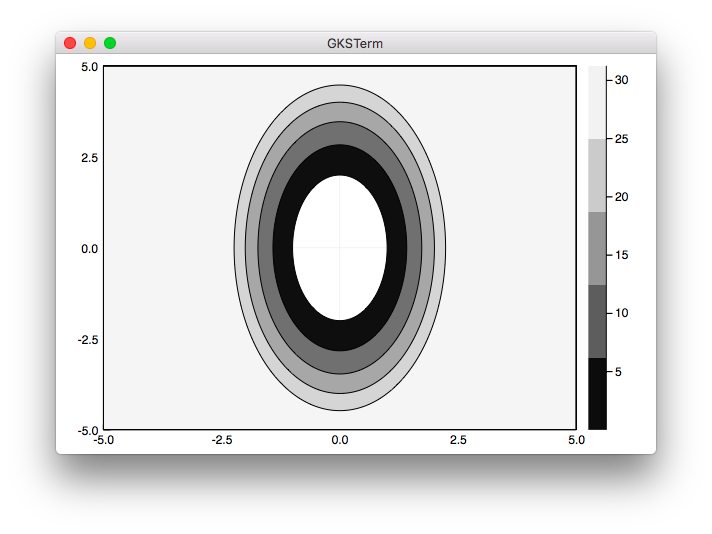
contourf(x, y, z, fill=(true,cgrad(:grays,colors)), levels=levels)
julia> include("contour2_1.jl")
- 色を指定しないデフォルトの場合
contourfの部分を下記のようにした場合です。
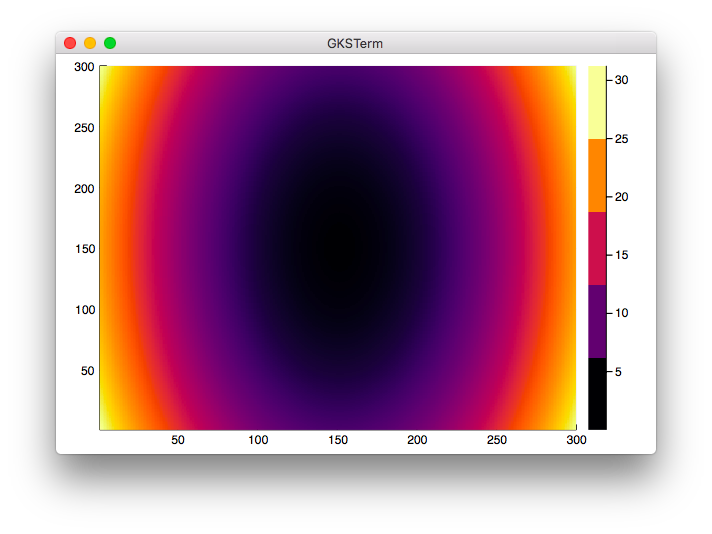
contourf(z, levels=levels)
色は派手ですが、やはり境界線がはっきりせずグラデーションになっています。
(追記)目盛を変えたらこちらもうまくいきました。追記してあります。
- (追記)目盛を変更した場合
はっきりときれいな色分けができています。
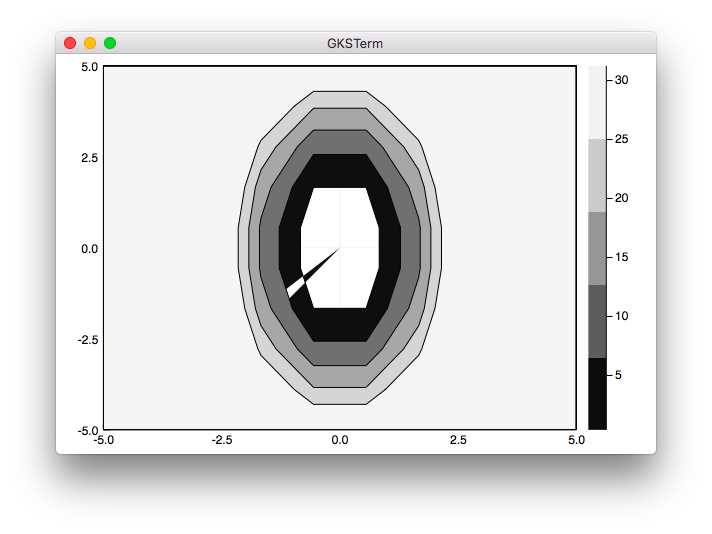
- メッシュを荒くした場合
ためしに、下記のように点を荒くして試してみました。
x = LinRange(-5, 5, 10)
y = LinRange(-5, 5, 10)
全然ダメですね。
(追記)こちらも試しに目盛を修正してみました。色はきれいですが一部変な形になりました。
塗り分けについては一旦保留することにします。
(追記)目盛の変更の仕方がわかったので上記に追記してあります。
補足
-
サンプルを確認した環境はMacです。
-
Windows10でもJuliaの
.exeでインストールしたものでは、セキュリティの警告が出ますが、許可すると表示されました。 -
bash on ubuntu on windowsにJuliaをインストール(.tar.gzを展開)したものはエラーが出て表示されませんでした。(解決方法については調べていません。) -
GRでない別のパッケージを入れた後、下記のエラーが出て描画が出来なくなりました。
ERROR: error compiling _plot!: error compiling _display: could not load library "libGR.so"
dlopen(libGR.so.dylib, 1): image not found
下記で解決しました。
julia> ENV["GRDIR"]=""
julia> using Pkg
julia> Pkg.build("GR")