『機械学習のエッセンス(http://isbn.sbcr.jp/93965/)』のPythonサンプルをJuliaで書き換えてみる。（第05章03リッジ回帰）

はじめに

『機械学習のエッセンス(http://isbn.sbcr.jp/93965/)』のPythonサンプルをJuliaで書き換えてみる。（第05章02回帰）の続きです。

記号の説明

前回の特徴量ベクトルが多次元の場合の記号の説明をもう一度記載しておきます。

y = w_0 + w_1x_1 + w_2x_2 + \cdots w_dx_d + \varepsilon

$(x_0,\cdots,x_d)^T$は入力変数、$w_0, w_1, \cdots, w_d$はパラメータ、$y$はターゲット、$\varepsilon$はノイズ。

ベクトル$x=(x_1,x_2,\cdots,x_d)^T$に対して要素1を付加したベクトル$\tilde{x}$、ベクトル$w=(w_0,w_1,\cdots,w_d)^T$とすると、

y = w^T\tilde{x}

行列$X$について、左に1列追加してその要素をすべて１としたものを$\tilde{X}$とする。

\hat{y}(w) = \tilde{X}w 

リッジ回帰

リッジ回帰はパラメータ$\lambda$を追加して、

E(w) = ||y - \hat{y}(w)||^2 + \lambda||w||^2

を最小化する$w$を決定する。

途中計算は省略します。

w = (\tilde{X}^T\tilde{X} + \lambda I)^{-1}\tilde{X}^Ty

$\lambda$はハイパーパラメータと呼ばれる。

ridge.jl

module ridge
using LinearAlgebra

mutable struct RidgeRegression
  λ_
  w_
  function RidgeRegression(lambda=1.)
    new(lambda, Nothing)
  end
end

function fit(s::RidgeRegression, X, t)
  Xtil = hcat(ones(size(X)[1]), X)
  c =  Matrix{Float64}(I, size(Xtil)[2], size(Xtil)[2]) # 単位行列
  A = Xtil' * Xtil + s.λ_ * c
  b = Xtil' * t
  s.w_ = A \ b
end

function predict(s::RidgeRegression, X)
  Xtil = hcat(ones(size(X)[1]), X)
  return Xtil * s.w_
end

end

次のridge_test1.jlは、本では2つの図を表示するプログラムになっていて、1つめが表示された後に、その画面を閉じるともう一つの図が表示されるようになっていますが、同じように書いたところ後半の図だけが表示されてしまいました。そのため前半の図をridge_test1.jl、後半の図をridge_test1_2.jlに分けました。

ridge_test1.jl

using .ridge
using Plots

x = [1, 2, 4, 6, 7]
y = [1, 3, 3, 5, 4]

model = ridge.RidgeRegression(1.)
ridge.fit(model, x, y)
b, a = model.w_

scatter(x, y, color="black")
xmax = maximum(x)
plot!([0, xmax], [b, b + a * xmax], color="black")

ridge_test1_2.jl

using .ridge
using Random
using Plots

n = 100
scale = 10
Random.seed!(0)
X = rand(n, 2) .* scale
w0 = 1
w1 = 2
w2 = 3
y = w0 .+ w1 * X[:, 1] .+ w2 * X[:, 2] .+ randn(n)

model = ridge.RidgeRegression()
ridge.fit(model, X, y)

x_range = LinRange(0, scale, 20)
y_range = LinRange(0, scale, 20)
xmesh = repeat(x_range', outer=(length(y_range),1))
ymesh = repeat(y_range,  outer=(1,length(x_range)))
zmesh = reshape(model.w_[1] .+ model.w_[2] .* vec(xmesh) .+ model.w_[3] .* vec(ymesh), size(xmesh))

plot(x_range, y_range, zmesh, color="red", st=:wireframe)
scatter!(X[:,1], X[:,2], y, color="black")

実行結果

julia> include("ridge.jl")
Main.ridge

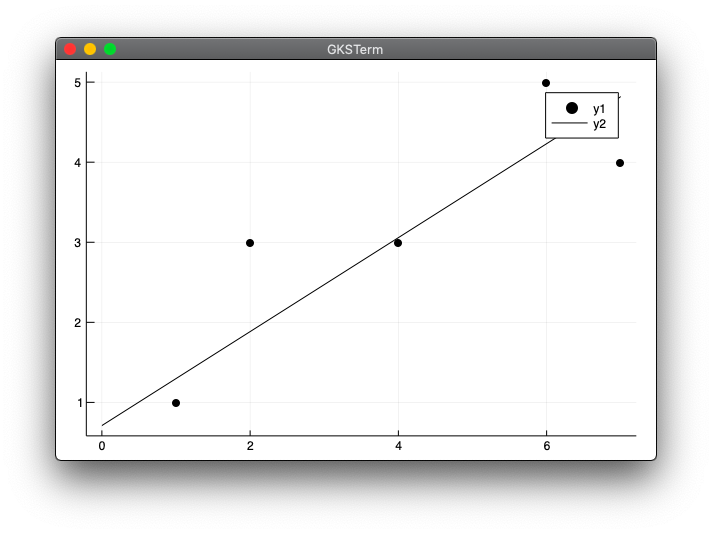
julia> include("ridge_test1.jl")

続けて次を実行します。

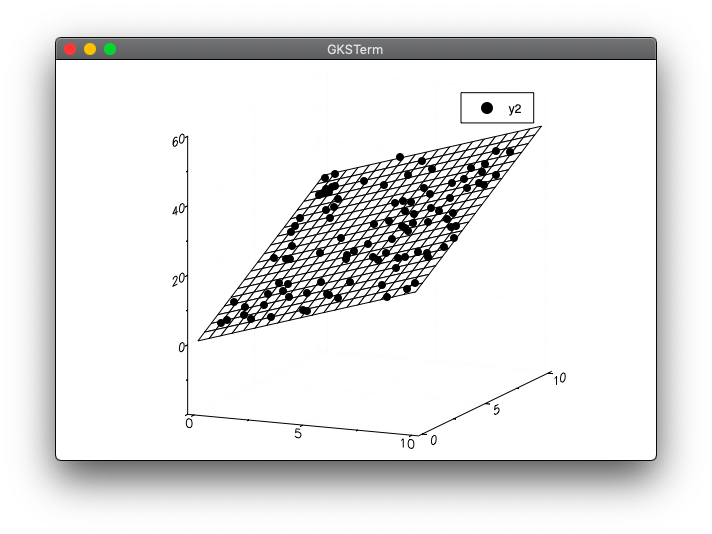
julia> include("ridge_test1_2.jl")

違う実験

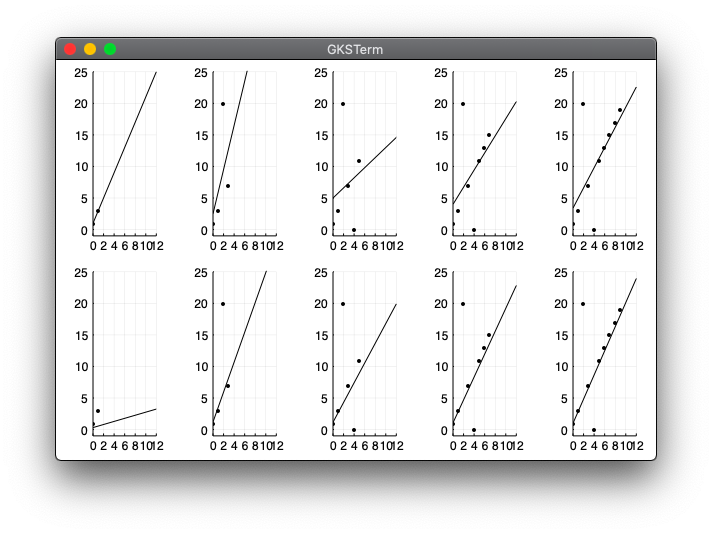
ほぼ線形に並んでいる点列を使うが、2つだけ大きくずれた値になるように人工データを用意。
12個のデータに対して2個からスタートして2個ずつ増やして回帰の様子がどうなるかを図示。

ridge_test2.jl

using .ridge
using .linearreg
using Plots

x = collect(0:11)
y = 1 .+ 2 .* x
y[3] = 20
y[5] = 0

xmin = 0
xmax = 12
ymin = -1
ymax = 25

plt_l = []
plt_r = []

for i in 0:4
    xx = x[1:(2 + i * 2)]
    yy = y[1:(2 + i * 2)]
    plt_s1= scatter(xx, yy, color="black", markersize = 2,
                    xlim=(xmin, xmax), ylim=(ymin, ymax), label="")

    model = linearreg.LinearRegression()
    linearreg.fit(model, xx, yy)
    xs = [xmin, xmax]
    ys = [model.w_[1] + model.w_[2] * xmin,
    model.w_[1] + model.w_[2] * xmax]

    push!(plt_l,plot!(plt_s1, xs, ys, color="black", label=""))

    model = ridge.RidgeRegression(10.)
    ridge.fit(model, xx,yy)
    xs = [xmin, xmax]
    ys = [model.w_[1] + model.w_[2] * xmin,
    model.w_[1] + model.w_[2] * xmax]

    plt_s2 = scatter(xx, yy, color="black", markersize = 2,
                     xlim=(xmin, xmax), ylim=(ymin, ymax), label="")
    push!(plt_r, plot!(plt_s2, xs, ys, color="black", label=""))

end

plot(plt_l[1], plt_l[2], plt_l[3], plt_l[4], plt_l[5],
     plt_r[1], plt_r[2], plt_r[3], plt_r[4], plt_r[5],
     layout=(2,5))

実行結果

実行には前回のlinearreg.jlが必要です。

julia> include("linearreg.jl")
Main.linearreg

julia> include("ridge.jl")
Main.ridge

julia> include("ridge_test2.jl")