目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義 |
| tree.py | ゲーム木に関する Node、Mbtree クラスなどの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
置換表に登録された最善手のバグの修正
前回の記事では 反復深化を利用した move ordering について説明し、move ordering を行うために 必要なデータを置換表に記録する処理を実装 しましたが、置換表に登録された最善手が間違っているというバグがある ことが判明しましたので、最初にそのバグの原因の検証と修正を行います。
なお、前回の記事で説明したように、本記事では move ordering の文脈 では 最善手 という用語が refutation move1 を含む ことにします。また、ゲーム木の探索 で各 ノードに対して計算される値 の事を一般的に使われている 評価値と表記 することにします。
バグの原因の検証
置換表に登録された 最善手が間違っている ので、ai_abs_dls 内の下記の置換表に 最善手を登録する処理 を行うプログラムを 検証する ことにします。
この中で問題となるのは 10、11 行目 の処理で、この処理では 2 行目で計算した mborig の同一局面に対して同一の合法手 を最善手として登録しています。
1 if use_tt:
2 boardtxtlist = calc_same_boardtexts(mborig)
3 if score <= alphaorig:
4 upper_bound = score
5 elif score < betaorig:
6 lower_bound = score
7 upper_bound = score
8 else:
9 lower_bound = score
10 for boardtxt in boardtxtlist:
11 tt[boardtxt] = (lower_bound, upper_bound)
同一局面 は、以前の記事で説明したように、元の局面に対して 7 種類の回転や反転などの操作 を行った局面です。下図の下の行に表示される 8 つの局面は同一局面です。これらの同一局面を 左から順番に 1 ~ 8 の数字を割り当てて番号で表記 することにします。
2 ~ 4 番の局面 は 1 番の局面を 90 度、180 度、270 度 回転させた局面 で、5 ~ 8 番の局面 は上の段に表示されている線で 反転させた局面 です。

図の 上段の図のマスの中の数字 は、同一局面の 対応するマス を表しています。例えば 1 番の局面の (1, 2) のマスは上の段では 8 が表記されている ので 2 番の局面 で対応するマスは上の段で 8 が表記されている (0, 1)、3 番の局面 で対応するマスは (1, 0) となります。
× の手番の 1 番の局面 では次に 〇 が (1, 2) に着手すると 〇 が勝利するので 最善手は (1, 2) となります。従って、2 番と 3 番 の局面の 最善手 は対応する (0, 1) と (1, 0) になります。
先程示したように 現状の ai_abs_dls では、置換表に 同一局面に対する最善手 として 同じ合法手を代入 しているので 1 ~ 8 番の同一局面 に対する最善手としてすべて 同じ合法手が登録 されてしまいます。そのことを実際に確認してみることにします。
下記は前回の記事の最後で ゲーム開始時の局面 に対して深さの上限を 9 とした深さ制限探索で ai_abs_dls が評価値を計算した際の 置換表を tt に代入 するプログラムです。
from ai import ai_abs_dls, ai14s
from marubatsu import Marubatsu
mb = Marubatsu()
eval_params = {"minimax": True}
result = ai_abs_dls(mb, maxdepth=9, eval_func=ai14s, eval_params=eval_params,
use_tt=True, analyze=True)
tt = result["tt"]
下記は、この 置換表に登録された 先程の 1 ~ 3 番の局面の最善手を表示 するプログラムです。最善手 は置換表に登録された tuple の 2 番の要素に代入 されているのでそれを表示しています。実行結果から 1 ~ 3 番のすべての局面 に対して 同一の最善手が記録 されていることが確認できます。また、そのせいで 3 番の局面の最善手 として すでに着手が行われている (1, 2) が記録されていることも確認できます。これが 前回の記事の最後で置換表から PV2 を計算した際に、既に 着手済みのマスに着手を行う という バグが発生した原因 です。
mb = Marubatsu()
mb.move(1, 1)
mb.move(0, 0)
mb.move(1, 0)
print(mb)
print(tt[mb.board_to_str()][2])
mb = Marubatsu()
mb.move(1, 1)
mb.move(2, 0)
mb.move(2, 1)
print(mb)
print(tt[mb.board_to_str()][2])
mb = Marubatsu()
mb.move(1, 1)
mb.move(2, 2)
mb.move(1, 2)
print(mb)
print(tt[mb.board_to_str()][2])
実行結果
Turn x
xO.
.o.
...
(1, 2)
Turn x
..x
.oO
...
(1, 2)
Turn x
...
.o.
.Ox
(1, 2)
バグの修正
このバグを修正する方法の一つは、同一局面を計算する calc_same_boardtexts が 指定した合法手に対応する合法手を計算する ようにするというものです。
具体的には 合法手を代入 する move という仮引数 を追加し、返り値 として計算したそれぞれの同一局面に対して (同一局面, move の同一局面に対応する合法手) という tuple を要素とする set3 を返す ように修正します。
ただし、このような 返り値が変わるような修正 を行うとこれまでに calc_same_boardtexts を利用するプログラムに対する 互換性の問題が発生する ので、仮引数 move を デフォルト値を None とする デフォルト引数 とし、None が代入 されている場合は これまでと同じ返り値を返す ことします。
同一局面に対応する合法手の計算方法
次に、同一局面に対応する合法手 を 計算する方法 について考える必要があります。どのような計算を行えば良いかについて少し考えてみて下さい。
下記は 以前の記事で説明した、2 ~ 8 番の同一局面の (x, y) のマスと 1 番の局面のマスの座標 の 対応表 です。例えば 2 番の (x, y) のマスは、1 番の (y, 2 - x) のマスが対応します。
| 同一局面 | (x, y) に対応する元の局面の座標 |
|---|---|
| 2 | (y, 2 - x) |
| 3 | (2 - x, 2 - y) |
| 4 | (2 - y, x) |
| 5 | (2 - x, y) |
| 6 | (x, 2 - y) |
| 7 | (2 - y, 2 - x) |
| 8 | (y, x) |
この表の座標は、下図の 上の段の数字から求めた ものです。具体的には、n 番の局面の (x, y) のマスに 対応する 1 番の局面の座標 を (x, y) から計算する式を考えて求めました。

今回の calc_sameboradtexts の修正で計算する必要があるのは、その逆 の 1 番の局面の (x, y) のマスに 対応する n 番の局面のマスの座標 の計算ですが、その式は上記の表から求めることはできません。そのような式は上図の上段の数字から改めて考えて求めることもできますが、それぞれの計算で行う処理 を 下記の表のようにまとめる ことでその 式を簡単に求める ことができます。
| 同一局面 | 同一局面の座標に対応する 1 番の局面の座標の計算 |
1 番の局面の座標に対応する 同一局面の座標の計算 |
|---|---|---|
| 2 | 反時計回りに 90 度回転 | 時計回りに 90 度回転 |
| 3 | 反時計回りに 180 度回転 | 時計回りに 180 度回転 |
| 4 | 反時計回りに 270 度回転 | 時計回りに 270 度回転 |
| 5 | 左右に反転 | 左右に反転 |
| 6 | 上下に反転 | 上下に反転 |
| 7 | 左下斜めを軸に反転 | 左下斜めを軸に反転 |
| 8 | 右下斜めを軸に反転 | 右下斜めを軸に反転 |
反時計周りと時計回りに 180 度回転 は 同じ操作 なので、上記の表から 2 番と 4 番以外 の 太字の処理 は 同じ処理を行う ことがわかります。また、「反時計回りに 90 度 回転と 時計回りに 270 度 回転」と「反時計回りに 270 度 回転と 時計回りに 90 度 回転」は 同じ処理 です。そのことから、calc_sameboardtexts を下記のプログラムのように修正します。
-
1 行目:デフォルト値を
Noneとする仮引数moveを追加する -
2 ~ 8 行目:2 ~ 7 番の同一局面を計算するためのデータに、
moveに対応する合法手を計算するためのデータを追加 する。2、4 番以外 の対応する合法手を計算するためのデータは、同一局面を計算するためのデータと同じ なので、* 2 を記述して 同じデータを繰り返す ように修正する。2、4 番 の対応する合法手を計算するためのデータは、4、2 番の同一局面を計算する処理と同じ なので、それらのデータを 2、4 番のデータに追加した -
9 ~ 12 行目:
boardtextsに 1 番の局面に対応するデータを記録する際に、moveがNoneの場合はこれまでと同じ処理を行うようし、そうでない場合は(局面を表す文字列、move)という tuple を要素とする set を代入するように修正する -
13 行目:2 ~ 8 番の同一局面に対する繰り返し処理を行う際に、先程
data追加したデータを変数に代入するように修正する -
18 ~ 23 行目:
boardtextsに 2 ~ 7 番の局面に対応するデータを記録する。moveがNoneの場合はこれまでと同様の処理を行うようし、そうでない場合は先ほどdataに追加したデータを使ってmoveに対応する同一局面の座標を計算し、(局面を表す文字列、move に対応する合法手)という tuple を要素とする set を代入するように修正する
1 def calc_same_boardtexts(mb, move=None):
2 data = [ [ 0, 0, 1, 1, -1, 0, 1, 0, -1, 0, 1, 0],
3 [ 1, -1, 0, 1, 0, -1] * 2,
4 [ 1, 0, -1, 0, 1, 0, 0, 0, 1, 1, -1, 0],
5 [ 1, -1, 0, 0, 0, 1] * 2,
6 [ 0, 1, 0, 1, 0, -1] * 2,
7 [ 1, 0, -1, 1, -1, 0] * 2,
8 [ 0, 0, 1, 0, 1, 0] * 2, ]
9 if move is None:
10 boardtexts = set([mb.board_to_str()])
11 else:
12 boardtexts = set([(mb.board_to_str(), move)])
13 for xa, xb, xc, ya, yb, yc, xa2, xb2, xc2, ya2, yb2, yc2 in data:
14 txt = ""
15 for x in range(mb.BOARD_SIZE):
16 for y in range(mb.BOARD_SIZE):
17 txt += mb.board[xa * 2 + xb * x + xc * y][ya * 2 + yb * x + yc * y]
18 if move is None:
19 boardtexts.add(txt)
20 else:
21 x, y = move
22 x, y = xa2 * 2 + xb2 * x + xc2 * y, ya2 * 2 + yb2 * x + yc2 * y
23 boardtexts.add((txt, (x, y)))
24 return boardtexts
行番号のないプログラム
def calc_same_boardtexts(mb, move=None):
data = [ [ 0, 0, 1, 1, -1, 0, 1, 0, -1, 0, 1, 0],
[ 1, -1, 0, 1, 0, -1] * 2,
[ 1, 0, -1, 0, 1, 0, 0, 0, 1, 1, -1, 0],
[ 1, -1, 0, 0, 0, 1] * 2,
[ 0, 1, 0, 1, 0, -1] * 2,
[ 1, 0, -1, 1, -1, 0] * 2,
[ 0, 0, 1, 0, 1, 0] * 2, ]
if move is None:
boardtexts = set([mb.board_to_str()])
else:
boardtexts = set([(mb.board_to_str(), move)])
for xa, xb, xc, ya, yb, yc, xa2, xb2, xc2, ya2, yb2, yc2 in data:
txt = ""
for x in range(mb.BOARD_SIZE):
for y in range(mb.BOARD_SIZE):
txt += mb.board[xa * 2 + xb * x + xc * y][ya * 2 + yb * x + yc * y]
if move is None:
boardtexts.add(txt)
else:
x, y = move
x, y = xa2 * 2 + xb2 * x + xc2 * y, ya2 * 2 + yb2 * x + yc2 * y
boardtexts.add((txt, (x, y)))
return boardtexts
修正箇所
-def calc_same_boardtexts(mb):
+def calc_same_boardtexts(mb, move=None):
- data = [ [ 0, 0, 1, 1, -1, 0],
- [ 1, -1, 0, 1, 0, -1],
- [ 1, 0, -1, 0, 1, 0],
- [ 1, -1, 0, 0, 0, 1],
- [ 0, 1, 0, 1, 0, -1],
- [ 1, 0, -1, 1, -1, 0],
- [ 0, 0, 1, 0, 1, 0], ]
+ data = [ [ 0, 0, 1, 1, -1, 0, 1, 0, -1, 0, 1, 0],
+ [ 1, -1, 0, 1, 0, -1] * 2,
+ [ 1, 0, -1, 0, 1, 0, 0, 0, 1, 1, -1, 0],
+ [ 1, -1, 0, 0, 0, 1] * 2,
+ [ 0, 1, 0, 1, 0, -1] * 2,
+ [ 1, 0, -1, 1, -1, 0] * 2,
+ [ 0, 0, 1, 0, 1, 0] * 2, ]
- boardtexts = set([mb.board_to_str()])
+ if move is None:
+ boardtexts = set([mb.board_to_str()])
+ else:
+ boardtexts = set([(mb.board_to_str(), move)])
- for xa, xb, xc, ya, yb, yc in data:
+ for xa, xb, xc, ya, yb, yc, xa2, xb2, xc2, ya2, yb2, yc2 in data:
txt = ""
for x in range(mb.BOARD_SIZE):
for y in range(mb.BOARD_SIZE):
txt += mb.board[xa * 2 + xb * x + xc * y][ya * 2 + yb * x + yc * y]
- boardtexts.add(txt)
+ if move is None:
+ boardtexts.add(txt)
+ else:
+ x, y = move
+ x, y = xa2 * 2 + xb2 * x + xc2 * y, ya2 * 2 + yb2 * x + yc2 * y
+ boardtexts.add((txt, (x, y)))
return boardtexts
上記の修正後に下記のプログラムで先程の 1 番の局面 に対する 同一局面 と、(1, 2) に対応する座標 を計算して表示すると、実行結果のように 対応する座標 として 異なる座標が計算される ことが確認できます。
mb = Marubatsu()
mb.move(1, 1)
mb.move(0, 0)
mb.move(1, 0)
boardtexts = calc_same_boardtexts(mb, (1, 2))
for boardtext, move in boardtexts:
print(boardtext, move)
実行結果
....o..ox (0, 1)
....o.xo. (0, 1)
...oo.x.. (1, 2)
....oo..x (1, 0)
xo..o.... (2, 1)
..x.oo... (1, 0)
.ox.o.... (2, 1)
x..oo.... (1, 2)
ai_abs_dls の修正
次に、ai_abs_dls を下記のように calc_same_boardtexts に関する処理を修正 します。
-
7 行目:先程修正した
calc_same_boardtextを利用する ために、calc_same_boardtextsをインポートする処理をコメント にする。なお、この処理は util.py のcalc_same_boardtextsを今回の記事の内容で 修正した後は再び必要になる ので、今回の記事の ai_new.py や 次回以降の ai.py では再び コメントを外す ことにする -
10 行目:
calc_same_boardtextの実引数に最善手を表すbestmoveを記述する -
18、19 行目:
boardtxtlistから同一局面に対応する最善手を取り出してmoveに代入するようにし、それを置換表に登録するように修正する
1 from ai import ai_by_mmscore, dprint
2 from copy import deepcopy
3
4 @ai_by_mmscore
5 def ai_abs_dls(mb, debug=False, timelimit_pc=None, maxdepth=1, eval_func=None,
6 eval_params={}, use_tt=False, tt=None):
元と同じなので省略
7 # from util import calc_same_boardtexts
8
9 if use_tt:
10 boardtxtlist = calc_same_boardtexts(mborig, bestmove)
11 if score <= alphaorig:
12 upper_bound = score
13 elif score < betaorig:
14 lower_bound = score
15 upper_bound = score
16 else:
17 lower_bound = score
18 for boardtxt, move in boardtxtlist:
19 tt[boardtxt] = (lower_bound, upper_bound, move)
20 return score
元と同じなので省略
行番号のないプログラム
from ai import ai_by_mmscore, dprint
from copy import deepcopy
@ai_by_mmscore
def ai_abs_dls(mb, debug=False, timelimit_pc=None, maxdepth=1, eval_func=None,
eval_params={}, use_tt=False, tt=None):
count = 0
def ab_search(mborig, depth, tt, alpha=float("-inf"), beta=float("inf")):
nonlocal count
if timelimit_pc is not None and perf_counter() >= timelimit_pc:
raise RuntimeError("time out")
count += 1
if mborig.status != Marubatsu.PLAYING or depth == maxdepth:
return eval_func(mborig, calc_score=True, **eval_params)
if use_tt:
boardtxt = mborig.board_to_str()
if boardtxt in tt:
lower_bound, upper_bound, _ = tt[boardtxt]
if lower_bound == upper_bound:
return lower_bound
elif upper_bound <= alpha:
return upper_bound
elif beta <= lower_bound:
return lower_bound
else:
alpha = max(alpha, lower_bound)
beta = min(beta, upper_bound)
else:
lower_bound = min_score
upper_bound = max_score
alphaorig = alpha
betaorig = beta
legal_moves = mborig.calc_legal_moves()
if mborig.turn == Marubatsu.CIRCLE:
score = float("-inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
abscore = ab_search(mb, depth + 1, tt, alpha, beta)
if abscore > score:
bestmove = (x, y)
score = max(score, abscore)
if score >= beta:
break
alpha = max(alpha, score)
else:
score = float("inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
abscore = ab_search(mb, depth + 1, tt, alpha, beta)
if abscore < score:
bestmove = (x, y)
score = min(score, abscore)
if score <= alpha:
break
beta = min(beta, score)
# from util import calc_same_boardtexts
if use_tt:
boardtxtlist = calc_same_boardtexts(mborig, bestmove)
if score <= alphaorig:
upper_bound = score
elif score < betaorig:
lower_bound = score
upper_bound = score
else:
lower_bound = score
for boardtxt, move in boardtxtlist:
tt[boardtxt] = (lower_bound, upper_bound, move)
return score
min_score = float("-inf")
max_score = float("inf")
if tt is None:
tt = {}
score = ab_search(mb, depth=0, tt=tt, alpha=min_score, beta=max_score)
dprint(debug, "count =", count)
return score, count
修正箇所
from ai import ai_by_mmscore, dprint
from copy import deepcopy
@ai_by_mmscore
def ai_abs_dls(mb, debug=False, timelimit_pc=None, maxdepth=1, eval_func=None,
eval_params={}, use_tt=False, tt=None):
元と同じなので省略
- from util import calc_same_boardtexts
+# from util import calc_same_boardtexts
if use_tt:
- boardtxtlist = calc_same_boardtexts(mborig)
+ boardtxtlist = calc_same_boardtexts(mborig, bestmove)
if score <= alphaorig:
upper_bound = score
elif score < betaorig:
lower_bound = score
upper_bound = score
else:
lower_bound = score
- for boardtxt in boardtxtlist:
+ for boardtxt, move in boardtxtlist:
- tt[boardtxt] = (lower_bound, upper_bound)
+ tt[boardtxt] = (lower_bound, upper_bound, move)
return score
元と同じなので省略
上記の修正後に、下記のプログラムで 前回の記事 と同じ方法で PV を計算 すると、実行結果のように 引き分け になり、最後の行で PV が正しく計算される ことが確認できます。
2025/08/07 修正:最後の if 文の elif を else に修正しました。
mb = Marubatsu()
eval_params = {"minimax": True}
result = ai_abs_dls(mb, maxdepth=9, eval_func=ai14s, eval_params=eval_params,
use_tt=True, analyze=True)
tt = result["tt"]
bestmove = result["bestmove"]
PV = []
while mb.status == Marubatsu.PLAYING:
PV.append(bestmove)
print(bestmove)
x, y = bestmove
if mb.board[x][y] != Marubatsu.EMPTY:
print("そのマスには着手済みです")
break
mb.move(x, y)
print(mb)
boardtxt = mb.board_to_str()
if boardtxt in tt:
_, _, bestmove = tt[boardtxt]
else:
break
print(PV)
実行結果(最初の着手はランダムなので下記と実行結果が異なる場合があります)
(1, 2)
Turn x
...
...
.O.
(2, 2)
Turn o
...
...
.oX
(2, 1)
Turn x
...
..O
.ox
(1, 1)
Turn o
...
.Xo
.ox
(0, 0)
Turn x
O..
.xo
.ox
(0, 2)
Turn o
o..
.xo
Xox
(2, 0)
Turn x
o.O
.xo
xox
(1, 0)
Turn o
oXo
.xo
xox
(0, 1)
winner draw
oxo
Oxo
xox
[(1, 2), (2, 2), (2, 1), (1, 1), (0, 0), (0, 2), (2, 0), (1, 0), (0, 1)]
move ordering を行う αβ 法の反復深化の実装と検証
置換表に最善手が正しく記録されるようになったので、前回の記事で説明した下記の 反復深化を利用した move ordering を実装 することにします。
- 深さ制限探索を行う際に 置換表を利用 する
- 深さの上限を $\boldsymbol{d}$ とする深さ制限探索を行う際に、深さの上限を $\boldsymbol{d - 1}$ とした深さ制限探索の 置換表を元に move ordering を行う
そのためには、置換表に記録された最善手を利用した move ordering を行う ように ai_abs_dls を修正す る必要があります。どのように修正すればよいかについて少し考えてみて下さい。
置換表を利用した move ordering の実装
置換表に記録された最善手を利用した move ordering を行うためには、その 置換表を代入する仮引数を ai_abs_dls に追加 する必要があります。そこで、move ordering を行うための置換表を代入する tt_for_mo という仮引数を追加 することにします。また、この仮引数は None をデフォルト値 とするデフォルト引数とし、None が代入 されている場合は move ordering を行わない ことにします。
下記は、そのように ai_abs_dls を修正したプログラムです。
-
3 行目:デフォルト値を
Noneとする仮引数tt_for_moを追加する -
9 ~ 15 行目:
tt_for_moがNoneでない場合の move ordering の処理を行う -
10、11 行目:12 行目で必要となる
boardtxtは 6、7 行目でuse_ttがTrueの場合しか計算されていないので、use_ttがFalseの場合に計算するようにした。なお、boardtxtを常に計算するように修正するという方法も考えられるが、use_tt=False、tt_for_mo=Falseの場合は無駄な処理が行われることになるので採用を見送った -
12 ~ 15 行目:move ordering を行うための置換表に現在の局面のデータが登録されている場合に、最善手を先頭に移動するという move ordering の処理を行う。置換表に登録されている下界と上界の情報は move ordering には必要がないので
_という変数に代入した。14、15 行目の処理について忘れた方は 以前の記事 を復習すること
1 @ai_by_mmscore
2 def ai_abs_dls(mb, debug=False, timelimit_pc=None, maxdepth=1, eval_func=None,
3 eval_params={}, use_tt=False, tt=None, tt_for_mo=None):
4 count = 0
5 def ab_search(mborig, depth, tt, alpha=float("-inf"), beta=float("inf")):
元と同じなので省略
6 if use_tt:
7 boardtxt = mborig.board_to_str()
元と同じなので省略
8 legal_moves = mborig.calc_legal_moves()
9 if tt_for_mo is not None:
10 if not use_tt:
11 boardtxt = mborig.board_to_str()
12 if boardtxt in tt_for_mo:
13 _, _, bestmove = tt_for_mo[boardtxt]
14 index = legal_moves.index(bestmove)
15 legal_moves[0], legal_moves[index] = legal_moves[index], legal_moves[0]
16 if mborig.turn == Marubatsu.CIRCLE:
元と同じなので省略
行番号のないプログラム
@ai_by_mmscore
def ai_abs_dls(mb, debug=False, timelimit_pc=None, maxdepth=1, eval_func=None,
eval_params={}, use_tt=False, tt=None, tt_for_mo=None):
count = 0
def ab_search(mborig, depth, tt, alpha=float("-inf"), beta=float("inf")):
nonlocal count
if timelimit_pc is not None and perf_counter() >= timelimit_pc:
raise RuntimeError("time out")
count += 1
if mborig.status != Marubatsu.PLAYING or depth == maxdepth:
return eval_func(mborig, calc_score=True, **eval_params)
if use_tt:
boardtxt = mborig.board_to_str()
if boardtxt in tt:
lower_bound, upper_bound, _ = tt[boardtxt]
if lower_bound == upper_bound:
return lower_bound
elif upper_bound <= alpha:
return upper_bound
elif beta <= lower_bound:
return lower_bound
else:
alpha = max(alpha, lower_bound)
beta = min(beta, upper_bound)
else:
lower_bound = min_score
upper_bound = max_score
alphaorig = alpha
betaorig = beta
legal_moves = mborig.calc_legal_moves()
if tt_for_mo is not None:
if not use_tt:
boardtxt = mborig.board_to_str()
if boardtxt in tt_for_mo:
_, _, bestmove = tt_for_mo[boardtxt]
index = legal_moves.index(bestmove)
legal_moves[0], legal_moves[index] = legal_moves[index], legal_moves[0]
if mborig.turn == Marubatsu.CIRCLE:
score = float("-inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
abscore = ab_search(mb, depth + 1, tt, alpha, beta)
if abscore > score:
bestmove = (x, y)
score = max(score, abscore)
if score >= beta:
break
alpha = max(alpha, score)
else:
score = float("inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
abscore = ab_search(mb, depth + 1, tt, alpha, beta)
if abscore < score:
bestmove = (x, y)
score = min(score, abscore)
if score <= alpha:
break
beta = min(beta, score)
# from util import calc_same_boardtexts
if use_tt:
boardtxtlist = calc_same_boardtexts(mborig, bestmove)
if score <= alphaorig:
upper_bound = score
elif score < betaorig:
lower_bound = score
upper_bound = score
else:
lower_bound = score
for boardtxt, move in boardtxtlist:
tt[boardtxt] = (lower_bound, upper_bound, move)
return score
min_score = float("-inf")
max_score = float("inf")
if tt is None:
tt = {}
score = ab_search(mb, depth=0, tt=tt, alpha=min_score, beta=max_score)
dprint(debug, "count =", count)
return score, count
修正箇所
@ai_by_mmscore
def ai_abs_dls(mb, debug=False, timelimit_pc=None, maxdepth=1, eval_func=None,
- eval_params={}, use_tt=False, tt=None):
+ eval_params={}, use_tt=False, tt=None, tt_for_mo=None):
count = 0
def ab_search(mborig, depth, tt, alpha=float("-inf"), beta=float("inf")):
元と同じなので省略
if use_tt:
boardtxt = mborig.board_to_str()
元と同じなので省略
legal_moves = mborig.calc_legal_moves()
+ if tt_for_mo is not None:
+ if not use_tt:
+ boardtxt = mborig.board_to_str()
+ if boardtxt in tt_for_mo:
+ _, _, bestmove = tt_for_mo[boardtxt]
+ index = legal_moves.index(bestmove)
+ legal_moves[0], legal_moves[index] = legal_moves[index], legal_moves[0
if mborig.turn == Marubatsu.CIRCLE:
元と同じなので省略
上記の修正後に move ordering を 行う場合と行わない場合の処理を比較 することにします。下記はゲーム開始時の局面に対する深さの上限を 9 とした深さ制限探索で move ordering を行わない 場合の 処理時間、計算したノードの数、計算された評価値、最善手の一覧 を表示するプログラムです。
mb = Marubatsu()
result = ai_abs_dls(mb, maxdepth=9, eval_func=ai14s, eval_params=eval_params,
use_tt=True, analyze=True)
print(result["time"], result["count"], result["score"], result["candidate"])
実行結果
0.09531459957361221 1175 0.0 [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
下記は 上記で計算した置換表を利用した move ordering を行う 場合のプログラムです。同じ局面に対して同じ深さの上限 で探索を行うので、置換表に記録された最善手を着手した子ノードを先頭に移動することで 100 % 正しい move ordering が行われます。その結果、処理時間と計算したノードの数は約半分になる ことが確認できました。また、計算した評価値と最善手の一覧が同じ であることも確認できます。
result = ai_abs_dls(mb, maxdepth=9, eval_func=ai14s, eval_params=eval_params,
use_tt=True, analyze=True, tt_for_mo=result["tt"])
print(result["time"], result["count"], result["score"], result["candidate"])
実行結果
0.05051949992775917 538 0.0 [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
ai_ab_iddfs の修正
次に、move ordering を行う αβ 法の反復深化を実装 することにします。具体的には、以前の記事 で実装した αβ法 の反復深化の処理を行う ai_ab_iddfs に move ordering を行うか どうかを表す moveordering という仮引数を追加 することにします。また、moveordering に関しては下記のような処理を行うことにします。
-
αβ 法の反復深化 では move ordering をしたほうが効率が良い ので、デフォルト値を
Trueとしたデフォルト引数とする -
反復深化を利用した move ordering では 置換表の利用と置換表の共有が必須 であるので、
moveorderingがTrueの場合はuse_tt=True、share_tt=Trueとする
また、上記以外に下記の修正を行いました。
-
置換表の利用 と 置換表の共有 は 行ったほうが効率が良い ので
use_ttとshare_ttの デフォルト値をTrueに修正 した - これまでは
ai_ab_iddfsの返り値 は仮引数analyzeの値に関わらず 常に最善手のみを返していた が、analyze=Trueの場合 はそれぞれの 深さ上限探索で計算された返り値を要素とする list を返す ように修正することで、反復深化の 処理を分析できる ようにした -
前回の記事で
@ai_by_mmscoreでデコレートした関数を呼び指す際の実引数にanalyze=Trueを記述 した場合の 返り値に計算したノードの数が記録される ようになったので、それらをdebug=Trueを実引数に記述して呼び出した際に 表示する ようにした
下記はそのように ai_ab_iddfs を修正したプログラムです。
-
4 行目:
use_ttとshare_ttのデフォルト値をTrueに修正し、デフォルト値をTrueとした仮引数moveorderingを追加する -
7 ~ 10 行目:
moverorderingがTrueの場合はuse_ttとshare_ttをTrueとし、move ordering のための置換表を空の dict で初期化する -
11、12 行目:
moverorderingがFalseの場合は move ordering のための置換表を None で初期化する - 13 行目:これまでは最善手を表す変数を合法手の一覧からランダムに選択した値で初期化していたが、よく考えるとこの値は深さの上限を 1 とした深さ制限探索の結果ですぐに上書きされるためまず使われないので、最初の合法手で初期化するように修正した
- 14 行目:計算したノードの数の合計を記録する変数を 0 で初期化する
- 15 行目:深さ制限探索の結果の一覧を記録する変数を空の list で初期化する
-
21 行目:
analyze=Trueの場合と move ordering を行う場合はai_abs_dlsのキーワード引数にanalyze=Trueを記述する必要があるのでanalyze=analyze or moveorderingのように修正した。また、キーワード引数tt_for_mo=tt_for_moを追加した -
25、26 行目:move ordering を行う場合は次の深さ制限探索の move ordering を行う際に利用する置換表を表す
tt_for_moに今回の深さ制限探索で計算した置換表を代入する - 27 行目:この後のデバッグ表示で表示する、ここまでの処理時間を計算する
- 28 行目:深さ制限探索の結果の一覧を記録する list の要素に先程計算した深さ制限探索の結果を追加する
-
29 ~ 35 行目:
ai_abs_dlsのキーワード引数にanalyze=Trueを記述して呼び出した際のデバッグ表示に下記の内容を表示するように改良した- 「直前の深さ上限探索の処理時間」/「ここまでの処理時間」を表示する
- 「直前の深さ上限探索で計算したノードの数」/「ここまでで計算したノードの数の合計」を表示する
なお、最善手はresult["bestmove"]記録されるようになったので、28 行目の処理はそれを代入するように修正した
-
40 ~ 43 行目:
analyze=Trueの場合は深さ制限探索の結果の一覧を表すデータを、そうでない場合は最善手を返すように修正した
1 from time import perf_counter
2
3 def ai_ab_iddfs(mb, debug=False, timelimit=10, eval_func=None, eval_params={},
4 use_tt=True, share_tt=True, analyze=False, moveordering=True):
5 starttime = perf_counter()
6 timelimit_pc = starttime + timelimit
7 if moveordering:
8 use_tt = True
9 share_tt = True
10 tt_for_mo = {}
11 else:
12 tt_for_mo = None
13 bestmove = mb.calc_legal_moves()[0]
14 totalcount = 0
15 resultlist = []
16 for maxdepth in range(9 - mb.move_count):
17 try:
18 result = ai_abs_dls(mb, maxdepth=maxdepth, timelimit_pc=timelimit_pc,
19 eval_func=eval_func, eval_params=eval_params,
20 use_tt=use_tt, share_tt=share_tt,
21 analyze=analyze or moveordering, tt_for_mo=tt_for_mo)
22 except RuntimeError:
23 dprint(debug, "time out")
24 break
25 if moveordering:
26 tt_for_mo = result["tt"]
27 totaltime = perf_counter() - starttime
28 resultlist.append(result)
29 if analyze or moveordering:
30 candidate = result["candidate"]
31 bestmove = result["bestmove"]
32 count = result["count"]
33 time = result["time"]
34 totalcount += count
35 dprint(debug, f"maxdepth: {maxdepth}, time: {time:6.2f}/{totaltime:6.2f} ms, count {count:5}/{totalcount:5}, bestmove: {bestmove}, candidate: {candidate}")
36 else:
37 bestmove = result
38 dprint(debug, f"maxdepth: {maxdepth}, time: {totaltime:6.2f} ms, bestmove: {bestmove}")
39 dprint(debug, f"totaltime: {perf_counter() - starttime: 6.2f} ms")
40 if analyze:
41 return resultlist
42 else:
43 return bestmove
行番号のないプログラム
from time import perf_counter
def ai_ab_iddfs(mb, debug=False, timelimit=10, eval_func=None, eval_params={},
use_tt=True, share_tt=True, analyze=False, moveordering=True):
starttime = perf_counter()
timelimit_pc = starttime + timelimit
if moveordering:
use_tt = True
share_tt = True
tt_for_mo = {}
else:
tt_for_mo = None
bestmove = mb.calc_legal_moves()[0]
totalcount = 0
resultlist = []
for maxdepth in range(9 - mb.move_count):
try:
result = ai_abs_dls(mb, maxdepth=maxdepth, timelimit_pc=timelimit_pc,
eval_func=eval_func, eval_params=eval_params,
use_tt=use_tt, share_tt=share_tt,
analyze=analyze or moveordering, tt_for_mo=tt_for_mo)
except RuntimeError:
dprint(debug, "time out")
break
if moveordering:
tt_for_mo = result["tt"]
totaltime = perf_counter() - starttime
resultlist.append(result)
if analyze or moveordering:
candidate = result["candidate"]
bestmove = result["bestmove"]
count = result["count"]
time = result["time"]
totalcount += count
dprint(debug, f"maxdepth: {maxdepth}, time: {time:6.2f}/{totaltime:6.2f} ms, count {count:5}/{totalcount:5}, bestmove: {bestmove}, candidate: {candidate}")
else:
bestmove = result
dprint(debug, f"maxdepth: {maxdepth}, time: {totaltime:6.2f} ms, bestmove: {bestmove}")
dprint(debug, f"totaltime: {perf_counter() - starttime: 6.2f} ms")
if analyze:
return resultlist
else:
return bestmove
修正箇所
from time import perf_counter
def ai_ab_iddfs(mb, debug=False, timelimit=10, eval_func=None, eval_params={},
- use_tt=False, share_tt=False, analyze=False):
+ use_tt=True, share_tt=True, analyze=False, moveordering=True):
starttime = perf_counter()
timelimit_pc = starttime + timelimit
+ if moveordering:
+ use_tt = True
+ share_tt = True
+ tt_for_mo = {}
+ else:
+ tt_for_mo = None
- bestmove = choice(mb.calc_legal_moves())
+ bestmove = mb.calc_legal_moves()[0]
+ totalcount = 0
+ resultlist = []
for maxdepth in range(9 - mb.move_count):
try:
result = ai_abs_dls(mb, maxdepth=maxdepth, timelimit_pc=timelimit_pc,
eval_func=eval_func, eval_params=eval_params,
use_tt=use_tt, share_tt=share_tt,
- analyze=analyze)
+ analyze=analyze or moveordering, tt_for_mo=tt_for_mo)
except RuntimeError:
dprint(debug, "time out")
break
+ if moveordering:
+ tt_for_mo = result["tt"]
+ totaltime = perf_counter() - starttime
+ resultlist.append(result)
- if analyze:
+ if analyze or moveordering:
candidate = result["candidate"]
- bestmove = choice(candidate)
+ bestmove = result["bestmove"]
+ count = result["count"]
+ time = result["time"]
+ totalcount += count
- dprint(debug, f"maxdepth: {maxdepth}, time: {perf_counter() - starttime:6.2f} ms, bestmove: {bestmove}, candidate: {candidate}")
+ dprint(debug, f"maxdepth: {maxdepth}, time: {time:6.2f}/{totaltime:6.2f} ms, count {count:5}/{totalcount:5}, bestmove: {bestmove}, candidate: {candidate}")
else:
bestmove = result
dprint(debug, f"maxdepth: {maxdepth}, time: {totaltime:6.2f} ms, bestmove: {bestmove}")
dprint(debug, f"totaltime: {perf_counter() - starttime: 6.2f} ms")
- return bestmove
+ if analyze:
+ return resultlist
+ else:
+ return bestmove
上記の修正後に下記のプログラムでゲーム開始時の局面に対して analyze=False、moveordering=False を記述して ai_ab_iddfs を呼び出すと、修正前と同様 に 深さの上限ごとの処理時間と最善手が表示 され、返り値として最善手のみ が返されます。
print(ai_ab_iddfs(mb, timelimit=10, debug=True, eval_func=ai14s,
eval_params=eval_params, analyze=False, moveordering=False))
実行結果
maxdepth: 0, time: 0.00 ms, bestmove: (1, 1)
maxdepth: 1, time: 0.00 ms, bestmove: (1, 1)
maxdepth: 2, time: 0.01 ms, bestmove: (1, 1)
maxdepth: 3, time: 0.04 ms, bestmove: (1, 1)
maxdepth: 4, time: 0.10 ms, bestmove: (1, 1)
maxdepth: 5, time: 0.21 ms, bestmove: (1, 1)
maxdepth: 6, time: 0.27 ms, bestmove: (1, 1)
maxdepth: 7, time: 0.34 ms, bestmove: (1, 2)
maxdepth: 8, time: 0.42 ms, bestmove: (0, 0)
totaltime: 0.42 ms
(0, 0)
次に、下記のプログラムでゲーム開始時の局面に対して analyze=True、moveordering=False を記述して ai_ab_iddfs を呼び出すと、実行結果のように 深さの上限ごと の「処理時間/処理時間の合計」、「計算されたノードの数/計算されたノードの数の合計」が表示されるようになったことが確認できます。また、 返り値として深さの上限ごとの結果を表す list が返されることが確認できます。
resultlist = ai_ab_iddfs(mb, timelimit=10, debug=True, eval_func=ai14s,
eval_params=eval_params, analyze=True, moveordering=False)
print(resultlist)
実行結果
maxdepth: 0, time: 0.00/ 0.00 ms, count 9/ 9, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 1, time: 0.01/ 0.01 ms, count 33/ 42, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 2, time: 0.01/ 0.02 ms, count 81/ 123, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 3, time: 0.03/ 0.04 ms, count 206/ 329, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 4, time: 0.03/ 0.07 ms, count 431/ 760, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 5, time: 0.06/ 0.13 ms, count 927/ 1687, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 6, time: 0.17/ 0.30 ms, count 1121/ 2808, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 7, time: 0.10/ 0.39 ms, count 1161/ 3969, bestmove: (1, 2), candidate: [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth: 8, time: 0.07/ 0.46 ms, count 1175/ 5144, bestmove: (2, 0), candidate: [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
totaltime: 0.46 ms
[{'candidate': [(1, 1)], 'score_by_move': {(0, 0): 1.5, (1, 0): 1.0, (2, 0): 1.5, (0, 1): 1.0, (1, 1): 2.0, (2, 1): 1.0, (0, 2): 1.5, (1, 2): 1.0, (2, 2): 1.5}, 'tt': {}, 'time': 0.0022270996123552322, 'bestmove': (1, 1), 'score': 2.0, 'count': 9}, 以下略
次に、下記のプログラムでゲーム開始時の局面に対して analyze=True、moveordering=True を記述して ai_ab_iddfs を呼び出すと、実行結果から move ordering を行わない場合と比べて 処理時間と計算したノードの数が 減っている ことが確認できます。
resultlist_mo = ai_ab_iddfs(mb, timelimit=10, debug=True, eval_func=ai14s,
eval_params=eval_params, analyze=True, moveordering=True)
実行結果
maxdepth: 0, time: 0.00/ 0.00 ms, count 9/ 9, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 1, time: 0.01/ 0.01 ms, count 33/ 42, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 2, time: 0.01/ 0.02 ms, count 66/ 108, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 3, time: 0.03/ 0.05 ms, count 162/ 270, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 4, time: 0.02/ 0.07 ms, count 272/ 542, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 5, time: 0.03/ 0.10 ms, count 446/ 988, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 6, time: 0.04/ 0.14 ms, count 578/ 1566, bestmove: (1, 1), candidate: [(1, 1)]
maxdepth: 7, time: 0.03/ 0.17 ms, count 530/ 2096, bestmove: (1, 2), candidate: [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
maxdepth: 8, time: 0.03/ 0.20 ms, count 533/ 2629, bestmove: (0, 0), candidate: [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
totaltime: 0.20 ms
move ordering を行う αβ 法の反復深化の効率の検証
move ordering を行う αβ 法の反復深化 の 効率の検証 を行うために、ゲーム開始時の局面に対する下記の 3 種類の探索 で 計算されたノードの数を比較 することにします。
- 深さの上限を 1 ~ 9 とした場合の 深さ制限探索
- move ordering を行わない、深さの上限が 1 ~ 9 までの深さ制限探索を行った 反復深化
- move ordering を行う、深さの上限が 1 ~ 9 までの深さ制限探索を行った 反復深化
以前の記事で計算したノードの数と処理時間はほぼ比例することを示したので、今回の記事では計算時間の比較は行いません。興味がある方は比較してみて下さい。
深さの上限を 1 ~ 9 とした場合の 深さ制限探索 は、先程行った move ordering を行わない反復深化 で行った それぞれの深さ制限探索の結果 から確認することができます。
下記は先ほどの結果から それぞれの場合の計算されたノードの数 をまとめた表です。また、反復深化の列 では、深さ制限探索の数で割った比率 を / の右に記しました。なお、先ほどの実行結果で表示される maxdepth の値は、ルートノードの子ノードから数えた深さの上限なので、下記の表の深さの上限は実行結果の maxdepth に 1 を加えたものです。
| 深さの上限 | 深さ制限探索 | 反復深化 mo なし | 反復深化 mo あり |
|---|---|---|---|
| 1 | 9 | 9/1.00 | 9/1.00 |
| 2 | 33 | 43/1.30 | 42/1.27 |
| 3 | 81 | 123/1.52 | 108/1.33 |
| 4 | 206 | 329/1.60 | 267/1.30 |
| 5 | 431 | 760/1.76 | 533/1.24 |
| 6 | 927 | 1687/1.82 | 980/1.06 |
| 7 | 1121 | 2808/2.50 | 1556/1.39 |
| 8 | 1161 | 3969/3.42 | 2080/1.79 |
| 9 | 1175 | 5144/4.38 | 2612/2.22 |
下記は、上記のうちの 計算したノードの数をグラフ化 するプログラムです。
- 3 行目:深さ制限探索で計算されたノードの数を記録する変数を空の list で初期化する
- 4 行目:move ordering を行わない反復深化で計算されたノードの数を数える変数を 0 で初期化する
- 5 行目:move ordering を行わない反復深化で計算されたノードの数を記録する変数を空の list で初期化する
- 6 ~ 10 行目:move ordering を行わない反復深化の計算結果から、それぞれの深さの上限での深さ制限探索と反復深化で計算されたノードの数を記録する
- 12 ~ 17 行目:上記と同様の方法で move ordering を行う反復深化の計算結果から、それぞれの深さの上限での反復深化で計算されたノードの数を記録する
-
19 ~ 25 行目:上記の計算結果をグラフ化する。19 行目の
maxdepthlistは横軸の深さの上限の一覧を表すデータであり、これを用意しないと横軸の数値が 0 ~ 8 となってしまう
1 import matplotlib.pyplot as plt
2
3 countlist = []
4 totalcount = 0
5 totalcountlist = []
6 for result in resultlist:
7 count = result["count"]
8 totalcount += count
9 countlist.append(count)
10 totalcountlist.append(totalcount)
11
12 totalcount_mo = 0
13 totalcountlist_mo = []
14 for result in resultlist_mo:
15 count_mo = result["count"]
16 totalcount_mo += count_mo
17 totalcountlist_mo.append(totalcount_mo)
18
19 maxdepthlist = range(1, 10)
20 plt.plot(maxdepthlist, countlist, label="深さ制限探索")
21 plt.plot(maxdepthlist, totalcountlist, label="反復深化 move ordering なし")
22 plt.plot(maxdepthlist, totalcountlist_mo, label="反復深化 move ordering あり")
23 plt.xlabel("深さの上限")
24 plt.ylabel("計算したノードの数")
25 plt.legend()
行番号のないプログラム
import matplotlib.pyplot as plt
countlist = []
totalcount = 0
totalcountlist = []
for result in resultlist:
count = result["count"]
totalcount += count
countlist.append(count)
totalcountlist.append(totalcount)
totalcount_mo = 0
totalcountlist_mo = []
for result in resultlist_mo:
count_mo = result["count"]
totalcount_mo += count_mo
totalcountlist_mo.append(totalcount_mo)
maxdepthlist = range(1, 10)
plt.plot(maxdepthlist, countlist, label="深さ制限探索")
plt.plot(maxdepthlist, totalcountlist, label="反復深化 move ordering なし")
plt.plot(maxdepthlist, totalcountlist_mo, label="反復深化 move ordering あり")
plt.xlabel("深さの上限")
plt.ylabel("計算したノードの数")
plt.legend()
実行結果
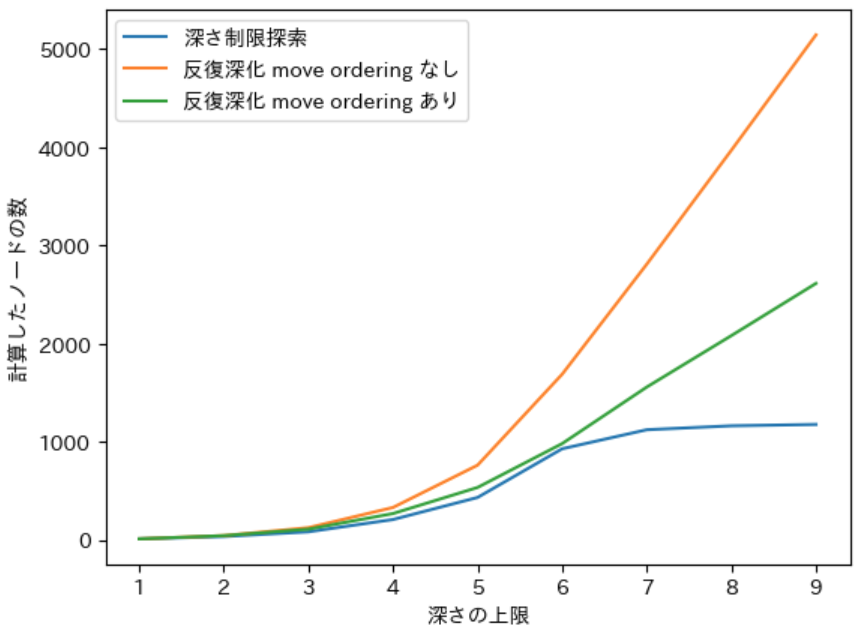
深さの上限が 1 の場合
深さの上限が 1 の場合は、すべての 9 つの子ノードの計算を行う必要がある ため 枝狩りは行われません。従って、すべての場合 で計算されるノードの数は 9 となります。
深さの上限が 2 ~ 6 の場合
先程の表と実行結果のグラフから、〇× ゲームのゲーム開始時の局面に対する探索は、深さの上限が 2 ~ 6 までの場合は下記のような性質を持つことがわかります。
- 深さ制限探索 と、move ordering を行う反復深化 では、計算するノードの数の 比率は 1.06 ~ 1.33 倍 であり、グラフの見た目からも その値は 大きくは変わらない
- 深さ制限探索 と、move ordering を行わない反復深化 では、計算するノードの数の 比率は 1.30 ~ 1.82 倍 であり、グラフの見た目からも 反復深化のほうが 深さの上限が大きくなるにつれて比率が高く なる
このことから、〇× ゲームのゲーム開始時の局面 に対しては move ordering を行う反復深化 は、深さ制限探索 と ほぼ同じ効率 で計算を行うことができることが確認できます。
枝狩り は、max ノードでは β 値以上の評価値が計算された場合に、残りの子ノードの計算を省略 するという処理です。従って、子ノードの数が多い程枝狩りの効率が高くなる ことが期待できます。〇× ゲームの場合は、子ノードの数が最大でも 9 しかありませんが、将棋や囲碁など 子ノードの数がもっと多いゲーム の場合は、反復深化のほうが 深さ制限探索よりも 高い効率で計算を行うことができる場合 もあるようです。
そのことは、下記の Chess Programming Wiki の反復深化の記事内で「It has been noticed, that even if one is about to search to a given depth, that iterative deepening is faster than searching for the given depth immediately. This is due to dynamic move ordering techniques(以下略)(筆者意訳:特定の深さまでの探索を行う場合に、その深さの上限で深さ制限探索を行うよりも、反復深化のほうが速いことが報告されている。その原因は move ordering によるものである)」のように説明されています。
深さの上限が 7 ~ 9 の場合
先程の表とグラフから 深さの上限が 7 ~ 9 の場合は 深さ制限探索 で計算するノードの数は ほとんど増えない のに対して、反復深化 で計算するノードの数は move ordering の有無に関わらず 増えていく ことが確認できます。
深さの上限が 7 ~ 9 の場合に上記のような結果になる理由は、〇× ゲーム が 着手を行うにつれて合法手の数が少なくなる という性質があるからです。先程説明したように、αβ 法では枝狩りは子ノードの数が多い程効率が高くなります。〇× ゲームの深さが 7、8 の局面のノード には 子ノードが最大でも 2、1 しか存在しない ため、〇× ゲームの場合は 深さの上限が 7 以上の深さ制限探索 では、実際に 計算されるノードの数 が 1121、1161、1175 のように ほとんど変わらなくなります。
計算されるノードの数がほぼ同じ であるということは、move ordering を行った場合 に計算されるノードの数も 大きく変わらない ことになります。実際に move ordering を行った場合の反復深化 で、深さの上限が 7 ~ 9 の深さ制限探索で計算されたノードの数は 576、524、532 と ほとんど変わりません。
これが、深さの上限が 7 ~ 9 の場合は、深さ制限探索 で計算されるノードの数が ほとんど変わらない のに対して、反復深化 で計算されるノードの数が 増えていく理由 です。
このような現象は、ゲームの終盤になると合法手が減っていくようなゲーム で発生しますが、そのことは下記のような理由から 大きな問題にはならない のではないかと思います。
- ゲームの 序盤から中盤の局面 では 合法手の数が多い ので、深さの上限をゲーム木の深さと同じくらい大きくしない限りこの ような現象は生じない
- 多くのゲームでは ゲーム木の規模が大きい ため、序盤から中盤の局面 に対して 上記の現象が発生するほどの深さの上限まで 反復深化を行うには 処理時間がかかりすぎる
- ゲームの終盤 になると、その局面をルートノードとする 部分木の規模が小さくなる ため、上記の現象が発生するような場合は 短い時間で処理を行える ようになる
move ordering を行わない場合の反復深化の効率
反復深化で深さの上限が d まで の深さ制限探索を行う際は、深さの上限が 1 ~ d - 1 までの深さ制限探索を行う必要があります。αβ 法に対する反復深化では それまでの計算結果から move ordering を行う ことで、反復深化の効率を高める という工夫を行なうことができますが、そのような 工夫を行なえない場合 でも 反復深化が使われる ことがあります。
その理由は、木構造のデータ に対して深さの上限が d の 深さ上限探索に必要な処理時間 と、深さの上限が d までの 反復深化に必要な処理時間の比率 が、下記のノートのような理由から 一般的に 2 以下になる からです。また、子ノードの数が多いほど比率は 1 に近づきます。従って move ordering などの処理の効率化を行わない反復深化を行っても、一般的にその 処理時間は深さ制限探索と比べて大きくは増えない ことがわかります。
一方、木構造のデータ は 一般的 に 深さが 1 増えるごと にノードの数が 数倍になる という 指数関数的に増えます。従って、深さ制限探索と反復深化で 同じ時間で探索できる深さの上限を比較 すると、その差は一般的には 1 以下 になるため、結果は大きく変わりません。
深さ制限探索と反復深化の処理時間の比率が一般的に 2 以下になり、子ノードの数が多くなると 1 に近づく理由を説明します。
ゲーム木の探索に必要な処理時間は、探索中に計算したノードの数にほぼ比例します。以前の記事 で説明したように、探索するゲーム木のリーフノードの数で処理時間を比較することがあるので、ゲーム木のリーフノードの数で処理時間を比較することにします。また、計算を簡単に行えるようにするために、リーフノード以外のノードの子ノードの数が等しい バランス木で比較を行うことにします。
子ノードの数が $n$ で深さが $d$ のバランス木のリーフノードの数は $n^d$ となります。従って、深さの上限がが $d$ の深さ制限探索の処理時間は $n^d$ に比例すると考えることができます。
反復深化では深さが 1 ~ d までの深さ制限探索を行うので、計算するリーフノードの数の合計は下記の式で表され、処理時間はこの式の値に比例すると考えることができます。
$\sum_{i=0}^{d}n^i = n^0 + n^1 + n^2 + ・・・ n^d$
以前の記事で説明したように、$n ≧ 2$ の場合は下記の式が成り立ちます。
$\sum_{i=0}^{d}n^i < \frac{n}{n-1}n^d$
$\frac{n}{n-1}$ は $n = 2$ の場合に 2 となり、$n$ が大きくなると 1 に近づいていくので、深さ制限探索と反復深化の処理時間の比率は 2 以下になり、子ノードの数が多くなると 1 に近づくことになります。
今回の記事のまとめ
今回の記事では、前回の記事のバグを修正し、反復深化を利用した move ordering を実装 しました。また、反復深化を利用した move ordering と深さ制限探索と効率を比較しました。多くのゲームでは、move ordering を行う反復深化の効率 は 深さ制限探索よりも高くなる ようです。次回の記事では反復深化で良く使われる別の効率の良いアルゴリズムを紹介する予定です。
本記事で入力したプログラム
| リンク | 説明 |
|---|---|
| marubatsu.ipynb | 本記事で入力して実行した JupyterLab のファイル |
| ai.py | 本記事で更新した ai_new.py |
| util.py | 本記事で更新した util_new.py |
次回の記事
更新履歴
| 更新日時 | 更新内容 |
|---|---|
| 2025/08/07 | PV を計算するプログラムの最後の if 文の else の部分が間違っていた点を修正しました |