目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義。現在は gui_play のみ定義されている |
| tree.py | ゲーム木に関する Node、Mbtree クラスの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
今回の記事の内容
αβ 法 は かなりわかりづらい アルゴリズムです。以前の記事で αβ 法について説明しましたが、Mbtree_Anim の実装がかなり長くなってしまったため、αβ 法について忘れてしまった方が多いのではないかと思いますので おさらい と まとめ をすることにします。また、ちゃんと説明していない点がある 事に気が付きましたのでその説明を行うことにします。
前回までの記事で αβ 法で評価値を計算する手順をアニーメーションで視覚化するための Mbtree_Anim を改良 してきたのは、αβ 法で行われる 処理を視覚化 することで わかりやすく確認できる ようにするためです。今回の記事では αβ 法のおさらいとまとめを行った後で、Mbtree_Anim を使って αβ 法で行われる処理を視覚的に確認する ことにします。
用語の定義
αβ 法 では 評価値を計算したいノード を ルートノード とするゲーム木の 部分木のノードに対する計算 を行います。そこで、本記事では以後は αβ 法で評価値を計算したいノード の事を単に ルートノード と表記することにします。
αβ 法のおさらいとまとめ
αβ 法 は ミニマックス法を改良 したアルゴリズムです。具体的には以前の記事で説明した下記のような処理を行うアルゴリズムで、枝狩り によって 一部のノードの処理を省略する ことで 処理時間を短くする という改良を行っています。
αβ 法は、ミニマックス法で評価値を計算する際 に、下記の手順で α 狩り と β 狩り を行うアルゴリズムである。また、αβ 法 で求められる評価値は、ミニマックス法 で求められる評価値と 常に同じ になるので、最適解 の評価値を ミニマックス法より短い時間 で 求めることができる。
-
min ノード では、下記の手順で α 狩り を行う
- 祖先ノード の中の max ノード をすべて探す
- 探した max ノードの中で、評価値が計算済 の 子ノードの評価値の最大値を α とする
- 子ノードの中で α 以下 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
-
max ノード では、下記の手順で β 狩り を行う
- 祖先ノード の中の min ノード をすべて探す
- 探した min ノードの中で、評価値が計算済 の 子ノードの評価値の最小値を β とする
- 子ノードの中で β 以上 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
また、以前の記事で説明したように、上記の αβ 法を実装 する ai_abs や Mbtree クラスの calc_score_by_ab メソッドでは下記のような処理を行っています。
-
min ノード
- 親ノードの β 値を初期値 として子ノードの評価値の 最小値 の計算を行う
- β 値 を計算した 最小値で更新 する。その結果 β 値が min ノードの評価値 となる
- 祖先ノードの max ノード の中の α 値の最大値 を利用して α 狩り を行う
-
max ノード
- 親ノードの α 値を初期値 として、子ノードの評価値の 最大値 の計算を行う
- α 値 を計算した 最大値で更新 する。その結果 α 値が max ノードの評価値 となる
- 祖先ノードの min ノード の中の β 値の最小値 を利用して β 狩り を行う
- 親ノードの α 値と β 値を子ノードの処理に伝える
αβ 法とミニマックス法の違い
αβ 法とミニマックス法と 比較するため に、下記にミニマックス法で行う処理を示します。
-
min ノード
- 子ノードの評価値の最小値の計算を行う
-
max ノード
- 子ノードの評価値の最大値の計算を行う
αβ 法 は以下の 4 点が ミニマックス法と異なります。この 4 つの処理 の意味が 直観的にわかりづらい ことが αβ 法がわかりづらい理由だと思います。
- α 値や β 値を初期値 として子ノードの評価値の最小値や最大値の計算を行う
- α 値や β 値を上記の 1 で計算した値で更新 し、そのノードの評価値とする
- α 狩りと β 狩り に関する処理を行う
- α 値と β 値 を 子ノードの処理に伝える
上記のうちの 1、2、4 については、以前の記事で説明したように 子ノードに祖先ノードの max ノードの子ノードの評価値の最大値と、min ノードの子ノードの評価値の最小値を 伝えるため に行っています。簡単にまとめると下記の理由で 子ノードに伝えられた α 値 には 祖先ノードの max ノード で計算された子ノードの 評価値の最大値が代入 されます。β 値に関しても同様です。
- α 値の初期値は負の無限大である
- α 値 は max ノードでのみ更新 される
- max ノード では 子ノードの評価値が α 値より大きい場合 に α 値を その値で更新 する
- α 値は子ノードの評価値を計算する際に、そのままの値 が子ノードの処理に 伝えられる
- 従って α 値には max ノード で計算された子ノードの 評価値の中の最大値が記録 される
上記の 3 の α 狩りと β 狩り を行って良い理由については以前の記事で詳しく説明したので忘れた方はそちらを復習して下さい。min ノードで α 狩りを行って良い理由 を簡単にまとめると以下のようになります。β 狩りについても同様です。
- min ノード で計算した子ノードの評価値が α 値以下になった場合 は、そのノードの評価値が α 以下 になることが確定する
- 以前の記事で説明した理由から、min ノードの評価値が α 以下の場合は 祖先ノードの max ノードの評価値の計算 に 影響を与えない
- αβ 法で 評価値を求めたいノード は 最も祖先のノード である ルートノード である
- αβ 法では 子ノードの評価値を利用 して 親ノードの評価値を計算 するので、min ノードの評価値が α 以下の場合は ルートノードの評価値に影響を与えない
- 従って、min ノードで計算した子ノードの評価値が α 値以下になった時点で 残りの子ノードの評価値の計算 を行う 意味がなくなる ので、α 狩りを行っても良い
α 値や β 値を初期値として計算を行って良い理由
ところで、α 値や β 値を初期値 として 子ノードの評価値を計算 する点に 疑問を感じた人 はいないでしょうか?
max ノード の子ノードの評価値の 最大値を M とした場合に、α < M であれば α 値は M に更新される ため、max ノードの評価値として ミニマックス法と同様 に子ノードの評価値の最大値である M が計算 されます。なお、α = M の場合は α 値は更新されませんが、ミニマックス法と 同じ値である M が計算 されます。
一方、そうでない M < α の場合は α 値は更新されない ため、αβ 法 で max ノードの評価値として計算された α 値と、ミニマックス法の場合に計算される max ノードの子ノードの評価値の最大値である M が異なる ことになってしまいます。
例えば max ノード で親ノードから伝えられた α 値が 0 の場合 で、全ての子ノードの評価値が -1 の場合は、そのノードの評価値 は ミニマックス法 では -1 が計算 されますが、αβ 法では α 値を初期値として計算するため 0 が計算 されます。具体例についてはこの後で Mbtree_Anim を利用して図で示すのでこちらのリンク先を見て下さい。
このことから、αβ 法 ではすべてのノードで正しい評価値を計算するミニマックス法と異なり、正しくない評価値が計算 される ノードが存在する可能性がある ことがわかります。
従って、αβ 法 を利用する際には 下記の性質がある点に注意する必要 があります。
αβ 法 で評価値を求めた際に、ルートノード以外のノード では 正しい評価値が計算されない場合がある。
正しくない評価値が計算されるノードが存在するにも関わらず、αβ 法では ルートノードの評価値は常に正しい値が計算 されます。その理由について少し考えてみて下さい。
α 値と β 値の性質は正反対 です。従って、α 値を初期値としても良い理由と、β 値を初期値としても良い 理由はほぼ同じ なので max ノードで α 値を初期値としても良い理由についてのみ説明することにします。
ルートノードの場合
評価値を計算するルートノードでは、α 値は負の無限大、β 値は正の無限大になります。従って、ルートノード が max ノードの場合は ミニマックス法と同様 に必ず子ノードの評価値の最大値が計算されるので、ルートノードの評価値は ミニマックス法の評価値と同じになります。ルートノードが min ノードの場合も同様です。
ルートノード以外の場合
max ノード の子ノードの評価値の 本当の最大値を M と表記した場合に、max ノードの評価値 が αβ 法とミニマックス法で 異なる のは、先程説明したように M < α の場合です。
その場合は、max ノードの評価値 として α 値 と M の どちらをを計算しても 以下の理由から ルートノードの評価値の計算に影響を与えません。これが α 値を初期値として max ノードの子ノードの評価値の最大値を計算しても 問題がない理由 です。
- max ノードの 親ノード は子ノードの評価値の 最小値を計算する min ノード である
- 従って、max ノードの評価値の計算結果 が親ノードから伝えられた α 値以下 の場合は、親ノードである min ノードの評価値 が必ず α 値以下 になる
- その場合は、親ノードで α 狩りが行われる ため ルートノードの評価値に影響を与えない
- M < α なので、max ノードの評価値として α 値 と M の どちらをを計算しても ルートノードの評価値に 影響を与えない
また、max ノードの評価値として α 値と M のどちらを計算しても構わないにも関わらず、実際には α 値を初期値として評価値を計算する理由 は以下の通りです。
- max ノードの子ノードの評価値の最大値である M を求めるため には 初期値を負の無限大 とする、α 値を記録する変数とは 別の変数を用意する必要 がある
- max ノードの子ノードの評価値を求める際に、子ノードに伝えるのはそれまでに計算した その max ノードだけ の子ノードの評価値の 最大値ではなく、祖先ノードの max ノードも含めた max ノードの子ノードの評価値の最大値である α 値 のほうである
- 従って α 値を初期値として計算する必要がある
- 一方、max ノードの評価しとして α 値と M のどちらを計算しても ルートノードの評価値の計算結果は変わらない ので、わざわざ M を計算する必要なない
α 値と β 値の意味
以前の記事で α 値と β 値の意味を下記のように説明しました。
α 値と β 値 は、ミニマックス法でそれぞれのノードの評価値を計算する際に、そのノードの評価値が 最終的に求める評価値 に 影響を与える可能性がない ことを表す 子ノードの評価値の範囲 を表す。
今回の記事の内容を踏まえて もう少し詳しく説明 すると以下のようになります。
- α 値と β 値は、子ノードの評価値 が α 値以下または β 値以上 の場合に ルートノードの評価値に影響を与えない ことを表す値である。従って、子ノードの評価値がその範囲で計算された場合は、その子ノードの評価値は 無視しても構わない
- 逆に言えば、子ノードの評価値が α 値と β 値の間 にある場合は、ルートノードの評価値に影響を与える可能性がある ため 無視することができない ことを意味する。ただし、必ず影響を与えるとは限らない1点に注意が必要である
- α 値以下 と、β 値以上 はいずれもルートノードの評価値に 影響を与えない範囲 であるが、以下の点で その意味が異なる
- max ノード では子ノードの評価値の 最大値を求める ため、子ノードの評価値が α 値以下 になった場合に 無視して良いのはその子ノードの評価値だけ である。従って、残りの子ノードの評価値の計算を 省略することはできない
- 一方 max ノードで子ノードの評価値が β 以上 になった場合はそのノードの評価値が β 以上になることが確定 するので、残りの子ノードの評価値の 計算を省略 するという β 狩りを行うことができる
- min ノードでは α 値と β 値が逆になる点を除いて同様である
Mbtree_Anim を利用した αβ 法の処理の確認
上記のような 言葉での説明だけではわかりづらい と思いますので、Mbtree_Anim を利用して αβ 法が行う処理を 視覚化して確認する ことにします。
αβ 法は 深さ優先アルゴリズム で処理を行うため、行う処理は下記の 3 種類に分類 されるので、それぞれで行われる処理について、Mbtree_Anim を利用して確認します。
- 次の子ノードの評価値を計算する処理を開始する
- 子ノードの評価値が得られた際に、その評価値の値に応じて α 値または β 値の更新、枝狩り、評価値の確定などの処理を行う
- 自身のノードの評価値が確定した際に、その評価値を親ノードに伝える
次の子ノードの評価値を計算する処理の開始の確認
αβ 法では、子ノードの評価値を計算する処理 を開始する際に、それまでに計算した α 値と β 値を子ノードの処理に伝える 必要があります。そこで、その処理が行われていること を Mbtree_Anim で確認 することにします。
なお、前回の記事までは 決着がついた局面の評価値 として -1 ~ 1 の範囲を計算 していましたが、評価値の範囲を広げたほうがわかりやすくなる と思いましたので、今回の記事では以前の記事で紹介した できるだけ早く勝利する着手を行う 以下の表のように -2 ~ 3 の範囲 で決着がついた局面の評価値を計算することにします。
| 局面の深さ | 5 | 6 | 7 | 8 | 9 | 評価値の計算式 |
|---|---|---|---|---|---|---|
| 〇 が勝利した場合の評価値 | 3 | 2 | 1 | (11 - 局面の深さ)÷ 2 | ||
| × が勝利した場合の評価値 | -2 | -1 | (局面の深さ - 10)÷ 2 |
αβ 法で評価値を計算する calc_score_by_ab では、決着がついた局面の評価値 を下記の calc_score_of_node メソッドで計算しており、このメソッドでは 3、7 行目のように、shortest_victory 属性が True の場合に上記の表の評価値を計算します。
1 def calc_score_of_node(self, node:Node):
2 if node.mb.status == Marubatsu.CIRCLE:
3 node.score = (11 - node.depth) / 2 if self.shortest_victory else 1
4 elif node.mb.status == Marubatsu.DRAW:
5 node.score = 0
6 elif node.mb.status == Marubatsu.CROSS:
7 node.score = (node.depth - 10) / 2 if self.shortest_victory else -1
8 node.max_score = node.score
9 node.min_score = node.score
従って、下記のプログラムを実行することで、上記の表の評価値で αβ 法による評価値を計算することができます。
from tree import Mbtree, Mbtree_Anim
mbtree = Mbtree(algo="df", shortest_victory=True)
mbtree.calc_score_by_ab(mbtree.root)
Mbtree_Anim(mbtree, isscore=True)
ルートノードからの処理の確認
まず、ルートノードの最初の子ノード の評価値を計算する処理を開始する際の α 値と β 値を確認 します。
下図左は ルートノードの処理が開始 された 0 フレーム目、下図右はその 最初の子ノードの処理が開始 された 1 フレーム目の図です。αβ 法の処理が開始 された時点では α 値は負の無限大、β 値は正の無限大 で、子ノードの処理が開始された際に α 値と β 値が変化せずにそのまま伝わっている ことが確認できます。
下図はその後の 2 フレーム目、3 フレーム目の図です。αβ 法は 深さ優先アルゴリズム なので、次々に最初の子ノードの処理が開始 されていますが、その際にいずれも α 値と β 値がが変化せずにそのまま伝わっている ことが確認できます。
他のノードでの確認
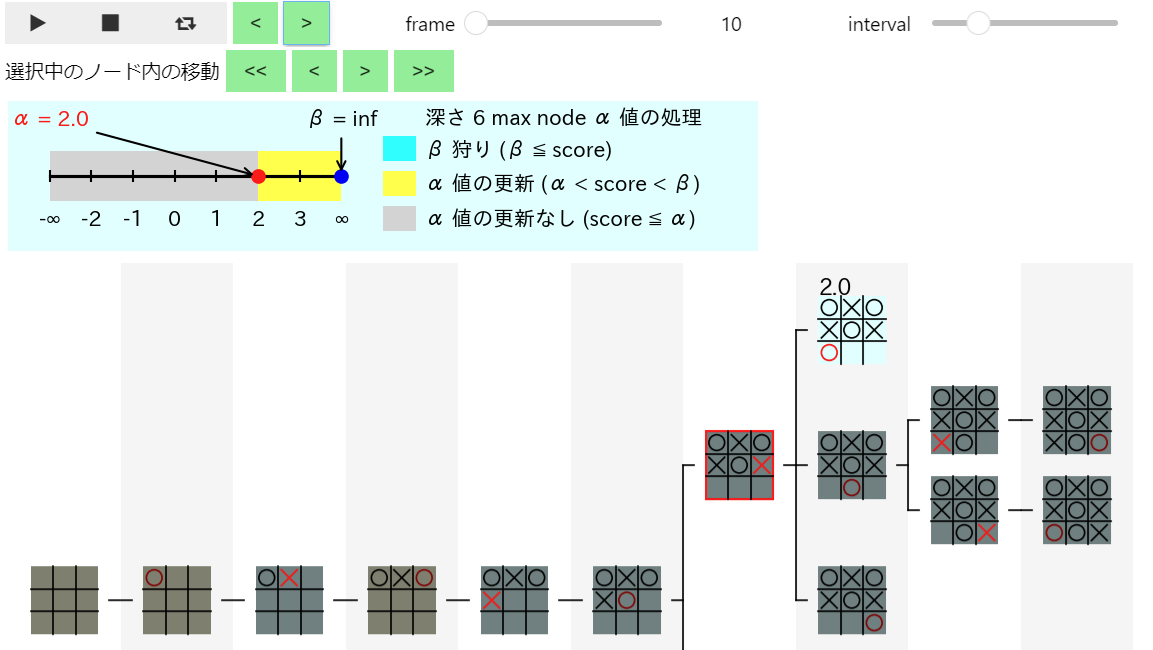
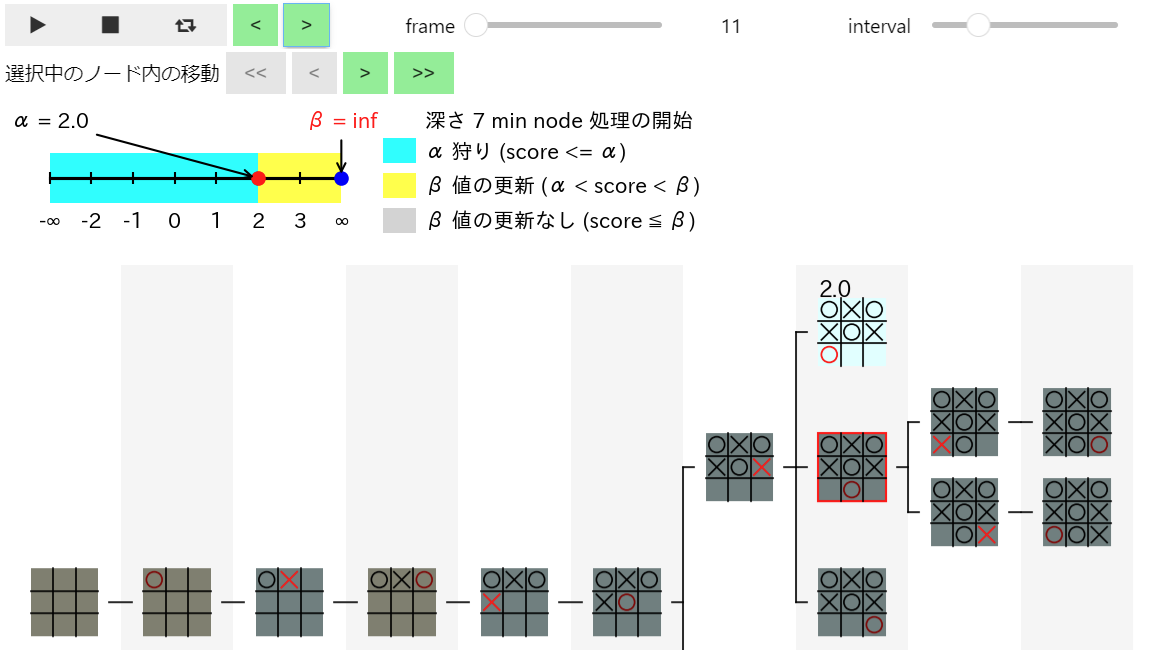
下図は赤枠の最初の子ノードの評価値を計算した結果 α 値が 2 に更新 された 10 フレーム目の図と、赤枠の 次の子ノードの処理が開始 された 11 フレーム目の図です。この場合でも、α 値と β 値がが変化せずにそのまま伝わっている ことが確認できます。
下図は赤枠のノードの α 値が 0、β 値が 2 の場合の 50 フレーム目の図と、赤枠の 次の子ノードの処理が開始 された 51 フレーム目の図です。この場合でも、α 値と β 値がが変化せずにそのまま伝わっている ことが確認できます。
なお、上図と下図の両方で共通しますが、min ノードと max ノードで 枝狩りを行う範囲 が α 値以下と、β 値以上で 異なる ので、水色と灰色の部分が前後の図で入れ替わります。


上記から、以下の事が確認できました。
αβ 法で、次の子ノードの評価値を計算する処理を開始 する際には、α 値と β 値 は変化せずに そのまま子ノードの処理に伝えられる。
評価値を親ノードに伝える処理の確認
先に比較的簡単に説明できる、自身のノードの評価値が確定した際にその 評価値を親ノードに伝える処理の確認 を行います。
下図左は赤枠のノードの 評価値が確定 した 11150 フレーム目、下図右はその 評価値が親ノードに伝わった 11151 フレーム目の図です。
左図の β 値 が 右図では score になり、β 値が負の無限大に変化 しています。α 値と β 値は、親ノードから子ノードにそのまま受け継がれるので、お互いのノードが α 値と β 値を共有しているように見えるため、上記のように β 値が変化する点に戸惑う 人がいるかもしれませんが、以下のような理由で β 値が変化します。
- α 値と β 値 は それぞれのノードが独自に持つ値 であり、特定のノードの α 値や β 値を変更しても、他のノードの α 値や β 値が変更されることはない
- 従って、子ノードの処理によって 子ノードの α 値や β 値を変更 しても、親ノードの α 値や β 値の値 は 変更されない
左図の β 値は赤枠のノードの評価値を計算した結果 0 に更新された値で、その更新によって 親ノードの β 値が直接更新されることはありません2。右図の β 値は左図の赤枠のノードの評価値を計算する処理が行われる前の値です。
α 値と β 値 の値は、それぞれのノードで 独立して記録 されている。そのため、子ノードの α 値や β 値の更新は、親ノードの α 値や β 値に 直接影響を与えない。
子ノードの評価値が得られた場合の処理の確認
max ノード で子ノードの評価値が得られた場合に行われる処理は「β 狩り が行われる」、「β 狩りが行われずに α 値が更新される」、「α 値が更新されない」の 3 種類なので、それぞれの処理確認することにします。なお、max ノードと min ノードで行われる処理は良く似ているので、max ノードでの処理の説明を詳しく行います。
max ノードで枝狩りが行われずに α 値が更新される場合
まず、max ノードの評価値を計算する際に、枝狩りが行われず に α 値が更新される 場合の処理を確認します。下図の 2 フレーム目の 赤枠のノードは max ノード です。この時点では赤枠の 祖先ノード の max ノードと min ノードの中で 評価値が計算されている子ノードは存在しない ので α 値は負の無限大、β 値は正の無限大 になっています。

前回の記事で作成した > ボタンなどで赤枠のノードに対する処理が行われたフレームを表示し、それぞれのフレームの α 値と β 値の図 を 順に並べる と以下の表ようになります。
| α 値と β 値の図 | |
|---|---|
| 開始時 |  |
 |
 |
| α 値の更新3 |  |
 |
 |
| α 値の更新 |  |
 |
 |
| α 値の更新なし |  |
| 4 ~ 7 番目の子ノードの評価値はいずれも 2 で 上記と同じで α 値の更新は行われないので省略 |
|
| 評価値の確定 |  |
max ノード の評価値を計算する際に、β 狩りが行われず に α 値が更新される 場合は、上記の表から以下のような計算が行われることがわかります。
- α 値 には 子ノードの評価値 のうちの 最大値が計算 されるので、α 値 にはミニマックス法と同様に max ノードの評価値が計算 される
- β 値 は 変更されない
そのことは上図で α 値 が 左から右に更新されていく様子 から確認することができます。
図は省略しますが、min ノード では β 値が更新される場合 は、必ず 右から左に更新 されます。興味がある方は Mbtree_Anim で実際に確認してみて下さい。
なお、上記では処理を開始する際の α 値と β 値の初期値はそれぞれ負の無限大と正の無限大ですが、α 値と β 値の初期値が別の値 であっても、上記と同じ ことが言えます。
さらに、α 値の更新が行われない場合 でも、α 値と同じ値の評価値 の子ノードが 存在した場合 は、α 値 が子ノードの評価値の 最大値となる ので 上記と同じ ことが言えます。
上記をまとめると以下のようになります。
max ノード では以下の条件が満たされる場合は、αβ 法によって計算される α 値 はミニマックス法が計算する子ノードの 評価値の最大値と同じ値 になる。
- 子ノードの評価値の最大値 が α 以上 β 未満 である
max ノードですべての子ノードの評価値が α 未満の場合
下図は赤枠のノードの評価値の計算を開始するフレームの図で、α 値の初期値は 0、β 値の初期値は正の無限大 になっています。

上図の赤枠のノードに対する処理が行われたそれぞれのフレームの α 値と β 値の図を順に並べると以下の表のようになります。
| α 値と β 値の図 | |
|---|---|
| 開始時 |  |
 |
 |
| α 値の更新なし |  |
 
|
2、3 番目の子ノードの評価値はいずれも -1 で 上記と同じ図になるので省略 |
| 評価値の確定 |  |
上記の場合は、子ノードの 評価値の最大値は -1 になるため、ミニマックス法 では赤枠のノードの 評価値は -1 になりますが、αβ 法 では α 値が max ノードの評価値として計算 されるので赤枠のノードの 評価値は 0 になります。先程説明したように、max ノード の すべての子ノードの評価値 が α 値よりも小さい場合 は、αβ 法で計算した評価値 α はそのノードの 本当の評価値より大きな、異なる値 になることが実際に確認できました。
このような場合でも ルートノードの評価値が正しく計算される理由 については、先程説明した通りです。
β 狩りが行われる場合
下図は赤枠のノードの評価値の計算を開始するフレームの図で、α 値の初期値 は 負の無限大、β 値の初期値 は 2 になっています。

上図の赤枠のノードに対する処理が行われたそれぞれのフレームの α 値と β 値の図を順に並べると以下のようになります。
| α 値と β 値の図 | |
|---|---|
| 開始時 |  |
 |
 |
| α 値の更新 |  |
 |
 |
| β 狩り |  |
| 評価値の確定 |  |
下図は β 狩りが行われた結果、枝狩りが行われたノードが暗い色で描画されるようになった図です。

max ノードの 親ノードは min ノードで、min ノードでは 子ノードの評価値が β 値よりも小さい場合に更新する ので、β 値以上である α 値 を max ノードの 評価値として計算しても、親ノードである min ノードではその値は β 値の更新には使われません。
β 狩りを行っても良い理由についてのより詳しい説明は、以前の記事を復習して下さい。
max ノードと min ノードで行われる処理のまとめ
max ノードで行われる処理は、大きくなるという条件 で α 値 を 子ノードの評価値の値で更新 し、β 値以上 になった時点で β 狩りを行う というものです。
また、α 値と β 値の図で 色分けされた評価値の範囲の性質 は以下のようになります
- 灰色の範囲 は 祖先ノードの max ノード の評価値である α 値の計算 に 影響を与えない ため、ルートノードの評価値に影響を与えないので 無視して良い 範囲
- 黄色の部分 は祖先ノードの max ノードの評価値の計算に 影響を与える可能性がある範囲
- 水色の部分 は 親ノードの min ノード の評価値である β 値の計算に 影響を与えないことが確定 するため、それ以降 の子ノードの評価値の計算を 省略して良い範囲
min ノード は max ノードと 正反対の性質を持つ ため、行われる処理も max での処理の反対 です。そのため、図を用いた説明は省略し、処理のまとめのみを以下に説明します。興味がある方は、Mbtree_Anim を利用して min ノードで行われる処理を確認してみて下さい。
min ノードで行われる処理は、β 値が小さくなる ように子ノードの評価値の値で 更新 し、α 値以上 になった時点で α 狩りを行う というものです。
また、α 値と β 値の図で 色分けされた評価値の範囲の性質 は max ノードと同様 です。
αβ 法で行われる処理のまとめ
Mbtree_Anim で行われる処理を 観察する ことで、αβ 法では、子ノードの評価値を計算するたび に、α 値と β 値の図の範囲 によって以下の処理を行うことが確認できます。また、この表から、α 値と β 値 は ルートノード の評価値に対して 3 種類の影響 を与える子ノードの評価値の 範囲の境目 を表していることがわかります。
| 範囲 | 意味 |
|---|---|
| 灰色 | その子ノードの評価値が、ルートノードの評価値の計算 に 影響を与えない範囲。残りの 子ノードの評価値の 計算は続行 する |
| 黄色 | その子ノードの評価値が、ルートノードの評価値の計算に 影響を与える可能性がある範囲。α 値または β 値を更新して 黄色の範囲を狭め、残り の子ノードの評価値の 計算を続行 する |
| 水色 | その子ノードと残りの子ノード の評価値が、ルートノードの評価値の計算に 影響を与えない範囲。枝狩りを行って 残りの子ノードの評価値の 計算を省略する |
また、上記の範囲に注目 することで、α 値と β 値が以下のような性質を持つことが観察できました。
- α 値と β 値は 子ノードの評価値を計算する際 に、そのまま受け継がれる
- α 値 は max ノード では 黄色い範囲を狭める ように図では 右方向に増加 するか、変化しない という性質がある
- α 値が増える と、子孫ノードの min ノードで α 狩り を行う 水色の範囲が増える
- α 値 は min ノード では 変化しない
- β 値 は min ノード では 黄色い範囲を狭める ように図では 左方向に減少 するか、変化しない という性質がある
- β 値が減る と、子孫ノードの max ノードで β 狩り を行う 水色の範囲が増える
- β 値 は max ノード では 変化しない
このことから、祖先ノード で 子ノードの評価値が多く計算されるほど、その 評価値の情報によって 枝狩りを行う 水色の範囲が広がっていく ことになるため、枝狩りが行われやすくなる ことがわかります。
例えば、今回の記事の最初で行った、ルートノードからの処理の確認では、子ノードの評価値が全く計算されない ため、α 値と β 値は変化しません。
一方、子ノードの評価値が計算 されると α 値と β 値が更新 され、黄色の範囲が狭まる ことで、子ノードでの枝狩りが行われやすく なります。例えば、今回の記事の max ノードで枝狩りが行われずに α 値が更新される場合では、下記の表のように 1 つ目と 2 つ目の子ノードの評価値が計算されると α 値が右方向に更新 されて 黄色の範囲が狭くなります。
| α 値と β 値の図 | |
|---|---|
| 開始時 |  |
 |
 |
| α 値の更新 |  |
 |
 |
| α 値の更新 |  |
下図左は上記の 2 つ目の子ノードの評価値の計算を開始するフレームで、下図右は 3 つ目の子ノードの評価値の計算を開始するフレームです。図から 右図の方が α 狩りを行う水色の範囲が広がっている ため 枝狩りが行われやすくなっている ことが確認できます。
下図左は、上図右の最初の子ノードの評価値が計算されたフレームで、その右は 2 つ目の子ノードの評価値の計算を開始するフレームです。図からわかるように β 値が計算 されたことによって、黄色の範囲がさらに狭く なり、max ノードでの水色の範囲が増えている ことが確認できます。
今回の記事のまとめ
今回の記事では、αβ 法についてのおさらいとまとめ を行い、Mbtree_Anim を利用して、αβ 法が行う処理の確認と説明 を行いました。今回の説明でもまだピンとこない人がいるかもしれませんが、Mbtree_Anim によって αβ 法の理解につながるのであれば幸いです。
本記事で入力したプログラム
| リンク | 説明 |
|---|---|
| marubatsu.ipynb | 本記事で入力して実行した JupyterLab のファイル |
次回の記事









