目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義。現在は gui_play のみ定義されている |
| tree.py | ゲーム木に関する Node、Mbtree クラスの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
バグの原因の検証と修正
前回の記事では、引き分けの局面の最善手に対して、下記のような方法で優劣をつけたゲーム木の評価値を計算しました。
-
× の手番の局面の場合
- 相手の着手によって 〇 が 勝利する可能性がある 場合は 0.5
- そうでない場合は 0
-
〇 の手番の局面の場合
- 相手の着手によって × が 勝利する可能性がある 場合は -0.5
- そうでない場合は 0
前回の記事のバグのおさらい
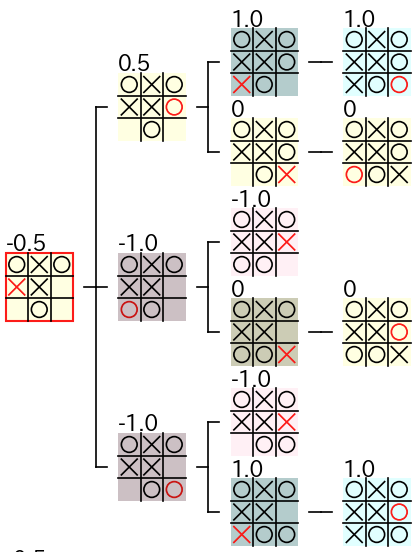
しかし、計算した評価値を利用して Marubatsu_GUI クラスでゲーム木を表示すると、下図のように深さが 2、4、6 の 〇 の手番の引き分けの局面 に 0.5 という評価値が計算 されていることがわかります。先ほど説明した評価値の計算では、〇 の手番の引き分けの局面 の評価値は 0 または -0.5 のいずれかになるので、この評価値は間違っています。

また、上図の深さ 5 の × の手番の一番上のノードをクリックすると下図のような部分木が表示されます。図から、(0, 1)、(2, 1) に着手した局面には子孫ノードに × が勝利するノードが存在 し、(0, 2)、(2, 2) に着手した場合は × が勝利するノードが 存在しない ので、この局面の 最善手は (0, 1) と (2, 1) になるはず ですが、図のように合法手の局面の 評価値が全て 0.5 になっているため、全ての合法手が最善手 になるという 間違いが発生 しています。

バグの原因の検証
評価値がおかしい ので、評価値を計算する処理を行う下記の calc_score_by_bf を検証することにします。
1 def calc_score_by_bf(self):
略
2 if node.mb.status != Marubatsu.PLAYING:
3 self.calc_score_of_node(node)
4 else:
5 score_list = [childnode.score for childnode in node.children]
6 if node.mb.move_count % 2 == 0:
7 score = max(score_list)
8 else:
9 score = min(score_list)
10 node.score = score
11 node.max_score = max([childnode.max_score for childnode in node.children])
12 node.min_score = min([childnode.min_score for childnode in node.children])
13 if node.score == 0:
14 if node.mb.move_count % 2 == 1:
15 if node.max_score > 0:
16 node.score = 0.5
17 else:
18 if node.min_score < 0:
19 node.score = -0.5
略
上記のプログラムでは、4 ~ 10 行目 で ミニマックス法 によって 子ノードの評価値の最大値(または最小値)を計算 し、それを自身のノードの 評価値(score 属性)として計算 しています。その後の 11、12 行目 でこのノードの 最大の評価値(max_score 属性) と 最小の評価値(min_score 属性)を計算 しています。
また、その後の 13 行目で自身のノードの評価値が引き分けの局面を表す 0 の場合に、14 ~ 19 行目 で 引き分けの局面に優劣をつける ために 評価値(score 属性)の値を修正する処理 を行っています。
下記は、先程の間違った評価値が計算されたゲーム木の一部です。赤枠 の 〇 の手番の 引き分けの局面 ノードの評価値は、子孫ノードに 〇 が勝利するノードが存在 するので 本当は -0.5 と計算 されるはずが、0.5 と計算されている点が間違っています。そこで、赤枠のノードの評価値がどのように間違って計算されるかについて検証することにします。

深さが 9 のノードの評価値の計算
ミニマックス法 では、ノードの評価値を 子ノードの評価値を使って計算する ので、赤枠の深さが 6 のノードの評価値を計算するためには、深さが 9、8、7 のノードの評価値を 順に計算する 必要があります。
上図の右端の 深さが 9 のノード は、すべて 決着がついた局面 であり、その場合の評価値は以前の記事で説明した下記の表のように計算します。この表から上図の 深さ 9 のノード に表示される 評価値が正しく計算されている ことが確認できます。
| 局面の深さ | 5 | 6 | 7 | 8 | 9 | 評価値の計算式 |
|---|---|---|---|---|---|---|
| 〇 が勝利した場合の評価値 | 3 | 2 | 1 | (11 - 局面の深さ)÷ 2 | ||
| × が勝利した場合の評価値 | -2 | -1 | (局面の深さ - 10)÷ 2 |
また、決着がついたノードの最大の評価値と最小の評価値は、calc_score_of_node で下記のプログラムのように、そのノードの 評価値と同じ値が計算 されます。
def calc_score_of_node(self, node:Node):
略
node.max_score = node.score
node.min_score = node.score
上記から、以下の事が確認できました。
- 上図の 深さが 9 のノードの評価値 は 正しい値が計算 されている
- 深さが 9 のノードの 最大の評価値 と 最小の評価値 は、評価値と同じ値が計算 される
深さが 8 のノードの評価値の計算
下図の右から 2 列目の 深さが 8 のノード のうち、上から 3 番目 と 5 番目 のノードは × の勝利で決着がついている局面 なので、上記と同様の方法で評価値を計算すると -1 が計算 されます。従って、下図ではそれらのノードに対して 評価値が正しく計算されている ことが確認できます。また、最大の評価値、最小の評価値 は、評価値と同じ -1 が計算 されます。

次に、深さが 8 のノードの中で、残りの 子ノードを持つノードの評価値 の計算を検証します。深さが 8 のノードは 〇 の手番 のノードなので、ミニマックス法では 子ノードの評価値の最大値 がそのノードの評価値として計算されますが、深さが 8 のノードの中で子ノードが存在するノードには、子ノードは 1 つしか存在しません。そのためその評価値は 子ノードの評価値と同じ になります。
また、最大の評価値 と 最小の評価値 は、子ノードの評価値の最大値または最小値で計算されますが、同様の理由 で 子ノード の最大の評価値と最小の評価値 と同じ になります。
上図の深さ 8 のノードの上から 1、2、4、6 番のノードにはそのような評価値が表示されているので、正しい評価値が計算されている ことが確認できます。
ミニマックス法の後 で 引き分けの局面の評価値 が 0.5 や -0.5 に 変更される のは、最大の評価値 や 最小の評価値 が 0 でない場合 ですが、上図の深さ 8 の 2、4 番目の引き分けの局面のノードは その条件に当てはまらない ので 評価値は 0 のまま 変更されません。
上記の事から、以下の事が確認できました。
- 上図の 深さが 8 のノードの評価値 は 正しい値が計算 されている
- 深さが 8 のノードの 最大の評価値 と 最小の評価値 は、評価値と同じ値 が計算される
深さが 7 のノードの評価値の計算
下図の左から 2 列目の 深さが 7 のノード の中に決着がついている局面は存在しません。また、深さが 7 のノードは × の手番の局面 なので、ミニマックス法 では 子ノードの評価値の最小値 がそのノードの評価値として計算されます。また、最大の評価値と最小の評価値は、子ノードの評価値の最大値と最小値で計算されます。

下記は、深さが 7 のノードの評価値、最大の評価値、最小の評価値の計算結果です。
| 評価値 | 最大の評価値 | 最小の評価値 | |
|---|---|---|---|
| 1 つ目 | 0 |
1 |
0 |
| 2 つ目 | -1 |
0 |
-1 |
| 3 つ目 | -1 |
1 |
-1 |
× の手番 の 引き分けの局面の評価値 は、子孫ノード の中に 〇 が勝利する局面が存在する場合 は 0.5 と計算する 必要があり、その処理は calc_score_by_bf の中の下記のプログラムで行われます。上記の表から、深さ 7 の 引き分けの局面 である 1 つ目のノードの 最大の評価値(max_score 属性)は 1 なので、その ノードの評価値は 0.5 に修正 されます。
if node.score == 0:
if node.mb.move_count % 2 == 1:
if node.max_score > 0:
node.score = 0.5
従って、深さ 7 のノードの評価値は下記の表のようになり、上図の深さが 7 のノード の評価値は 正しい値が計算されている ことが確認できました。
| 評価値 | 最大の評価値 | 最小の評価値 | |
|---|---|---|---|
| 1 つ目 | 0.5 |
1 |
0 |
| 2 つ目 | -1 |
0 |
-1 |
| 3 つ目 | -1 |
1 |
-1 |
赤枠の深さが 6 のノードの評価値の計算
下図の赤枠の 深さが 6 のノード は決着がついておらず、〇 の手番 の局面なので、ミニマックス法では 子ノードの評価値の最大値 がそのノードの評価値として計算されます。また、最大の評価値と最小の評価値は、子ノードの評価値の最大値と最小値で計算されます。

下記は、深さが 6 のノードの評価値、最大の評価値、最小の評価値の計算結果です。
| 評価値 | 最大の評価値 | 最小の評価値 |
|---|---|---|
0.5 |
1 |
-1 |
〇 の手番 の引き分けの局面の評価値は、子孫ノード の中に × が勝利する局面が存在する 場合は -0.5 と計算 する必要があり、その処理は calc_score_by_bf の中の下記のプログラムの 6 行目で行われます。
1 if node.score == 0:
2 if node.mb.move_count % 2 == 1:
3 略
4 else:
5 if node.min_score < 0:
6 node.score = -0.5
上記の 6 行目が実行されるため には、下記の条件を すべて満たす 必要があります。
- 評価値(
score属性)が引き分けの局面を表す0である - 手番が 〇 の局面(
move_count属性が偶数)である - 最小の評価値(
min_score属性)の値が負である
先程の表から上記の 2、3 番目の条件は満たされますが、評価値の値は 0.5 なので 1 番目の条件は満たされません。そのため、上記の 6 行目は実行されず、評価値 の値は 0.5 から変化しません。これが赤枠の局面の評価値が 0.5 という間違った値になる原因です。
この問題を修正する方法を少し考えてみて下さい。
今気づいたのですが、〇 の手番であることの判定は mb.turn == Marubatsu.CIRCLE で行えます。move_count が偶数であるかどうかで判定する方法はわかりにくいですが、今から過去のプログラムをさかのぼって修正するのは大変なので、既に記述した部分のプログラムでは引き続きこの方法で判定することにします。
calc_score_by_bf の修正
このプログラムの問題は、引き分けの局面の評価値 を 0 だけでなく、-0.5、0.5 に増やした にも関わらず、上記のプログラムの 1 行目 で 引き分けの局面であること を 評価値が 0 であることで判定 している点です。前回の記事で、ノードの色を計算する際に -1 < 評価値 < 1 の場合に 引き分けの局面である事を表すとした ので、それに合わせて calc_score_by_bf を下記のプログラムの 5 行目のように修正することで、このバグを修正することができます。
1 from tree import Mbtree
2 from marubatsu import Marubatsu
3
4 def calc_score_by_bf(self):
元と同じなので省略
5 if -1 < node.score < 1:
6 if node.mb.move_count % 2 == 1:
7 if node.max_score > 0:
8 node.score = 0.5
元と同じなので省略
9
10 Mbtree.calc_score_by_bf = calc_score_by_bf
行番号のないプログラム
from tree import Mbtree
from marubatsu import Marubatsu
def calc_score_by_bf(self):
self.nodelist_by_score = self.nodelist[:]
for nodelist in reversed(self.nodelist_by_depth):
for node in nodelist:
if node.mb.status != Marubatsu.PLAYING:
self.calc_score_of_node(node)
else:
score_list = [childnode.score for childnode in node.children]
if node.mb.move_count % 2 == 0:
score = max(score_list)
else:
score = min(score_list)
node.score = score
node.max_score = max([childnode.max_score for childnode in node.children])
node.min_score = min([childnode.min_score for childnode in node.children])
if -1 < node.score < 1:
if node.mb.move_count % 2 == 1:
if node.max_score > 0:
node.score = 0.5
else:
if node.min_score < 0:
node.score = -0.5
self.nodelist_by_score.append(node)
node.score_index = len(self.nodelist_by_score) - 1
Mbtree.calc_score_by_bf = calc_score_by_bf
修正箇所
from tree import Mbtree
from marubatsu import Marubatsu
def calc_score_by_bf(self):
元と同じなので省略
- if node.score == 0:
+ if -1 < node.score < 1:
if node.mb.move_count % 2 == 1:
if node.max_score > 0:
node.score = 0.5
else:
node.score = 0
元と同じなので省略
Mbtree.calc_score_by_bf = calc_score_by_bf
上記の修正後に下記のプログラムを実行すると、実行結果のように 〇 の手番 の深さが偶数のノードの 引き分けの局面の評価値 に -0.5 という正しい値が計算される ようになることが確認できます1。
from tree import Mbtree_GUI
mbtree = Mbtree(shortest_victory=True)
data = mbtree.calc_and_save_bestmoves_and_score_by_board("test.dat")
Mbtree_GUI(scoretable_dict={"test": data})
実行結果

また、先程の 検証で使った局面 を中心とする部分木を表示すると、左下図 のように 正しい評価値 である -0.5 が計算 されていることが確認できます。先ほどの間違った計算が行われていた右下図と比べてみて下さい。
これで、バグが修正されたと思った方がいるかもしれませんが、このプログラムには バグがまだ残っています。どのようなバグが存在するかについて少し考えてみて下さい。ヒントは、そのバグは 2 つ上の ルートノードを中心とした部分木の図の中 にあります。
バグとその検証
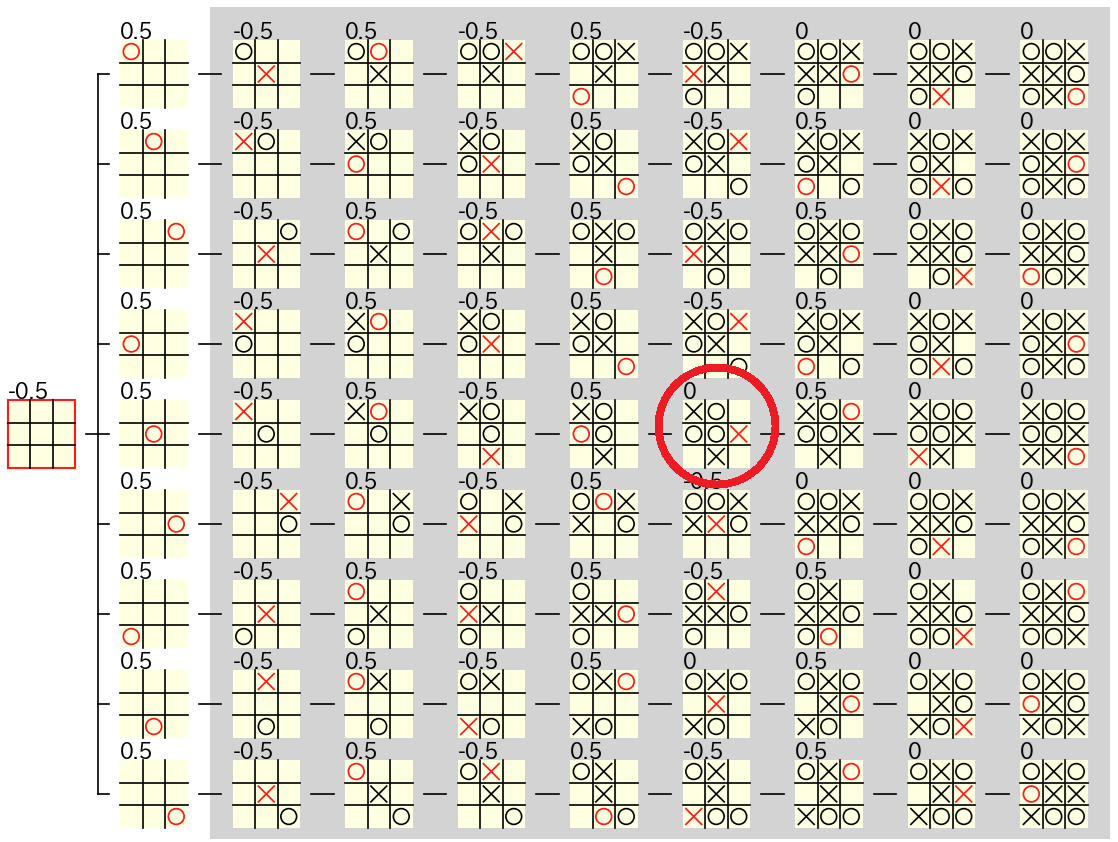
評価値が間違っているノードは 1 つしかないので この間違いに気づくことはかなり困難 ですが、問題は下図の 赤丸のノード にあります。このノードは 〇 の手番の局面 ですが評価値として 0.5 が計算 されている点が 間違っています。

下図はこのノードをクリックして表示される、このノードを中心とした部分木です。

先程と同じ手順で、このノードの子ノードである左から 2 列目の 深さが 7 のノードの評価値を計算すると、下記の表ようになります。
| 評価値 | 最大の評価値 | 最小の評価値 | |
|---|---|---|---|
| 1 つ目 | 0.5 |
1 |
0 |
| 2 つ目 | 0.5 |
1 |
0 |
| 3 つ目 | 0 |
0 |
0 |
下記の表は上記を元に 〇 の手番 である 赤枠のノードの評価値 を ミニマックス法で計算 した表です。
| 評価値 | 最大の評価値 | 最小の評価値 |
|---|---|---|
0.5 |
1 |
0 |
上記の計算結果に対して、引き分けの局面 での 優劣を表す評価値 を計算する下記のプログラムを実行すると、1 行目の条件式は True、2 行目の条件式は False、6 行目の条件式は False なので、下記のプログラムでは score 属性に対する処理は行われない ため、赤枠のノードの 評価値は 0.5 のまま変化しない ことになります。これが上記のバグの原因です。このバグを修正する方法について少し考えてみて下さい。
1 if -1 < node.score < 1:
2 if node.mb.move_count % 2 == 1:
3 if node.max_score > 0:
4 node.score = 0.5
5 else:
6 if node.min_score < 0:
7 node.score = -0.5
バグの修正
このバグを修正するためには、引き分けの局面 では 〇 の手番 の場合に 評価値を 0 か -0.5 のいずれかになるようにする必要があります。また、同様に × の手番 の場合に 評価値を 0 か 0.5 のいずれかになるようにする必要があります。下記は、そのように calc_score_by_bf を修正したプログラムです。
-
6、7 行目:× の手番の局面の場合に、評価値が
0.5でなければ、0にする -
11、12 行目:〇 の手番の局面の場合に、評価値が
-0.5でなければ0にする
1 def calc_score_by_bf(self):
元と同じなので省略
2 if -1 < node.score < 1:
3 if node.mb.move_count % 2 == 1:
4 if node.max_score > 0:
5 node.score = 0.5
6 else:
7 node.score = 0
8 else:
9 if node.min_score < 0:
10 node.score = -0.5
11 else:
12 node.score = 0
元と同じなので省略
13
14 Mbtree.calc_score_by_bf = calc_score_by_bf
行番号のないプログラム
def calc_score_by_bf(self):
self.nodelist_by_score = self.nodelist[:]
for nodelist in reversed(self.nodelist_by_depth):
for node in nodelist:
if node.mb.status != Marubatsu.PLAYING:
self.calc_score_of_node(node)
else:
score_list = [childnode.score for childnode in node.children]
if node.mb.move_count % 2 == 0:
score = max(score_list)
else:
score = min(score_list)
node.score = score
node.max_score = max([childnode.max_score for childnode in node.children])
node.min_score = min([childnode.min_score for childnode in node.children])
if -1 < node.score < 1:
if node.mb.move_count % 2 == 1:
if node.max_score > 0:
node.score = 0.5
else:
node.score = 0
else:
if node.min_score < 0:
node.score = -0.5
else:
node.score = 0
self.nodelist_by_score.append(node)
node.score_index = len(self.nodelist_by_score) - 1
Mbtree.calc_score_by_bf = calc_score_by_bf
修正箇所
def calc_score_by_bf(self):
元と同じなので省略
if -1 < node.score < 1:
if node.mb.move_count % 2 == 1:
if node.max_score > 0:
node.score = 0.5
+ else:
+ node.score = 0
else:
if node.min_score < 0:
node.score = -0.5
+ else:
+ node.score = 0
元と同じなので省略
Mbtree.calc_score_by_bf = calc_score_by_bf
上記の修正後に下記のプログラムを実行すると、実行結果のように 赤丸 の 〇 の手番の引き分けの局面の 評価値に 0 という正しい値が計算される ようになることが確認できます。
mbtree = Mbtree(shortest_victory=True)
data = mbtree.calc_and_save_bestmoves_and_score_by_board("test.dat")
Mbtree_GUI(scoretable_dict={"test": data})
実行結果
ミニマックス法と引き分けの局面の評価値の計算の分離
評価値を計算する calc_score_by_bf の中 に引き分けの局面の最善手に優劣をつける 評価値を計算する処理を記述した際 に、今回の記事で紹介したような 2 つのバグが発生した理由 は、ミニマックス法 で評価値を計算する処理と、ミニマックス法と異なる方法 で評価値を計算する 処理を混ぜてしまったから です。
このように 性質が異なる処理 を 無理にまとめて行おうとする と、正しい計算が行われない可能性が高くなる ので、特別な理由2がない限りは 避けたほうが無難 です。実際に、今回の記事で行った修正のように、正しい計算が行われるようにするために 別の処理を記述する必要 が生じたり、その分だけ プログラムがわかりづらくなる という欠点が生じます。また、今回の記事で紹介した 2 つ目のバグのように、見つけることが非常に困難なバグが発生する ことがあります。
引き分けの局面の最善手に優劣をつけるため の評価値の 計算の処理 を、ミニマックス法 による評価値の 計算が完全に終わった後 で行えばそのような 問題は発生しない ので、Mbtree クラスに下記のようなメソッドを定義する事にします。
処理:引き分けの局面の最善手に優劣をつけるための評価値を計算する
名前:評価値(score)を 再計算(recalculate)するので recalculate_score とする
入力:なし
出力:なし
今回の記事の最後で簡単に説明しますが、必敗の局面の最善手の優劣をつけたい場合は、必敗の局面の評価値を再計算する必要があります。そのような計算を行うことができるようにするために、メソッドの名前の中に draw を入れないようにしました。
Mbtree クラスの calc_score_by_bf の修正
まず、下記のプログラムのように、calc_score_by_bf から 引き分けの局面の評価値を修正する処理を削除 する必要があります。
def calc_score_by_bf(self):
self.nodelist_by_score = self.nodelist[:]
for nodelist in reversed(self.nodelist_by_depth):
for node in nodelist:
if node.mb.status != Marubatsu.PLAYING:
self.calc_score_of_node(node)
else:
score_list = [childnode.score for childnode in node.children]
if node.mb.move_count % 2 == 0:
score = max(score_list)
else:
score = min(score_list)
node.score = score
node.max_score = max([childnode.max_score for childnode in node.children])
node.min_score = min([childnode.min_score for childnode in node.children])
self.nodelist_by_score.append(node)
node.score_index = len(self.nodelist_by_score) - 1
Mbtree.calc_score_by_bf = calc_score_by_bf
修正箇所
def calc_score_by_bf(self):
self.nodelist_by_score = self.nodelist[:]
for nodelist in reversed(self.nodelist_by_depth):
for node in nodelist:
if node.mb.status != Marubatsu.PLAYING:
self.calc_score_of_node(node)
else:
score_list = [childnode.score for childnode in node.children]
if node.mb.move_count % 2 == 0:
score = max(score_list)
else:
score = min(score_list)
node.score = score
node.max_score = max([childnode.max_score for childnode in node.children])
node.min_score = min([childnode.min_score for childnode in node.children])
- if -1 < node.score < 1:
- if node.mb.move_count % 2 == 1:
- if node.max_score > 0:
- node.score = 0.5
- else:
- node.score = 0
- else:
- if node.min_score < 0:
- node.score = -0.5
- else:
- node.score = 0
self.nodelist_by_score.append(node)
node.score_index = len(self.nodelist_by_score) - 1
Mbtree.calc_score_by_bf = calc_score_by_bf
Mbtree クラスの recalculate_score の定義
下記は recalculate_score の定義です。引き分けの局面の評価値の再計算 を行う際に、計算を行う 局面の順番 は どのような順番でも構わない ので、幅優先アルゴリズムや、深さ優先アルゴリズムを利用する必要はなく、下記のプログラムの 2 行目 のように、ゲーム木の ノードの一覧が記録 されている nodelist 属性 の中から順番のノードを取り出して評価値の再計算を行うことができます。
-
2 行目:ゲーム木を作成する際に、ゲーム木のノードの一覧は
nodelist属性に代入されるので、それを使って全てのノードに対する繰り返し処理を行う -
3 行目:引き分けの局面であることを
score属性が0であることで判定する。ミニマックス法では引き分けの局面の評価値を0として計算したので、先程のように -1 以上 1 以下という条件で判定する必要はない -
4 ~ 13 行目:先程
calc_score_by_bfから削除した、引き分けの局面の評価値を修正する処理と同じ処理を記述する
1 def recalculate_score(self):
2 for node in self.nodelist:
3 if node.score == 0:
4 if node.mb.move_count % 2 == 1:
5 if node.max_score > 0:
6 node.score = 0.5
7 else:
8 node.score = 0
9 else:
10 if node.min_score < 0:
11 node.score = -0.5
12 else:
13 node.score = 0
14
15 Mbtree.recalculate_score = recalculate_score
行番号のないプログラム
def recalculate_score(self):
for node in self.nodelist:
if node.score == 0:
if node.mb.move_count % 2 == 1:
if node.max_score > 0:
node.score = 0.5
else:
node.score = 0
else:
if node.min_score < 0:
node.score = -0.5
else:
node.score = 0
Mbtree.recalculate_score = recalculate_score
Mbtree クラスの __init__ メソッドの修正
ゲーム木を作成する際 に、引き分けの局面の評価値を再計算するか どうかを recalculate_draw_score という 仮引数で区別 できるように、Mbtree クラスの __init__ メソッドを下記のプログラムのように修正します。
-
3 行目:デフォルト値を
Falseをとする仮引数recalculate_draw_scoreを追加する -
5 行目:
recalculate_draw_scoreを同名の属性に代入する -
6、7 行目:
recalculate_draw_score属性がTrueの場合のみrecalculate_scoreメソッドを呼び出して、引き分けの局面の評価値を再計算する
1 from tree import Node
2
3 def __init__(self, algo="bf", shortest_victory=False, recalculate_draw_score=False, subtree=None):
元と同じなので省略
4 self.shortest_victory = shortest_victory
5 self.recalculate_draw_score = recalculate_draw_score
元と同じなので省略
6 if self.recalculate_draw_score:
7 self.recalculate_score()
8 self.nodelist_by_mb = {}
9 self.bestmoves_by_mb = {}
10 self.calc_bestmoves(self.root)
11
12 Mbtree.__init__ = __init__
行番号のないプログラム
from tree import Node
def __init__(self, algo="bf", shortest_victory=False, recalculate_draw_score=False, subtree=None):
if subtree is not None:
self.subtree = subtree
self.create_subtree()
return
self.algo = algo
self.shortest_victory = shortest_victory
self.recalculate_draw_score = recalculate_draw_score
Node.count = 0
self.root = Node(Marubatsu())
if self.algo == "bf":
self.create_tree_by_bf()
self.calc_score_by_bf()
else:
self.nodelist = [self.root]
self.nodelist_by_depth = [[] for _ in range(10)]
self.nodelist_by_depth[0].append(self.root)
self.nodenum = 0
self.create_tree_by_df(self.root)
self.nodelist_by_score = []
self.calc_score_by_df(self.root)
if self.recalculate_draw_score:
self.recalculate_score()
self.nodelist_by_mb = {}
self.bestmoves_by_mb = {}
self.calc_bestmoves(self.root)
Mbtree.__init__ = __init__
修正箇所
from tree import Node
-def __init__(self, algo="bf", shortest_victory=False, subtree=None):
+def __init__(self, algo="bf", shortest_victory=False, recalculate_draw_score=False, subtree=None):
元と同じなので省略
self.algo = algo
self.shortest_victory = shortest_victory
+ self.recalculate_draw_score = recalculate_draw_score
元と同じなので省略
+ if self.recalculate_draw_score:
+ self.recalculate_score()
self.nodelist_by_mb = {}
self.bestmoves_by_mb = {}
self.calc_bestmoves(self.root)
Mbtree.__init__ = __init__
実行結果は同じなので省略しますが、上記の修正後に下記のプログラムを実行すると、正しい評価値が計算されることが確認できます。なお、局面と最善手・評価値の対応表のデータを保存する ファイルの名前 をこれまで通りの方法でつけると長くなりすぎるので bestmoves_and_score_by_board_sv_rd.dat としました。
mbtree = Mbtree(shortest_victory=True, recalculate_draw_score=True)
data = mbtree.calc_and_save_bestmoves_and_score_by_board("../data/bestmoves_and_score_by_board_sv_rd.dat")
Mbtree_GUI(scoretable_dict={"test": data})
新しい AI に関する処理
上記で新しい評価値を計算したゲーム木を利用した AI の名前を ゲーム木(game tree)を利用した AI、最短の勝利(shortest victory)を目指す AI、引き分けの局面の評価値を再計算(recalculate draw score)AI であることからそれらの頭文字を取って ai_gtsvrd と表記することにし、この AI に関するいくつかの処理を行うことにします。
ai2s との対戦
下記のプログラムで ai_gtsrvd とランダムな着手を行う ai2s で対戦 を行うことで、その 性能を評価 することにします。
from ai import ai_match, ai2, ai_gt7
ai_match(ai=[ai_gt7, ai2], params=[{"bestmoves_and_score_by_board": data}, {}])
実行結果(実行結果はランダムなので下記と異なる場合があります)
ai_gt7 VS ai2
100%|██████████| 10000/10000 [00:03<00:00, 2800.99it/s]
count win lose draw
o 9714 0 286
x 8110 0 1890
total 17824 0 2176
ratio win lose draw
o 97.1% 0.0% 2.9%
x 81.1% 0.0% 18.9%
total 89.1% 0.0% 10.9%
下記は、ルールベースの AI の中で最後に作成した ai14s、ゲーム木を利用した最初の AI である ai_gt1、ai_gtsvrd のそれぞれが ai2s と対戦した結果をまとめた表です。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 |
|---|---|---|---|---|---|---|---|---|---|
ai14s |
99.0 | 0.0 | 1.0 | 88.8 | 0.0 | 11.2 | 93.9 | 0.0 | 6.1 |
ai_gt1 |
96.9 | 0.0 | 3.1 | 78.0 | 0.0 | 22.1 | 87.4 | 0.0 | 12.6 |
ai_gtsvrd |
97.1 | 0.0 | 2.9 | 81.1 | 0.0 | 18.9 | 89.1 | 0.0 | 10.9 |
上記の表から、引き分けの評価値を再計算しない ai_gt1 と比較して、ai_gtsvrd は特に × を担当した場合の勝率が向上していることが確認できます。
ai14s よりも勝率が劣る理由
残念ながら ai14s と比較すると ai_gtsvrd の勝率は劣ります が、その理由はランダムな着手を行う AI と対戦した際に、引き分けの局面の最善手の中で、相手が最善手を着手しなかった場合に勝利できる合法手 にも 優劣が存在する からです。
わかりづらいと思いますので具体例を挙げて説明します。下図の赤枠の 〇 の手番の局面の 合法手のうち (1, 0)、(2, 0)、(1, 2)、(2, 2) は評価値が 0.5 と表示されているので、その 子孫ノードに 〇 が勝利する局面が存在 します。

下図は (1, 0) に着手 した場合の局面を中心とする 部分木 です。図からこの局面の 4 つある合法手のうち 3 つ は 最善手ではない ため、相手がそれらを選択すると常に最善手を選択する 強解決の AI である ai_svgtrd は 100 % 勝利 することができます。従って、ai2s がこの局面で ランダムに着手を選択 すると 3/4 = 75 % の確率 で ai_gtsvrd は勝利 することができます。ai2s が (1, 2) に着手を行った場合の ai_gtsvrd が勝利する確率は、その子孫ノードを見て確率を計算する必要がありますが、上図の局面で ai_gtsvrd が (1, 0) に着手 を行った場合に 勝利する確率 は 少なくとも 75 % 以上 であることは間違いありません。
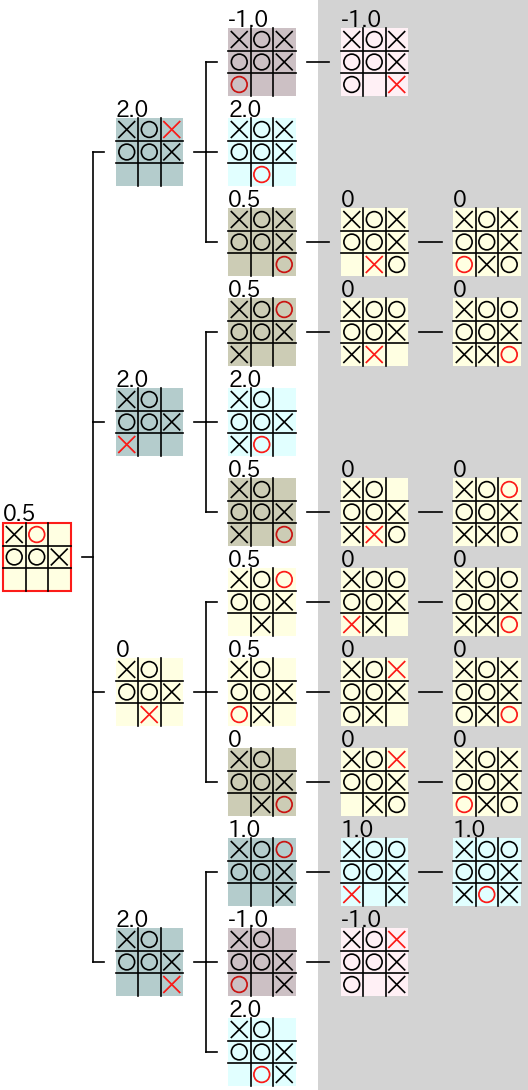
このように、常に最善手を選択する 強解決の AI が ランダムな着手を行う ai2s と対戦 する場合は、ai2s の手番 の局面の合法手の中の、最善手でない合法手 の 割合が高い程勝率が高くなる という傾向があります3。
一方、下図は (2, 2) に着手 した場合の局面を中心とする 部分木 です。図からこの局面は 全ての合法手 が 引き分けの局面になる最善手 なので、ai2s がどの着手を行っても、次の 〇 の手番の局面で 〇 が勝利が確定しない ことがわかります。正確な 〇 の勝利の確率は下図の子孫ノードを調べなければ確認できませんが、先程の局面で ai_gtsvrd が (1, 0) に着手 を行った場合に 勝利する確率 よりも 低い可能性が非常に高い でしょう。

このことから、相手がランダムな着手を行う AI の場合は、引き分けの局面の最善手の中で 相手が最善手を着手しなかった場合に勝利できる合法手 に実際に 優劣が存在する ことが確認できました。ai14s のほうが ai_gtsvrd よりも ai2s に対する勝率が高いのは、ai14s が 最善手の割合が少ない局面になる合法手 を ai_gtsvrd よりも選択する からです。
なお、相手が 人間の場合 は上記の (1, 0) のほうが (2, 2) よりも 優れているとは限りません。それは、人間が 合法手の中から 着手を選択する際 に、一般的に ランダムに選択することはない からです。そのため、合法手の中で 人間が選択しやすい ものと、そうでないものが存在 します。人間の手番の合法手の中で、人間が最善手を選択しやすい 簡単な局面の場合 は 最善手の割合がどれだけ少なくても AI が有利になることはありません。そのため、引き分けの局面で 人間に勝ちやすい AI を作成する ためには、最善手の中で 人間が間違えやすいような難しい局面になる ような着手を行うことが重要になります。
ただし、人間にとって難しい局面 がどのような局面であるかを 判断する方法は簡単ではありません。そのためには、ミニマックス法や、最善手の割合以外の 別の評価値を計算する方法を考える 必要があり、どのようなゲームでもそのような判断を行うための 統一的な方法はまだ見つかっていない と思います。
将棋などでは、不利な局面 で最善手を着手するのではなく、相手が間違えやすい難しい局面になる ような あえて最善手ではない着手 を選択することで、逆転を狙う ということが良く行われます。そのような着手は 相手が最善手を着手した場合はさらに不利になる ので相手が AI の場合は基本的には通用しませんが、人間が相手の場合は逆転につながることが実際にあります。
余談ですが、将棋の AI が現在と比べてまだ弱かった頃に行われた AI とプロ棋士の対戦で、AI の弱点をついた最善手ではない着手を選択することで AI に勝利するという試合が実際に行われたことがあります。
なお、現在の将棋などの AI では、原則として 最善手を着手することを目指 すように作られているので、そのような着手を行うことはありません。
逆に 初心者 のように、相手が弱い ことがわかっている場合は、あえて最善手を選択しないことで、手加減をすることが重要になる ことがあります。例えば、初心者に圧勝してしまうと、そのゲームが嫌になってしまう可能性が高いからです。本記事では紹介しませんが、相手のレベルに合わせて手加減をうまく行う ような AI を作成するためには、ミニマックス法以外の 別の工夫が必要 になります。
強解決の AI であるかどうかの確認
念のため、ai_gtsvrd が 強解決の AI であるか を下記のプログラムで確認することにします。実行結果から強解決の AI であることが確認できました。
from util import Check_solved
Check_solved.is_strongly_solved(ai_gt7, {"bestmoves_and_score_by_board": data})
実行結果
100%|██████████| 431/431 [00:00<00:00, 3905.72it/s]
431/431 100.00%
(True, [])
ゲーム木のデータの保存
作成したゲーム木のデータが正しいことが確認できたので、下記のプログラムでゲーム木のデータを bftree_svrd.dat というファイルに保存 することにします。
mbtree.save("../data/bftree_svrd")
実行結果
save completed.
gui_play への組み込み
gui_play を下記のプログラムのように修正して、ai_gtsvrd を Dropdown で選択できる ようにします。
-
5、6 行目:ファイルからデータを読み込んで Dropdown に
ai_gtsvrdの項目を追加する
1 import ai as ai_module
2 from util import load_bestmoves
3
4 def gui_play(ai=None, params=None, ai_dict=None, seed=None):
元と同じなので省略
5 bestmoves_and_score_by_board_svrd = load_bestmoves("../data/bestmoves_and_score_by_board_sv_rd.dat")
6 ai_dict["ai_gtsvrd"] = (ai_gt7, {"bestmoves_and_score_by_board": bestmoves_and_score_by_board_svrd})
元と同じなので省略
行番号のないプログラム
import ai as ai_module
from util import load_bestmoves
def gui_play(ai=None, params=None, ai_dict=None, seed=None):
# ai が None の場合は、人間どうしの対戦を行う
if ai is None:
ai = [None, None]
if params is None:
params = [{}, {}]
# ai_dict が None の場合は、ai1s ~ ai14s の Dropdown を作成するためのデータを計算する
if ai_dict is None:
ai_dict = { "人間": ( None, {} ) }
for i in range(1, 15):
ai_name = f"ai{i}s"
ai_dict[ai_name] = (getattr(ai_module, ai_name), {})
bestmoves_and_score_by_board = load_bestmoves("../data/bestmoves_and_score_by_board.dat")
ai_dict["ai_gt7"] = (ai_gt7, {"bestmoves_and_score_by_board": bestmoves_and_score_by_board})
bestmoves_and_score_by_board_sv = load_bestmoves("../data/bestmoves_and_score_by_board_shortest_victory.dat")
ai_dict["ai_gtsv"] = (ai_gt7, {"bestmoves_and_score_by_board": bestmoves_and_score_by_board_sv})
bestmoves_and_score_by_board_svrd = load_bestmoves("../data/bestmoves_and_score_by_board_sv_rd.dat")
ai_dict["ai_gtsvrd"] = (ai_gt7, {"bestmoves_and_score_by_board": bestmoves_and_score_by_board_svrd})
mb = Marubatsu()
mb.play(ai=ai, params=params, ai_dict=ai_dict, seed=seed, gui=True)
修正箇所
import ai as ai_module
from util import load_bestmoves
def gui_play(ai=None, params=None, ai_dict=None, seed=None):
元と同じなので省略
+ bestmoves_and_score_by_board_svrd = load_bestmoves("../data/bestmoves_and_score_by_board_sv_rd.dat")
+ ai_dict["ai_gtsvrd"] = (ai_gt7, {"bestmoves_and_score_by_board": bestmoves_and_score_by_board_svrd})
元と同じなので省略
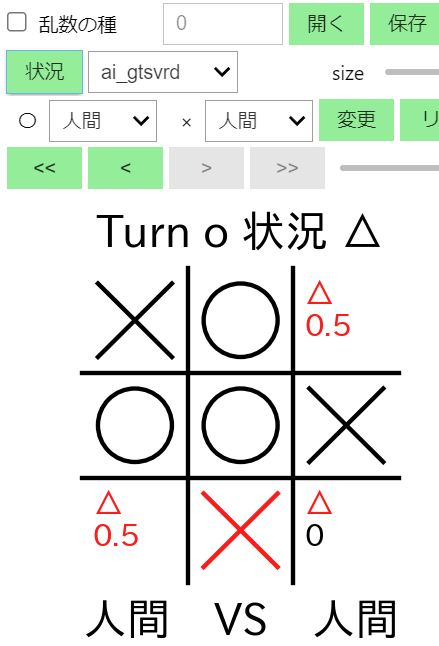
上記の修正後に下記のプログラムを実行し、先程の局面になるように着手を行った後で「状況」ボタンをクリックし、の右の Dropdown に ai_gtsvrd を選択 すると、実行結果の左下図のように相手が間違えた場合に 勝利できる可能性がある (0, 2) と (2, 0) の評価値は 0.5、絶対に勝利できない (2, 2) の評価値は 0 が計算されることが確認できます。また、Dropdown に ai_gtsv を選択すると右下図のように すべての合法手の評価値が 0 で 赤字で表示される ため、(2, 2) に着手してしまう可能性がある 事が確認できます。
gui_play()
実行結果
Mbtree_GUI クラスの __init__ メソッド の修正
最後に。Mbtree_GUI クラスの __init__ メソッドに下記のプログラムの 5 行目を追加 することで、ゲーム木を表示する GUI の Dropdown に Recalculate Draw というラベルで ai_gtsvrd のデータを選択できる ように修正します。なお、前回の記事で ai_gt7 を作成したので、それに合わせて 3 行目 の Dropdown の項目の ラベルを ai_gt6 から ai_gt7 に修正 しました。
1 def __init__(self, scoretable_dict=None, show_score=True, size=0.15):
元と同じなので省略
2 scoretable_dict = {
3 "Standard (ai_gt7)": load_bestmoves("../data/bestmoves_and_score_by_board.dat"),
4 "Shortest victory (ai_gtsv)": load_bestmoves("../data/bestmoves_and_score_by_board_shortest_victory.dat"),
5 "Recalculate draw (ai_gtsvrd)": load_bestmoves("../data/bestmoves_and_score_by_board_sv_rd.dat"),
6 }
元と同じなので省略
7
8 Mbtree_GUI.__init__ = __init__
行番号のないプログラム
def __init__(self, scoretable_dict=None, show_score=True, size=0.15):
if scoretable_dict is None:
from util import load_bestmoves
scoretable_dict = {
"Standard (ai_gt7)": load_bestmoves("../data/bestmoves_and_score_by_board.dat"),
"Shortest victory (ai_gtsv)": load_bestmoves("../data/bestmoves_and_score_by_board_shortest_victory.dat"),
"Recalculate draw (ai_gtsvrd)": load_bestmoves("../data/bestmoves_and_score_by_board_sv_rd.dat"),
}
self.scoretable_dict = scoretable_dict
self.show_score = show_score
self.size = size
self.width = 50
self.height = 65
self.selectednode = Node(Marubatsu())
super(Mbtree_GUI, self).__init__()
Mbtree_GUI.__init__ = __init__
修正箇所
def __init__(self, scoretable_dict=None, show_score=True, size=0.15):
元と同じなので省略
scoretable_dict = {
- "Standard (ai_gt6)": load_bestmoves("../data/bestmoves_and_score_by_board.dat"),
+ "Standard (ai_gt7)": load_bestmoves("../data/bestmoves_and_score_by_board.dat"),
"Shortest victory (ai_gtsv)": load_bestmoves("../data/bestmoves_and_score_by_board_shortest_victory.dat"),
+ "Recalculate draw (ai_gtsvrd)": load_bestmoves("../data/bestmoves_and_score_by_board_sv_rd.dat"),
}
元と同じなので省略
Mbtree_GUI.__init__ = __init__
上記の修正後に下記のプログラムを実行し、Dropdown に Recaluculate draw を選択してから先程の局面を選択すると、下図のように ai_gtsvrd のデータで部分木のノードの上に 再計算された評価値が表示 されるようになったことが確認できます。
gui_play()
実行結果

必敗の局面での合法手の優劣
必敗の局面 では、すべての合法手が最善手になりますが、その場合の合法手に対しても 何らかの方法で優劣をつける ことが可能です。
例えば、〇 が着手を行った 〇 の必敗の局面 に対して下記のような評価値を計算することで、〇 の手番の必敗の局面 に対して「勝利する可能性がある合法手 > 引き分けになる可能性がある合法手 > 絶対に敗北する合法手」という優劣をつけることができます。
- 〇 の必敗の局面なので、負の評価値を計算 する
- 子孫ノード に 〇 が勝利するノードが存在 する場合は -1 の評価値を計算する
- そうではなく、子孫ノードに 引き分けのノードが存在 する場合は -2 の評価値を計算する
- そうではなく、敗北するノードしか存在しない 場合は -2 未満の評価値 を計算する
× の手番の × の必敗の局面に対しても同様です。
なお、本記事ではそのような評価値を計算する処理は実装しません。その理由はゲーム開始時の局面が引き分けの局面である 〇×ゲーム では、強解決の AI が対戦を行った場合に、その AI が 必敗になる局面が生じることはない からです。そのため、そのような AI を作成して ai2s と対戦 しても、勝率が良くなることはありません。
なお、最善手を着手しない可能性がある AI や 人間 が 着手を行った局面 に対して、評価値を計算したい場合 は、そのような AI を作成する 意味が生じます ので、興味と余裕がある方は実装してみて下さい。
今回の記事のまとめ
今回の記事では、前回の記事で実装したプログラムのバグの検証と修正を行いました。また、ミニマックス法による評価値の計算 と、引き分けの局面の評価値の再計算 の処理を 分離して実装する 方法を紹介しました。
最後に、作成した AI を gui_play などで選択できるようにしました。
本記事で入力したプログラム
| リンク | 説明 |
|---|---|
| marubatsu.ipynb | 本記事で入力して実行した JupyterLab のファイル |
| tree.py | 本記事で更新した tree_new.py |
| util.py | 本記事で更新した util_new.py |
次回の記事