Pythonで〇×ゲームのAIを一から作成する　その166　スカウト法の実装と効率

Posted at 2025-04-24

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。　

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
test.py	テストに関する関数
util.py	ユーティリティ関数の定義。現在は `gui_play` のみ定義されている
tree.py	ゲーム木に関する Node、Mbtree クラスの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

スカウト法の実装と効率の確認

前回の記事では、αβ 法を改良した スカウト法 を紹介しました。スカウト法は move ordering を前提とする、以下のような考え方の手法です。

精度の高い move ordering によって 最善手の子ノードが先頭に移動 したと 仮定する
先頭の子ノードの処理は αβ 法同じ処理を行い、2 番目以降の子ノードの処理 を以下のように行う
仮定が正しい場合 は null window search を行う ことで、αβ 法以上 の枝狩りの 効率を得る ことができる
仮定が正しくない場合 は αβ 法で計算処理をやり直し、計算された評価値が最大の評価値であると 仮定し直して処理を続ける
仮定が正しくない場合 は null window search を行なった分だけ αβ 法よりも効率が悪くなる が、move ordering の精度が充分高ければ 総合的に見て αβ 法以上の効率を得る ことが 期待できる

今回の記事ではスカウト法を実装し、その効率を確認します。

null window search に関する補足

以前の記事では評価値が 3 種類の場合の null window serach の利用例を紹介しましたが、null window search をそのような目的で利用することはほとんどないと思います。null window search は 一般的に スカウト法で利用した場合のように、ミニマックス値が特定の値以下（または以上）であるかどうかを 効率よく判定するために利用 されます。

今回の記事で利用する記号

今回の記事では以下の記号を使って説明を行います。

以前の記事と同様に、ノードの評価値を計算する際の α 値と β 値の初期値 を $\boldsymbol{α}$、$\boldsymbol{β}$ と表記する。また、次の子ノードの評価値を計算する時点での α 値と β 値 は、α 値、β 値 と表記して区別する
αβ 法でノードの評価値を計算する際に下記の記号を用いる
- α 値と β 値の範囲を表す ウィンドウ を (α 値, β 値) のように () の記号で表記 する
- $\boldsymbol{i}$ 番目の子ノードの評価値 を $\boldsymbol{s_i}$ と表記する
- それまでに計算されたノードの評価値 を $\boldsymbol{s}$ と表記する。$s$ は max ノードではそれまでに計算された子ノードの評価値の最大値、min ノードでは最小値である
$a$ と $b$ の最大値を $max(a, b)$、最小値を $min(a, b)$ と表記する

スカウト法のアルゴリズム

下記は前回の記事で説明した スカウト法のアルゴリズムの再掲 です。ただし、前回の記事で説明したように、手順 3-1 の処理は null window search なので、前回の記事で「αβ 法」と記述していた部分を null window search に改めました。

move ordering を行う
先頭の子ノードの評価値の計算処理 を αβ 法と同じ 方法で計算する
2 番目以降の子ノード の評価値の計算処理を以下の手順で行う。以下は $i$（$i ≧ 2$）番目の子ノードの評価値 $s_i$ を計算する場合の処理の説明である
- max ノード の場合は以下の手順で計算を行う
  1. ウィンドウを (α 値, α 値 + 1) とした null window search で $s_i$ を計算し、$s$ を更新する
  2. $s$ の値に応じて以下の処理を行う
    1. β 値 ≦ $\boldsymbol{s}$ の場合は $s$ をこのノードの評価値として処理を終了するという、β 狩り の処理を行う
    2. α 値 < $\boldsymbol{s}$ < β 値 の場合は ウィンドウを (α 値, β 値) とした αβ 法と同じ方法 で 計算しなおす。$s$ や α 値の更新、β 狩りの処理も αβ 法と同じ処理を行う
    3. $\boldsymbol{s}$ ≦ α 値 の場合は何もしない
- min ノード の場合は以下の手順で計算を行う
  1. ウィンドウを (β 値 - 1, β 値) とした null window search で $s_i$ を計算し、$s$ を更新する
  2. $s$ の値に応じて以下の処理を行う
    1. $\boldsymbol{s}$ ≦ α 値 の場合は $s$ をこのノードの評価値として処理を終了するという、β 狩り の処理を行う
    2. α 値 < $\boldsymbol{s}$ < β 値 の場合は ウィンドウを (α 値, β 値) とした αβ 法と同じ方法 で 計算しなおす。$s$ や β 値の更新、α 狩りの処理も αβ 法と同じ処理を行う
    3. β 値 ≦ $\boldsymbol{s}$ の場合は何もしない

ネガスカウト法

スカウト法は一般的には 評価値の符号を反転させる ことで max ノードと min ノードの処理をまとめる という ネガスカウト法 で実装されることが多いようです。また、プログラムが少しわかりづらくなるので本記事では紹介しませんでしたが、最初の子ノードの処理と、2 番目以降の子ノードの処理をまとめるという実装方法もあります。

具体的なプログラムの例については下記のネガスカウト法の Wikipedia と Chess Programmin wiki を参照して下さい。

`ai_scout` の定義

上記のアルゴリズムのスカウト法で着手を選択する ai_scout という関数を定義する事にします。スカウト法 は αβ 法に上記の手順 3 を加えたもの なので、αβ 法で着手を選択する ai_abs_all を修正して定義 する事にします。従って、ai_scout と ai_abs_all の 仮引数や返り値は同じ です。

下記は ai_scout を定義するプログラムです。下記では表示を省略していますが、11 行目の前で ai_abs_all と同じ方法で move ordering の処理を行う ことで、move ordering 利用する AI の関数が同じであれば、同じノードで同じ move ordering が行われます。

6 行目：関数名を ai_scout に修正する
12 ~ 16 行目：最初の子ノードの評価値を αβ 法と同じウィンドウで計算し、$s$(score) と α 値(alpha) を計算する
17 行目：β 狩りが行なわれる場合は残りの子ノードの処理が省略されるので、β 狩りが行なわれない場合のみ残りの子ノードの処理を行うように修正する
18 ~ 28 行目：list のスライス表記を使って 2 番目以降の子ノードの繰り返し処理を行うように修正する
19 ~ 21 行目：ウィンドウを (α 値, α 値 + 1) とした null window search で子ノードの評価値の計算を行ない、$s$ を更新する（手順 3-1）
22、23 行目：β 値 ≦ $s$ の場合は β 狩りを行うので繰り返し処理を終了する（手順 3-2-1）
24 ~ 28 行目：α 値 < $s$ < β 値¹ の場合は、αβ 法と同じ (α 値, β 値) のウィンドウで子ノードの評価値の計算をやり直す。26、27 行目で β 狩り、28 行目で β 値の更新処理を行う（手順 3-2-2）
29 ~ 46 行目：min ノードで上記と同様の処理を行うように修正する

 1  from ai import ai_by_score, dprint
 2  from marubatsu import Marubatsu
 3  from copy import deepcopy
 4
 5  @ai_by_score
 6  def ai_scout(mb, debug=False, shortest_victory=False,
 7               init_ab=False, use_tt=False, ai_for_mo=None,
 8               params={}, sort_allnodes=False, calc_count=False):        
 9      count = 0
10      def ab_search(mborig, tt, alpha=float("-inf"), beta=float("inf")):
元と同じなので省略
11          if mborig.turn == Marubatsu.CIRCLE:
12              x, y = legal_moves[0]
13              mb = deepcopy(mborig)
14              mb.move(x, y)
15              score = ab_search(mb, tt, alpha, beta)
16              alpha = max(alpha, score)
17              if score < beta:
18                  for x, y in legal_moves[1:]:
19                      mb = deepcopy(mborig)
20                      mb.move(x, y)
21                      score = max(score, ab_search(mb, tt, alpha, alpha + 1))
22                      if score >= beta:
23                          break
24                      elif score > alpha:
25                          score = max(score, ab_search(mb, tt, alpha, beta))
26                          if score >= beta:
27                              break
28                          alpha = max(alpha, score)
29          else:
30              x, y = legal_moves[0]
31              mb = deepcopy(mborig)
32              mb.move(x, y)
33              score = ab_search(mb, tt, alpha, beta)
34              beta = min(beta, score)
35              if score > alpha:
36                  for x, y in legal_moves[1:]:
37                      mb = deepcopy(mborig)
38                      mb.move(x, y)
39                      score = min(score, ab_search(mb, tt, beta - 1, beta))
40                      if score <= alpha:
41                          break
42                      elif score < beta:
43                          score = min(score, ab_search(mb, tt, alpha, beta))
44                          if score <= alpha:
45                              break
46                          beta = min(beta, score)
元と同じなので省略

行番号のないプログラム

from ai import ai_by_score, dprint
from marubatsu import Marubatsu
from copy import deepcopy

@ai_by_score
def ai_scout(mb, debug=False, shortest_victory=False,
             init_ab=False, use_tt=False, ai_for_mo=None,
             params={}, sort_allnodes=False, calc_count=False):        
    count = 0
    def ab_search(mborig, tt, alpha=float("-inf"), beta=float("inf")):
        nonlocal count
        count += 1
        if mborig.status == Marubatsu.CIRCLE:
            return (11 - mborig.move_count) / 2 if shortest_victory else 1
        elif mborig.status == Marubatsu.CROSS:
            return (mborig.move_count - 10) / 2 if shortest_victory else -1
        elif mborig.status == Marubatsu.DRAW:
            return 0
        
        if use_tt:
            boardtxt = mborig.board_to_str()
            if boardtxt in tt:
                lower_bound, upper_bound = tt[boardtxt]
                if lower_bound == upper_bound:
                    return lower_bound
                elif upper_bound <= alpha:
                    return upper_bound
                elif beta <= lower_bound:
                    return lower_bound
                else:
                    alpha = max(alpha, lower_bound)
                    beta = min(beta, upper_bound)
            else:
                lower_bound = min_score
                upper_bound = max_score
        
        alphaorig = alpha
        betaorig = beta

        legal_moves = mborig.calc_legal_moves()
        if ai_for_mo is not None:
            if sort_allnodes:
                score_by_move = ai_for_mo(mborig, analyze=True, **params)["score_by_move"]
                score_by_move_list = sorted(score_by_move.items(), key=lambda x:x[1], reverse=True)
                legal_moves = [x[0] for x in score_by_move_list]
            else:
                legal_moves = mborig.calc_legal_moves()
                bestmove = ai_for_mo(mborig, rand=False, **params)
                index = legal_moves.index(bestmove)
                legal_moves[0], legal_moves[index] = legal_moves[index], legal_moves[0]

        if mborig.turn == Marubatsu.CIRCLE:
            x, y = legal_moves[0]
            mb = deepcopy(mborig)
            mb.move(x, y)
            score = ab_search(mb, tt, alpha, beta)
            alpha = max(alpha, score)
            if score < beta:
                for x, y in legal_moves[1:]:
                    mb = deepcopy(mborig)
                    mb.move(x, y)
                    score = max(score, ab_search(mb, tt, alpha, alpha + 1))
                    if score >= beta:
                        break
                    elif score > alpha:
                        score = max(score, ab_search(mb, tt, alpha, beta))
                        if score >= beta:
                            break
                        alpha = max(alpha, score)
        else:
            x, y = legal_moves[0]
            mb = deepcopy(mborig)
            mb.move(x, y)
            score = ab_search(mb, tt, alpha, beta)
            beta = min(beta, score)
            if score > alpha:
                for x, y in legal_moves[1:]:
                    mb = deepcopy(mborig)
                    mb.move(x, y)
                    score = min(score, ab_search(mb, tt, beta - 1, beta))
                    if score <= alpha:
                        break
                    elif score < beta:
                        score = min(score, ab_search(mb, tt, alpha, beta))
                        if score <= alpha:
                            break
                        beta = min(beta, score)   
            
        if use_tt:
            from util import calc_same_boardtexts

            boardtxtlist = calc_same_boardtexts(mborig)
            if score <= alphaorig:
                upper_bound = score
            elif score < betaorig:
                lower_bound = score
                upper_bound = score
            else:
                lower_bound = score
            for boardtxt in boardtxtlist:
                tt[boardtxt] = (lower_bound, upper_bound)
        return score
                
    min_score = -2 if shortest_victory else -1
    max_score = 3 if shortest_victory else 1
    alpha = min_score if init_ab else float("-inf")
    beta = max_score if init_ab else float("inf")

    score = ab_search(mb, {}, alpha=alpha, beta=beta)
    dprint(debug, "count =", count)
    if calc_count:
        return count
    if mb.turn == Marubatsu.CIRCLE:
        score *= -1
    return score

修正箇所

from ai import ai_by_score, dprint
from marubatsu import Marubatsu
from copy import deepcopy

@ai_by_score
-def ai_abs_all(mb, debug=False, shortest_victory=False,
+def ai_scout(mb, debug=False, shortest_victory=False,
             init_ab=False, use_tt=False, ai_for_mo=None,
             params={}, sort_allnodes=False, calc_count=False):        
    count = 0
    def ab_search(mborig, tt, alpha=float("-inf"), beta=float("inf")):
元と同じなので省略
        if mborig.turn == Marubatsu.CIRCLE:
-           score = float("-inf")
-           for x, y in legal_moves:
-               mb = deepcopy(mborig)
-               mb.move(x, y)
-               score = max(score, ab_search(mb, tt, alpha, beta))
-               if score >= beta:
-                   break
-               alpha = max(alpha, score)
+           x, y = legal_moves[0]
+           mb = deepcopy(mborig)
+           mb.move(x, y)
+           score = ab_search(mb, tt, alpha, beta)
+           alpha = max(alpha, score)
+           if score < beta:
+               for x, y in legal_moves[1:]:
+                   mb = deepcopy(mborig)
+                   mb.move(x, y)
+                   score = max(score, ab_search(mb, tt, alpha, alpha + 1))
+                   if score >= beta:
+                       break
+                   elif score > alpha:
+                       score = max(score, ab_search(mb, tt, alpha, beta))
+                       if score >= beta:
+                           break
+                       alpha = max(alpha, score)
        else:
-           score = float("inf")
-           for x, y in legal_moves:
-               mb = deepcopy(mborig)
-               mb.move(x, y)
-               score = min(score, ab_search(mb, tt, alpha, beta))
-               if score <= alpha:
-                   break
-               beta = min(beta, score) 
+           x, y = legal_moves[0]
+           mb = deepcopy(mborig)
+           mb.move(x, y)
+           score = ab_search(mb, tt, alpha, beta)
+           beta = min(beta, score)
+           if score > alpha:
+               for x, y in legal_moves[1:]:
+                   mb = deepcopy(mborig)
+                   mb.move(x, y)
+                   score = min(score, ab_search(mb, tt, beta - 1, beta))
+                   if score <= alpha:
+                       break
+                   elif score < beta:
+                       score = min(score, ab_search(mb, tt, alpha, beta))
+                       if score <= alpha:
+                           break
+                       beta = min(beta, score)   
元と同じなので省略

ai_abs_all では、max ノードでは score にそれまでに計算された子ノードの評価値の最大値を計算する必要があるため、score を負の無限大で初期化し、子ノードの繰り返し処理の中で score = max(score, ab_search(mb, tt, alpha, beta) という計算を行なっていました。

一方、ai_scout では最初の子ノードの処理を繰り返し処理の前に行うため、最初の子ノードの評価値が計算された時点ではその評価値が最大値となります。そのため score を負の無限大で初期化するという処理を削除し、15 行目では最初の子ノードの評価値を score にそのまま代入するという処理を行っています。

上記の定義後に、以前の記事で ai_abs_all が 強解決であるかどうか を確認したのと同様の方法で ai_scout が強解決の AI であるかどうかを確認すると、実行結果から いずれの設定の場合でも強解決の AI であることが確認できます。

なお、スカウト法は move ordering を前提とするアルゴリズムですが、move ordering を行わない場合でも効率が悪いだけで強解決であることには変わらない ので、下記では move ordering を行わない場合も確認しています。また、先頭のみの move ordering と全ノードの move ordering の両方を確認するように修正しました。

from util import Check_solved
from ai import ai2s, ai14s

for ai_for_mo in [None, ai2s, ai14s]:
    for shortest_victory in [False, True]:
        for use_tt in [False, True]:
            for init_ab in [False, True]:
                for sort_allnodes in [False, True]:
                    print(f"ai_for_mo: {ai_for_mo}, sv: {shortest_victory}, use_tt: {use_tt}, init_ab: {init_ab} sort: {sort_allnodes}")
                    params = {
                        "ai_for_mo": ai_for_mo,
                        "shortest_victory": shortest_victory,
                        "init_ab": init_ab,
                        "use_tt": use_tt,
                        "sort_allnodes": sort_allnodes,
                    }
                    Check_solved.is_strongly_solved(ai_scout, params=params)

修正箇所

from util import Check_solved
from ai import ai2s, ai14s

for ai_for_mo in [None, ai2s, ai14s]:
    for shortest_victory in [False, True]:
        for use_tt in [False, True]:
            for init_ab in [False, True]:
+               for sort_allnodes in [False, True]:
-                   print(f"ai_for_mo: {ai_for_mo}, sv: {shortest_victory}, use_tt: {use_tt}, init_ab: {init_ab}")
+                   print(f"ai_for_mo: {ai_for_mo}, sv: {shortest_victory}, use_tt: {use_tt}, init_ab: {init_ab} sort: {sort_allnodes}")
                    params = {
                        "ai_for_mo": ai_for_mo,
                        "shortest_victory": shortest_victory,
                        "init_ab": init_ab,
                        "use_tt": use_tt,
-                       "sort_allnodes": True,
+                       "sort_allnodes": sort_allnodes,
                    }
                    Check_solved.is_strongly_solved(ai_scout, params=params)
-               Check_solved.is_strongly_solved(ai_abs_all, params=params)
+               Check_solved.is_strongly_solved(ai_scout, params=params)

実行結果

ai_for_mo: None, sv: False, use_tt: False, init_ab: False sort: False
100%|██████████| 431/431 [00:04<00:00, 100.60it/s]
431/431 100.00%
ai_for_mo: None, sv: False, use_tt: False, init_ab: False sort: True
100%|██████████| 431/431 [00:04<00:00, 101.34it/s]
略

スカウト法の効率の確認

スカウト法の効率を確認 するために、以前の記事で行った下記の方法で、αβ 法とスカウト法の枝狩りの効率を比較 することにします。ただし、スカウト法は move ordering を行うことが前提のアルゴリズムなので、move ordering を行わない場合の比較は行ないません。なお、move ordering の処理では前回の記事で修正した ai_abs_all と同じ処理を ai_scout で行うので、仮引数 ai_for_mo に代入された move ordering を行う AI の関数が同じであれば、ai_abs_all と ai_scout は同一の局面に対して同じ move ordering を行ないます。

同一局面を除いた〇×ゲームのすべての局面に対して、同一の設定で αβ 法とスカウト法で計算を行う
それぞれの場合で、計算されたノードの数の合計を比較することで処理の効率を比較する

下記はその比較を行うプログラムです。以前の記事のプログラムとの違いは以下の通りです。なお、結果の数値が多くなりすぎるとわかりづらくなるので、move ordering に関しては 先頭のみの move ordering だけで比較 しました。

以前の記事では全ノードの move ordering を行うかどうかで比較を行ってたが、下記のプログラムでは ai_abs_all と ai_scout の比較を行っている
結果の表示をわかりやすくなるように少しだけ変えた

from util import load_mblist
from ai import ai10s

mblist = load_mblist("../data/mblist_by_board_min.dat")
for ai_for_mo in [ai10s, ai14s]:
    for shortest_victory in [False, True]:
        for use_tt in [False, True]:
            for init_ab in [False, True]:
                print(f"ai_for_mo: {ai_for_mo}, sv: {shortest_victory}, init_ab: {init_ab}, use_tt: {use_tt}")
                count = 0
                count2 = 0
                for mb in mblist:
                    count += ai_abs_all(mb, ai_for_mo=ai_for_mo,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
                                        sort_allnodes=False, calc_score=True, calc_count=True)
                    count2 += ai_scout(mb, ai_for_mo=ai_for_mo,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
                                        sort_allnodes=False, calc_score=True, calc_count=True)
                print("abs count=", count)
                print("scout count=", count2)

修正箇所

from util import load_mblist
from ai import ai10s

mblist = load_mblist("../data/mblist_by_board_min.dat")
for ai_for_mo in [ai10s, ai14s]:
    for shortest_victory in [False, True]:
        for use_tt in [False, True]:
            for init_ab in [False, True]:
                print(f"ai_for_mo: {ai_for_mo}, sv: {shortest_victory}, init_ab: {init_ab}, use_tt: {use_tt}")
                count = 0
                count2 = 0
                for mb in mblist:
                    count += ai_abs_all(mb, ai_for_mo=ai_for_mo,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
                                        sort_allnodes=False, calc_score=True, calc_count=True)
-                   count2 += ai_abs_all(mb, ai_for_mo=ai_for_mo,
+                   count2 += ai_scout(mb, ai_for_mo=ai_for_mo,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
-                                       sort_allnodes=True, calc_score=True, calc_count=True)
+                                       sort_allnodes=False, calc_score=True, calc_count=True)
-               print("count=", count)
-               print("count2=", count2)
+               print("abs count=", count)
+               print("scout count=", count2)

実行結果

ai_for_mo: <function ai10s at 0x0000016BFAD09EE0>, sv: False, init_ab: False, use_tt: False
abs count= 13866
scout count= 14726
ai_for_mo: <function ai10s at 0x0000016BFAD09EE0>, sv: False, init_ab: True, use_tt: False
abs count= 8769
scout count= 9400
ai_for_mo: <function ai10s at 0x0000016BFAD09EE0>, sv: False, init_ab: False, use_tt: True
abs count= 10384
scout count= 10392
略

下記は実行結果をまとめた表です。一番上の行の ab は init_ab、tt は use_tt の値で〇は True、× は False を表します。各セルの 上段が ai_abs_all、下段が ai_scout の場合です。

最短の勝利を目指さない（shortest_victory=False）場合

	ab × tt ×	ab 〇 tt x	ab × tt 〇	ab 〇 tt 〇
`ai10s`	13866 14726	8769 9400	10384 10392	6651 6837
`ai14s`	10679 10839	6127 6194	8792 8761	5016 5028

最短の勝利を目指す（shortest_victory=True）場合

	ab × tt ×	ab 〇 tt x	ab × tt 〇	ab 〇 tt 〇
`ai10s`	15135 15645	13145 14052	11091 11135	9743 9918
`ai14s`	10691 10869	9263 9441	8808 8850	7561 7603

上記の結果から、ai10s を利用して move ordering を行う場合は、下段のスカウト法のほうが 上段の αβ 法よりもほとんどの場合で評価値を計算したノードの数が多く、効率が悪い ことがわかります。これは、ai10s による move ordering は 精度が充分に高くない のでスカウト法の 仮定が正しくない場合が多く生じるため、null window search の後で αβ 法で計算の やり直しを行う必要がある回数が多いから だと考えられます。このように、move ordering の精度が低い場合 はスカウト法の効率は αβ 法よりも悪くなります。

一方、弱解決の AI である ai14s を利用して move ordering を行う場合は、ほとんどの場合でスカウト法と αβ 法の効率が 少しだけ悪化するかほとんど変わらない ことがわかります。その原因としては、以下のようなものが考えられます。

〇× ゲーム で計算する 評価値の範囲 が -1 ~ 1 や、-2 ~ 3 のように もともと狭い ため、ウィンドウ幅が 1 の null window search を行なっても ウィンドウ幅がほとんど狭くならず、枝狩りの 効率が変わらないか、ほとんど向上しない
ai14s は 強解決の AI ではない ので、いくつかのノード で先頭の子ノードの評価値が最大値にならず、null window search の後の やり直しを行う必要が何回か生じる

また、枝狩りは枝狩りを行ったノードの すべての子孫ノードが対象となる ので、一般的にはゲーム木の深さ 深い程効果が高まります。〇× ゲームのゲーム木の深さは 9 であり あまり深くない ので、それが原因で多くのノードでスカウト法による効率の上昇が得らなかった可能性が考えられます。

一般的なスカウト法の効率

上記の結果から、残念ながら 〇× ゲーム の場合は スカウト法による効率の上昇は得られない ことがわかりましたが、move ordering の精度が高ければ スカウト法が多くのゲームで有効であることが確認 されています。例えば、Wikipedia のスカウト法に関する記事には「チェスプログラムではアルファ・ベータ法に比べ、典型的には10％程度のパフォーマンス上昇が見込めると言われる」と記述されています。また、将棋の AI などでもスカウト法を利用することで効率の上昇が見込めるようです。

精度が 100 % の move ordering の場合のスカウト法

move ordering の精度が 100 % であれば、2 番目以降の すべての子ノード の null window search の結果が max ノードでは fail low、min ノードでは fail high になるため、αβ 法での計算のやり直しを行う必要が生じません。そのため、その場合は 必ず αβ 法以上の効率 で計算を行うことができます。

精度が 100 % の move ordering は 強解決の AI を利用することで行なえるので、強解決の AI である ai_gt6 を使った move ordering を行う下記のプログラムでそのことを確認することにします。なお、先頭の子ノードが最善手を着手したノード であれば move ordering の精度が 100 % になる ので、以下の処理では 先頭のみの move ordering を行う ことにします。また、ai_gt6 を利用する際には、局面と最善手の対応表のデータが必要 となるので、そのデータを load_bestmoves を使ってファイルから読み込んでいます。

from util import load_bestmoves
from ai import ai_gt6

bestmoves_by_board = load_bestmoves("../data/bestmoves_by_board.dat")
params = {"bestmoves_by_board": bestmoves_by_board}
for ai_for_mo in [ai_gt6]:
    for shortest_victory in [False, True]:
        for use_tt in [False, True]:
            for init_ab in [False, True]:
                print(f"ai_for_mo: {ai_for_mo}, sv: {shortest_victory}, init_ab: {init_ab}, use_tt: {use_tt}")
                count = 0
                count2 = 0
                for mb in mblist:
                    count += ai_abs_all(mb, ai_for_mo=ai_for_mo, params=params,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
                                        calc_score=True, calc_count=True)
                    count2 += ai_scout(mb, ai_for_mo=ai_for_mo, params=params,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
                                        calc_score=True, calc_count=True)
                print("abs count=", count)
                print("scout count=", count2)

実行結果

ai_for_mo: <function ai_gt6 at 0x0000016BFAD0AB60>, sv: False, init_ab: False, use_tt: False
abs count= 13151
scout count= 13151
ai_for_mo: <function ai_gt6 at 0x0000016BFAD0AB60>, sv: False, init_ab: True, use_tt: False
abs count= 8225
scout count= 8225
ai_for_mo: <function ai_gt6 at 0x0000016BFAD0AB60>, sv: False, init_ab: False, use_tt: True
abs count= 10035
scout count= 10035
略

強解決の AI である ai_abs_tt4 などの、αβ 法を利用した AI を move ordering を行うために利用することもできますが、ai_abs_tt4 はゲーム木を探索する必要があるため、局面と最善手の対応表を使って最善手を選択する ai_gt6 と比べて計算速度がかなり遅く、上記のプログラムの実行時間がかなり長くなってしまうという問題があります。興味がある方は実際に確認してみて下さい。

なお、余談ですが ai_gt6 は最善手のみを計算する機能しか持たないので、ai_gt6 を使って全ノードの move ordering を行うことはできません。また、ai_gt7 はすべての子ノードの評価値を計算する機能を持ちますが、× の手番では評価値の低いほうが × が有利になるという評価値を計算するので ai_scout で ai_gt7 を使って全ノードの move ordering を行うことはできません。

下記は実行結果をまとめた表です。実行結果から、最短の勝利を目指さない場合 は、下段の スカウト法の結果 と上段の αβ 法の結果が全く同じ であり、枝狩りの効率が変わらない ことが確認できます。

なお、下記の表では 最短の勝利を目指す場合 は 結果が同じになりません が、それには上記のプログラムでは最短の勝利を目指す際の move ordering の精度が 100 % ではないから です。その理由については後で説明しますが、余裕がある方は考えてみて下さい。

	ab × tt ×	ab 〇 tt x	ab × tt 〇	ab 〇 tt 〇
最短の勝利を目指さない	13151 13151	8225 8225	10035 10035	6080 6080
最短の勝利を目指す	14404 14389	13215 13345	10634 10590	9691 9670

前回の記事で 筆者が スカウト法が 下記のような性質を持つと誤解していた と書きましたが、実際にスカウト法を下記のように誤解している人は多いのではないかと思います。

move ordering の精度が 100%で、先頭の子ノードの評価値が最も高い場合にスカウト法の効率が αβ 法と比較して最も高くなる。

上記の説明は 間違っている ので赤い背景色のノートにしました。

また、Wikipedia のネガスカウト法の説明には以下のような記述があり、この記述からスカウト法が上記のような性質を持っていると誤解した人が多いのではないでしょうか？

「NegaScout が効率よく機能するかどうかは手の並べ替えの精度に依存しており、初めに調べる手が最善手である場合に最も効率が良くなる」

しかし、上記の実行結果からわかるように、move ordering の精度が 100% の場合は αβ 法とスカウト法の効率は全く同じ になります。筆者は ai_scout に何かのバグがあるため上記のような結果になったのではないかと最初は思っていたのですが、色々と考えた結果、ai_scout は正しい処理が行っていることがわかりました。

move ordering の 精度が 100 % の場合 に αβ 法とスカウト法の 効率が同じになる理由 は、精度が 100 % の場合はどちらも全く同じ処理を行う からです。同じ処理が行われる理由と、スカウト法がどのような場合に枝狩りの効率を上昇させるかについては次回の記事で説明します。余裕がある方はその理由について考えてみて下さい。

今回の記事ではこのような 誤解が起きた理由 についての 筆者の考察 を説明します。筆者と同じ誤解をしていた人は、上記のような誤解が生じる原因について少し考えてみて下さい。

誤解の原因の考察

上記のような誤解が起きる原因について考えてみたのですが、スカウト法が以下のような性質を持つからではないかと思います。

前回の記事で説明したように、スカウト法 は それまでに計算したノードの評価値 が子ノードの評価値の 最大値である²という仮定 をたて、その 仮定が正しい場合 に null window search によって 枝狩りの効率が高くなるよう工夫 したアルゴリズムです。

また、仮定が正しいかどうかによって、2 番目以降の子ノードの評価値を計算する際の効率 が αβ 法と比較 して以下のようになります。

仮定が 正しい場合 は効率が 同じか良くなる
仮定が 間違っている場合 は 効率が悪くなる

仮定が正しい子ノード によって得られた 効率の改善の合計 を $\boldsymbol{A}$、仮定が間違っている子ノード による 効率の悪化の合計 を $\boldsymbol{B}$ と表記した場合に、αβ 法と比較した際の 全体の効率の差 は $\boldsymbol{A - B}$ となります。従って、$\boldsymbol{A > B}$ の時にスカウト法のほうが αβ 法よりも 効率が良くなり、$\boldsymbol{A < B}$ の場合はスカウト法のほうが 効率が悪くなります。

B の性質の考察

スカウト法では 仮定が間違っている場合 は、null window search を行う必要がある 分だけ必ず効率が悪く なります。move ordering の 精度が高い程 仮定の 間違いが少なくなる ので、$\boldsymbol{B}$ は 仮定が間違っている子ノードが多い程大きく なり、move ordering の 精度が 100% の場合 は間違った仮定の子ノードが存在しなくなるため $\boldsymbol{B = 0}$ で 最小となります。

A の性質の考察

先程の〇× ゲームでの効率の比較では残念ながらスカウト法のほうが αβ 法よりも効率が高いという実例を示すことはできませんでしたが、先程説明したように、スカウト法の Wikipediaには、チェスでは実際にスカウト法のほうが αβ 法よりも 10 % 程度効率が高くなる という 実例が示されています。このことから、move ordering の精度が高ければ $\boldsymbol{A > B}$ となることが 実際にある ことがわかります。

また、move ordering の精度が低い と 仮定が正しい子ノードの数が減る ため、$\boldsymbol{A}$ が減る と考えられます。

上記の考察から、move ordering の精度 と $\boldsymbol{A}$、$\boldsymbol{B}$、$\boldsymbol{A - B}$ が以下のような関係を持つと考えた人は多いのではないでしょうか？

$\boldsymbol{A}$ は move ordering の 精度が 0 % の時に 0 となり、精度が 100 % の時に最大 になる
$\boldsymbol{B}$ は move ordering の 精度が 0 % の時に最大 となり、精度が 100 % の時に 0 になる
$\boldsymbol{A - B}$ は move ordering の 精度が 0 % の時に負の値の最小値 となり、精度が高くなるにつれ大きくなり、精度が 100 % の時に正の値の最大値 になる

上記の関係 を グラフで視覚化 すると下記のようになります。緑色の $\boldsymbol{A - B}$ のグラフの中で、効率の差が 0 であることを表す 灰色の横線より上になっている部分 が、スカウト法のほう が αβ 法よりも 効率が良い ことを表します。

上記のグラフでは便宜的に $\boldsymbol{A}$ と $\boldsymbol{B}$ の最大値を同じにしましたが、異なる最大値を持つようなグラフで視覚化してもかまいません。

上記のグラフから、先程の考察が正しければ move ordering の 精度が 100% の場合に $\boldsymbol{A - B}$ が最大となる ので、「move ordering の精度が 100% の場合にスカウト法の効率が αβ 法と比較して最も高くなる」事がわかりますが、実際にはそうはなりません。これは上記で示した $\boldsymbol{A}$ の性質の考察 のどこかが 間違っている からです。どこが間違っているかについて少し考えてみて下さい。

A の性質の考察の間違い

上記の考察で間違っているのでは、「move ordering の精度が低い程 と 仮定が正しい子ノードの数が減る ため、$\boldsymbol{A}$ が減る と考えられる」という部分です。この考察を行なった人はおそらく上記のグラフのように $A$ は move ordering の 精度が減ると 0 に向けて 常に減少（単調減少）していく と考えていたのではないかと思います。しかし、実際には $\boldsymbol{A}$ は move ordering の 精度が 100 % に近づくと 0 に向かって減る ようになり、精度が 100 % になると 0 になる という性質があります。そのため、move ordering の 精度が 100% の場合 は $\boldsymbol{A = B = 0}$ となるので、αβ 法とスカウト法の 効率が同じ になります。

このことをグラフにすると以下のようになります。グラフからわかるように スカウト法が αβ 法よりも効率が高くなる可能性がある のは 特定の範囲の精度だけ（下図の場合は精度が 50 % 以上 100 % 未満の範囲）で、一定の精度を下回るとスカウト法の効率が下回り、100 % になると効率が等しく なります。

なお、上記のグラフは正確なグラフでは全くありません。実際には $\boldsymbol{A}$ と $\boldsymbol{B}$ がどのようなグラフになるかは、ゲーム木によって異なります。$\boldsymbol{A}$ が上記のグラフのように上に綺麗な凸のようなグラフになるとは限りませんし、$\boldsymbol{B}$ が直線になるとは限りません。また、上記のグラフでは精度が 50 % の所で $\boldsymbol{A - B}$ が 0 となっていますが、一般的にはもっと高い精度の所で 0 となります。

上記の説明で「スカウト法が αβ 法よりも効率が高くなる 可能性がある」と記述したのは、下記のグラフのような場合はスカウト法の効率が 常に αβ 法以下 になる場合があるからです。先程の〇×ゲームの効率の比較の結果から、〇× ゲームの場合はおそらく下記のグラフのようになっている可能性が高いでしょう。ただし、どのような場合でも move ordering の精度が 100 % の場合は効率が同じ になります。

スカウト法と move ordering の精度の関係

move ordering の精度が 100 % の場合に、αβ 法とスカウト法の効率ga
同じになるという事実から、スカウト法では move ordering の精度が 一定以上高ければ、効率の上昇がほぼ 0 になるため それ以上精度を高くしても意味がない のではないかと 錯覚した人がいるかもしれません が、それは 間違い です。その理由は、以下通りです。

move ordering の精度を高くすると αβ 法の効率は上昇する
move ordering が 100 % に近くなると αβ 法の効率との差はほとんどなくなるが、αβ 法の効率が上昇するということは スカウト法の効率も上昇する

先程のグラフでは move ordering の精度と αβ 法とスカウト法の効率の差をグラフにしましたが、move ordering の精度 と αβ 法とスカウト法の それぞれの効率 をグラフにすると下記のようになります。グラフから move ordering の精度を高くすると、最後は上昇速度が αβ 法に比べて緩やかになりますが、最大値に向かって 上昇し続ける ことが確認できます。

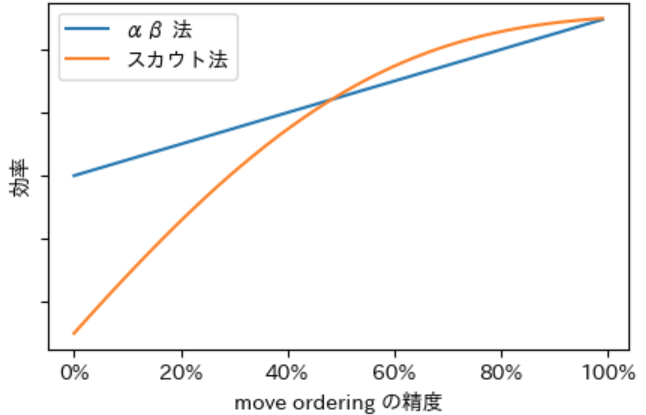
また、このグラフから、スカウト法は move ordering の精度が一定以上の場合に、αβ 法よりも低い move ordering の精度 で 最高の効率（100 % の move ordering での αβ 法）に より近い効率を得ることができるように工夫 したアルゴリズムであることがわかります。

上記のグラフも 正確なグラフでは全くありません。実際には $\boldsymbol{B}$ が上記のグラフのように直線になることはまずありませんし、$\boldsymbol{A}$ はもっと複雑な形になるでしょう。

上記をまとめると以下のようになります。

αβ 法もスカウト法も move ordering の精度を上げると効率が上昇する
αβ 法もスカウト法も move ordering の精度が 100 % の場合の効率は同じである
move ordering の 精度が一定以上の場合 に、スカウト法の方が αβ 法よりも 早く最大の効率に近づいていく ことが期待できる

move ordering の 精度が 100 % の場合 は αβ 法とスカウト法の効率が同じになるので、その場合は スカウト法を利用する必要がないのではないか と思う人がいるかもしれませんが、そのような心配をする必要はありません。その理由は 精度が 100 % の場合は move ordering だけで最善手を計算できる ので αβ 法やスカウト法を利用する意味がない からです。

move ordering の精度が 100 % の場合に αβ 法とスカウト法が同じ処理を行うことを示した論文がないか探してみたところ、Trends in Game Tree Searchという論文で以下のように言及されていました。

「On the other hand, if the tree would be perfectly ordered again NegaScout and Alpha-Beta would search the same subtree」

以下は、筆者による上記の意訳です。

一方、ゲーム木が完全（100 % の精度）に並べ替えられていた場合は、ネガスカウト法と αβ 法は再び同じ部分木を探索する（同じ枝狩りの処理を行う）ようになる。

なお、他にもこのことを言及している論文や文献があるかもしれません。

ChatGPT に「move ordering が完ぺきな場合に、同じ move ordrering を行った場合はスカウト法は αβ 法よりも効率がどれくらい良くなりますか？」と質問した所、長い答えの中で「完璧な move ordering がある場合、Scout 法は αβ 法よりもさらに少ないノード数で済むことがあります」という筆者と同じ誤解の回答が返ってきました。その後それは違うのではないかという質問をいくつかした所、誤解は無事に解けましたが、やはり生成 AI の回答を鵜呑みにするのは危険なようです。

Wikipedia 内での説明についての補足

先程紹介した Wikipedia の下記の説明 は、誤解を生じさせるような表現になっていると思いますが、厳密には間違ってはいない と思います。

「この様に NegaScout が効率よく機能するかどうかは手の並べ替えの精度に依存しており、初めに調べる手が最善手である場合に最も効率が良くなる」

その理由は、上記の説明の中に「αβ 法と比べて 効率が良くなる」とは 書いておらず、move ordering の 精度が高い程効率が良くなる のは事実だからです。

ただし、スカウト法 は αβ 法の効率を高めるため に考え出された手法なので、スカウト法の効率について言及した場合は αβ 法と比べてどれくらい効率が良くなっているか について言及していると 考えるのが自然ではないか と思います。上記の Wikipedia の説明から、最終的にスカウト法の効率が αβ 法と同じになると思った人はほとんどいないのではないでしょうか？これが筆者が上記の説明が誤解を生じさせるような表現であると考える理由です。

最短の勝利を目指す場合の検証

下記は先ほどの move ordering の精度が 100 % の場合の効率の比較結果の再掲です。

	ab × tt ×	ab 〇 tt x	ab × tt 〇	ab 〇 tt 〇
最短の勝利を目指さない	13151 13151	8225 8225	10035 10035	6080 6080
最短の勝利を目指す	14404 14389	132157 13345	10634 10590	9691 9670

上記の結果では、最短の勝利を目指す場合 に αβ 法とスカウト法の効率が一致していません。この結果は 精度が 100 % の move ordering を行った場合に αβ 法とスカウト法の 効率が同じになる という先程の説明に 矛盾している ように思えるかもしれません。このようなことが起きる原因について少し考えてみて下さい。

そのようなことが起きる原因は、最短の勝利を目指す場合 は複数の最善手の中から 最短で勝利する合法手の評価値が最も高く なりますが、ai_gt6 は すべての最善手に対して同じ評価値を計算する ため、ai_gt6 による move ordering によって 最大の評価値を持つ子ノードが先頭に移動しない場合がある からです。

このように、move ordering の精度 は、強解決の AI を利用すれば常に 100 % となるわけではありません。move ordering を行う AI は、決着がついた局面に対して計算される評価値に合ったものにする必要がある 点に注意が必要です。

最短の勝利を目指す場合は、下記のプログラムのように 最短の評価値を計算する場合の最善手を記録したファイル（bestmoves_by_board_shortest_victory.dat）を利用する必要があります。なお、下記では先ほどと異なり最短の勝利を目指す場合のみの計算を行っています。

bestmoves_by_board = load_bestmoves("../data/bestmoves_by_board_shortest_victory.dat")
params = {"bestmoves_by_board": bestmoves_by_board}
for ai_for_mo in [ai_gt6]:
    for shortest_victory in [True]:
        for use_tt in [False, True]:
            for init_ab in [False, True]:
                print(f"ai_for_mo: {ai_for_mo}, sv: {shortest_victory}, init_ab: {init_ab}, use_tt: {use_tt}")
                count = 0
                count2 = 0
                for mb in mblist:
                    count += ai_abs_all(mb, ai_for_mo=ai_for_mo, params=params,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
                                        calc_score=True, calc_count=True)
                    count2 += ai_scout(mb, ai_for_mo=ai_for_mo, params=params,
                                        shortest_victory=shortest_victory,
                                        init_ab=init_ab, use_tt=use_tt,
                                        calc_score=True, calc_count=True)
                print("abs count=", count)
                print("scout count=", count2)

実行結果

ai_for_mo: <function ai_gt6 at 0x0000016BFAD0AB60>, sv: True, init_ab: False, use_tt: False
abs count= 11106
scout count= 11106
ai_for_mo: <function ai_gt6 at 0x0000016BFAD0AB60>, sv: True, init_ab: True, use_tt: False
abs count= 9718
scout count= 9718
ai_for_mo: <function ai_gt6 at 0x0000016BFAD0AB60>, sv: True, init_ab: False, use_tt: True
abs count= 8955
scout count= 8955
ai_for_mo: <function ai_gt6 at 0x0000016BFAD0AB60>, sv: True, init_ab: True, use_tt: True
abs count= 7706
scout count= 7706

実行結果をまとめた表は省略しますが、上記の実行結果から、move ordering の精度が 100 % の場合は 最短の勝利を目指す場合 でもスカウト法と αβ 法の 効率が同じ になることがわかります。

今回の記事のまとめ

今回の記事ではスカウト法の実装を行い、いくつかの条件で αβ 法の効率と比較しました。また、直観に反して move ordering の精度が 100 % の場合に αβ 法とスカウト法の効率が同じになることを示しました。

次回の記事では move ordering の精度が 100 % の場合に αβ 法とスカウト法の効率が同じになる理由について説明します。

本記事で入力したプログラム

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル
ai.py	本記事で更新した ai_new.py

次回の記事

近日公開予定です。

24 行目の処理は 22 行目の β 値 ≦ $s$ の条件式が False の場合に実行されるので α 値 < $s$ を判定するだけでかまいません ↩
これは max ノードの場合で、min ノードの場合は最小値であるという仮定をたてます ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その166 スカウト法の実装と効率

目次と前回の記事

これまでに作成したモジュール

スカウト法の実装と効率の確認

null window search に関する補足

今回の記事で利用する記号

スカウト法のアルゴリズム

ネガスカウト法

ai_scout の定義

スカウト法の効率の確認

一般的なスカウト法の効率

精度が 100 % の move ordering の場合のスカウト法

誤解の原因の考察

B の性質の考察

A の性質の考察

A の性質の考察の間違い

スカウト法と move ordering の精度の関係

Wikipedia 内での説明についての補足

最短の勝利を目指す場合の検証

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その166　スカウト法の実装と効率

`ai_scout` の定義