LoginSignup
119
113

More than 5 years have passed since last update.

@ysdyt(ysdyt)inBrainPad Inc.

Pythonで「線形回帰」と"確率版の線形回帰"である「ベイズ線形回帰」

Last updated at Posted at 2016-09-25

モチベーション

  • Pythonで機械学習アルゴリズムを1から書く系のことがしたい
  • 「機械学習」でググると評判の良い技評のページがあり勉強を兼ねて。古いページですが、解説がわかりやすかったので読んだこと無い方はオススメです。
    • 以下、上記ページの自己理解のための再まとめです（詳細は文末に記載したオリジナルページを参照してください）

線形回帰の求め方の流れ

基底関数

  • 「線形回帰」では，まず「基底関数」というものを定める
    • 文字通り、関数を表現するベースとして使うもの
    • 基底関数に特別な条件はないので自由に好きな関数が使える
      • ただし、選び方によってモデルの性能や得られる関数の形などが決まるので、基底関数は解きたい問題にあわせて選ぶ必要がある
    • 中でもよく使われる基底関数2種類が以下（それぞれの詳細は後述）

多項式基底

\phi_i(x)=x^i\hspace{1.0em}(i=0,\cdots,M-1)

ガウス基底

\phi_i(x)=\exp\left\{-\frac{(x-c_i)^2}{2s^2}\right\}\hspace{1.0em}(i=0,\cdots,M-1)

線形回帰の求め方

  • 基底関数は最初に決めて固定し、その線形和を求めたい関数 f(x) とする
  • 各基底関数に与えられる重み$w_i$をパラメータとすることで、「想定する関数の集合」を得る
f(x)= \sum^{M-1}_{i=0}w_i\phi_i(x) = w^T\phi(x) \hspace{1.0em} （式1）
  • パラメータ$w_i$を決定すれば f(x) が求まるので、$w_i$を適切に決める方法があればいい
    • =>誤算関数として二乗誤差を使う
E(w)=\frac{1}{2}\sum^N_{n=1}(f(x_n)-t_n)^2 
=\frac{1}{2}\sum^N_{n=1}\left(\sum^{M-1}_{i=0}w_{i}x^{i}_{n}-t_n\right)^2 \hspace{1.0em} （式2）

  • 一見複雑だが、$x_n$と$t_n$が定数（すでに与えられている点）であることを思い出せば，これは$w_i$の関数とみなすことができ、単なる$w_i$の二次式である

    • したがって、誤差関数$E(w)$を最小にする$w_i$を求めることができて、求めたい関数 f(x)も決めることができる

  • 重み$w$を二乗誤差の最小化で求めることが「線形回帰」の基本的な流れ

サンプルデータ

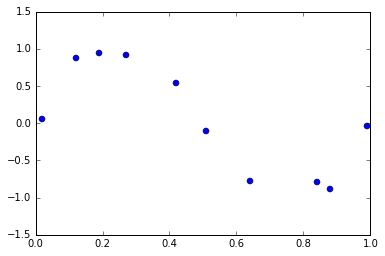
以下のようなプロットが与えられた時、その線形回帰を求めたい

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

X = np.array([0.02, 0.12, 0.19, 0.27, 0.42, 0.51, 0.64, 0.84, 0.88, 0.99])
t = np.array([0.05, 0.87, 0.94, 0.92, 0.54, -0.11, -0.78, -0.79, -0.89, -0.04])

plt.xlim([0,1.0])
plt.ylim([-1.5,1.5])
plt.plot(X, t, 'o')
plt.show()

output_3_0.png

このXとtの関係を線形回帰で求める

多項式基底を使って線形回帰を求める

多項式基底

以下の式で定義される（再掲）

\phi_i(x)=x^i\hspace{1.0em}(i=0,\cdots,M-1)

  • 多項式基底は、見慣れた"多項式"という形式で解を得られるというメリットの反面、データが離れた点での推定に影響を強く及ぼすという特徴がある

    • 解の表記に対する制約が強すぎる、という言い方もできる

  • 今回は特徴関数φに三次関数の多項式基底を用いて解いてみる。そのため求めたい回帰式 $f(x)$ は以下となる

f(x)=w_{1}+w_{2}x+w_{3}x^2+w_{4}x^3
  • 基底関数φ(x)を固定しつつ、パラメータ$w$は自由に動かします
  • そうすると $f(x)$ が変化するので、その中で「与えられたデータ点に一番適した$w$」を見つけるのが線形回帰のアプローチ
  • $f(x)$がデータ点 ($X_n$,$t_n$) (n=1, ..., N) の「一番近く」を通るような$w$は、『誤算関数$E(w)$が最小となる$w_i$では偏微分が0になる』ことを使って、最小値を与える$w_i$を求める
\frac{\partial E(w)}{\partial w_m}=\sum^N_{n=1}\phi_m(x_n)\left(\sum^M_{j=1}w_j\phi_j(x_n)-t_n\right)=0 \hspace{1.0em}(m=1,\cdots,M) \hspace{1.0em} （式3）
  • 行列を使ってこの連立方程式を整理すると，解$w$は以下式で求められる
w = (\phi^T\phi)^{-1}\phi^{T}t \hspace{1.0em} （式4）

ただし、Φは以下のように定義される行列となる

    \phi=\left(
    \begin{array}{ccc} 
        \phi_{1}(x_1) & \phi_{2}(x_1) & \cdots & \phi_{M}(x_1)  \\ 
        \vdots & \vdots& & \vdots      \\ 
        \phi_{1}(x_N) & \phi_{2}(x_N) & \cdots & \phi_{M}(x_N)\\ 
    \end{array}  
    \right) \hspace{1.0em}（式5）
  • こうして求めたパラメータ$w$を$f(x)= \sum^{M-1}_{i=0}w_i\phi_i(x) = w^T\phi(x)$に代入すると，データ点の近くを通る関数$f(x)$が得られる

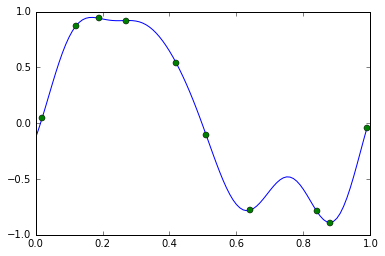
多項式基底（三次関数）で線形回帰を求める（上記内容の実装）

上記の内容をそのままコードに書き下して、多項式基底（三次関数）で線形回帰を求める
（※ここでは正規化項などは考えない）

# 特徴関数φに多項式基底を用いた場合
def phi(x):
    return [1, x, x**2, x**3]

PHI = np.array([phi(x) for x in X])
#上記の（式4）部分の計算。np.dot:内積を求める　np.linalg.inv:逆数を求める
w = np.dot(np.linalg.inv(np.dot(PHI.T, PHI)), np.dot(PHI.T, t))
#連立方程式の解を求めるのにnp.linalg.solve関数も使える。こちらのほうが高速。np.linalg.solve(A, b): A^{-1}b を返す
#w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, t))

xlist = np.arange(0, 1, 0.01) #線形回帰の式のx点。 0.01単位で細かくプロットし、線として出力させる
ylist = [np.dot(w, phi(x)) for x in xlist] #線形回帰の式のy

plt.plot(xlist, ylist) #線形回帰式のプロット
plt.plot(X, t, 'o')
plt.show()

output_8_0.png

#上記の計算で得られたwを出力する
w

array([ -0.14051447,  11.51076413, -33.6161329 ,  22.33919877])

つまり、線形回帰の結果として$f(x)=-0.14+11.5x-33.6x^2+22.3x^3$という回帰式が得られた

ガウス基底を使って線形回帰を求める

ガウス基底

ガウス基底は以下の式で定義される釣り鐘型の関数（分布ではない）

\phi_i(x)=\exp\left\{-\frac{(x-c_i)^2}{2s^2}\right\}\hspace{1.0em}(i=0,\cdots,M-1)\hspace{1.0em}（式6）
  • ガウス基底は、データ点の近くはその情報を強く使って、離れるにしたがって影響を弱めるというモデル
  • 「観測されたデータには，あるランダムなノイズが足されている」という考え方をベースにしている
    • 「観測値のずれ具合（ランダムなノイズ）は正規分布に従う」と仮定して説明する

ガウス基底の変数s

  • $s$はデータが影響を及ぼす距離をコントロールするパラメータ（ガウス基底は分布ではないが、$s$は正規分布でいうところの分散みたいなイメージ（たぶん））
    • 大きくするほど遠くまで影響が届くようになる。そのため小さめの値が望ましい
    • しかし、あまり小さくするとデータの密度が低い箇所でどのデータ点も使えず正しく推論ができないということが起こる
  • 今回は$s$=0.1として実行してみる

ガウス基底の変数c_i

  • $c_i$はガウス基底の中心を表す
    • このガウス基底の線形和で求めたい関数を表すので、回帰を行いたい区間をカバーするように取る必要がある
    • 基本は先ほどの$s$に設定した値の間隔で取っていけばok
  • 今回は0〜1区間から$s$=0.1間隔で取った11個のガウス基底関数を使ってみる

ガウス基底で線形回帰を求める（上記の内容の実装）

まずは単純に、上記の線形回帰で用いた特徴関数φを「多項式基底」から「ガウス基底」に書き換えた図を出してみる

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

X = np.array([0.02, 0.12, 0.19, 0.27, 0.42, 0.51, 0.64, 0.84, 0.88, 0.99])
t = np.array([0.05, 0.87, 0.94, 0.92, 0.54, -0.11, -0.78, -0.79, -0.89, -0.04])

# 特徴関数φにガウス基底を用いた場合
# phiは11個のガウス基底関数に加えて，定数項を表すための1を加えて12次元のベクトルを返す
# ガウス基底（0〜1.0まで0.1刻みの11地点）+定数項 1地点の計12地点（次元）を返す
def phi(x): 
    s = 0.1 #ガウス基底の「幅」
    # 式6の書き下し
    return np.append(1, np.exp(-(x - np.arange(0, 1 + s, s)) ** 2 / (2 * s * s)))

PHI = np.array([phi(x) for x in X])
w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, t))

xlist = np.arange(0, 1, 0.01)
ylist = [np.dot(w, phi(x)) for x in xlist]

plt.plot(xlist, ylist)
plt.plot(X, t, 'o')
plt.show()

output_14_0.png

12次元のガウス基底は4次元の多項式基底よりさらに自由度と表現力が高いため完全に過学習になってしまっている

線形回帰を確率化するベイズ線形回帰

  • 推定値$w$の意味の違い

    • 線形回帰　⇒ 基底関数の線形和の範囲で二乗誤差を最小とする係数wを求める
    • ベイズ線形回帰　⇒　事後確率が最大となる値を$w$の推定値とする

  • 確率化した線形回帰では、「観測されたデータにはあるランダムなノイズが足されている」という考え方をベースにしている

    • 「ランダムなノイズ」、つまり「ずれ具合」は下記式で正規分布で仮定された$N(t|\mu,\beta^{-1})$で定式化される
p(t|w,x) = N(t|\mu,\beta^{-1})=\frac{1}{Z}\exp\left\{-\frac{1}{2}\beta(t-\mu)^2\right\} \hspace{1.0em}（式7）\\
ただし、\mu=f(x)=\sum^M_{i=1}w_i\phi_i(x), Z=\sqrt{2\pi\beta^{-1}}

  • $N(\mu,\beta^-1)$は予測値 $\mu=f(x)$を中心に、離れるほど確率が低くなる分布

    • その低くなり具合は$\beta$によってコントロールされていて、$\beta$が大きいと中心に強く集まり、小さいとずれも幅広くなる
    • 分散の逆数であるこの$\beta$は「精度」ともよばれる
    • $\beta$は1以上の出来るだけ大きな値が好まれる

  • 上記の式7に点$（x_1,t_1）$を代入した場合、それによって得られる$w$の関数$p(t_1|w,x_1)$は「尤度関数」と呼ばれる

    • 確率版の線形回帰であるベイズ線形回帰では、尤度関数を最大にする$w$が最適なパラメータとして選ばれる

  • 各点における尤度の掛け算で確率が求まり、それを最大化する$w$を求められば良い

    • 掛け算は面倒なので尤度の対数を取る（対数尤度関数）。対数をとる前に最大となる$w$と対数をとった後に最大となる$w$は一致する。
      • つまり、式7の対数をとり整理した以下式8の最大値を得る$w$を求めれば良い
\ln{p(T|w,X)}=-\frac{1}{2}\beta\sum^N_{n=1}\left(t_n-\sum^{M}_{i=1}w_{i}\phi_i(x_n)\right)^2+C \hspace{1.0em} （式8）
  • 式の構造を見てみると式8は、二乗誤差を求めた式2と実質同じ
    • 符号が逆なのは、二乗誤差は「最小化」、対数尤度関数は「最大化」することに対応しているため
    • β(>0)やCはwを含まない定数項なので最大化に影響なし
    • つまり、式8を最大化する$w$は式4で解ける

事前分布p(w)から事後分布p(t|w,x)を求める

  • 事後分布$p(t|w,x)$の特にxは入力値なので定数扱いして$p(t|w,x)$も$p(t|w)$と表記する
    • $p(w)$とデータ点(x,t)を使って$w$の分布を事後分布$p(w|t)$に更新する。この事後分布が求めたい「答えの自信」となる。
    • 事後分布への更新式はベイズ公式と乗法・加法定理から得られる
p(w|t)=p(t|w)p(w)/p(t) \\
p(t)=\int p(t,w)dw=\int p(t|w)p(w)dw
  • 事前分布として平均が0、共分散行列が単位行列の定数倍という正規分布$p(w)=N(w|0,\alpha^-1I)$を仮定した場合、
    • 更新式 $p(w|t)=p(t|w)p(w)/p(t)$ にこのp(w)を代入し、式を整理すると以下が得られる（定数項は$\frac{1}{Z'}$と省略）（$\alpha$については後述）
p(w|t)=\frac{1}{Z'}\exp\left\{-\frac{1}{2}(w-m)^T\sum^{-1}(w-m)\right\} \hspace{1.0em} （式9）\\
ただし \\
m=\beta t\sum\phi(x)\\
\sum^{-1}=\alpha I+\beta\phi(x)\phi(x)^T
  • 式9の$\exp$の{ }内を見てみると、$ N(w|\mu,\sum)=\frac{1}{Z}\exp{(-(w-\mu)^{T}\sum^{-1}(w-\mu)}$ のexpの部分に一致している
    • つまり、$p(w|t)$のは$N(w|\mu,\sum)$だということが$Z'$を求めずともわかる
N(w|\mu,\sum)=\frac{1}{Z}\exp\left\{(-(w-\mu)^T\sum^{-1}(w-\mu)\right\}

p(w|t)=N(w|m,\sum)
  • 事前分布が正規分布であり、ここで得られた事後分布も正規分布であることからこれらは共役な事前分布として使える
    • N個のデータ点$x=(x_1,\cdots,x_N)^T,t=(t_1,\cdots,t_N)^T$に対しても，その事後分布$p(w|t,x)$を同じように求めることができる
    • つまり、以下のような正規分布となる
p(w|t,x)=N(w|m_N,\sum_N) \hspace{1.0em} （式10）  \\
ただし \\
m_N=\beta \sum_N\phi^{T}t\\
\sum^{-1}_N=\alpha I+\beta\phi^T\phi

※ $\phi$は式5と同じように定義される行列

  • 結果、まずデータ点$(x_1,t_1)$に対してその事後分布$p(w|t_1,x_1)$を求め、それをまた事前分布とみなし、別のデータ点$(x_2,t_2)$を使って次の事後分布$p(w|t_1,t_2,x_1,x_2)$を求めて…という操作を繰り返して得られる$p(w|t_1,…,t_N,x_1,…,x_N)$と同じ分布になる

  • 事後分布を求めたことで「ベイズ線形回帰を解いた」ことになる

    • $w$の事後分布$p(w|t)=N(w|\mu_N,\sum_N)$は正規分布なので、平均$\mu_N$を頂点とする釣り鐘型の分布になる
      • したがって一番「自信」のある、つまり一番確率の高い答えは$w=\mu_N$となる
        • 事後分布の最大点を$w$の推定値とみなす手法は、事後分布最大化（Maximum a Posterior，MAP）推定という
        • 「自信」の度合いは裾の広がり具合（共分散$\sum_N$）から知ることができる（後述）

ベイズ線形回帰の正則化

  • また、ベイズ線形回帰にも正則化のアイデアがあるが、
    • 上記の式10の$\sum_N$を$m_N$に代入すると正則化付きの線形回帰の係数$w$を得るのと同様の式が得られる
    • 線形回帰のベイズ化と正則化は同じ最適解を導くことがわかっている（詳細はこちらのページ）

ベイズ線形回帰の実装

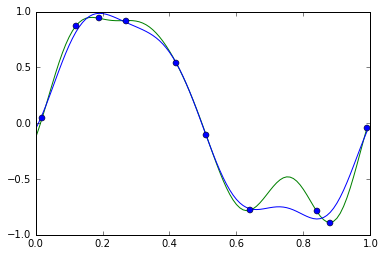
ベイズ線形回帰（青線）と普通の線形回帰（緑線）の両方をグラフに重ねて比較してみる

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

X = np.array([0.02, 0.12, 0.19, 0.27, 0.42, 0.51, 0.64, 0.84, 0.88, 0.99])
t = np.array([0.05, 0.87, 0.94, 0.92, 0.54, -0.11, -0.78, -0.79, -0.89, -0.04])

# 特徴関数φにガウス基底を用いた場合
def phi(x): 
    s = 0.1
    return np.append(1, np.exp(-(x - np.arange(0, 1 + s, s)) ** 2 / (2 * s * s)))

PHI = np.array([phi(x) for x in X])

# （上記と同じ）ガウス基底を用いたただの線形回帰を解く → 過学習してしまう
w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, t))

# ガウス基底を用いたベイズ線形回帰を解く → 過学習を回避
# 上記の式10の書き下し
alpha = 0.1 #仮置き
beta = 9.0  #仮置き
Sigma_N = np.linalg.inv(alpha * np.identity(PHI.shape[1]) + beta * np.dot(PHI.T, PHI)) #np.identity(PHI.shape[1])はガウス基底で指定した12次元の単位行列
mu_N = beta * np.dot(Sigma_N, np.dot(PHI.T, t))

xlist = np.arange(0, 1, 0.01) 
plt.plot(xlist, [np.dot(w, phi(x)) for x in xlist], 'g')     #普通の線形回帰の解をプロット
plt.plot(xlist, [np.dot(mu_N, phi(x)) for x in xlist], 'b')  #ベイズ線形回帰の解をプロット
plt.plot(X, t, 'o') #サンプル点をプロット
plt.show()

output_20_0.png

  • ベイズ線形回帰（青）は普通の線形回帰（緑）よりもうまく過学習を避けてプロットできている
    • ベイズ線形回帰では、事後確率が最大となる値をwの推定値としている。これは上記の最後に記したように、正則化付きの線形回帰の結果と一致する

共分散Σ_Nとはなんだったのか

  • 共分散$\sum_N$はそのデータ点の「確率の自信」を表していた
    • 一次元の分布の「分散」はデータの「散らばり具合」を表す
    • 一方、多次元の「共分散」は行列になるので、分散ほど簡単ではない
      • 今回の$\sum_N$でも12×12の行列となっている
#共分散行列Sigma_Nを見やすく表示
print "\n".join(' '.join("% .2f" % x for x in y) for y in Sigma_N)

 2.94 -2.03 -0.92 -1.13 -1.28 -1.10 -1.21 -1.14 -1.23 -1.06 -0.96 -2.08
-2.03  2.33 -0.70  1.95  0.13  1.02  0.85  0.65  0.98  0.70  0.65  1.44
-0.92 -0.70  2.52 -1.86  1.97 -0.29  0.42  0.59  0.13  0.40  0.32  0.63
-1.13  1.95 -1.86  3.02 -1.66  1.50  0.17  0.29  0.73  0.33  0.36  0.82
-1.28  0.13  1.97 -1.66  2.82 -1.11  1.39  0.22  0.55  0.49  0.40  0.92
-1.10  1.02 -0.29  1.50 -1.11  2.39 -1.35  1.72 -0.29  0.53  0.46  0.69
-1.21  0.85  0.42  0.17  1.39 -1.35  2.94 -2.06  2.39 -0.02  0.25  1.01
-1.14  0.65  0.59  0.29  0.22  1.72 -2.06  4.05 -2.72  1.43  0.37  0.67
-1.23  0.98  0.13  0.73  0.55 -0.29  2.39 -2.72  3.96 -1.41  1.23  0.59
-1.06  0.70  0.40  0.33  0.49  0.53 -0.02  1.43 -1.41  3.30 -2.27  2.05
-0.96  0.65  0.32  0.36  0.40  0.46  0.25  0.37  1.23 -2.27  3.14 -0.86
-2.08  1.44  0.63  0.82  0.92  0.69  1.01  0.67  0.59  2.05 -0.86  2.45
  • 共分散行列は対角行列であることがわかる
    • 対角成分
      • 対応するパラメータを単独で見た場合の分散を表す
      • つまり対角成分は一次元の正規分布の分散と同じ
        • 今回のデータでは一番小さいものでも2.33と，どの対角成分もあまり小さくない
          • データが少ないためパラメータ推定の精度があまり高くない可能性がある
    • 各要素同士が交差する点
      • 対応するパラメータ同士の相関を表す
        • 0だと相関なし（互いに独立）
        • 正の値だと片方が平均より大きいときはもう片方も平均より大きくなる傾向
        • 逆に負の値なら平均より小さくなる傾向
      • ガウス基底を使った今回のデータでは、
        • 定数項の係数（第1パラメータ）とそれ以外のパラメータ、および隣同士のガウス基底の係数は負の相関がある
        • 離れたガウス基底同士はおおむね正の相関があるがどれもだいたい弱い（0に近い）
  • 実際に問題を解くときは共分散行列をわざわざこのように眺めることはあまりない

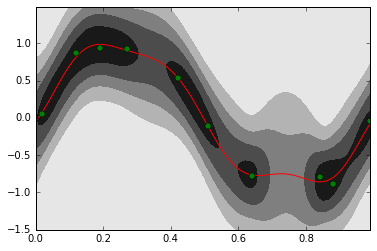
予測分布を可視化する

  • （アイデア的には、）事後分布$p(w|X)$とはパラメータwの分布なので、これを$p(y|w,x)$に「代入」すると，xを与えるとyの分布が返ってくる「関数」$p(y|X,x)$が得られる（本当は分布に分布を代入することはできないのであくまでもイメージ）

    • ターゲットとなる変数の分布に事後分布を反映させたものを予測分布と呼ぶ

  • 以下の予測分布の書き方の詳細はこちらを参照

# 正規分布の確率密度関数
def normal_dist_pdf(x, mean, var): 
    return np.exp(-(x-mean) ** 2 / (2 * var)) / np.sqrt(2 * np.pi * var)

# 2次形式( x^T A x を計算)
def quad_form(A, x):
    return np.dot(x, np.dot(A, x))

xlist = np.arange(0, 1, 0.01)
tlist = np.arange(-1.5, 1.5, 0.01)
z = np.array([normal_dist_pdf(tlist, np.dot(mu_N, phi(x)),1 / beta + quad_form(Sigma_N, phi(x))) for x in xlist]).T

plt.contourf(xlist, tlist, z, 5, cmap=plt.cm.binary)
plt.plot(xlist, [np.dot(mu_N, phi(x)) for x in xlist], 'r')
plt.plot(X, t, 'go')
plt.show()

output_26_0.png

  • 濃い部分は確率密度関数の値が高い、つまり推定される関数がそこを通る可能性が高い部分
    • データの密度が高いところは推定に自信があり、薄いところはデータ点の間隔が広いため推定に自信がない

事前分布のハイパーパラメータαについて

  • ベイジアンの事前分布$p(w)=N(w|0,\alpha^-1I)$に入っているパラメータは特にハイパーパラメータとも呼ばれる
  • αが大きいほど分散が小さくなる、つまりwが0に近い値だという事前知識が強くなる
    • この状態でベイズ線形回帰を解くと、wを0に近い値に推定しようとする力が強いため、いわゆる過学習しているような結果になるのが抑えられやすい反面、真の解にたどり着くまでに多くのデータを必要としてしまうかもしれない
    • 逆にαが小さいとwを押さえつける力が弱くなります
      • 特にαが0の時は普通の線形回帰と一致する。そこで0に近い小さめの値、例えば0.1や0.01あたりを設定してまずは解いてみることが多い

元ネタ

119
113
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
119
113