VAEの実装報告は多く見られるのですが、Conditional VAEに関しての実装の記事はまだあまり見かけません。生成モデルから出てくるランダムな結果を楽しむフェイズから一歩踏み込み、狙ったものを作る必要が出てきた際には必須の技術かと思いますので、Tensorflowにてトライしてみました。
概要
VAEの解説と実装は枚挙に暇がありませんので、ここでは割愛させていただきます。非常に詳しい説明が、http://nzw0301.github.io/notes/vae.pdf にまとめられておりますので、そちらを参照されるのが良いかと思います。
Conditional VAEは、画像などに添えて、label (=Condition)を同時に学習させることで、labelに対応した出力を得るネットワークを構築しようというものです。
Encoder, Decoderの双方に対して、labelの情報をone-hot vectorで与えてあげます。入れ方は自由だと思いますが、よく行われるのは下記です (ここでは、labelの次元数はNとします):
- Encoderでは、カラー画像3channelに加えて、labelのone-hot vectorに対応するfeatureを追加してあげます。結果として、入力画像の時点でfeatureは、N+3となります
- Decoderでは、latent vector zにconcateneteする形で、labelのone-hot vectorを追加してあげます
上記を行うことで、Encoder, Decoder双方、labelの情報を知ることができます。
通常、latent vector zは正規分布状のノイズに従って振られています。その中でも、再構成後の画像をできるだけ元の画像に近づけようとすると、Decoderとしては変動を受けないlabel vectorに基づいて概形を決定する方が確実ですので、概形をそちらから構成するようになります。
またEncoderは、latent vector zは相互に無相関の正規分布としなくてはいけませんので、いつも共通の成分となるものは、labelの情報を参照しながら除いてしまうことが必要です。
概念的には、上記のような考え方で、単にlabelの情報を与えるだけで、Encoder,Decoder双方がlabelを踏まえた出力を出すようになります。
実装上の留意点
実装自体は、githubにアップロードしております:
https://github.com/ysasaki6023/conditionalVAE/tree/v1.0
以下に、いくつか実装上の留意点を示します。
入力画像の規格化
必ず0-1になるよう正規化を行う必要があります。これは、loss関数としてベルヌーイ関数を使用しており、これが0-1にて定義されているためです。これを外れると、多くの場合、まともな結果を生成できません。
一方、画像として出力する際には、255を掛けて本来の数値に戻してあげる必要があります。
Decoder最終層をsigmoid(x)にて正規化
同様に、Decoderの最終層もsigmoid(x)として、0-1の範囲に正規化を行う必要があります。
$\tanh(x)$だと、-1~+1の範囲になってしまうので気をつけてください。
この正規化を間違えると、ベルヌーイ関数がおかしくなり、optimizeの中で突然大きな負のlossなどを出力します。
sigmaの定義
Encoderの出力には、latent vectorを設定するためのsigmaが含まれます。ただ、これが負の値をとってしまうと、lossの計算で破綻しNaNとなってしまいますので、注意が必要です。
対策として、正負を取れる変数$a$を使って、以下のように定義します:
$$
\sigma = \exp(a)
$$
こうすることで、aは正負どちらの値をとったとしても、$\sigma$は正となります。
Reconstruction Loss関数をベルヌーリ関数にて定義
Decoderの出力を教示画像と比較し、ロスを計算する際にどのような関数を使用するかには自由度があり、RMSを使用している実装もいくつか見受けられます。通常のAuto-EncoderにKL-divergenceを加えた拡張だと見ている人に、多い傾向です。
ただ下のオリジナルの式 ( https://arxiv.org/pdf/1312.6114.pdf ) から見ると、ここは確率を計算してロスとするところですし、次に述べるKL-divergenceとのバランスも正しく取り扱うためには、ベルヌーイ関数を使用するのがベターです。
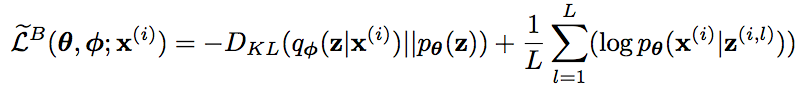
ベルヌーリ関数は、ピクセル毎に見たときに、教示 xとdecoder出力 p を用いて、
$$
B(p,x) = p^x + (1-p)^{(1-x)}
$$
と書けます。Gray scaleの場合xは連続値ですが、白黒の場合は0 or 1になります。また、実際のロスの定義では、このlogを取る必要があることに注意してください。
KL-divergenceの定義
オリジナルの論文 ( https://arxiv.org/pdf/1312.6114.pdf ) を参照すると、下記のように書かれています。
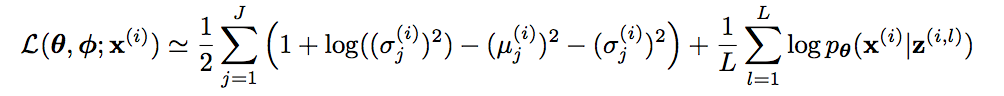
同様の計算を提示している別の論文/web記事もあるのですが、たまに$\sigma$ではなく、$\Sigma$として書かれている場合があります。これは単に文字の違いだけではなく、自乗分の違いがありますので、注意が必要です。
結果
MNISTの手書き文字を学習させました。0-9の数字をlabelとしています。
最終的には、250k ✕ 64枚/バッチ 分のデータを学習させていますが、約30分程度の時間でした。実際には、15k ✕ 64枚/バッチ 程度の時点で十分に学習は完了していましたので、ちょっとやりすぎたかもしれません。
ちなみに 15k ✕ 64 / 50k = 20 epochになります。
labelを指定し、latent vector zは正規乱数
このセットアップの場合、流石にlatent vector zが可読性の低い領域になる可能性も捨てきれず、下図のように一部は汚い文字が生成されることもあります:
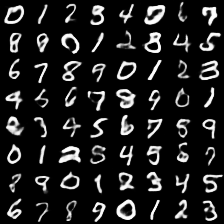

labelを指定し、latent vector zは定数
まともなlatent vector zを一つ選び、それに対応するlabelを指定すると、フォントのスタイルを共通に保ったまま、一連の数字を作り出すことができます:
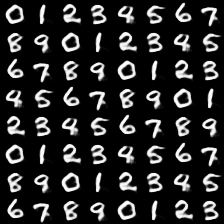

太い・細い筆致を保ったまま、異なる文字が生成されていることがわかります。