背景
かつて、モナコのあるカジノを破産させたと伝えられる「カジノの必勝法」がある。
その名も「モンテカルロ法」。
※Qiita民の間では、シミュレーションや数値計算を乱数を用いて行う手法としての
「モンテカルロ法」は高名であるが、それとは同姓同名の別人(別法?)。
「カジノの必勝法」の中で、最も有名なものは、
「マーチンゲール法」だろう。
倍々に賭けていって、いつかは当たるので必ず勝てる、という戦略。
倍々にすると、どこかで資金的orルール的な掛け金の上限に達するため、
これは必勝法とは言えない、とすぐに分かる。
一方、「モンテカルロ法」は、はるかに優秀な戦略で、実用的だ。
内容を聞けば、カジノを破産させたという伝説にも、説得力がある(かもしれない)。
「東京カジノ」でも「ラスベガス」でも「マカオ」でも、
または、株や仮想通貨の取引においても使える(かもしれない)。
結論から言えば、本稿においても、
勝率97% というシミュレーション結果が出た。
※ここまで見てカジノに直行せずに、最後まで熟読すること
この記事の概要
この記事は、「モンテカルロ法」の伝説の秘密を解き明かすべく、
chart.js を使って、勝ち負けのシミュレーション結果を
グラフ表示するアプリ(Webサイト)を作った物語である。
実際に読者にも動かせる形で、そのシミュレータも公開する。
本稿は、 クソアプリ Advent Calendar 2018 の24日目の「代打投稿」。
「伝説」に挑むクソアプリ(実用性は無い)を作った物語。
かつて、多くの男たちが、
カジノの必勝法を編み出し、そして破産していった。
同じような運命を辿る前に、ぜひ本稿で、
「伝説的カジノの必勝法」を心ゆくまで試してほしい。
また、chart.jsの他のサンプルも提示するので、
JavaScriptでHTML上に綺麗なグラフを書く、ことの
実戦的サンプルとしても見ていただけるかもしれない。
最後に、コードの主要部分も掲載しておく。
最近は言葉の真意を理解しない人も多いので、誤解が生じないように、
大真面目な語りで盛大にボケる話だと予め宣言しておく。
※カジノに行く場合は必ず自己責任で賭けてくださいね。
モンテカルロ法とは?
まず最初に、「モンテカルロ法」はどうして必勝法なのか、
戦略と、必勝である理由を説明する。
モンテカルロ法の戦略
賭ける対象は、ルーレットの赤黒のような、
勝てば倍になるゲームを例として説明する。
- 儲けたい金額を10$とする
- 合計が10になるように数字を書く
- [1, 2, 3, 4]
- 両端の合計の数を賭ける(今回は「1」+「4」)
- 勝った場合は、その両端の数字を消去
- ⇒[2, 3]
- 負けた場合は、今回賭けた金額を右端に追記
- ⇒[1, 2, 3, 4, 5]
- これを繰り返して、数字を全て消したら終了
- もし途中で数字が一つ残った場合は、分割する
- 例:[5] ⇒ [2, 3]
なぜ「必勝」なのか?
「数字のリストの合計」=「目標金額」と常に等しい、と気がつく。
つまり、全ての数字が消えれば目標達成になる。
勝った場合 ⇒ 数字が2つ減る
負けた場合 ⇒ 数字が1つ増える
50%で勝つ勝負ならば、
平均すれば、必ず数字の個数を減らしていくことができる。
つまり、必ず目標を達成することができる。
「負けたら倍賭け」の「マーチンゲール法」と違うのは、
負け続けた場合でも、掛け金の上昇がかなり緩やかであることだ。
「マーチンゲール法」では、
「破産リスク」や「カジノの最大賭け金の設定」が壁になるが、
「モンテカルロ法」は現実的に勝利(10$獲得)できる!
※ここまで見てカジノに直行せずに、最後まで熟読すること
(繰り返し)
賭けの進行例
- [1, 2, 3, 4] ⇒ 5賭けて負け
- [1, 2, 3, 4, 5] ⇒ 6賭けて勝ち
- [2, 3, 4] ⇒ 6賭けて負け
- [2, 3, 4, 6] ⇒ 8賭けて負け
- [2, 3, 4, 6, 8] ⇒ 10賭けて負け
- [2, 3, 4, 6, 8, 10] ⇒ 12賭けて勝ち
- [3, 4, 6, 8] ⇒ 11賭けて負け
- [3, 4, 6, 8, 11] ⇒ 14賭けて勝ち
- [4, 6, 8] ⇒ 12賭けて勝ち
- [6] ⇒ [3, 3](数字が一つなので分割)
- [3, 3] ⇒ 6賭けて勝ち
- [] ⇒ 結果10$の儲け!!
もし、マーチンゲール法だと、10$儲けようとすると、
3連敗後に1勝の場合、最後の掛け金は80$賭けることになる。
上の進行例で、3連敗している箇所があるが、
掛け金の増加がはるかに緩やかであることが確認できる。
最強の方法じゃん!?これで私も大金持ち!?
実際のカジノでは、「メモ」が禁じられている場合が多いという点を除けば、
一見、非の打ちどころがない方法に見える。
数字の個数で考えれば、基本的には減ってゆくはずだし、
負け続けても掛け金が倍々的に増えることは無い。
そこで、本稿では、
「モンテカルロ法のシミュレータ」を開発し、
その性能を試してみることにした。
自分で先に試したい方
↓↓↓
このページ の「必勝法を試す」から。
↑↑↑
※他にも**「ガチャ」の2%の当たりは100回引いて出るのか?**などが
試せるシミュレータが用意されている。
なお、前提として、「控除率」は0%とした。
「破産」まで行く前に「カジノの最大賭け金の設定」に
引っ掛かるものとして、最大賭け金を設定できるものとした。
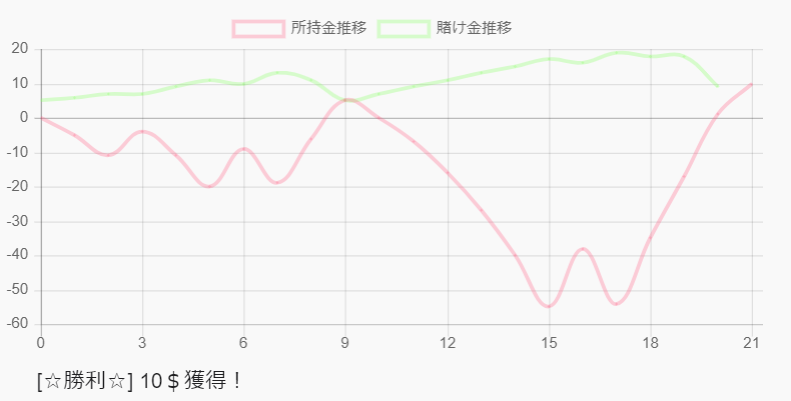
シミュレーション結果①
chart.jsを使て、所持金と賭け金のグラフを作成できる。
上の例では、勝ったり負けたりしているが、賭け金は最大でも20$いかずに、
最終的には10$の儲けを得て、21回で勝利している。
上の例も、最終的には勝利した図。
通常は、もっと簡単に10$獲得して終わり、というシンプルな図になることが多い。
(四分の一の確率で、最初に2連勝して終わりになる)
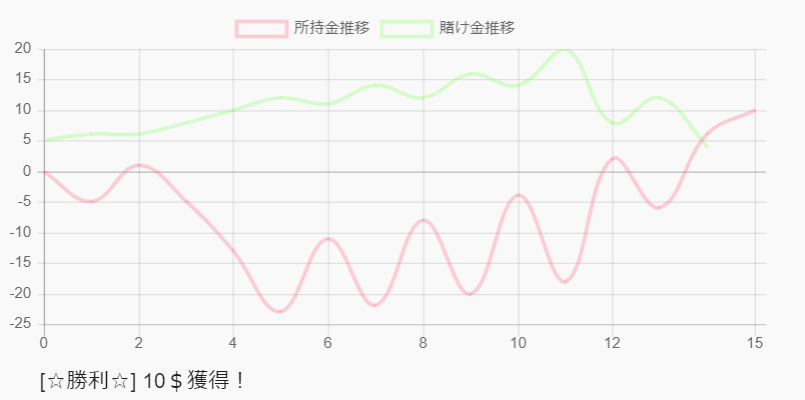
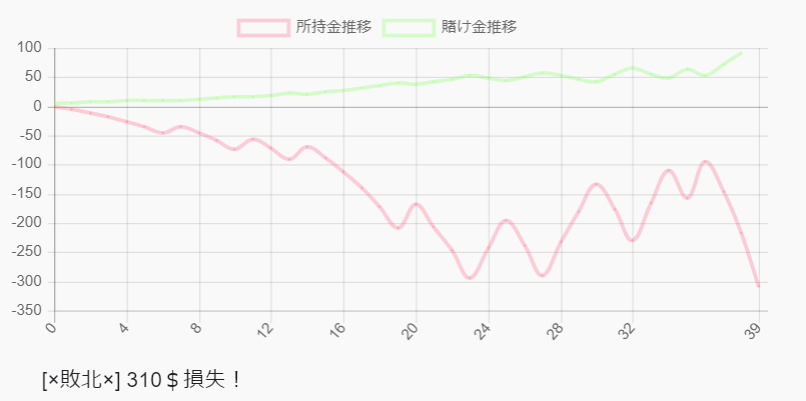
では、「敗北」パターンはどんな感じになるかというと・・・
賭け金の上限値として、100$まで、という低めの天井を設定しているため、
それを超えてしまう場合敗北扱い。
上の例では、その時点で清算したとして、310$失ったことになる。
シミュレーション結果②
さて、多くの人が気になるのは、
個々のゲーム(10$儲けるか、大金を失うか)ではなく、
これを繰り返した場合だろう。
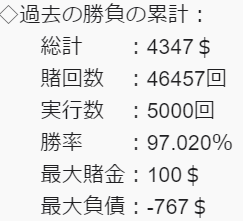
グラフの下の方に、「累計」をテキスト表示している。
PCからアクセスしている場合は、一度実行後、
エンターキーを押下し続けることで、連続して試行できる。
ここから先の結果は、
ぜひご自身のPCのエンターキーの上に
何か文鎮でも置いて試してみて欲しい。
↓↓↓
このページ の「必勝法を試す」から。
↑↑↑
というか、結果がランダムウォーク的性質を持つため、
人によって累計の結果が結構変わってしまう。
総計で、損をする場合もあれば、得をする場合もある。
勝率は、およそ97%ほどになると思われる。
結果考察とまとめ
50%で勝つ勝負ならば、
平均すれば、必ず数字の個数を減らしていくことができる。
このため、賭けの上限などの現実的な制限が無ければ必勝だ!
と、説明することができるため、
誰かに教えると大変自慢できるかもしれない。
(※くどいですが、自己責任でご利用ください)
実際に、本稿で作成したシミュレータでは、
(100$という低めの上限を設定した場合でも)
97%の確率で10$得ることができた。
**数学的に、本当はいくらの期待値なのか?**は、
ここには解を記さない。それがロマン。
だって、クソアプリカレンダーに投稿したから実用度は無い!
(コメント欄で数学的解説をしてくださる方がいたら、
それはそれで大歓迎。)
興味がわいた方は考えてみると面白いかもしれない。
「一回勝負」なら、かなり高確率で少額を稼ぐことができるため、
実戦でも、使い方によっては楽しいと思う。
また、本アプリは、chart.jsで 何かグラフを作るサンプルとして、
目的が欲しくて作ったため、他のグラフサンプルも掲載している。
2%で当たるガチャを、100回引いた時に、一個も出てこない確率は?
ということを計算&グラフ表示できる機能もオススメ。
↓↓↓
このページ の「ガチャる」から。
↑↑↑
そして、chart.jsの練習成果は、
Qiitaの殿堂 の、
分析グラフ編(Qiitaの可視化から見えた、人気技術ランキングの推移)
で活用している。
最後に、主要部分のコードを掲載する。
主要部分のコード掲載
当初はスマホアプリ化することも視野に入れて、
monaca + onsenui で作っていた。
訓練不要で誰でも速読!日本一の速読アプリ「瞬間速読」の個人開発物語(25万DL)
↑の記事で言及している方法と全く同様の方法だ。
スマホアプリにしなくても、そのままWebサイト上でも公開できる。
monaca + onsenui + chart.js まで組み合わせて使うことが可能。
以下主要部分のコード:
function doCalcAndGraph_MON(){
maxkaisuu=parseInt(document.forms.inputform.sikoukaisuu_MON.value,10);
maxbet=parseInt(document.forms.inputform.maxbet_MON.value,10);
//TODO:
//本当は入力チェックする
//データ配列を用意する。
var label_array = [];
var data_array = [];//持ち点の推移
var kakekin_array = [];//賭け金の推移
//モンテカルロ用の配列
var mon_array=[1,2,3,4];
var motiten=0;
//勝負の状況を記録したテキスト
var jyoukyoutext="";
jyoukyoutext+=" ["+mon_array+"]<br>\n";
//一回目は手動で0点を入れる。
label_array.push(0);
data_array.push(motiten);
console.log(mon_array);
//賭けた回数は別途カウントしておく。
var kakekaisuu=0;
for(aa=0 ; aa<maxkaisuu+1 ; aa++){
//現在の長さを確認する。
var length=mon_array.length;
if(length<1){
jyoukyoutext+=" ◆終了◆:◎勝利!<br>\n";
console.log("勝利!");
break;
}
if(length==1){
jyoukyoutext+=" @1で分割<br>\n";
console.log("特殊分割");
//特殊処理:一個だけ数字が残っている場合は、「5」⇒「2」「3」など分割。
//現在1数字しかない。その数字から1を引く。
var lastValue=mon_array[0];
var newValue=Math.floor(lastValue/2);//÷2切り捨て
mon_array=[newValue,lastValue-newValue];
jyoukyoutext+=" ["+mon_array+"]<br>\n";
console.log(mon_array);
}
//特殊分割を行うと配列の長さも変わっているので注意。
//今回賭ける値を設定する。
var betValue= mon_array[0] + mon_array[mon_array.length - 1];
console.log("賭け金:"+betValue);
if(betValue>maxbet){
jyoukyoutext+=" ◆終了◆:×敗北!<br>\n";
console.log("敗北");
break;
}
jyoukyoutext+=" "+betValue+"$賭け ⇒ ";
if( Math.random()<0.5 ){
jyoukyoutext+="◎勝利!<br>\n";
//勝った場合は、先頭と末尾を削除する。
motiten+=betValue;
//先頭要素の削除
mon_array.shift();
//末尾の要素の削除
mon_array.pop();
}else{
jyoukyoutext+="×敗北<br>\n";
//負けた場合は賭けた額に等しい値を末尾に追加する。
motiten-=betValue;
mon_array.push(betValue);
}
jyoukyoutext+=" ["+mon_array+"]<br>\n";
//いくらかけたかのデータを格納する(一個前の配列になる)
kakekin_array.push(betValue);
kakekaisuu+=1;
//記録更新:
if(mon_saidaikakekin<betValue){
mon_saidaikakekin=betValue;
}
if(mon_saidaihusai>motiten){
mon_saidaihusai=motiten;
}
//データを配列に格納する。
data_array.push(motiten);
label_array.push(aa+1);
console.log(mon_array);
}
//合計値の変更
mon_sum_motiten+=motiten;
mon_sum_kaisuu+=kakekaisuu;
mon_sum_monkaisuu+=1;
//描画用のデータにして、実際に描画する。
makeChart_MON( makeChartData_MON(label_array, data_array, kakekin_array));
return 0;
}
function makeChartData_MON(label_array, data_array1, data_array2){
var barChartData = {
labels: label_array,
datasets: [
{
type: 'line', // 追加
label: '所持金推移',
//結合点のサイズ
pointRadius: 0.5,
//結合点のサイズ(ホバーしたとき)
pointHoverRadius: 1,
data: data_array1,
//borderColor : "rgba(254,97,132,0.8)",
//backgroundColor : "rgba(254,97,132,0.5)",
borderColor : "rgba(254,97,132,0.3)",
backgroundColor : "rgba(254,97,132,0)",
yAxisID: "y-axis-RW", // 追加
},
{
type: 'line', // 追加
label: '賭け金推移',
//結合点のサイズ
pointRadius: 0.5,
//結合点のサイズ(ホバーしたとき)
pointHoverRadius: 1,
data: data_array2,
//borderColor : "rgba(254,97,132,0.8)",
//backgroundColor : "rgba(254,97,132,0.5)",
borderColor : "rgba(132,254,97,0.3)",
backgroundColor : "rgba(132,254,97,0)",
yAxisID: "y-axis-RW", // 追加
},
],
};
return barChartData;
}
function makeChart_MON(barChartData){
ctx01 = document.getElementById("canvas_MON").getContext("2d");
//chart.jsは同じキャンバス中にグラフを重ねていくため
//前のグラフがある場合は廃棄を行う。
if(GlfObj_MON){
GlfObj_MON.destroy();
}
GlfObj_MON = new Chart(ctx01, {
type: 'line',
data: barChartData,
options: complexChartOption_MON
});
}
「遊び」の重要性
個人的には、役立たなくても「クソアプリ」という表現は好きではない。
しかし、その観点はとても重要だと思う。
クソアプリ、とは、いわば「遊び」。
実用性が無く役立たなくても、見た人に強烈な印象を残し、
なんらかのインスピレーションを与える場合も多いだろう。
人類の進化は「遊び」からはじまる。
こんな「遊び」が出来るならば、というアイデアに触発される人がでて、
生活にも役に立つような「発明」が生まれるのだ。
~ Char Fuitter (1847~1912 オランダ) ~
この物語はフィクションです。
登場する人物・団体・名称等は架空であり、
実在のものとは関係ありません。
Char Fuitter (チャー・フイター)は架空の人物です。