p5.js で randomGaussian() を使って偏りのある乱数を得る

はじめに

今回の内容は、p5.js の randomGaussian() に関する話です。

●reference | randomGaussian()
　https://p5js.org/reference/#/p5/randomGaussian

randomGaussian() を使った描画を試してみた

今回扱う randomGaussian() を、とりあえず描画に使ってみました。
いくつか試してみたのですが、その中で以下の内容を例に説明などを書いていきます。

それでは、randomGaussian()自体の話、それを使った描画を試した話や、関連情報のメモ的な内容を書いていきます。

p5.js の randomGaussian() について

p5.js の randomGaussian() は、いわゆる「正規分布」「ガウス分布」にしたがって乱数を得る関数です。以下が、randomGaussian() の公式リファレンスのページです。

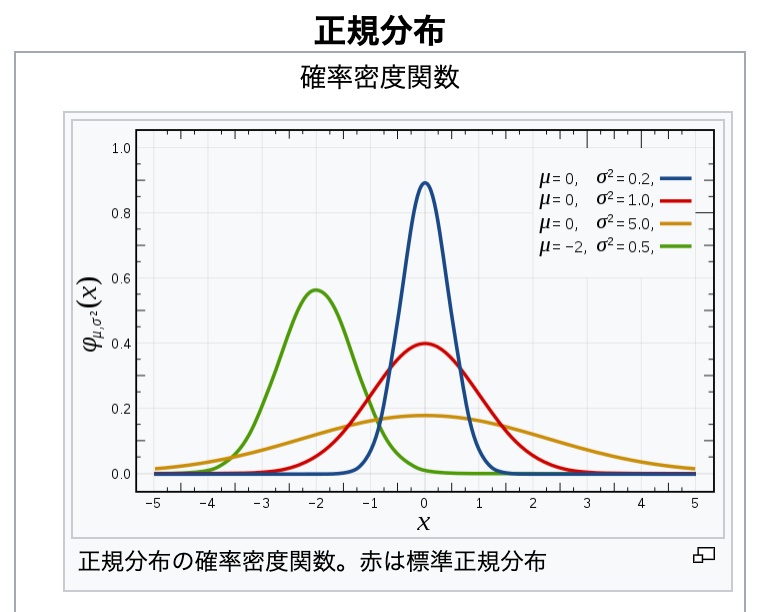
「正規分布（ガウス分布）」は、統計関連の話などで、以下の画像（※ Wikipedia の画像）のような上に出っぱったグラフの形とともに、見かけたことがあるかもしれません。

randomGaussian() で得られる値

p5.js の randomGaussian() は、おおざっぱな書き方をすると、上記の正規分布のグラフの横軸の値をランダムに得る処理で、なおかつ、そのランダムな値の出力には偏りがあり、グラフの高さ方向の値が大きいところの値がより出力されやすい、というものです（なんだか、説明をうまく書けてない気がする...）。

上に示されたグラフの青いグラフで説明すると、横軸のゼロの部分の値・そのすぐ近くの値が大きい（※ グラフの頂点や頂点付近になっている）ため、乱数でゼロやそれに近い値が得られる割合が高いです。
またグラフの形状に関し、ゼロからその両側の（おおよそ）-1・1 の部分に向かって値が大きく減少します。そのため、-1・1 のそれぞれに近い値よりも、ゼロやその付近に近いほうの値が得られやすいです。

おおよそ -1・1 のあたりよりも外側の値に関しては、グラフの値がゼロに近い値になります。そのため、このあたりの範囲の数字が得られることは、割合的に低いです（ただし、全く得られない訳ではないため、上記の公式リファレンスで「There's no minimum or maximum value」というように「得られる値の範囲の最小値・最大値はない」という書き方がされています）。

randomGaussian() で指定できる引数

randomGaussian() の引数指定は、「なし」「数値 1つ」「数値 2つ」の 3パターンがあります（※ 公式リファレンスでの説明は、以下の部分）。

3つそれぞれの場合にどうなるかを補足すると、乱数を得る際に用いられる正規分布が以下のようになります。

• 引数の指定
  • なし： 平均（mean）がゼロ、標準偏差（sd）が 1 の正規分布（標準正規分布、または基準正規分布）となる
  • 数値 1つ： 指定した数値が正規分布の平均に用いられる（標準偏差はデフォルトの 1 になる）
  • 数値 2つ： 指定した1つ目の数値が正規分布の平均に、2つ目の数値が正規分布の標準偏差に用いられる

このようにして引数を指定することで、乱数を得る際の正規分布に関して、「中央の位置にあたる部分 ＝ 平均（mean）」や「横方向の拡がりに関わる部分 ＝ 標準偏差（sd）」を、デフォルトの値から変更できます。

randomGaussian() を使った描画

ここで、冒頭で示していた、randomGaussian() を使った描画に関して、実装した内容を以下に掲載します。

function setup() {
  createCanvas(500, 400);

  frameRate(0.5);

  noStroke();
  fill(230, 255 * 0.5);

  drawGaussianCircles();
}

function draw() {
  drawGaussianCircles();
}

function drawGaussianCircles() {
  background(40);

  for (let i = 0; i < 30; i++) {
    const centerX = randomGaussian(width * 0.5, width * 0.2);
    const centerY = randomGaussian(height * 0.5, height * 0.2);
    circle(centerX, centerY, (i + 10) * 2);
  }
}

上記のプログラムは、 frameRate(0.5) としているので、2秒に 1回のペースで drawGaussianCircles() の部分の描画を行います。

drawGaussianCircles() は、30個の円を描画する処理です。
その円の描画で、x座標・y座標を決める部分に randomGaussian() を使っています。

randomGaussian() を使っている部分の補足

randomGaussian() を使って x座標・y座標を決めている部分は以下です。

    const centerX = randomGaussian(width * 0.5, width * 0.2);
    const centerY = randomGaussian(height * 0.5, height * 0.2);
    circle(centerX, centerY, (i + 10) * 2);

ここでは、キャンバスの幅、または高さの値を元に、正規分布の平均と標準偏差を決めています。

平均の値は、キャンバスの幅、または高さの半分の値にしているため、ランダムに得られる座標は、画面中央やその付近になる確率が高く、そこから離れた位置の座標ほど、出力されにくくなります。

また、標準偏差の値はキャンバスの幅、または高さに 0.2 を乗算した値にしています。
これにより、極端に画面中央の座標が出やすくなるのではなく、その周辺の位置の座標もある程度は出力されるようになっています。

円の大きさの変更

randomGaussian() とは関係ない話になりますが、見た目に不均一さを出すため、円の大きさを (i + 10) * 2 という値にしています。これにより、30個の円の大きさがそれぞれ異なります。

randomGaussian() の標準偏差の値を変えた場合の出力の違い

上記で、randomGaussian() の引数に 0．2 という係数を用いて指定していた標準偏差に着目してみます。その標準偏差の値を変えた場合の出力がどう異なるか、少しここで掲載してみます。

基本的に標準偏差の値が小さくなると、平均の値（上の例だと、キャンバスの横・縦方向の中央部分）に近い部分が出力されやすくなり、逆に標準偏差の値を大きくすると、平均の値から離れた値も出力されやすくなります。

以下に、標準偏差の値を上記の半分にした場合と、2倍にした場合の一例をそれぞれ示します。
標準偏差の値が小さいと、中心に近い部分に円が多く出力され、逆に標準偏差の値が大きいと、出力される円が広く分布している様子が確認できます。

標準偏差の値が上記の半分

標準偏差の値が上記の 2倍

おわりに

今回、p5.js の randomGaussian() を使った描画を試してみました。

randomGaussian() を使ってみたのは今回が初めてだったのですが、他に何か面白い使い方ができないか模索してみようと思います。

【余談】 random() で偏りのある乱数を得る

今回用いた randomGaussian() ではなく random() で偏りのある乱数を得る方法もあります。

それについて、以下のサイトに分かりやすく事例付で書かれているので、興味がある方はご参照くださ

●JavaScript開発に役立つ重要なランダムの数式まとめ - ICS MEDIA
　https://ics.media/entry/11292/

【追記】 randomGaussian() をテクスチャの描画に活用する

randomGaussian() を、以下のようなテクスチャの描画に使ってみました。

これをやってみたきっかけになったネタ元動画があるので、以下で紹介します。

https://youtu.be/lNxMKPGSpBQ?si=nKy9PUArxenr3_ff&t=825