はじめに
前回の記事では、回帰分析の1つである単回帰分析について書きました。
この記事では、変数同士の相関関係から変動を予測することができる重回帰分析について書きます。
重回帰分析はどのような時に使われるのか。
重回帰分析は、マーケティングで使われる分析手法のひとつです。複数の変数を持つデータの関連性を明らかにします。
例えば、店舗面積/従業員数/商圏人口/広告費から、来客数を予測したり、
他にも、部屋の広さ/駅からの距離/犯罪発生率から、家賃を予測します。
このように、複数の要因から1つの値を予測するときに、重回帰分析を利用します。
また、重回帰分析では、それぞれの要因が予測したい値に与える影響度合を数値で表現できます
そのため、要因分析としても使われます。店舗面積/従業員数/商圏人口/広告費それぞれが、来店客数を増やす要因なのか、減らす要因なのかが分かります。
要因分析をすることで、来店客数を増やす有効なパラメータを定量的に評価することができ、マーケティングでも使われています。
重回帰分析は、様々な分野において、変動する値を予測するためや、要因分析のために使われています。
この記事では、重回帰分析の原理原則を理解することを目的とし、どのようなアルゴリズムで回帰係数を算出しているのかを紐解きます。
まずは、回帰分析の説明をします。
回帰分析とは
回帰分析とは、結果となる数値と要因となる数値の関係を数式(回帰式)で表す統計的手法です。
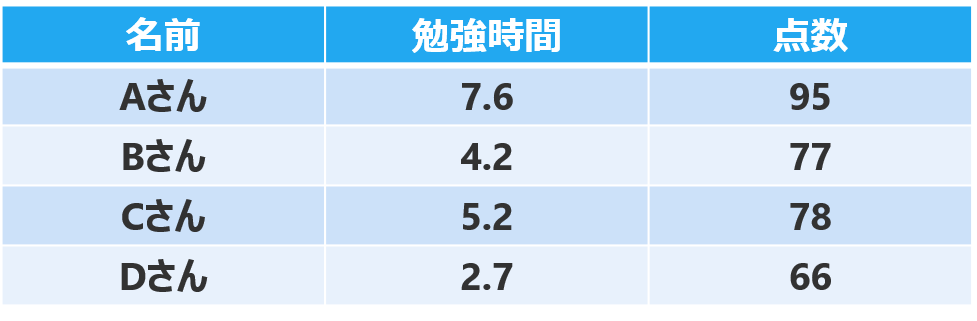
例えば、あるクラスのAさん〜Dさんの「勉強時間」と「テストの点数」のデータがあります。
このデータを視覚化すると、下のようなグラフになります。
横軸が勉強時間、縦軸がテストの点数を表しています。
勉強時間が長くなるほど、テストの点数が上がっている傾向がわかります。
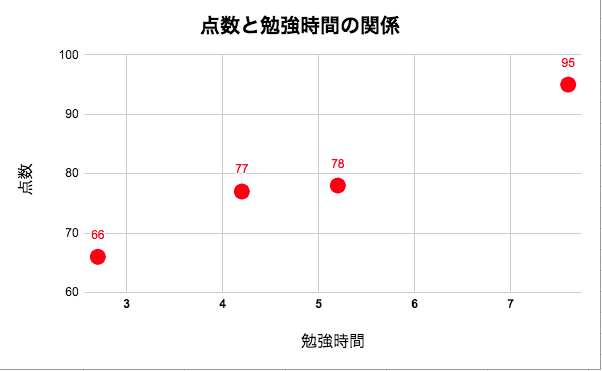
4人のデータを用いて、「勉強時間」と「テストの点数」の関係を数式で表します。
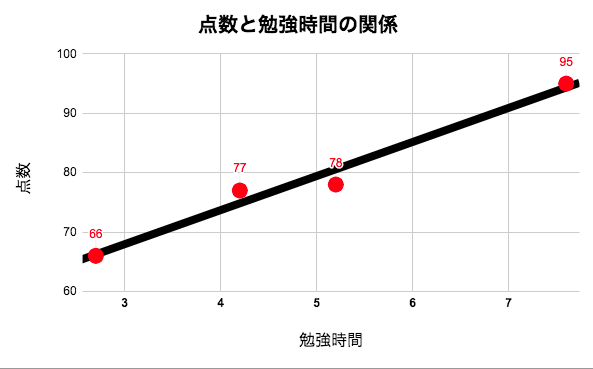
「勉強時間」と「テストの点数」の関係が線形であると仮定して、データに当てはまる直線を下記のように引きます。
黒の直線は下の式(回帰式)で表せます。
y = 5.7x + 51
この式(回帰式)の意味は、
(点数)= 5.7 × (学習時間) + 51
となります。
学習時間が0のとき、51点となり、1時間勉強するごとに5.7点ずつ点数が上がっていることを意味しています。
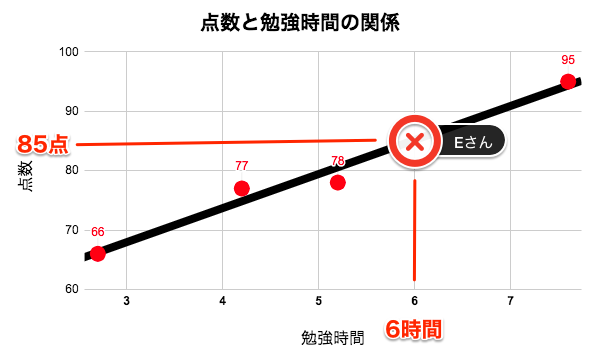
この式(回帰式)を利用することで、勉強時間から、他の生徒がどの程度の点数を獲得できるかが予測できるようになります。
例えば、勉強時間が6時間のEさんの点数は、
\begin{align}
(Eさんの点数) &= 5.7× (学習時間) + 51 \\
&= 5.7 × 6 + 51 \\
&= 85(点)
\end{align}
と求めることができます。
このように、回帰分析は、結果となる数値と要因となる数値の関係を回帰式で表します。
また、要因となる数値を説明変数、結果となる数値を目的変数といいます。
今回の例でいうと、「勉強時間」から「点数」を予測したので、「勉強時間」が説明変数で、「点数」が目的変数となります。
回帰分析のうち、1つの目的変数を1つの説明変数で予測するものを単回帰分析と言います。
そして、1つの目的変数を2つ以上の説明変数で予測するものを重回帰分析と言います。
単回帰分析
y = a + b_1x_1 \\
重回帰分析
y = a + b_1x_1 + b_2x_2 + ・・・ + b_nx_n \\
y:目的変数 \\
a:切片 \\
b:回帰係数 \\
x:説明変数
では、どのようにしてインプットしたデータから、回帰式を算出しているのか。
それは、回帰式をコスト関数で算出したコストで評価し、最急降下法で、コストが小さい回帰係数を算出します。
コスト関数や、最急降下法を初めて聞く方は、前回の記事を一読した方がわかりやすいかもしれません。(参考:単回帰分析の原理原則)
本記事では、重回帰分析におけるコスト関数と最急降下法について述べていきます。
それでは、物理の点数、科学の点数のデータから数学の点数を予測するモデルケースを通して、重回帰分析を実装していきます。
データの確認
CSVファイルを読み込み、データを確認します。
今回使用する学習データはこちらをクリック
| Pysics | Science | Statistics | Math |
|---|---|---|---|
| 64 | 67 | 69 | 68 |
| 74 | 74 | 63 | 67 |
| 60 | 59 | 55 | 57 |
| 84 | 88 | 89 | 91 |
| 80 | 88 | 78 | 82 |
| 75 | 68 | 68 | 63 |
| 66 | 59 | 55 | 65 |
| 77 | 71 | 66 | 73 |
| 70 | 71 | 60 | 67 |
| 89 | 84 | 80 | 85 |
| 73 | 76 | 69 | 82 |
| 78 | 74 | 63 | 67 |
| 67 | 63 | 67 | 57 |
| 80 | 81 | 83 | 74 |
| 72 | 75 | 73 | 83 |
| 68 | 63 | 76 | 71 |
| 81 | 89 | 80 | 85 |
| 64 | 66 | 59 | 69 |
| 79 | 81 | 79 | 87 |
| 70 | 76 | 69 | 71 |
| 76 | 80 | 68 | 80 |
| 71 | 64 | 75 | 66 |
| 81 | 77 | 84 | 73 |
| 85 | 83 | 87 | 90 |
| 61 | 67 | 70 | 61 |
| 74 | 71 | 75 | 73 |
| 85 | 82 | 78 | 84 |
| 60 | 60 | 57 | 52 |
| 83 | 88 | 80 | 92 |
| 85 | 80 | 76 | 87 |
| 84 | 86 | 86 | 80 |
| 82 | 79 | 88 | 83 |
| 68 | 66 | 60 | 71 |
| 89 | 85 | 88 | 91 |
| 85 | 90 | 85 | 98 |
| 68 | 66 | 62 | 61 |
| 74 | 76 | 82 | 77 |
| 76 | 75 | 84 | 81 |
| 62 | 68 | 70 | 60 |
| 64 | 67 | 68 | 73 |
| 65 | 66 | 59 | 58 |
| 64 | 57 | 56 | 57 |
| 73 | 74 | 63 | 69 |
| 65 | 65 | 69 | 69 |
| 87 | 91 | 97 | 97 |
| 62 | 60 | 61 | 57 |
| 77 | 69 | 62 | 70 |
| 77 | 76 | 75 | 70 |
| 89 | 97 | 94 | 99 |
| 63 | 56 | 59 | 62 |
| 74 | 69 | 62 | 75 |
| 72 | 67 | 67 | 67 |
| 69 | 77 | 81 | 73 |
| 88 | 86 | 95 | 86 |
| 77 | 84 | 75 | 87 |
| 83 | 80 | 77 | 80 |
| 77 | 77 | 80 | 74 |
| 84 | 83 | 86 | 87 |
| 77 | 79 | 69 | 83 |
| 66 | 74 | 71 | 74 |
| 74 | 69 | 79 | 75 |
| 67 | 75 | 78 | 73 |
| 83 | 85 | 85 | 93 |
| 72 | 65 | 73 | 69 |
| 70 | 76 | 73 | 83 |
| 71 | 70 | 74 | 75 |
| 89 | 94 | 82 | 86 |
| 82 | 86 | 85 | 89 |
| 86 | 80 | 88 | 75 |
| 85 | 89 | 100 | 97 |
| 89 | 83 | 79 | 76 |
| 77 | 74 | 74 | 71 |
| 79 | 83 | 93 | 89 |
| 75 | 71 | 79 | 78 |
| 68 | 66 | 68 | 67 |
| 64 | 56 | 57 | 58 |
| 66 | 60 | 55 | 57 |
| 81 | 76 | 80 | 80 |
| 68 | 72 | 71 | 79 |
| 71 | 70 | 75 | 72 |
| 62 | 54 | 56 | 54 |
| 80 | 85 | 93 | 85 |
| 80 | 84 | 86 | 83 |
| 66 | 62 | 67 | 58 |
| 73 | 77 | 69 | 74 |
| 70 | 70 | 71 | 67 |
| 62 | 55 | 62 | 56 |
| 62 | 70 | 76 | 76 |
| 74 | 67 | 65 | 65 |
| 80 | 83 | 78 | 78 |
| 90 | 84 | 83 | 90 |
| 84 | 76 | 78 | 70 |
| 84 | 87 | 96 | 92 |
| 78 | 81 | 80 | 78 |
| 90 | 92 | 81 | 89 |
| 60 | 68 | 55 | 65 |
| 86 | 85 | 80 | 93 |
| 72 | 64 | 59 | 69 |
| 69 | 63 | 62 | 57 |
import numpy as np
import pandas as pd
data = np.loadtxt('./training_data_multipleLiner.csv',delimiter=",",skiprows =1)
df = pd.DataFrame(data,columns=['物理','科学','統計','数学'])
| 物理 | 科学 | 統計 | 数学 | |
|---|---|---|---|---|
| 0 | 64.0 | 67.0 | 69.0 | 68.0 |
| 1 | 74.0 | 74.0 | 63.0 | 67.0 |
| 2 | 60.0 | 59.0 | 55.0 | 57.0 |
| • | • | • | • | • |
| 98 | 69.0 | 63.0 | 62.0 | 57.0 |
こちらのデータセットには、99人分の物理、科学、統計、数学のテストの点数の情報が入っています。
今回は、物理の点数と科学の点数から、数学の点数と予測する重回帰分析をしていきます。
つまり、説明変数が物理の点数と科学の点数として、目的変数を数学の点数とします。
初めに、説明変数と目的変数の関係を視覚化します。
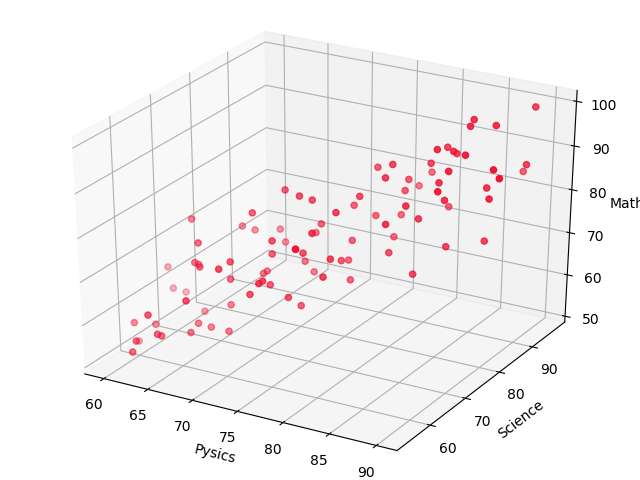
x軸を物理の点数、y軸を科学の点数、z軸を数学の点数でデータをプロットします。
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 点数をプロットしてみる
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(df['物理'],df['科学'],df['数学'],color='#ef1234')
ax.set_xlabel('Pysics')
ax.set_ylabel('Science')
ax.set_zlabel('Math')
plt.show()
なんとなく、科学が高い人が数学も高そうな感じがしますが、正直よくわかりませんね。
このグラフからは、数学の点数を予測するのに、物理と科学、どちらの点数が重要なのか、どのくらい関係があるのかまではわかりません。
そこで重回帰分析により、下記の式の回帰係数と切片を算出し、物理の点数と科学の点数が、数学の点数に与える影響度合いを分析していきます。
(数学の点数) = 切片 + b_1×(物理の点数) + b_2(科学の点数) \\
b:回帰係数 \\
データの前処理
元のデータをそのまま利用して、学習することも可能です。
(ここで言う学習は、データから回帰係数と切片を算出することを指しています。)
一般的に、各特徴量間でデータのスケールが異なる場合、事前にデータのスケールを調整したほうが、パラメータに偏りがなくなるので、より効率的に学習が行えるようになります。
今回の例で言うと、テストの点数なので最低点は0点、最高100点ですが、それぞれの教科の難易度により平均点や分散などが変わってきます。
そこでデータのスケールを合わせるだけでなく、各特徴量を標準正規分布に従うように変換する標準化を行います。
機械学習の手法は「入力のそれぞれの特徴量がどう変化したら、出力がどう変化するのか」を見ているので、各特徴量のばらつき度合い(標準偏差)を揃えておくことで、各特徴量の動きに対する感度を平等に見ることができるようになるわけです。
データの標準化を行う。
標準化は下記に式で行います。
具体的には、各特徴量で、平均を0、標準偏差を1になるように調整します。
x = \frac{x - x_{mean}}{x_{std}} \\
x_{mean}:xの平均値 \\
x_{std}:xの標準偏差 \\
# 正規化(Z-score Normalization)
def norm(X):
X_norm = np.zeros((X.shape[0],X.shape[1]))
mean = np.zeros((1,X.shape[1]))
std = np.zeros((1,X.shape[1]))
for i in range(X.shape[1]):
mean[:,i] = np.mean(X[:,i])
std[:,i] = np.std(X[:,i])
X_norm[:,i] = (X[:,i] - float(mean[:,i])) / float(std[:,i])
return X_norm,mean,std
標準化を行う関数を定義したので、データの標準化を行います。
また、標準化ができているのか、平均と標準偏差を確認して見ましょう。
# 説明変数はX、目的変数はy
X=data[:,:2]
y=data[:,3]
# 標準化
X_norm,mean,std = norm(X)
# 標準化の確認
print("Xの平均値 = {}".format(X_norm.mean()))
print("Xの標準偏差 = {}".format(X_norm.std()))
ちゃんと標準化できていますね。
# Xの平均値 = 2.0634448134447354e-16
# Xの標準偏差 = 0.9999999999999999
コスト関数
コスト関数(平均二乗誤差)は、ある回帰式が学習データとどれだけフィットしているかを定量的に評価します。
今回は、説明変数は科学の点数と物理の点数の2種類ですので、下記の式のようになります。
y = w_0 + w_1x_1 + w_2x_2 \\
\begin{align}
y&:目的変数 \\
w_0&:切片 \\
w_1,w_2&:回帰係数 \\
x&:説明変数
\end{align}
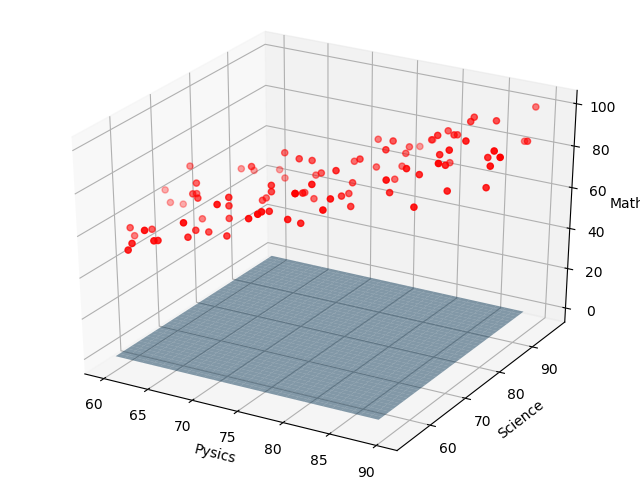
例えば、(w0,w1,w2) = (0,0,0) のときは、下図のような平面になります。
コスト関数を数式で表すと下記の式になります。
\begin{align}
J(w_0,w_1,w_2) &= \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}-y)^2
\end{align}
また、回帰式をベクトルで表すと、
\begin{align}
\hat{y} &= w_0 + w_1x_1 + w_2x_2 \\
&= XW
\end{align}
X=\left[
\begin{matrix} x_0 & x_1 & x_2 \end{matrix}
\right]
,
W=\left[
\begin{matrix} w_0 \\ w_1 \\ w_2 \end{matrix}
\right]
(x_0 = 1)
と表せます。
数式で見ると難しそうに見えますが、やっていることは単純です。
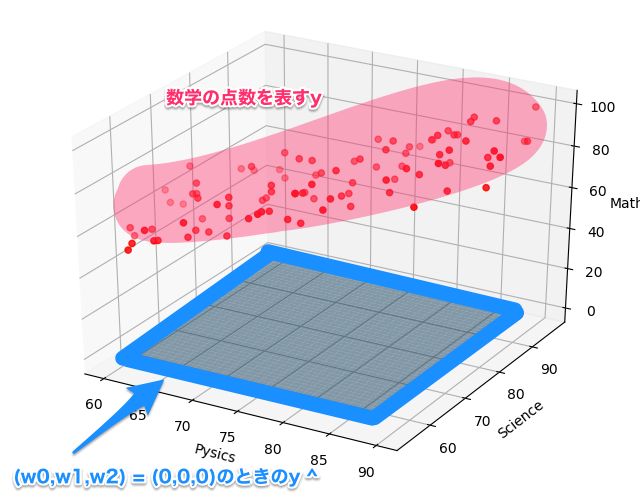
まず、yは、学習データの目的変数(数学の点数)です。下の図で言うと、赤点のことです。
次に、y^は、学習データの説明変数(物理・科学の点数)に回帰係数をかけた予測値です。下の図で言うと、青い平面です。
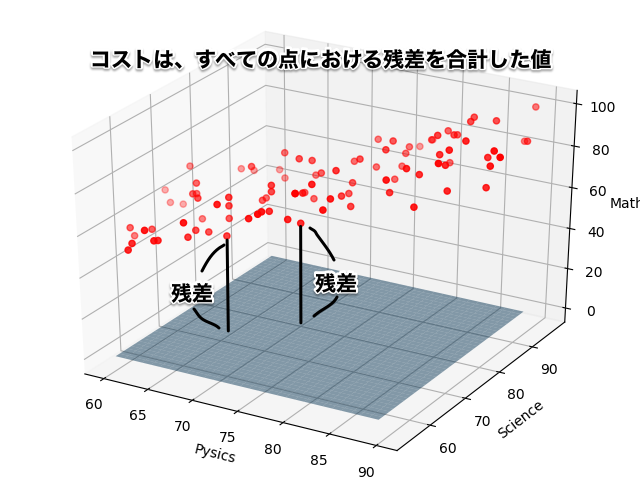
コスト関数は、それぞれの点における予測値と、実際の答えの差(残差)を計算し、全ての残差を合計した値となります。(正確には、個数の2倍で割っています。)
ちなみに上図のコストを計算すると、2882となります。
次に、(w0,w1,w2) = (50,3,3) のときを考察して見ます。
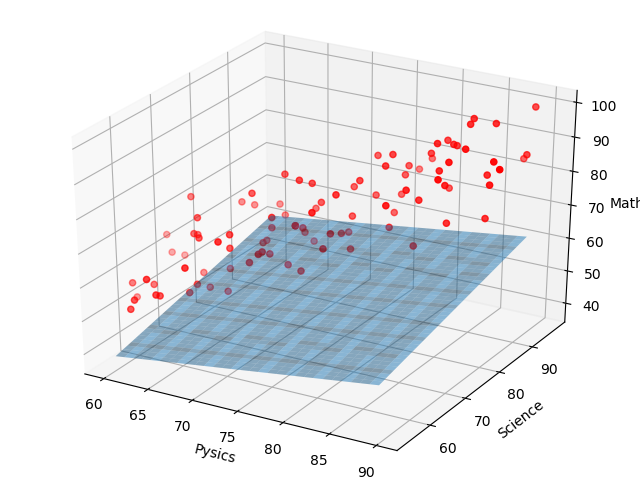
先ほどよりは、若干データに近づいていることがわかります。
この時のコストを計算すると、552となります。
先ほどが2882だったのに対して、552と、コストが大幅に減ったことがわかります。
このように、コスト関数を用いることで、ある回帰式が学習データとどれだけフィットしているかを定量的に評価することができます。
それでは実装していきます。
まずは、切片の計算を工夫するために、先ほど標準化した説明変数に切片項(x0)を追加します。
切片項(x0)は1です。
また、(w0,w1,w2)の初期値を(0,0,0)と定義します。
# 切片項を追加
X_padded = np.column_stack((np.ones((len(y),1)),X_norm))
# モデル式のパラメータ初期化
weight_int = np.zeros((3,1))
次に、コスト関数を定義します。
# コスト関数
def cost(X,y,weight):
m = len(y)
J = 0
y_hut = X.dot(weight)
diff = np.power((y_hut - np.transpose([y])),2)
J = (1.0 /(2*m)) * diff.sum(axis = 0)
return J
これでコスト関数を定義できました。
例えば先ほど(w0,w1,w2) = (50,3,3)のときのコストは、下記のように求められます。
# コスト関数
print(cost(X_padded,y,[50,3,3])[0])
# 552
これで、ある回帰式が、学習データにどれほどフィットしているかを定量的に評価できるようになりました。
あとは、コストが最小となるような回帰係数を、最急降下法で求めていきます。
最急降下法
最急降下法は、関数を最小にするようなパラメーターを求めるためのアルゴリズムです。
今回はコストが最小になる回帰係数(w0,w1,w2)を求めます。
コスト関数は下記の式でした。
\begin{align}
J(w_0,w_1,w_2) &= \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}-y)^2 \\
&= \frac{1}{2m}\sum_{i=1}^{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)^2
\end{align}
\begin{align}
m &: データ数 \\
\hat{y} &: 予測値 (\hat{y}=w_0x_0 + w_1x_1 + w_2x_2) \\
y &: 実測値
\end{align}
コスト関数をw0で偏微分すると、
\begin{align}
\frac{\partial }{\partial w_0}J(w_0,w_1,w_2) &= \frac{\partial }{\partial w_0}\frac{1}{2m}\sum_{i=1}^{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)^2 \\
&= \frac{1}{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)
\end{align}
コスト関数をw1で偏微分すると、
\begin{align}
\frac{\partial }{\partial w_1}J(w_0,w_1,w_2) &= \frac{\partial }{\partial w_1}\frac{1}{2m}\sum_{i=1}^{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)^2 \\
&= \frac{1}{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)x_1
\end{align}
コスト関数をw2で偏微分すると、
\begin{align}
\frac{\partial }{\partial w_1}J(w_0,w_1,w_2) &= \frac{\partial }{\partial w_1}\frac{1}{2m}\sum_{i=1}^{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)^2 \\
&= \frac{1}{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)x_2
\end{align}
と求めることができます。
偏微分をすると、コスト関数の傾きがわかります。
コストが小さくなるように、w0,w1を更新したいので、元々の回帰係数から偏微分で得られた値を引きます。
\begin{align}
w_0 &:= w_0 - \alpha\frac{1}{m}(w_0x_0 + w_1x_1 + w_2x_2 - y) \\
w_1 &:= w_1 - \alpha\frac{1}{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)x_1 \\
w_2 &:= w_1 - \alpha\frac{1}{m}(w_0x_0 + w_1x_1 + w_2x_2 - y)x_2
\end{align}
\begin{align}
\alpha &:学習率 \\
m &:データ数 \\
x &:説明変数 \\
y &:目的変数 \\
\end{align}
αは学習率と呼ばれ、回帰係数を更新する値の大きさを調整します。
学習率は、大きすぎると回帰係数が収束しない可能性があり、また、小さすぎると、回帰係数の収束に時間がかかってしまいます。
今回は学習率=0.01でと決めて、進めていきます。
では、最急降下法を実装していきます。
# 最急降下法
def gradientDescent(X,y,weight,alpha,iterations):
m=len(y)
J_history = np.zeros((iterations,1))
weight_history = []
for i in range(iterations):
weight = weight - alpha * (1.0/m) * np.transpose(X).dot(X.dot(weight) - np.transpose([y]))
weight_history.append(weight)
J_history[i] = cost(X,y,weight)
print(alpha * (1.0/m) * np.transpose(X).dot(X.dot(weight) - np.transpose([y])))
return weight,J_history,weight_history
今回は、500回の回帰係数の更新する中で、コストがどのように推移するかを可視化するために、J_historyを追加しています。
また、更新された回帰係数を保持するために、weight_historyを追加しています。
次にα、学習回数の初期値を設定します。
# 学習率と学習回数(イテレーション)
alpha = 0.01
num_iters = 500
それではコスト関数と最急降下法を用いて、モデルの学習をしていきます。
weight,J_history,weight_history = gradientDescent(X_padded,y,weight_int,alpha,num_iters)
print(weight)
# [[74.57745626]
# [ 3.29981383]
# [ 7.16228608]]
回帰係数を求めることができました。
つまり、数学の点数は下記の式で表すことが出来ます。
(数学の点数)= 3.29×(標準化した物理の点数) + 7.16×(標準化した科学の点数) + 74.5
どちらの回帰係数も正であるので、物理や科学の点数が高い方が数学の点数が高い傾向がわかります。
また、数学の点数には、物理の点数よりも科学の点数の方が、2倍以上関係があることを示しています。
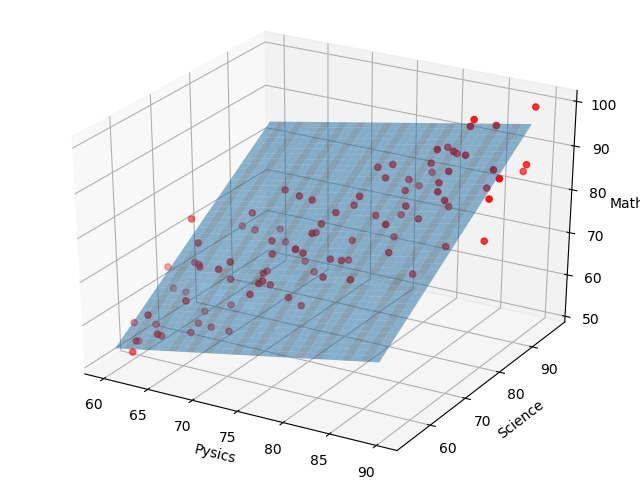
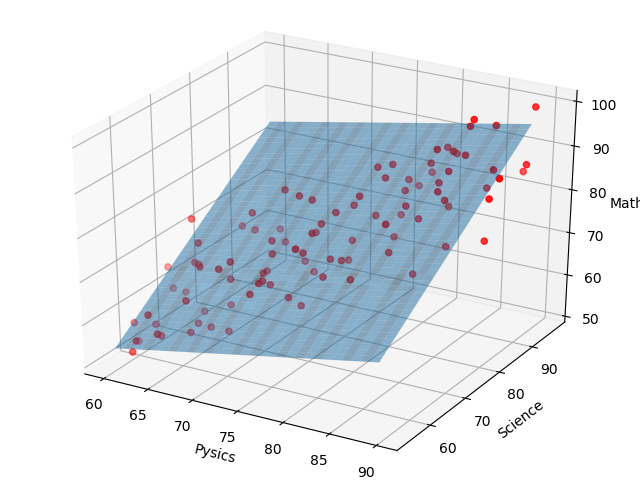
また、回帰式と学習データを視覚化すると、
# 実測値の描画
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(data[:,0],data[:,1],data[:,3],color='red')
# 回帰平面の描画
X,Y = np.meshgrid(np.arange(data[:,0].min(),data[:,0].max(),1),np.arange(data[:,1].min(),data[:,1].max(),1))
X_norm = (X-float(mean[:,0])) / float(std[:,0])
Y_norm = (Y-float(mean[:,1])) / float(std[:,1])
Z = weight[0] + weight[1] * X_norm + weight[2] * Y_norm
ax.plot_surface(X,Y,Z,alpha=0.5)
# ラベルを追加
ax.set_xlabel('Pysics')
ax.set_ylabel('Science')
ax.set_zlabel('Math')
plt.show()
このように、学習データにフィットした平面を描くことができました。
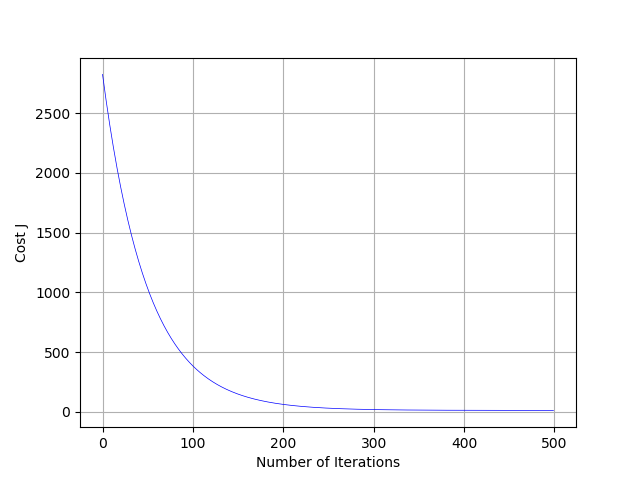
また、コストの推移も確認してみましょう。
# コストと学習回数のグラフ
plt.plot(range(J_history.size),J_history,"-b",linewidth=0.5)
plt.xlabel("Number of Iterations")
plt.ylabel("Cost J")
plt.grid(True)
plt.show()
縦軸がコストで、横軸が学習回数を表しています。
学習を繰り返すごとに、コストが下がっているのがわかります。
学習の推移を確認してみる。
500回、回帰係数を更新しました。その履歴がweight_historyに格納されているので、確認してみます。
nums = [0,99,199,299,399,499]
for num in nums:
weight = weight_history[num]
# 実測値の描画
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(data[:,0],data[:,1],data[:,3],color='red')
# 回帰平面の描画
X,Y = np.meshgrid(np.arange(data[:,0].min(),data[:,0].max(),1),np.arange(data[:,1].min(),data[:,1].max(),1))
X_norm = (X-float(mean[:,0])) / float(std[:,0])
Y_norm = (Y-float(mean[:,1])) / float(std[:,1])
Z = weight[0] + weight[1] * X_norm + weight[2] * Y_norm
ax.plot_surface(X,Y,Z,alpha=0.5)
# ラベルを追加
ax.set_xlabel('Pysics')
ax.set_ylabel('Science')
ax.set_zlabel('Math')
plt.savefig('{}回目.png'.format(num))
学習回数が1回、100回、200回、300回、400回、500回のときを描画します。
学習回数が1回のとき、(w0,w1,w2) = (0.75,0.09,0.10)となり、下記のようになります。
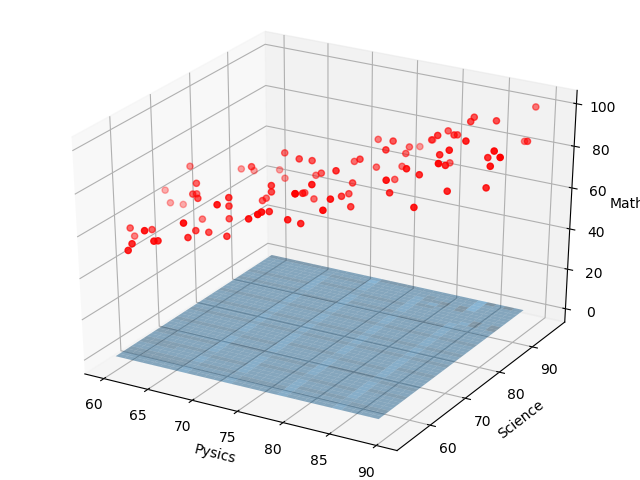
まだ学習を1度しかしていないため、初期の平面から動きがほとんどありませんね。
学習回数が100回のとき、(w0,w1,w2) = (47.5,3.95,4.93)となり、下記のようになります。
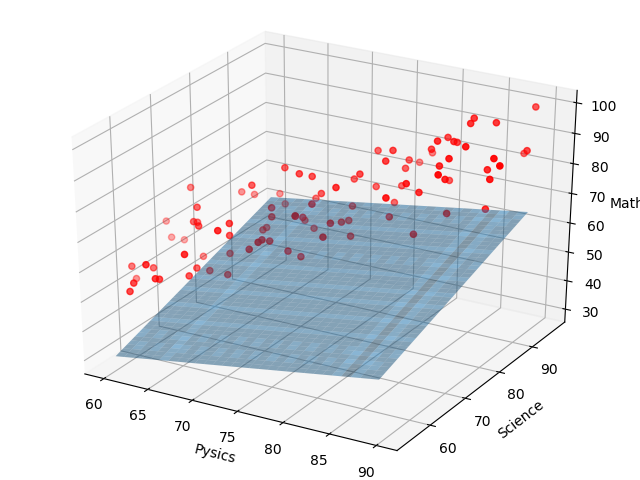
100回の学習で、平面が大きく傾いてきました。
傾きはなんとなく良さそうですが、高さ(切片)が足りてないようです。
学習回数が200回のとき、(w0,w1,w2) = (65.0,4.18,6.03)となり、下記のようになります。
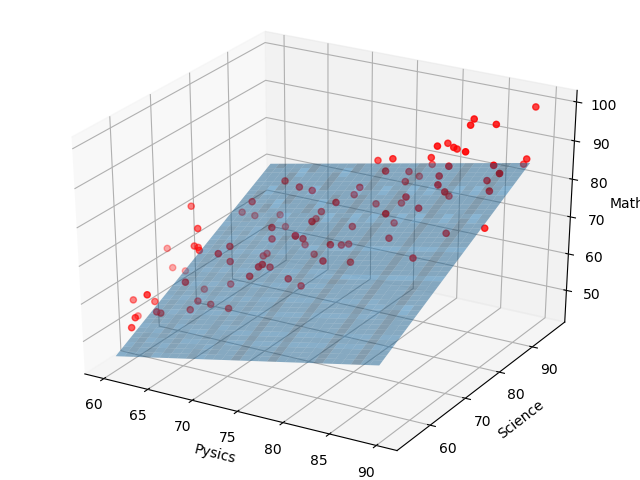
パッとみた感じだと、これで良さそうに見えます。
学習回数が200回のときを見ると、コストは大幅に減少しています。
学習回数が300回のとき、(w0,w1,w2) = (71.3,3.91,6.51)となり、下記のようになります。
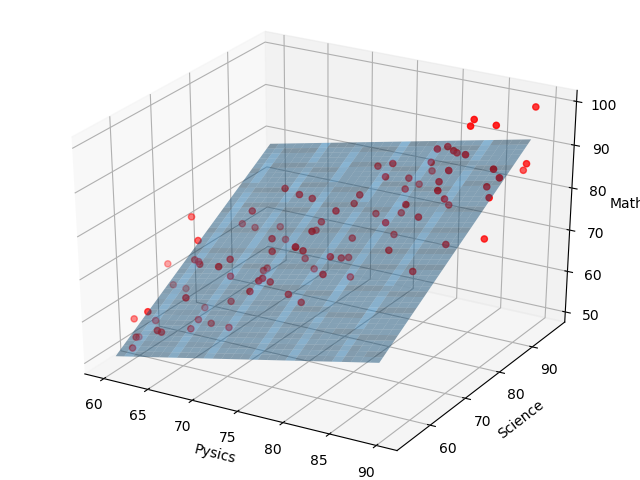
4.18あった物理の回帰係数が、3.91に下がりました。
ここまで上昇傾向にあった係数が下がりました。微調整が行われています。
学習回数が400回のとき、(w0,w1,w2) = (73.7,3.59,6.86)となり、下記のようになります。
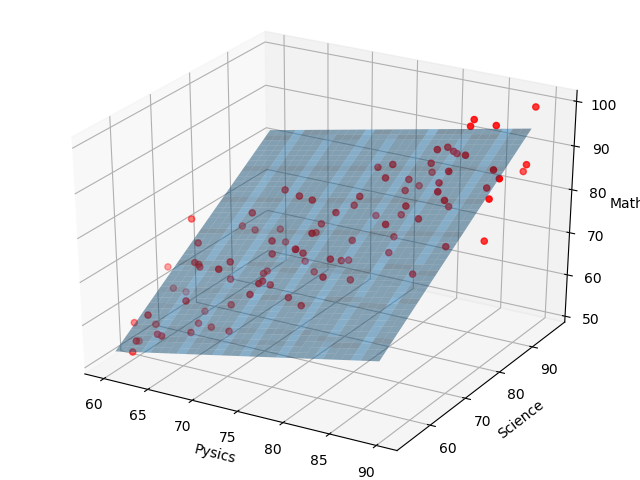
学習回数が500回のとき、(w0,w1,w2) = (74.5,3.29,7.16)となり、最終的に下記の通りに落ち着きます。
まとめ
本記事では、重回帰分析についてまとめました。
重回帰分析の魅力は、関連性がわからないデータから、回帰係数という形で正・負の関連度合を算出できる点だと思います。
次は、重回帰分析を発展させたリッジ回帰やLasso回帰、Elastic Netにも取り組んでみたいと思ってます。