単回帰分析の原理原則

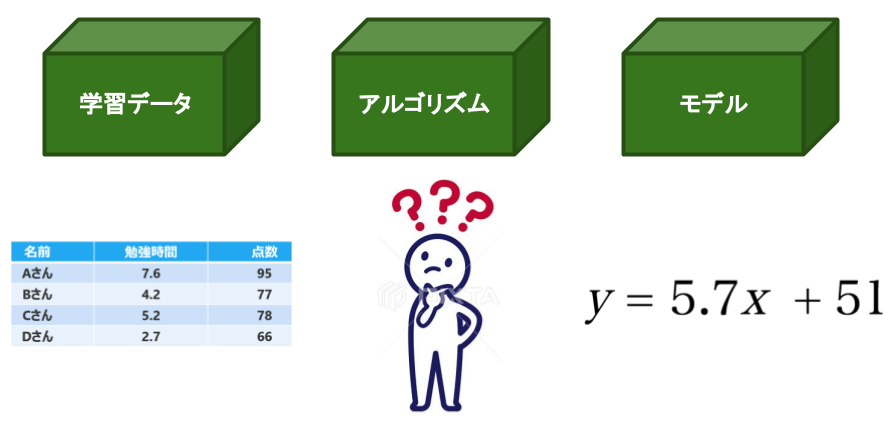
はじめに

フューチャー Advent Calendar 2019（2）の19日目です。
18日目は、noko_qiiさんの「SageMakerとpapermillでサクッと始めるJupyterNotebookベースな機械学習案件向け開発環境構築・利用ガイドライン」でした。
Advent Calendarって、社内の人が様々なトピックで記事を投稿していて面白いですね。

無事に新人研修が終わり、需要予測のチームに配属されました。
今日は、最近学んだことの中から、回帰分析の１つである単回帰分析についてまとめました。

回帰分析って何？

回帰分析とは、結果となる数値と要因となる数値の関係を数式(回帰式)で表す統計的手法です。
具体例を交えながら説明します。
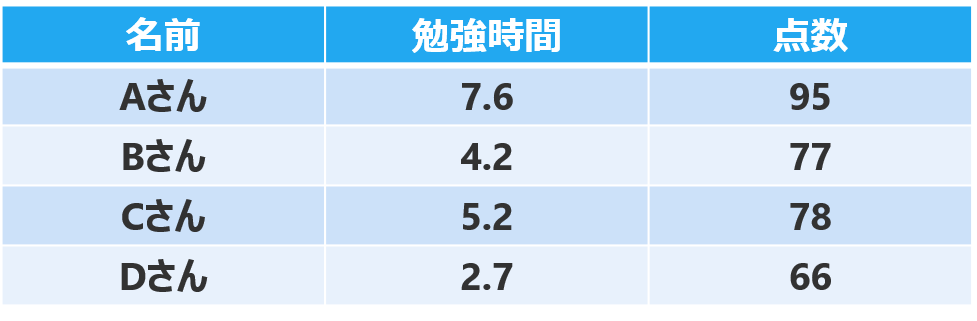
例えば、あるクラスのAさん〜Dさんの「勉強時間」と「テストの点数」のデータがあります。
回帰分析は、「勉強時間」と「テストの点数」の関係を数式で表現します。

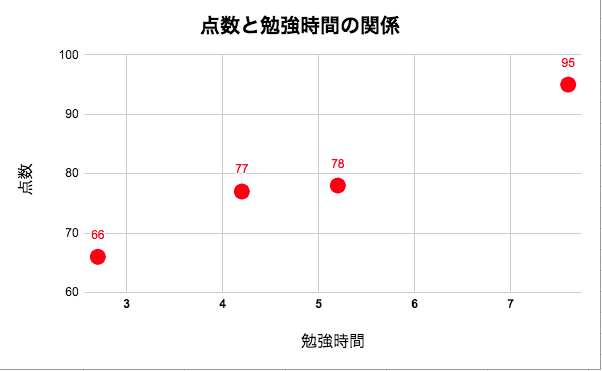
このデータを視覚化すると、下のようなグラフになります。
横軸が勉強時間、縦軸がテストの点数を表しています。
勉強時間が長くなるほど、テストの点数が上がっている傾向がわかります。

4人のデータを用いて、「勉強時間」と「テストの点数」の関係を数式で表します。
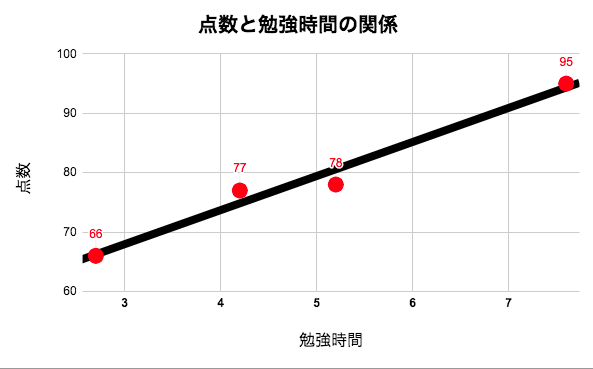
「勉強時間」と「テストの点数」の関係が線形であると仮定して、データに当てはまる直線を下記のように引きます。

黒の直線は下の式(回帰式)で表せます。

y = 5.7x + 51 

この式（回帰式）の意味は、

(点数)= 5.7 × (学習時間) + 51

となります。
学習時間が0のとき、51点となり、１時間勉強するごとに5.7点ずつ点数が上がっていることを意味しています。
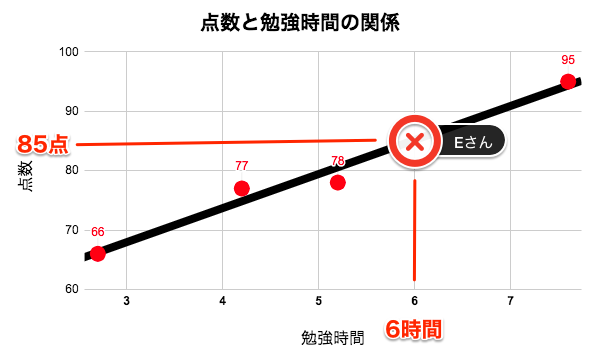
この式（回帰式）を利用することで、勉強時間から、他の生徒がどの程度の点数を獲得できるかが予測できるようになります。
例えば、勉強時間が6時間のEさんの点数は、

\begin{align}
(Eさんの点数) &= 5.7× (学習時間) + 51 \\
&= 5.7 × 6 + 51 \\
&= 85(点)
\end{align}

と求めることができます。

このように、回帰分析は、結果となる数値と要因となる数値の関係を回帰式で表します。
また、要因となる数値を説明変数、結果となる数値を目的変数といいます。
今回の例でいうと、「勉強時間」から「点数」を予測したので、「勉強時間」が説明変数で、「点数」が目的変数となります。

回帰分析のうち、1つの目的変数を1つの説明変数で予測するものを単回帰分析と言います。
そして、1つの目的変数を２つ以上の説明変数で予測するものを重回帰分析と言います。

単回帰分析

y = a + b_1x_1 \\

重回帰分析

y = a + b_1x_1 + b_2x_2 + ・・・ + b_nx_n \\
y:目的変数 \\
a:切片 \\
b:回帰係数 \\
x:説明変数 

重回帰分析では、天気や気温、宣伝費用や暦などの説明変数と、商品の売上数という目的変数の関係を回帰式として表現します。
では、どのようにしてインプットしたデータから、回帰式を算出しているのか。

まずは単回帰分析について、Pythonで実装していきたいと思います。
また、仕組みの理解を目的とするため、scikit-learnやStatsModelsのような機械学習のライブラリを利用しないで実装します。

単回帰分析

単回帰分析は、1つの目的変数を1つの説明変数で予測する分析手法でした。
また、目的変数と説明変数は線形の関係があるという仮定があります。
つまり、目的変数と説明変数は、下記の回帰式で表現できるという仮定があります。

\begin{align}
y &= w_1x + w_0 \\
(目的変数) &= w_1×(説明変数) + w_0
\end{align}

先ほどの例では、

(点数)= 5.7 × (学習時間) + 51

でした。

どのようなアルゴリズムで、5.7という傾きや、51という切片を算出したのか。
勉強時間と点数のデータ(49人分)の学習データを使いながら実装していきます。

まずは、必要なライブラリのimportと、学習データを読み込みます。

今回使用する学習データはこちらをクリック

TestScores_StudyHours_Liner.csv

https://drive.google.com/open?id=1z80g4kKGMMBbnCaAz_iUAYTLkEvz4cZI

Hours	Scores
5.2	78
4.2	77
7.6	95
2.7	66
9.1	91
1.3	59
3.6	72
9.4	100
6.8	88
8.5	89
8.4	98
2.6	71
2.8	66
4	73
6.9	88
5.2	83
7.9	96
4.6	76
5.4	85
5.4	79
5.2	83
4.4	80
2.2	68
2.1	64
3.4	69
1.2	57
0.2	58
2	63
4.7	77
4.5	78
5.5	84
8.3	97
4.3	75
0.9	62
5.8	82
8.2	100
6.1	87
3.3	73
6.3	88
6.6	89
4.5	78
3.8	74
3.8	73
4.7	80
1.5	60
5	81
9.1	91
4.3	74
1.3	58

ちなみに、この記事で書いてあるコードはGoogle colaboratoryで実装しています。
Google colaboratoryは、googleアカウントがあれば、誰でもクラウド上でPythonを実行できるサービスです。説明は要らないから、コードを見たいって人は、下記画像からcolaboratoryに飛べるので、見てください。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data= np.loadtxt("./TestScores_StudyHours_Liner.csv",delimiter=",",skiprows=1)

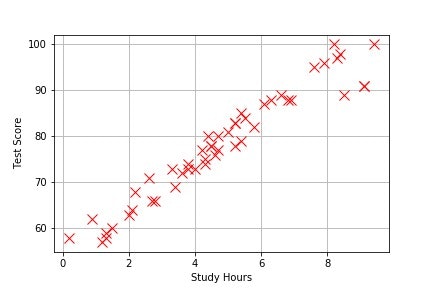
どのようなデータが入っているのか、プロットして確認します。

plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Score')
plt.grid(True)
plt.show()

横軸が勉強時間、縦軸がテストの点数を表していて、49人分のデータがプロットされています。
これらのデータを入力して、直線の傾き(w₁)や切片(w₀)を算出していきます。

y = w_1x + w_0

直線の傾き(w₁)や切片(w₀)を算出するのに、コスト関数(平均二乗誤差)と最急降下法を用います。

コスト関数(平均二乗誤差)

コスト関数(平均二乗誤差)は、ある回帰式が学習データとどれだけフィットしているかを定量的に評価します。
もう少し具体的にいうと、コスト関数はモデルが算出した予測値と学習データの実際値の差(残差)を計算します。

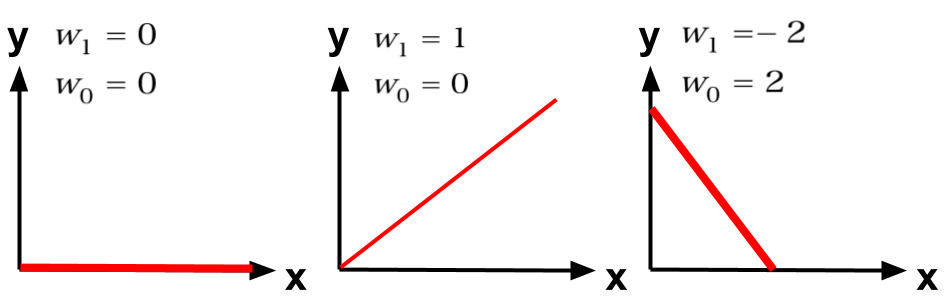
例えば、(w₀,w₁) = (0,0)　のときの、回帰式は下記のようになります。

\begin{align}
y &= w_1x + w_0 \\
y &= 0 
\end{align}

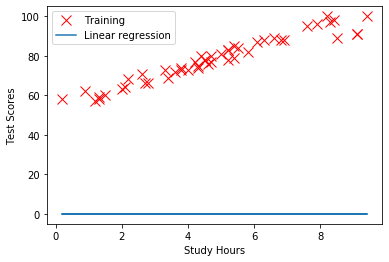
このときの、回帰式と学習データの関係を視覚化すると、下のグラフになります。

w0,w1 = 0,0
plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Scores')

plt.plot(data[:,0],data[:,0]*w1 + w0,'-',label='Linear regression')
plt.legend()
plt.show()

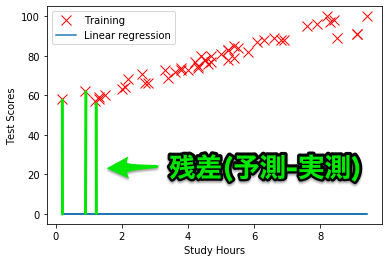
青い線が、(w₀,w₁) = (0,0)　のときの回帰式、赤×が学習データです。

【補足】係数と直線の関係

補足ですが、(w₀,w₁)=(0,0)(0,1)(2,-2)のときの直線は下のようになります。

y = w_1x + w_0 \\

コスト関数は、残差{(予測した値)-(実際の値)}を、それぞれのデータで計算し、全ての残差の和を計算します。

(w₀,w₁) = (0,10)のときは、こちらが残差になります。

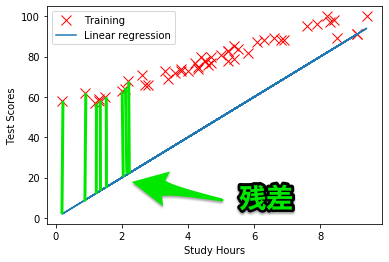
コスト関数は、平均二乗誤差を計算します。
学習データそれぞれの残差の二乗を計算し、その総和を、2×テータ数で割った値がコストとなります。
式で表現すると、

\begin{align}
J(w_0,w_1) &= \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}-y)^2 \\
 &= \frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2
\end{align}

\begin{align}
m &: データ数 (m=49) \\
\hat{y} &: 予測値 (\hat{y}=w_1x + w_0) \\
y &: 実測値
\end{align}

では、(w₀,w₁) = (0,0)　のときのコストを計算して見ます。
まずは、コスト関数を定義します。

# コスト関数
def cost_function(w0,w1,data):
    cost = 0
    m = len(data)
    for i in range(m):
        x = data[i,0]
        y = data[i,1]
        cost += ((w1 * x +w0) -y)**2
    cost = cost / (2*m)
    return cost

(w₀,w₁) = (0,0)　のときのコストは、

w0,w1 = 0,0
cost_0_0 =cost_function(w0,w1,data)
print(cost_0_0)
#3128.3979591836733

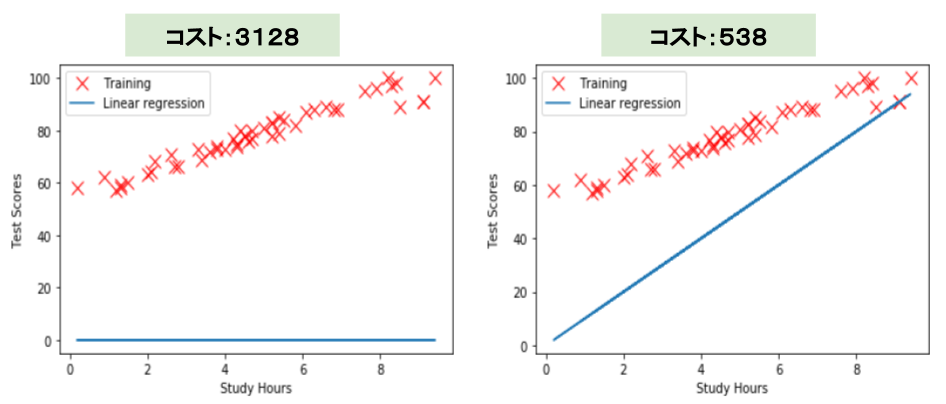
3128と求めることができました。

w₀,w₁ = 0,10のときのコストも求めます。

w0,w1 = 0,10
cost_0_10 =cost_function(w0,w1,data)
print(cost_0_10)
#538.9285714285714

コストは、538と求められました。

左の画像と右の画像の直線を見比べると、右のw₀,w₁ = 0,10のときの回帰式のほうが学習データに近いことが、視覚的にわかります。
また、コスト関数を比べても、左のコストが3128に対して、右のコストが538と、コストが大幅に減少していることがわかります。
このように、回帰式が学習データとフィットしているかは、コスト関数を用いることで、定量的に評価できます。
単回帰分析においてのモデルの学習とは、コストが最小となる回帰係数を算出することです。

そして、コストが最小となる回帰係数を算出するのに、ポイントとなるのが、最急降下法です。

最急降下法

最急降下法は、関数を最小にするようなパラメーターを求めるためのアルゴリズムです。
今回はコスト関数から得られるコストを最小にするような回帰係数（w₀,w₁)を求めたいです。

コスト関数は下記の式でした。

\begin{align}
J(w_0,w_1) &= \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}-y)^2 \\
 &= \frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2
\end{align}

\begin{align}
m &: データ数  \\
\hat{y} &: 予測値 (\hat{y}=w_1x + w_0) \\
y &: 実測値
\end{align}

コスト関数をw₀で偏微分すると、

\begin{align}
\frac{\partial }{\partial w_0}J(w_0,w_1) &= \frac{\partial }{\partial w_0}\frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2 \\
&= \frac{1}{m}(w_1x + w_0-y)
\end{align}

コスト関数をw₁で偏微分すると、

\begin{align}
\frac{\partial }{\partial w_1}J(w_0,w_1) &= \frac{\partial }{\partial w_1}\frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2 \\
&= \frac{1}{m}(w_1x + w_0-y)x
\end{align}

と求めることができます。
偏微分をすると、コスト関数の傾きがわかります。
コストが小さくなるように、w₀,w₁を更新したいので、元々の回帰係数から偏微分で得られた値を引きます。

\begin{align}
w_0 &:= w_0 - \alpha\frac{1}{m}(w_1x + w_0-y) \\
w_1 &:= w_1 - \alpha\frac{1}{m}(w_1x + w_0-y)x
\end{align}

\begin{align}
\alpha &:学習率 \\
m &:データ数 \\
x &:説明変数 \\
y &:目的変数 \\
\end{align}

αは学習率と呼ばれ、回帰係数を更新する値の大きさを調整します。
学習率は、大きすぎると回帰係数が収束しない可能性があり、また、小さすぎると、回帰係数の収束に時間がかかってしまいます。
今回は学習率=0.01でと決めて、進めていきます。

では、最急降下法を実装していきます。

# 最急降下法(Gradient Descent)
def gradientDescent(w0_in,w1_in,data,alpha):
    w0_gradient,w1_gradient = 0,0  #初期値
    m = float(len(data))           #データ数
    for i in range(len(data)):
        x,y = data[i,0], data[i,1]
        w0_gradient += (1/m) * (((w1_in * x) + w0_in) -y)
        w1_gradient += (1/m) * ((((w1_in * x) + w0_in) -y) * x)
    w0_out = w0_in - (alpha * w0_gradient) #回帰係数の更新
    w1_out = w1_in - (alpha * w1_gradient) #回帰係数の更新
    return [w0_out, w1_out]

w0_gradient、w1_gradientは、初期値0を設定しています。
また、α、w₀、w₁、学習回数の初期値を設定します。

alpha = 0.01
init_w0,init_w1 = 0,0
iterations = 1000 #学習回数

それではコスト関数と最急降下法を用いて、単回帰分析のモデルの学習を定義していきます。
今回は、1000回の回帰係数の更新する中で、コストがどのように推移するかを可視化するために、J_historyを追加します。

def run(data,init_w0,init_w1,alpha,iterations):
    w0,w1 = init_w0,init_w1
    J_history = [] #コストの履歴を格納用
    for i in range(iterations):
        w0,w1 = gradientDescent(w0,w1,np.array(data),alpha)
        J_history.append(cost_function(w0,w1,data)) #コストの履歴をJ_historyに追加
    return [w0,w1, J_history]

それでは、モデルの学習（コストが最小となる回帰係数の算出）をします。

[w0,w1, J_history] = run(data,init_w0,init_w1,alpha,iterations)
print("w0 = {} /w1 = {}".format(w0,w1))
#w0 = 47.325313552065204 /w1 = 6.135761014127023

回帰係数を求めることができました。

\begin{align}
y &= w_1x + w_0 \\
  &= 6.13x + 47.3 \\
\end{align}

この式とつまり、

(テストの点数)= 6.13×(勉強時間) + 47.3 

ということを意味しています。
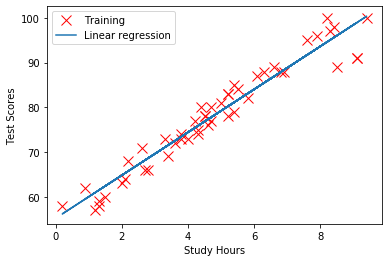
また、回帰式と学習データを視覚化すると、

plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Scores')

plt.plot(data[:,0],data[:,0]*w1 + w0,'-',label='Linear regression')
plt.legend()
plt.show()

このように、学習データにフィットした直線を描くことができました。

また、コストの推移も確認してみましょう。

# コストと学習回数のグラフ
plt.plot(range(len(J_history)),J_history,"-b",linewidth=1)
plt.xlabel("Number of Iterations")
plt.ylabel("Cost J")
plt.grid(True)
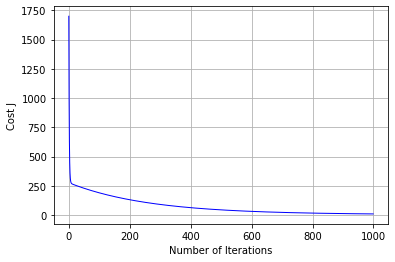
plt.show()

縦軸がコストで、横軸が学習回数を表しています。
学習を繰り返すごとに、コストが下がっているのがわかります。

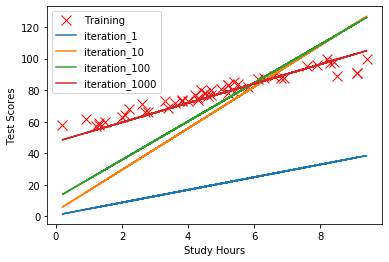
学習回数を1000回と決めてしまいましたが、学習回数が1回、10回、100回、1000回のときに算出される回帰式を比較してみました。

iterations_ = [1,10,100,1000]

plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Scores')

for iteration in iterations_:
    [w0,w1, J_history]  = run(data,init_w0,init_w1,alpha,iteration)
    plt.plot(data[:,0],data[:,0]*w1 + w0,'-',label='Linear regression_{}'.format(iteration))

plt.legend()
plt.show()

学習を繰り返すごとに、回帰式が学習データを捉えられるようになっていることがわかります。

まとめ

単回帰分析は、目的変数と説明変数が線形の回帰式で表現できるという仮説がある。

y = w_1x + w_0 

ある回帰係数（w₀、w₁）のときの回帰式が、学習データにどれだけフィットしているかはコスト関数を用いて評価する。
最急降下法を用いて、コストが小さくなるような回帰係数を算出する。

あとがき

今日は単回帰分析についてのまとめを書きました。
本当は重回帰分析について書きたかったのですが、単回帰分析だけで結構長くなってしまったので、別記事にします。
最後まで読んでいただきありがとうございました。