市場データからボラティリティ・スマイルを確認してみた

金融工学の本を読むと，しばしばボラティリティ・スマイルについて言及されています．ただ，自分の手で計算してみないとわかった気にならない性質なので，そもそもボラティリティ・スマイルとは何かから始め，実際にグラフで確認してみました．なお，すべての実装はgithub (https://github.com/yotapoon/volatility_smile )にアップしているので，実装だけ確認したい人はこちらをご覧ください．

ボラティリティ・スマイルとは

まず問題設定を明確にし，いくつか用語を定義してからボラティリティ・スマイルを説明します．問題設定は端折っている部分も多いため， 知識が足りない方はぜひhttps://qiita.com/yotapoon/items/30c1bc411c5a8f08d219 を参照してください．ご存知の方は飛ばしていただいて構いません．

問題設定

いま注目する原資産の価格が$S(t)$なる確率過程であらわされるものとします．期待収益率を$\alpha$，ボラティリティ(要するに変動率)を$\sigma$とすれば，$S(t)$は以下の幾何ブラウン運動に従うものとモデル化できます：

$$
dS(t) = \alpha S(t) dt + \sigma S(t) dW(t)
$$

ただし$W(t)$はブラウン運動で，$dW(t)$は平均$0$，標準偏差$\sqrt{dt}$の正規分布に従うといえます．
また，単位時間当たり$r$の成長率を持つ安全資産の存在を仮定します．$r$は金利と考えることができます．

次に，ヨーロピアン・コールオプションを定義します．ヨーロピアン・コールオプションを購入するとは，「時刻$t = T$において，原資産の価格$S(T)$によらず，行使価額$K$で原資産を1単位取得できる"権利"を購入する」ということです．数式にまとめると，時刻$t = T$において

$$
c(T, S(T)) = (S(T) - K)^+
$$

という価格となるような商品だと考えられます．ただし，$(x)^+$は$x \geq 0$のとき$x$を返し，$x < 0$のとき$0$を返す関数です．
同様にヨーロピアン・プットオプションは，時刻$t = T$において

$$
p(T, S(T)) = (K - S(T))^+
$$
という価格となるような商品だといえます．

$t = 0$時点においてこれらの商品を売買するためには，$c(t=0, S(0))$や$p(t=0, S(0))$の値(つまり価格)を決める必要があります．無裁定価格理論を用いると，一般に$t = 0$の時点以外においても価格を決定することができ，

c(t, x) = x \Phi(d_+(T-t, x))) - K e^{-r(T-t)} \Phi(d_-(T-t, x)) \\
p(t, x) = -x \Phi(-d_+(T-t, x))) + K e^{-r(T-t)} \Phi(-d_-(T-t, x))

という形となります．ただし，

d_{\pm} (\tau, x) = \dfrac{1}{\sigma \sqrt{\tau}} \left[ \log \dfrac{x}{K} + \left( r\pm \dfrac{1}{2} \sigma^2 \right) \tau \right] \\
\Phi(x) = \dfrac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-x'^2/2} dx'

を導入しました．

インプライド・ボラティリティ

コールオプションの価格$c(t, S(t))$を決定する式をよく見ると，計算するために必要な量は①満期までの時間$T-t$，②原資産価格$S(t)$，③行使価額$K$，④ボラティリティ$\sigma$，⑤金利$r$であることがわかります．この中で，④ボラティリティ$\sigma$の値は，契約時点$t = 0$において正確にはわからず，推定するしかありません．一方で，コールオプションの価格$c(0, S(0))$は市場を観察することで決められます．ゆえに，コールオプションの価格$c(t, S(t))$を決定する式の左辺に，市場で観察された値($c^*$としましょう)を代入することで，ボラティリティ$\sigma$を推定することができます．つまり，以下の式を$\sigma$に関する方程式として解くのです．

c^* = x \Phi(d_+(T, x))) - K e^{-rT} \Phi(d_-(T, x)) \\
d_{\pm} (T, x) = \dfrac{1}{\sigma \sqrt{T}} \left[ \log \dfrac{x}{K} + \left( r\pm \dfrac{1}{2} \sigma^2 \right) T \right] \\

(細かい人のための追記)

細かい人は解の一意性などが気になるかもしれませんが，$c(t, S(t))$が$\sigma$に関して単調増加であるという性質を考えると，解の一意性は直ちにわかります．さらに，これはニュートン法などのアルゴリズムが適用可能であることも示唆しています．

以上の手続きにより推定されたボラティリティ$\sigma$を，**インプライド・ボラティリティ**と呼びます．これは，市場により「暗示された(implied)」ボラティリティであるということを意味しています．

ボラティリティ・スマイル

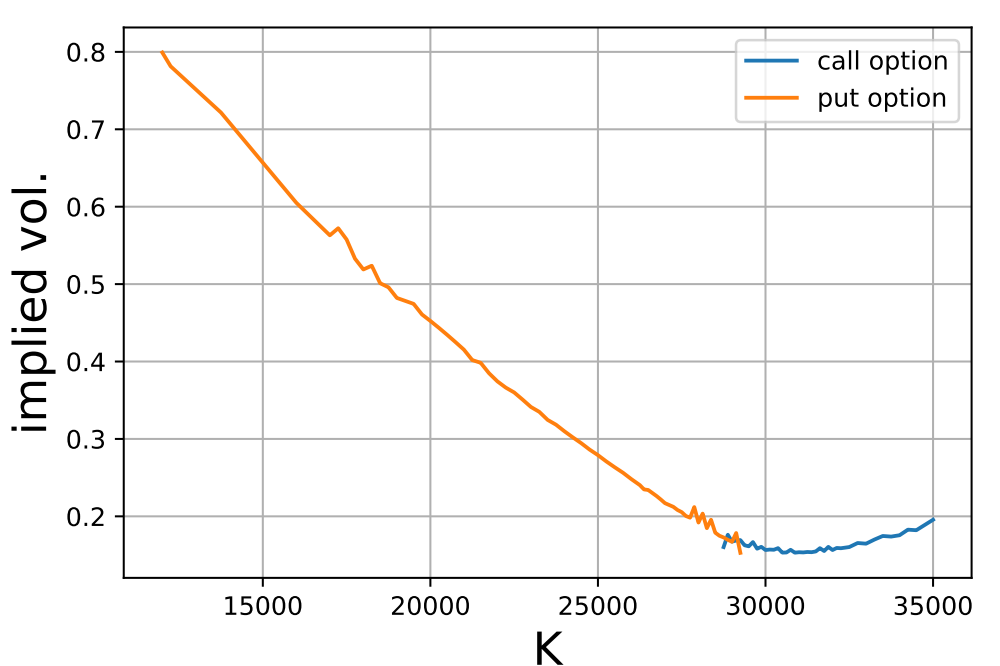
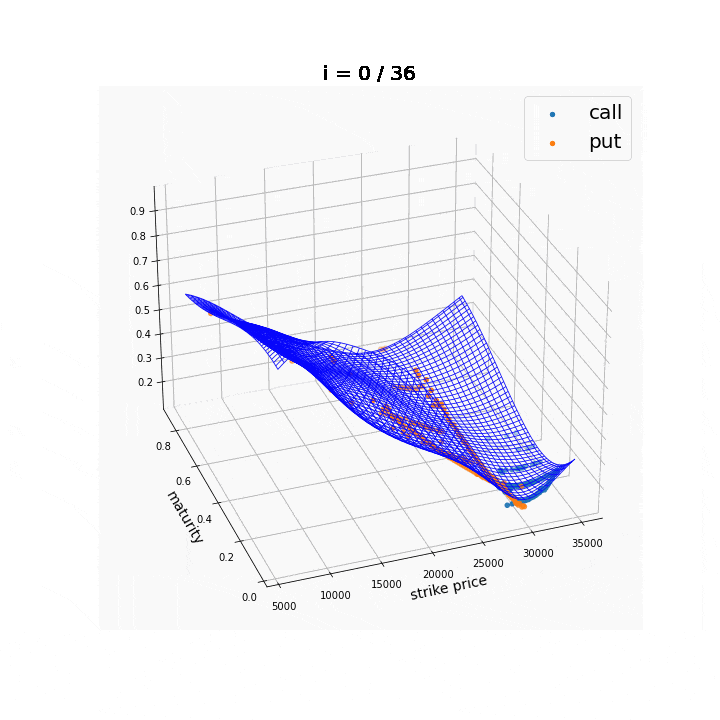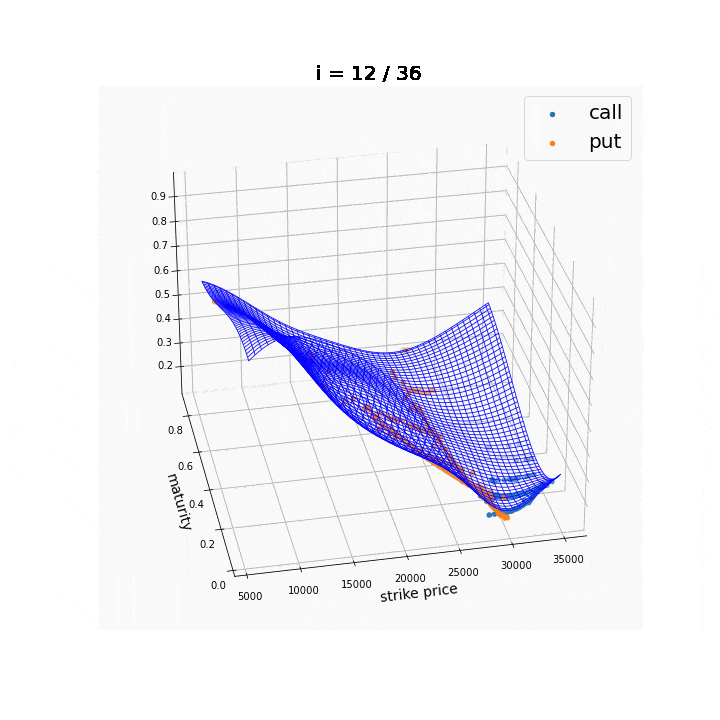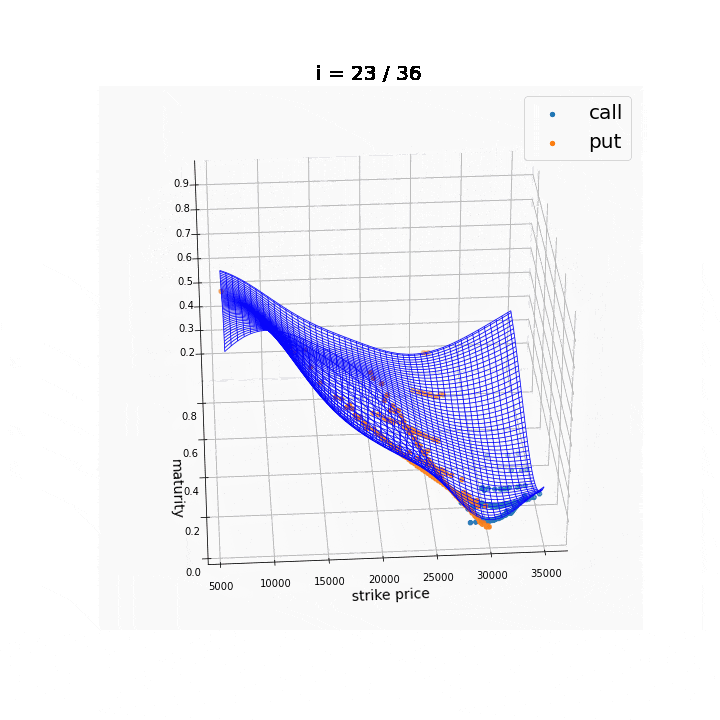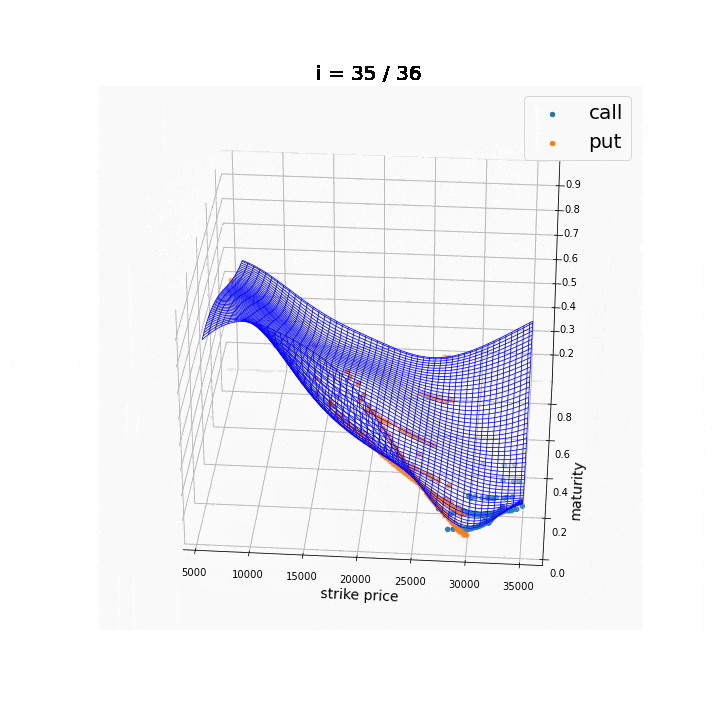
長くなってしまいましたが，ようやく本題であるボラティリティ・スマイルを説明できます．前述のインプライド・ボラティリティ$\sigma$を，行使価額$K$の関数として描いてみたものが下図です．計算の詳細は後述します．

グラフから，明らかに凸関数の形状をしていることが確認できます．これが人の笑っている顔に見えることから，ボラティリティ・スマイルという名前がついています(いうほど見えるか？)．もともとのモデルでは，原資産のボラティリティ$\sigma$は行使価額と全く無関係に決まっていたにも関わらず，このような非自明な関係が生じていることに注意します．
さらに，①計算時点(2021年4月28日)での原資産価格(日経平均)$S(0) = 29053.97$付近から離れるほど，インプライド・ボラティリティが大きくなっていること，および②全体的に右下がりになっていることも重要です．これらの性質は，満期が短い株式オプションに典型的にみられるものです．
ボラティリティ・スマイルの原因は，「市場参加者が想定している原資産価格$S(t)$の変動は，ブラックショールズモデルで仮定したものと一致していないため」だそうです．より詳しい解説をQuant Collegeの中の方がされているので，ぜひご覧ください( https://quantcollege.net/smile-pricing-volatility-smile-explained )．

インプライド・ボラティリティの計算

まず，インプライド・ボラティリティを計算するための手続き，及びニュートン法によるアルゴリズムを示します．また，日本取引所の公開しているデータ( https://www.jpx.co.jp/markets/derivatives/option-price/index.html )を使って，実際にボラティリティ・スマイルを確認します．

データの確認

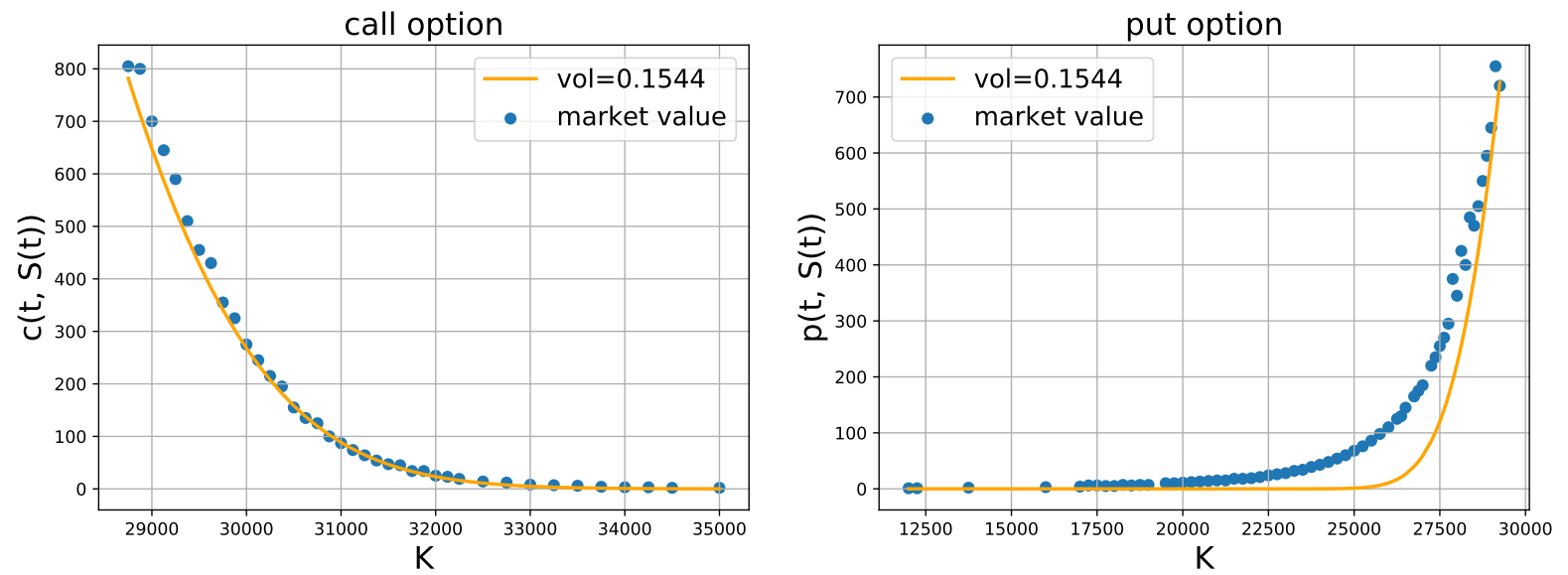
日本取引所の公開しているデータから，日経225の2021年6限月(つまり原資産を日経225とし，2021年6月の第二金曜日に満期を迎えるオプション)の，2021年4月28日における終値を抽出しました．データの整形などは本題ではないため割愛します．行使価額$K$と，コール・プットそれぞれの価格の関係を以下に示します．

なお，データによると原資産価格は$S(0) = 29053.97$，基準ボラティリティ(?)は$\sigma = 0.1544$だそうです．$\sigma = 0.1544$としてオプション価格をプロットしたものも同時に示しました．コールオプションに関しては良い近似になっているものの，プットオプションでは乖離が生じています．また，$\sigma$の値を変えてみても，プットオプションの乖離は改善されなかったことにも触れておきます．
目標は，行使価額$K$の値ごとに決まる市場価格$c^*$を用いて，インプライド・ボラティリティ$\sigma$を計算することです．

ニュートン法によるインプライド・ボラティリティの計算

まず，コールオプションに関してインプライド・ボラティリティ$\sigma$をどのように求めるか考えてみます．そのために，コールオプションの価格$c(t, S(t))$を$c(K, \sigma)$のように書き直しておきます．いまの目標は，行使価額$K$とそれに対応する市場価格$c^*$から

$$
c^* = c(K, \sigma)
$$
を満たすようなボラティリティ$\sigma$を求めることです．
ここで，$c(K, \sigma)$を$\sigma$で微分した値

$$
\nu(K, \sigma) = \dfrac{\partial c}{\partial \sigma} = S(0) \sqrt{T} \dfrac{1}{\sqrt{2 \pi}} \exp \left[ -\dfrac{1}{2} d_+^2 \right] > 0
$$
に注目します．ベガと呼ばれるこの値は明らかに正であり，ゆえに$c(K, \sigma)$はボラティリティ$\sigma$に対して単調増加です．よって，以下に示すニュートン法で数値解を得ることができます：
$$
\sigma_t = \sigma_{t-1} - \dfrac{c(K, \sigma_{t-1}) - c^*}{\nu(K, \sigma_{t-1} )}
$$
ただし，初期値$\sigma_0$が小さいとベガ$\nu(K, \sigma)$が$0$に近づいてしまい，うまく計算できないことがあるため，$\sigma_0$は大きくとることをお勧めします．
なお，プットオプションについてもベガは同じ値を取ることが示せます(これはプット・コールパリティから直ちにわかります)．そのためほとんど同様の手続きで，プットオプションの市場価格からもインプライド・ボラティリティを計算することができます．

実装

インプライド・ボラティリティを計算する手順がわかったので，実装します．get_implied_volがインプライド・ボラティリティを計算するメソッドです．

import numpy as np
from scipy.stats import norm 

S0 = 29053.97 # initial stock price
r = 0.00 # interest rate
T = 44 / 365.0 # 1 year

class European_call:
    def __init__(self, S0, r, T):
        self.S0 = S0
        self.r = r
        self.T = T
        
    def get_d_list(self, K, vol):
        d_plus = (1.0 / (vol*np.sqrt(self.T))) * (np.log(self.S0/K) + (self.r+0.5*vol*vol)*self.T)
        d_minus = (1.0 / (vol*np.sqrt(self.T))) * (np.log(self.S0/K) + (self.r-0.5*vol*vol)*self.T)
        return [d_plus, d_minus]
    
    def get_value(self, K, vol):
        d_plus, d_minus = self.get_d_list(K, vol)
        return self.S0*norm.cdf(d_plus) - K*np.exp(-self.r*self.T)*norm.cdf(d_minus)
    
    def get_vega(self, K, vol):
        d_plus, d_minus = self.get_d_list(K, vol)
        return self.S0*np.sqrt(T)*(1.0/np.sqrt(2.0*np.pi))*np.exp(-0.5*d_plus*d_plus)
    
    def get_implied_vol(self, c_actual, K, num_iteration = 80): # c_actual:コールオプションの市場価格
        implied_vol = 1.6 # 小さい値を取るとvegaが0になってしまい，ニュートン法に支障をきたす．
        for idx in range(num_iteration):
            # ニュートン法により，オプションの理論値と市場価格が等しくなるようなsigma_impliedを求める．
            implied_vol = implied_vol - (self.get_value(K, implied_vol)-c_actual) / self.get_vega(K, implied_vol)
        return implied_vol

以下の図は，このプログラムを利用して得られたインプライド・ボラティリティを示したものです．ただしcall option，put optionはそれぞれコールオプション，プットオプションの市場価格$c ^ *$，$p ^ *$から計算したインプライド・ボラティリティです．それぞれのオプションごとに，価格データが存在する行使価額の範囲が大きく異なっているため，カバーする領域も異なっています(「データの確認」の項を参照のこと)．

おまけ

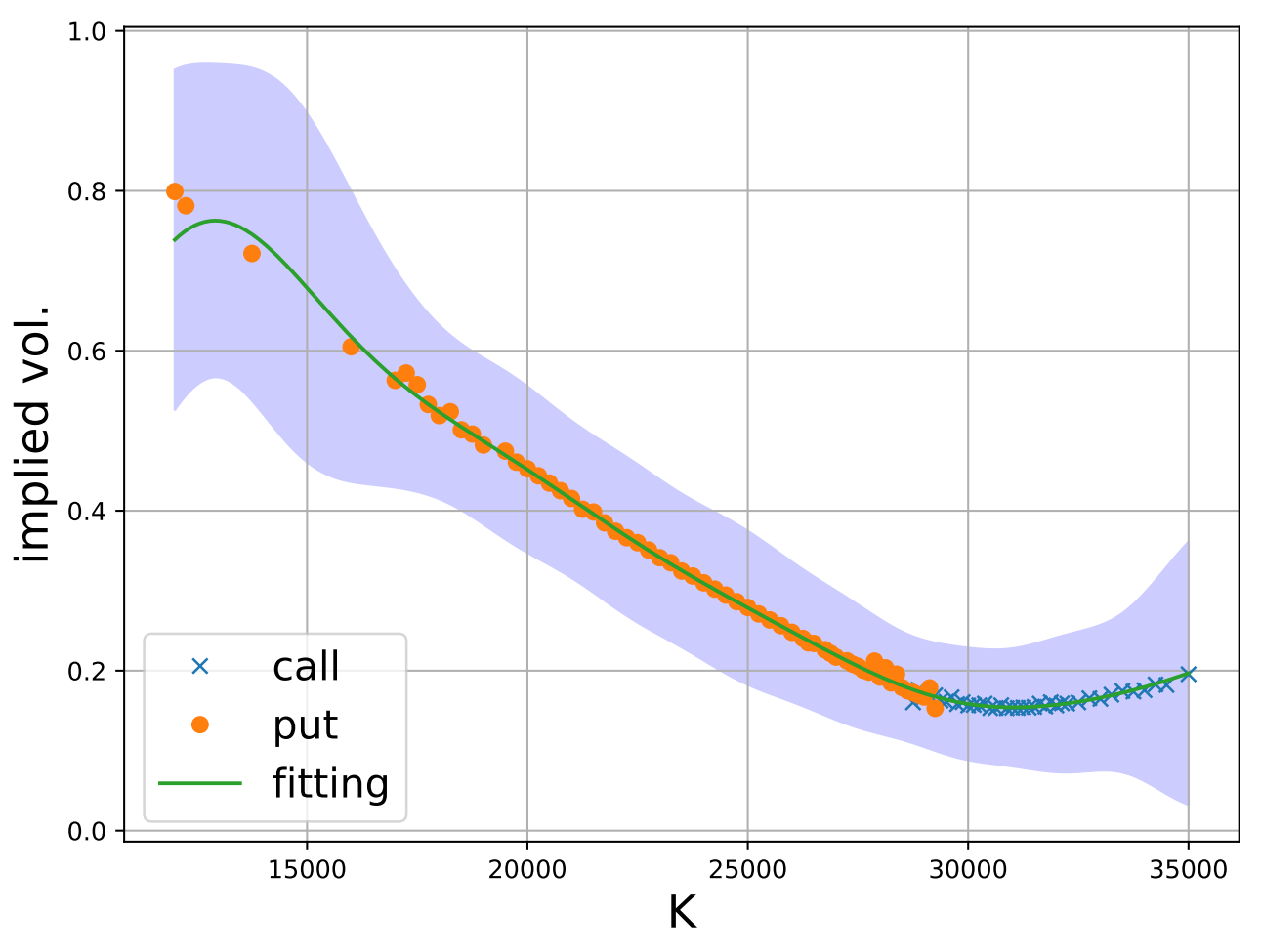
もともとのデータに飛びがあるため，上のボラティリティ・スマイルの図は少しガタついています．せっかくなので，簡単な回帰によって図をきれいにしてみました．

いい感じになっていることがわかります．
なお，今回は行使価額$K$の関数としてのみ扱いましたが，満期までの時間$T$についても同様にインプライド・ボラティリティを計算することができます．このようにして得られる$\sigma(K, T)$のような平面を，ボラティリティ・サーフェスと呼びます．
(2021/5/8追記)
今回の内容を少しいじることで，実装することができました．補完にはガウス過程回帰を使っています．