ブラックショールズ方程式の理論とPythonによる実装

去年インターンでブラックショールズ方程式を理解して実装する必要があったのですが，日本語で金融工学初心者向けのまとまった解説がなく困ったことがありました．そこで，当時のことを思い出しつつ，初心者向けのブラックショールズ方程式の導出および実装を示そうと思います．実装が知りたい人は（ヨーロピアンコールオプションの実装）に飛んでください．

ヨーロピアン・コールオプションとは

まず数学的なモデルに基づき問題を設定し，次にインターンの際に抱いた疑問と自分なりの解答を示します．

問題設定

いま注目する原資産(日経平均でもTOPIXでも特定の銘柄でもいいでしょう)の価格が$S(t)$なる確率過程で表されるとします．期待収益率を$\alpha$，ボラティリティ(変動率)を$\sigma$とすれば，$S(t)$は以下の確率微分方程式(幾何ブラウン運動)に従うものとモデル化できます：
$$
dS(t) = \alpha S(t) dt + \sigma S(t) dW(t)
$$
ただし$W(t)$はブラウン運動とし，以下のような性質を持ちます．

• 任意の$t_1 < \cdots < t_n$に対し，$W(t_1)-W(0)$，$W(t_2)-W(t_1)$，$\cdots$，$W(t_n)-W(t_{n-1})$は独立．
• 任意の$t > s$に対し，$W(t)-W(s)$は正規分布${\mathcal N}(0,t-s)$に従う．

そのため，非常にラフにいうと，$dW(t)$は平均$0$，標準偏差$\sqrt{dt}$の正規分布に従うと言えるでしょう．

(細かい人のための追記)

細かい人は，数値計算の際に$dt$と$dW(t)$のスケールが異なる点が気になるかもしれません．平方根を取っているため，微小量$dt$に対しては$dW(t)$の方が圧倒的に大きくなってしまいます．しかし，あくまで$dW(t)$は乱数であり，数値計算上は大量に足し算することになるため，長期的に見た際にはスケールの問題は生じなくなります(中心極限定理を思い浮かべればいいかもしれません)．確率解析の目線では，「ファイナンスのための確率解析II」練習問題4.14が本質的だと思います．

以下に$S(t)$のサンプルパスを示します．確かに株価っぽい動きになっています．

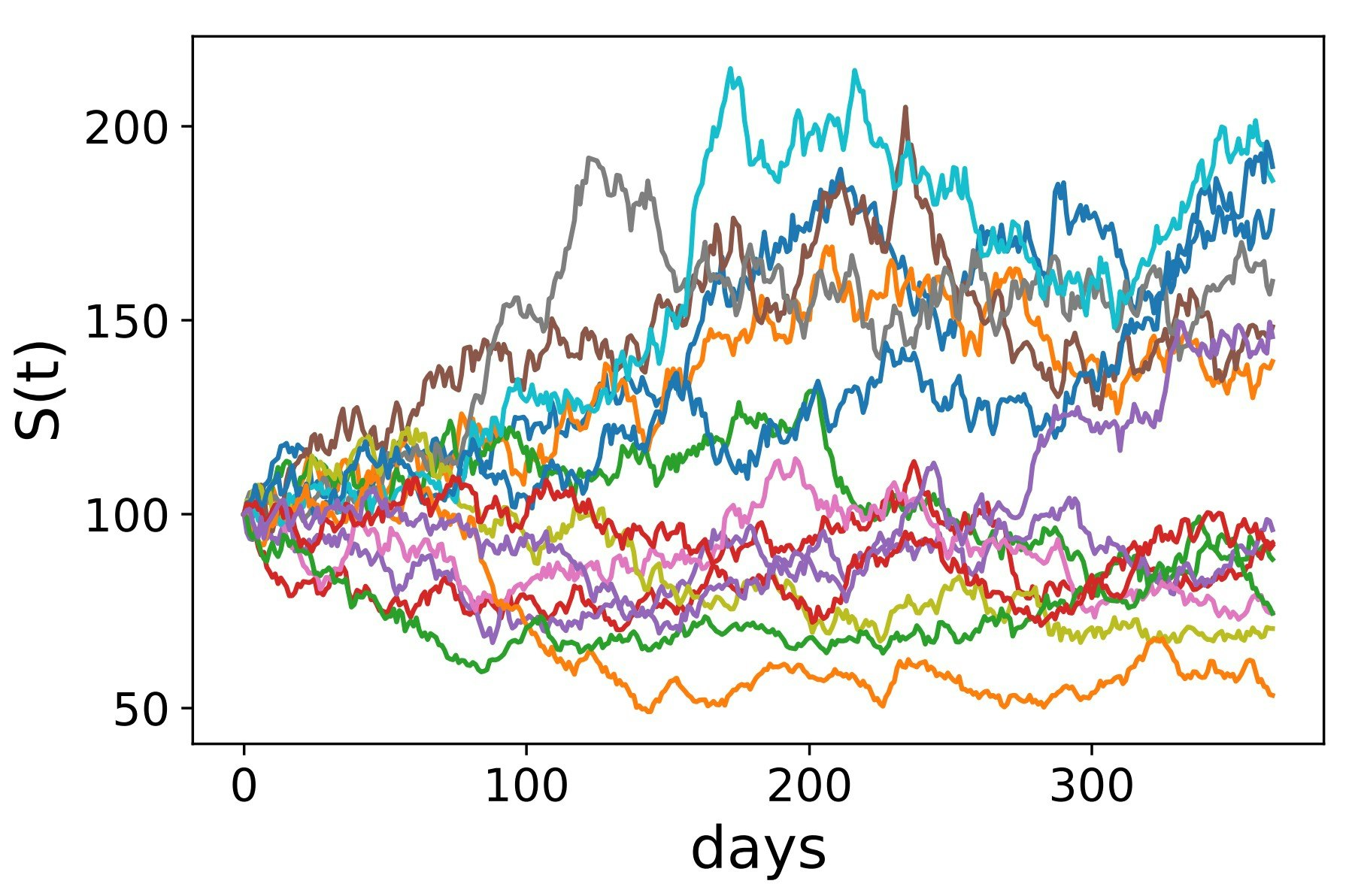
ここで，ヨーロピアン・コールオプションを定義します．ヨーロピアン・コールオプションを購入するとは，「時刻$t=T$において，原資産の価格$S(T)$によらず，行使価額$K$で原資産を1単位取得できる"権利"を購入する」ということです．$S(T) > K$のとき，権利を行使して原資産を得て，直ちに売ることで$S(T)-K$の利益が得られます．一方$S(T) < K$のとき，権利を行使することもできますが，実際の価格$S(T)$より高い価格$K$を支払うのは明らかに無駄です．よって，権利を放棄することになります．
以上をまとめると，時刻$t = T$におけるヨーロピアン・コールオプションの"価値"は以下のようになります：
$$
(S(T) - K)^+
$$
ここで$(x)^+$は$x \geq 0$のとき$x$を返し，$x < 0$のとき$0$を返す関数です．また定数$K$を行使価額と呼びます．
いま，時刻$t=0$におけるヨーロピアン・コールオプションの価格を決めるというのが問題です．

いくつかの疑問

• そもそもヨーロピアン・コールオプションの何がうれしいのか

例えば，ある企業の株式を一年後に所有したいと考える投資家がいるものとします．ただし，いま購入してしまうと，一年後には価格が下落しており損をしてしまう可能性があります．また購入しないままでいると，一年後には手が出ないような価格になってしまっている可能性もあります．ヨーロピアン・コールオプションを購入すると，価格が下落していれば権利を放棄，価格が上昇していれば権利を行使することで，これらのリスクを回避(ヘッジ)できます．いわばコールオプションは一種の"保険"のようなものになっており，その対価としてプレミアム(ここではヨーロピアン・コールオプションの価格)を支払うことになります．

(より実践的な例)

より実践的な例として，すでに原資産を有している投資家がコールオプションを"売る"ことを考えます．このとき，オプションを買うときとは反対に，投資家はプレミアムを手にすることになります．そのため，原資産の価格が少し下落しても，プレミアムによってその損失を補うことができます．また原資産の価格が上昇し権利行使価額を上回ると，コールオプションの売却先が権利を行使することになります．しかしこの場合はこちらも原資産に利益が出ているため，プレミアム分だけ利益が残ることになります．以上のような戦略はカバード・コールと呼ばれており，詳しい解説も多いのでそちらも参考にしてください．さらに後述のプット・オプションと組み合わせることで，原資産の変動が大きいとリターンが得られるストラングルの買いなど，非常に多様な戦略が生まれます．

以上のように，投資家に様々な戦略が生まれるという点がオプションの利点です．

• とりあえず高い値段で売っておけばいいのでは？

とインターンのときは思いましたが，その場合自分が高い値段で買い取らなければなりません．これが相手にとっての裁定機会(要は手元0円で初めて絶対に損をしない戦略)を与えることになってしまいます．相手方にとっての確実な利益はこちらにとっての確実な損失となるため，何としても避ける必要があります．
下手な絵で恐縮ですが，ここはややこしいので図にしてみました．

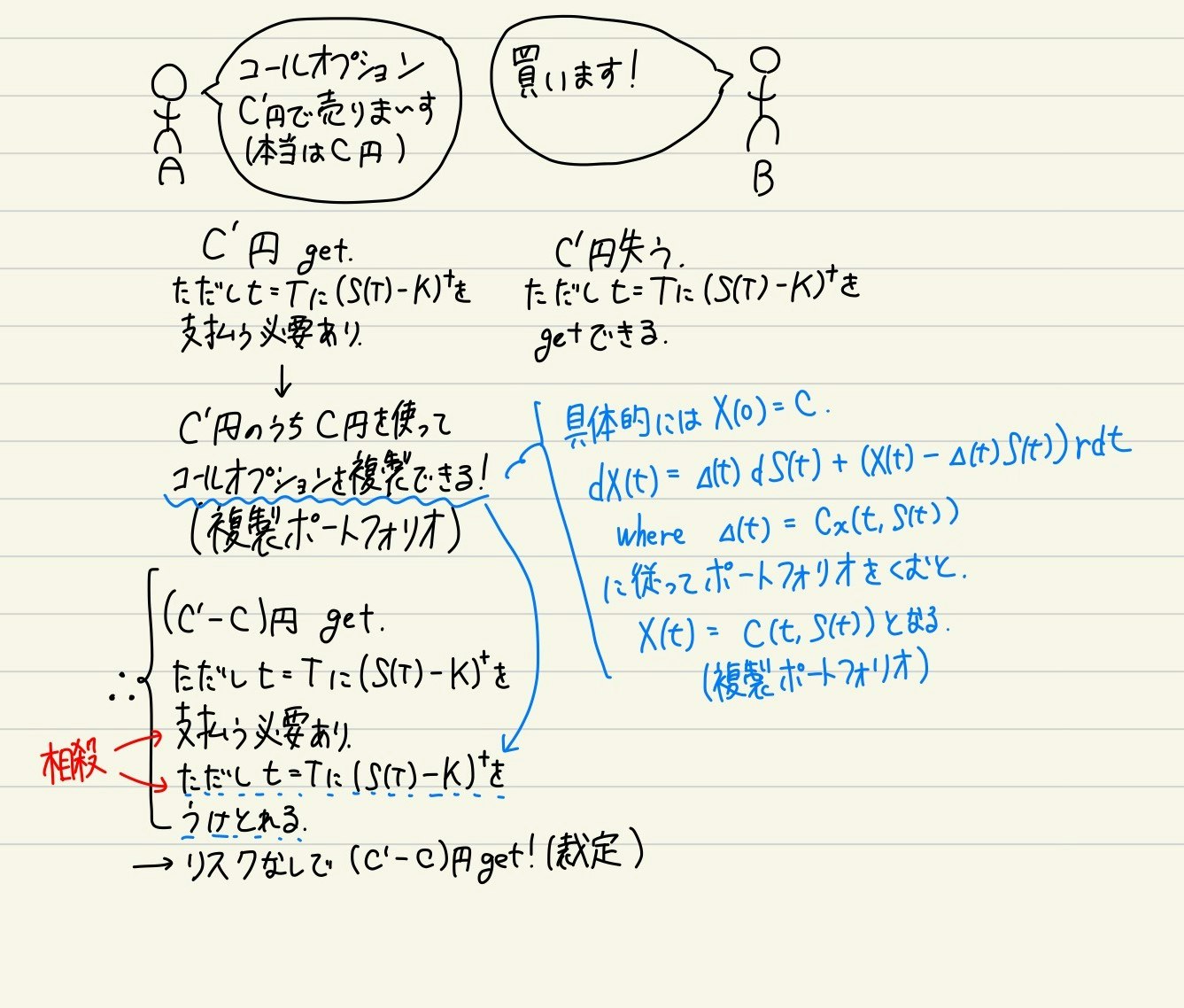
(裁定機会となる理由)

コールオプションの実際の価格$c$よりも高い値段$c'$で売りつけることができたとします．後述しますが，実際の価格$c$と同額の資金を用意し適切に運用することで，ヨーロピアン・コールオプションと同じキャッシュフローを再現できます．よって，コールオプションを売りつけた先の利益と同額の利益を出すことができるため，コールオプションの売りによる損失(あるいは利益)を完全に相殺できます．その際，余った資金$c'-c$は手元に残り，純粋な利益となります．つまり，絶対に損をしない戦略となっているわけです．裁定について理解するには，「ファイナンスのための確率解析I」や「Frequently Asked Questions in Quantitative Finance」がおすすめです．

ブラックショールズ方程式の導出

時刻$t$において原資産価格が$S(t)$であるときの，ヨーロピアン・コールオプションの価値を$c(t,S(t))$とします．求めたいのは$t=0$における価値$c(0,S(0))$ではありますが，まず$c(t,x)$の満たすべき方程式から求めることにします．これは同時に，以下で述べる複製ポートフォリオをどのように構成すればよいかの方針も与えてくれます．

複製ポートフォリオ

仮定として，手元の資金$X(t)$を原資産と債券のみに投資できるものとします．ここで急に債券が出てきたのが謎に思えるかもしれませんが，これは"ほぼ確実に損をしない投資対象"の典型例として用いているだけです．わかりにくければ，銀行に預けていると考えてもよいでしょう．また，債券の期待成長率(あるいは金利)を$r$とします．
いま初期資産$X(0)$から始めて，ヨーロピアン・コールオプションの価値$c(t,S(t))$を再現したいとしましょう．各時刻において$\Delta(t)$単位だけ原資産を保有し，残りを銀行に預けることにより実現できたとすると，この保有割合(あるいは戦略)$\Delta(t)$を複製ポートフォリオと呼びます(ポートフォリオとは"財布"を意味するイタリア語に由来するそうです)．
この場合，手元の資産$X(t)$の時間変化は以下のように与えられます：
$$
dX(t) = \Delta(t) dS(t) + r(X(t) - \Delta(t) S(t) ) dt
$$
第一項は原資産の価格変動による利益，第二項は銀行への預け入れによる利子による利益を表します．

ヨーロピアンオプションの価値の推移

一方で，ヨーロピアン・コールオプションの価値$c(t,S(t))$は伊藤の公式から以下のように時間変化します：
$$
dc(t,S(t)) = c_t(t,S(t)) dt + c_x(t,S(t)) dS(t) + \dfrac{1}{2} c_{xx}(t,S(t)) dS(t) dS(t)
$$
伊藤の公式が適用できる条件について説明すると非常に長くなるので省略しますが，今回のモデル化では全く問題ありません．また，期待収益率$\alpha$やボラティリティ$\sigma$が時間変化する場合であっても適用できます．
有名な伊藤ルール($dt dW(t) = 0$，$dW(t) dW(t) = dt$，$dt dt = 0$)に基づき第三項を少し計算すると，以下が得られます：
$$
dc(t,S(t)) = c_x dS(t) + \left( c_t + \dfrac{\sigma^2}{2} S(t)^2 c_{xx} \right) dt
$$
これは複製ポートフォリオによる資産の変化$dX(t)$の式と等しいはずなので，

\Delta(t) = c_x(t,S(t)) \\
r(X(t) - \Delta(t) S(t) ) = c_t + \dfrac{\sigma^2}{2} S(t)^2 c_{xx}

が成り立ちます．とくに$X(t) = c(t,S(t))$に注意すると，$c(t,x)$の満たすべき微分方程式は以下のようになります．
$$
c_t(t,x) + rx c_x(t,x) + \dfrac{1}{2} \sigma^2 x^2 c_{xx}(t,x) = rc(t,x)
$$
これが有名なブラックショールズ方程式です．伊藤の公式，伊藤ルールさえ知っていれば，かなり自然に導かれることがわかると思います．
なお，偏微分方程式には初期条件と境界条件が必要となります．今回は初期条件の代わりに，終末条件が与えられます．
$$
c(T,S(T)) = (S(T) - K)^+
$$
これはヨーロピアン・コールオプションの定義から理解できます．また，境界条件は以下のようになります．

c(t,0) = 0 \\
\lim_{x \to \infty} [ c(t,x) - (x - e^{-r(T-t)} K) ] = 0

一つ目の式は，価値が$0$の原資産はモデルから価格が常に$0$であり，よってコールオプションに価値がないことを意味しています．また二つ目の式は，原資産の価値が十分大きく行使価額$K$を上回ることが確実なときは後述のフォワード契約と同じになると解釈できます．
なお，ブラックショールズ方程式が原資産の期待収益率$\alpha$に依らないということも重要です．ゆえに，考えるべきパラメータとして測定が非自明なのはボラティリティ$\sigma$だけです．

ブラックショールズ方程式の厳密解とグリークス

一見複雑に見えるブラックショールズ方程式ですが，厳密に解くことができます．また，$c(t,x)$の偏微分には名前がついており，それらも解析的に計算できます．

厳密解

ブラックショールズ方程式の厳密解は以下のように与えられます：
$$
c(t,x) = x \Phi(d_+ (T-t,x))) - K e^{-r(T-t)} \Phi(d_- (T-t,x))
$$
ただし

d_{\pm} (\tau, x) = \dfrac{1}{\sigma \sqrt{\tau}} \left[ \log \dfrac{x}{K} + \left( r\pm \dfrac{1}{2} \sigma^2 \right) \tau \right] \\
\Phi(x) = \dfrac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-x'^2/2} dx'

です．
はじめの話に戻ると，コールオプションの価格を求めることが本題でした．これは
$$
c(0,S(0)) = S(0) \Phi(d_+(T,S(0)) - K e^{-rT} \Phi(d_- (T,S(0)))
$$
で計算できます．ゆえに，プライシングの際にはこの式で十分なわけです．
ではなぜ一般の時刻$t$における価値$c(t,S(t))$をわざわざ求めたのかという疑問が残ります．実は，各時刻におけるオプションの価値を求められるという以上の意味があります．

グリークス

$c(t,x)$の偏微分には名前があり，総してグリークスと呼びます．

• デルタ
  厳密解から頑張って計算すると，$c_x(t,x)$は
  $$
  c_x(t,x) = \Phi(d_+ (T-t,x))
  $$
  と求められ，これをデルタと呼びます．ここで，複製ポートフォリオを構成したときに$\Delta(t) = c_x(t,S(t))$と求められたことに注意します．つまり，複製ポートフォリオのうち原資産をどれだけ持つべきかをデルタが表しているということを意味しているのです．$c(t,x)$を計算することにより，どのように複製ポートフォリオ$\Delta(t)$を構成すべきかがわかるという点が非常に重要です．
  細かいことですが，$\Phi$の定義よりデルタは$0$から$1$の値しか取りません．ここから複製ポートフォリオにおいて，原資産の空売りや銀行での借り入れが必要ないということが読み取れます．

• ガンマ
  同様に計算すると，$c_{xx}(t,x)$は
  $$
  c_{xx}(t,x) = \dfrac{1}{\sigma x \sqrt{T-t}} \Phi'(d_+ (T-t,x))
  $$
  によって求められ，これをガンマと呼びます．明らかに正であることもわかります．ガンマが主役となるポートフォリオの構成については，次回の記事で触れようと思います．

• セータ
  さらに$c_t(t,x)$は
  $$
  c_t(t,x) = -rK e^{-r(T-t)} \Phi(d_- (T-t,x)) - \dfrac{\sigma x}{2 \sqrt{T-t}} \Phi'(d_+ (T-t,x))
  $$

で求められます．明らかですが，セータは負の値しか取りません．つまり，プレミアム$c(t,x)$が時間によって減少するという効果を表します．
上述の厳密解がブラックショールズ方程式を満たすことを確認する最も簡単な方法は，各項にグリークスを代入することでしょう．また終末条件や初期条件を満たすことも確認できますが，それは意外と簡単ではありません(「ファイナンスのための確率解析II」練習問題4.9参照)．

ヨーロピアン・コールオプションの実装

上述の内容を簡単に実装したものが以下です．$d_{\pm}(T-t,x)$が$t \to T$で発散してしまうため，簡単な場合分けをしています．地味にscipy.stats.norm.cdfにinfを代入しても正しい結果を返してくれることに感動しました．get_option_valueが$c(t,S(t))$を求めるメソッドです．

import numpy as np
from scipy.stats import norm 
# parameters
S0 = 100 # initial stock price
K = 105 # strike price
r = 0.05 # interest rate / year
sigma = 0.4 # volatility
T = 1.0 # 1 year

class European_call_option:
    def __init__(self,K,r,sigma,T):
        self.K = K
        self.r = r
        self.sigma = sigma
        self.T = T

    def get_d_list(self,t,S):
        epsilon = 0.0001
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        if t < T - epsilon:
            d_plus = (1.0 / (sigma*np.sqrt(T-t))) * (np.log(S/K) + (r+0.5*sigma*sigma)*(T-t))
            d_minus = (1.0 / (sigma*np.sqrt(T-t))) * (np.log(S/K) + (r-0.5*sigma*sigma)*(T-t))
        elif T-epsilon < t <= T:
            d_plus = np.zeros(S.shape)
            d_minus = np.zeros(S.shape)
            d_plus[S > K] = float("inf")
            d_plus[S < K] = -float("inf")
            d_minus = d_plus
        else:
            print("Error: t shold be smaller than T")
            exit()
        return [d_plus, d_minus]

    def get_option_value(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return S*norm.cdf(d_plus) - K*np.exp(-r*(T-t))*norm.cdf(d_minus)
    def get_delta(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return norm.cdf(d_plus)
    def get_gamma(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return (1.0 / (sigma*S*np.sqrt(T-t))) * norm.pdf(d_plus)
    def get_theta(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return -r*K*np.exp(-r*(T-t))*norm.cdf(d_minus) - (sigma*S) / (2*np.sqrt(T-t)) * norm.pdf(d_plus)
model = European_call_option(K,r,sigma,T)
model.get_option_value(0, S0)

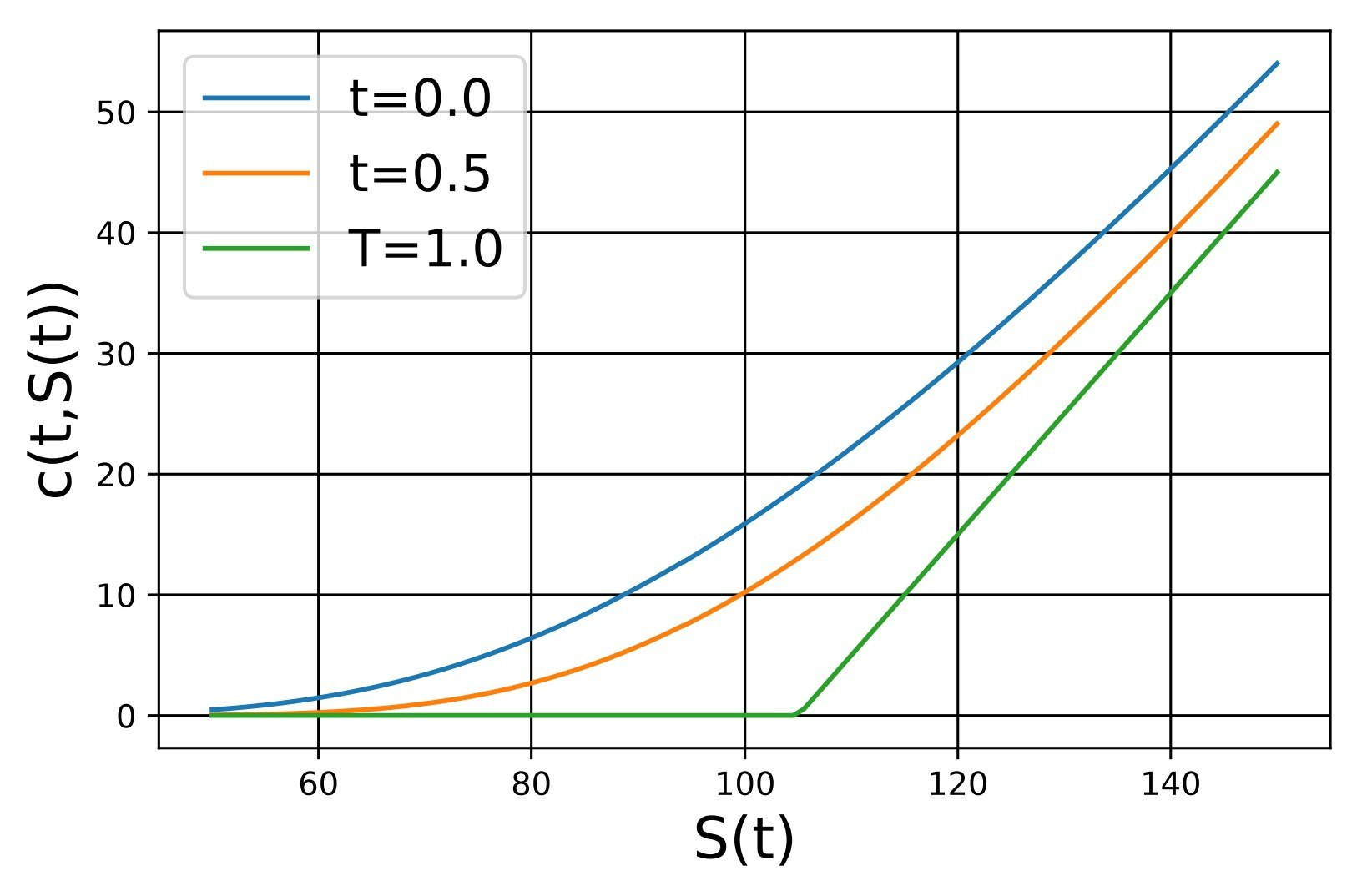
上に示した設定で，$t = 0, 0.5, 1.0$の各時刻において$c(t,S(t))$をグラフに示したものが以下の図です．ヨーロピアン・コールオプションを理解する上では非常に重要になります．例えば，時間が経過するにつれてオプションの価値が目減りしていますが，これは原資産の"伸びしろ"がなくなるため，オプションの時間的価値が減少することを意味します．

(細かい人のための追記)

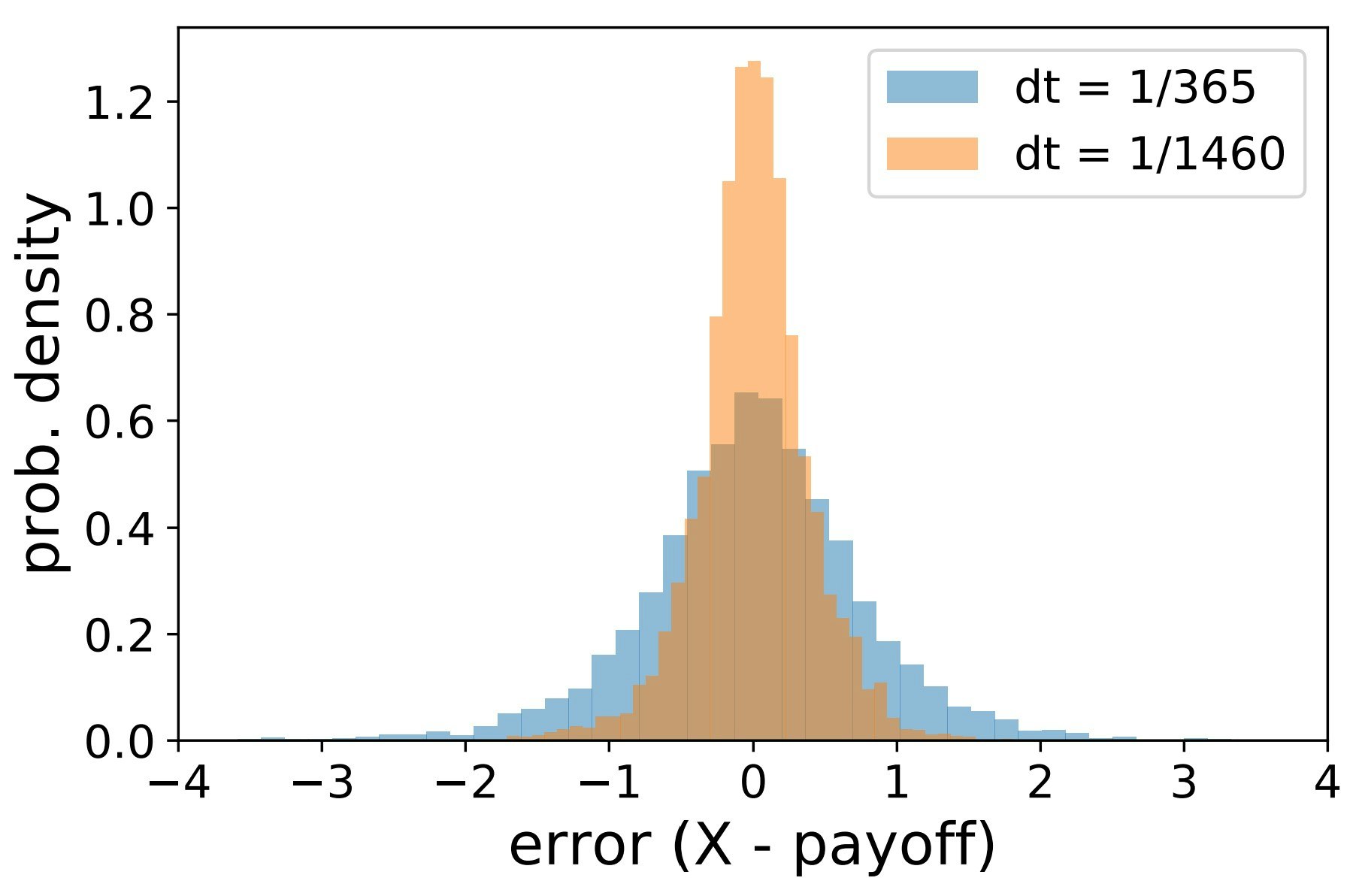
原資産が下がる可能性も低くなるため，オプションの価値が減少することは自明でないと考える人もいるかもしれません．しかし，原資産のモデル化より価格に下限はあるものの上限はないため，やはり満期までの時間が長いことはプレミアムを引き上げる効果を持ちます．これは$c_t(t,x)$が負になることからも分かります．同様に考えると，ボラティリティが大きいときもプレミアムが増加することも理解できます．

そのほかのグリークスの特徴も反映されています．

また計算結果を確認するために，適当に生成した$S(t)$のパスに対して複製ポートフォリオを構成できるかをチェックします．再度，$\Delta(t) = c_x(t,S(T))$に注意します．工夫すれば高速化できるかもしれませんが，面倒なので愚直に実装しました．$X(t)$が複製ポートフォリオになっていれば，時刻$t=T$において$X(T)$と$(S(T)-K)^+$が等しくなっているはずです．ただし，実際に複製ポートフォリオを構成する際は離散的な刻み幅によってポートフォリオを動かす必要があります．今回は満期を$T=1~[\sf year]$とし，$365$回と$365\times 4$回のグリッドで刻みつつ計算しました．

alpha = 0.1 # expected rate of return
time_step = 365
dt = T / days
N = 8000
t_list = np.linspace(0.0, T, time_step)

S_list = np.zeros(N)
X_list = np.zeros(N)

for i in range(N):
    print(i,end = "\r")
    S = S0
    X = model.get_option_value(0.0, S0)
    for t in t_list:
        delta = model.get_delta(t, S)
        S_new = S*(1.0 + alpha*dt + sigma*norm.rvs()*np.sqrt(dt))
        X = X + delta*(S_new - S) + r*(X - delta*S)*dt
        S = S_new
    S_list[i] = S
    X_list[i] = X
payoff_list = (S_list > K)*(S_list - K)
error = X_list - payoff_list

まぁこんな感じじゃないでしょうか．タイムステップを細かく刻むと，エラーが小さくなっていることがわかります．タイムステップとエラーの関係は少し気になりますが，面倒なのでここでは立ち入りません．本当は相対誤差から評価をすべきですが，ペイオフが$0$になってしまいうまく定義ができないので諦めました．

プットオプション・フォワード契約

オプション取引には，コールオプション以外にも様々なものがあります．ここではプットオプションとフォワード契約について述べ，それらの間に成り立つ関係式を示します．

プットオプション・フォワード契約の定義

コールオプション同様のオプション契約として，ヨーロピアン・プットオプションを定義します．ヨーロピアン・プットオプションを購入するとは，「時刻$t=T$において，原資産の価格$S(T)$によらず，行使価額$K$で原資産を1単位売却できる"権利"を購入する」ということです．
コールオプションと同様に考えると，時刻$t = T$におけるヨーロピアン・プットオプションの"価値"は以下のようになります：
$$
(K - S(T))^+
$$

さらに，フォワード契約を以下のように定義します．フォワード契約を保有するとは，「時刻$t=T$において，原資産の価格$S(T)$によらず，行使価額$K$で原資産を1単位購入する"義務"を負う」ということです．よって，時刻$t=T$におけるフォワード契約の"価値"は
$$
S(T) - K
$$
です．
フォワード契約の複製ポートフォリオは以下のように構成できます．$t=0$において原資産を1単位購入し取引をしないようなポートフォリオを考えると，
$$
X(t) = S(t) + e^{rt} (X(0) - S(0))
$$
がこのポートフォリオの価値となります．よって，時刻$T$におけるキャッシュフローを再現するという条件から，$S(T) - K = X(T)$が成り立ちます．以上から，
$$
X(0) = S(0) - K e^{-rT}
$$
が得られ，
$$
X(t) = S(t) - K e^{-r(T-t)}
$$
が複製ポートフォリオの価値，すなわちフォワード契約の価値になります．

プット-コール・パリティ

時刻$t$において原資産価格が$S(t)$であるときのコールオプションの価値を$c(t,S(t))$
，プットオプションの価値を$p(t,S(t))$，フォワード契約の価値を$f(t,S(t))$とします．
一般に，以下の式が成り立つことに注意します：
$$
x - K = (x - K)^{+} - (K-x)^{+}
$$
これは丁寧に場合分けすると直ちにわかります．時刻$T$におけるオプションの価値が$c(T,S(T)) = (S(T)-K)^+$，$p(T,S(T)) = (K-S(T))^+$，$f(T,S(T)) = S(T) - K$で与えられたことを思い出すと，
$$
f(T,S(T)) = c(T,S(T)) - p(T,S(T))
$$
が得られます．
いま$t < T$において，$f(t,S(t)) > c(t,S(t)) - p(t,S(t))$であったとします．前述のように，それぞれのオプションに対応する複製ポートフォリオを構成することができることに注意すると，コールオプションを買い，フォワード契約とプットオプションを売るという操作が可能になります．ゆえに，$f(t,S(t)) + p(t,S(t)) - c(t,S(t)) > 0$という利益が即座に得られます．このポジションは時刻$t=T$において$c(T,S(T)) - f(T,S(T)) + p(T,S(T)) = 0$となるため，手元資金$0$から始めて確実に利益が得られる裁定機会が生じていることになります．裁定が生じないように価格を決めたいため，はじめの不等号は成り立ちません．また逆向きの不等号が成り立つとしても，やはり裁定機会が生じます．以上から，不等号ではなく等号でなければならないということがわかります：
$$
f(t,S(t)) = c(t,S(t)) - p(t,S(t))
$$
オプション価値に関するこの関係式を，プット-コール・パリティと呼びます．特に重要なのは，$dS(t)$のモデル化に言及することなく導出されたということです．つまり，原資産がいかなるダイナミクスに従っていようと，プット-コール・パリティは成立します．

プット・オプションの従う方程式

コール・オプションの価値$c(t,S(t))$の満たすべきブラックショールズ方程式
$$
c_t(t,x) + rx c_x(t,x) + \dfrac{1}{2} \sigma^2 x^2 c_{xx}(t,x) = rc(t,x)
$$
は，コール・オプションの定義を使うことなく導出されたことに注意します．コール・オプションの定義は終末条件(および境界条件)のみでしか使われていません．
よって，プット・オプションの価値$p(t,S(t))$も全く同じ式を満たします：
$$
p_t(t,x) + rx p_x(t,x) + \dfrac{1}{2} \sigma^2 x^2 p_{xx}(t,x) = rp(t,x)
$$
さらに，複製ポートフォリオは
$$
\Delta(t) = p_x(t,S(t))
$$
によって構成されることも全く同様にわかります．
さらに，プット・オプションのグリークスもプット-コール・パリティを用いると簡単に求められます：

p_x(t,x) = -\Phi(-d_{+}(T-t,x))  < 0 \\
p_{xx}(t,x) = \dfrac{1}{\sigma x \sqrt{T-t}} \Phi'(d_+ (T-t,x)) > 0 \\
p_t(t,x) = rK e^{-r(T-t)} \Phi(-d_- (T-t,x)) - \dfrac{\sigma x}{2 \sqrt{T-t}} \Phi'(-d_+ (T-t,x))

特に，デルタ$\Delta(t) = p_x(t,S(t)) < 0$であることは，原資産を常に空売りする必要があることを意味しています．

ヨーロピアン・プットオプションの実装と計算例を示します．

# parameters
S0 = 100 # initial stock price
K = 105 # strike price
r = 0.05 # interest rate / year
sigma = 0.4 # volatility
T = 1.0 # 1 year

class European_put_option:
    def __init__(self,K,r,sigma,T):
        self.K = K
        self.r = r
        self.sigma = sigma
        self.T = T

    def get_d_list(self,t,S):
        epsilon = 0.0001
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        if t < T - epsilon:
            d_plus = (1.0 / (sigma*np.sqrt(T-t))) * (np.log(S/K) + (r+0.5*sigma*sigma)*(T-t))
            d_minus = (1.0 / (sigma*np.sqrt(T-t))) * (np.log(S/K) + (r-0.5*sigma*sigma)*(T-t))
        elif T-epsilon < t <= T:
            d_plus = np.zeros(S.shape)
            d_minus = np.zeros(S.shape)
            d_plus[S > K] = float("inf")
            d_plus[S < K] = -float("inf")
            d_minus = d_plus
        else:
            print("Error: t shold be smaller than T")
            exit()
        return [d_plus, d_minus]

    def get_option_value(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return S*(norm.cdf(d_plus)-1.0) - K*np.exp(-r*(T-t))*(norm.cdf(d_minus)-1.0)
    def get_delta(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return norm.cdf(d_plus) - 1.0
    def get_gamma(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return (1.0 / (sigma*S*np.sqrt(T-t))) * norm.pdf(d_plus)
    def get_theta(self,t,S):
        K, r, sigma, T = self.K, self.r, self.sigma, self.T
        d_plus, d_minus = self.get_d_list(t,S)
        return -r*K*np.exp(-r*(T-t))*(norm.cdf(d_minus)-1.0) - (sigma*S) / (2*np.sqrt(T-t)) * norm.pdf(d_plus)
model = European_put_option(K,r,sigma,T)
model.get_option_value(0, S0)

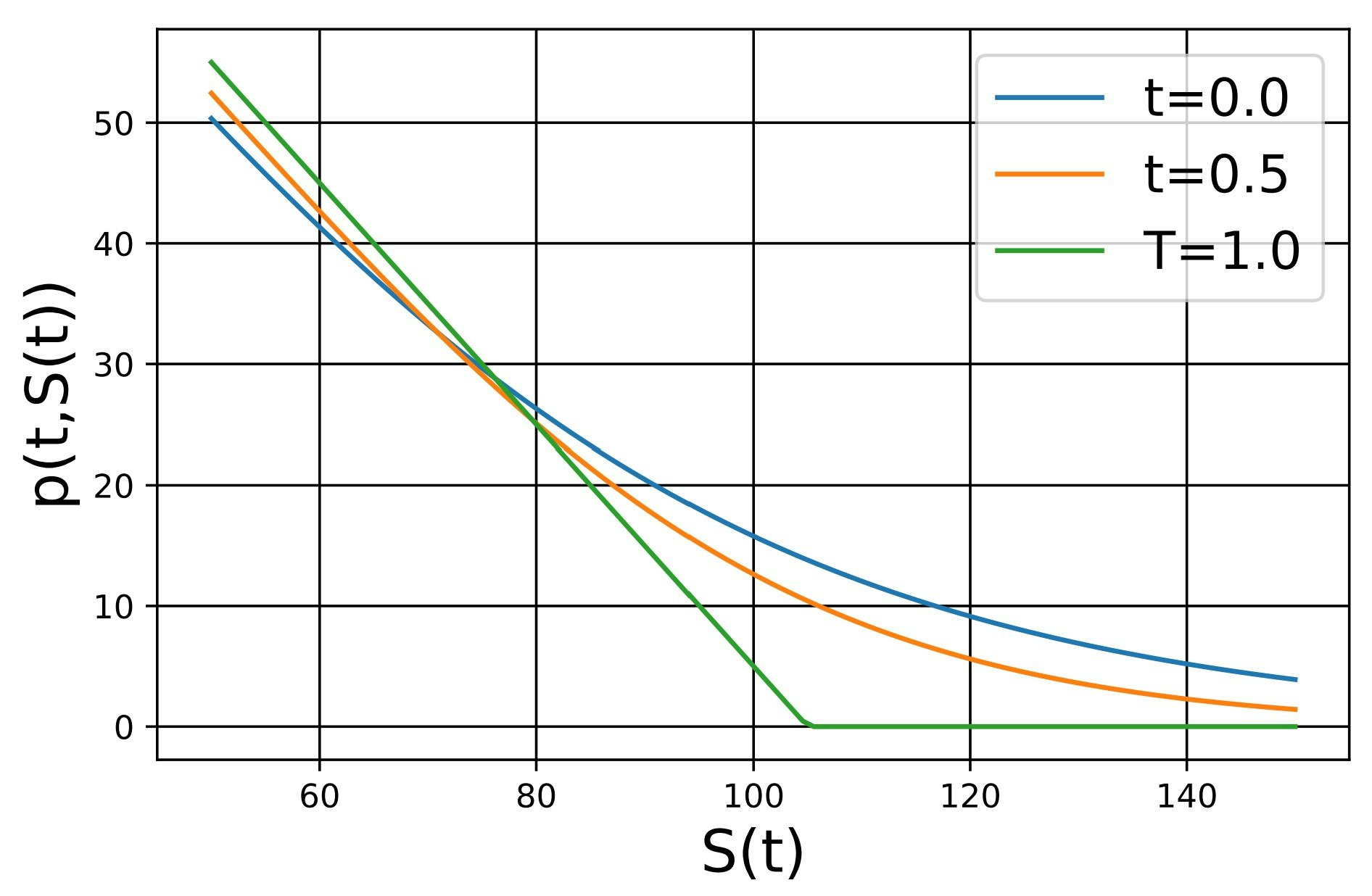
コール・オプションとの比較で特に注意すべき点は，$S(t)$が小さいときプレミアムが時刻$t=T$におけるキャッシュフロー$(K-S(T))^+$を下回っているということです．これは，$S(0) = 0$という極端な場合を考えると理解しやすいでしょう．原資産のモデルから$S(t) = 0$が導かれるため，プット・オプションにより必ず行使価額$K$が手に入ります．つまり，プット・オプションは「時刻$t=T$において確実に$K$なる金額を手に入れる権利」になるわけです．これは，時刻$t=0$において$K e^{-rT}$だけ預金して，時刻$t=T$に引き出すこととまったく等価であり，複製ポートフォリオになっています．よって，初期資産$X(0) = K e^{-rT}$だけあればキャッシュフローを再現できることから，$S(0) = 0$のときのプット・オプションは$K e^{-rT} (< K)$となり，プット・オプションの時間的価値が負であることがわかります．将来のキャッシュフローをこのように金利でディスカウントすることも，複製ポートフォリオの考え方から統一的に理解できます．

まとめ

複製ポートフォリオの考え方に基づき，ヨーロピアン・コールオプションの価値$c(t,S(t))$を求めるブラックショールズ方程式とその厳密解を導きました．またグリークスとその意味についても述べ，pythonによる実装を与えました．
さらにヨーロピアン・プットオプションとフォワード契約を定義し，これらの間の関係であるプット-コール・パリティを示しました．またプットオプションの厳密解およびグリークスも計算し，実装をしました．

ここではヨーロピアンタイプのオプションのみを扱いましたが，アメリカンタイプ(満期時でなくても権利を行使できる)，バミューダタイプ(ヨーロピアンとアメリカンの中間)など様々なものがあります．また$t=T$における原資産価格$S(T)$のみでペイオフが決まるコール・プット以外にも，$S(t)$の平均値でペイオフが決まるアベレージオプション(アジアンオプション)，$S(t)$の最大値でペイオフが決まるルックバックオプションなどがあります．
このような複雑なオプションは，オプション価値の厳密解が求められるわけではないことが多いです．そのため，モンテカルロ法や二項ツリーモデルなど様々な数値計算手法により取り組む必要があります．