分配関数をsum-productアルゴリズムで計算する

「パターン認識と機械学習」を読んでいて，8章のsum-productアルゴリズムを実装しようと思いました．ただ，具体的なベイジアンネットワークの例はすぐに思いつかず，統計力学に頼ることにしました．いろいろ調べていると統計力学でおなじみの分配関数が厳密に計算できたり，基底状態(組み合わせ最適化問題としては大域最適解)を求められたりで非常に関係が深いようです．ここを深堀りすると非常に面白いとは思いますが，力量不足ゆえ簡単な例と実装を示すだけにとどめます．
なお，記法は「パターン認識と機械学習」に合わせています．

設定

今回はツリー状のネットワークに配置されたスピン$x_i = \pm 1$が相互作用を持つ系を考えます：
$$
H = -\sum_{(i,j)} J_{ij} x_i x_j
$$
ただし$J_{ij}$は確率的に決まるものとし，この意味でスピングラス系を扱っていると言えます．
このとき，系がカノニカル分布に従うと仮定すると確率分布は
$$
p({\bf x}) = \dfrac{1}{Z(\beta)} \exp [-\beta H]
$$
によって与えられます．この確率分布をグラフィカルモデルに置き換えるために$\psi_{ij}(x_i,x_j) = \exp [\beta J_{ij} x_i x_j ]$を定義すると
$$
p({\bf x}) = \dfrac{1}{Z(\beta)} \prod_{(ij)} \psi_{ij}(x_i,x_j)
$$
のように変形できるため，スピンのネットワークをそのままグラフィカルモデルに置き換えた無向グラフが得られます．よってfactorノードは
$$
f_{ij}(x_i,x_j) = \psi_{ij}(x_i,x_j) = \exp [\beta J_{ij} x_i x_j ]
$$
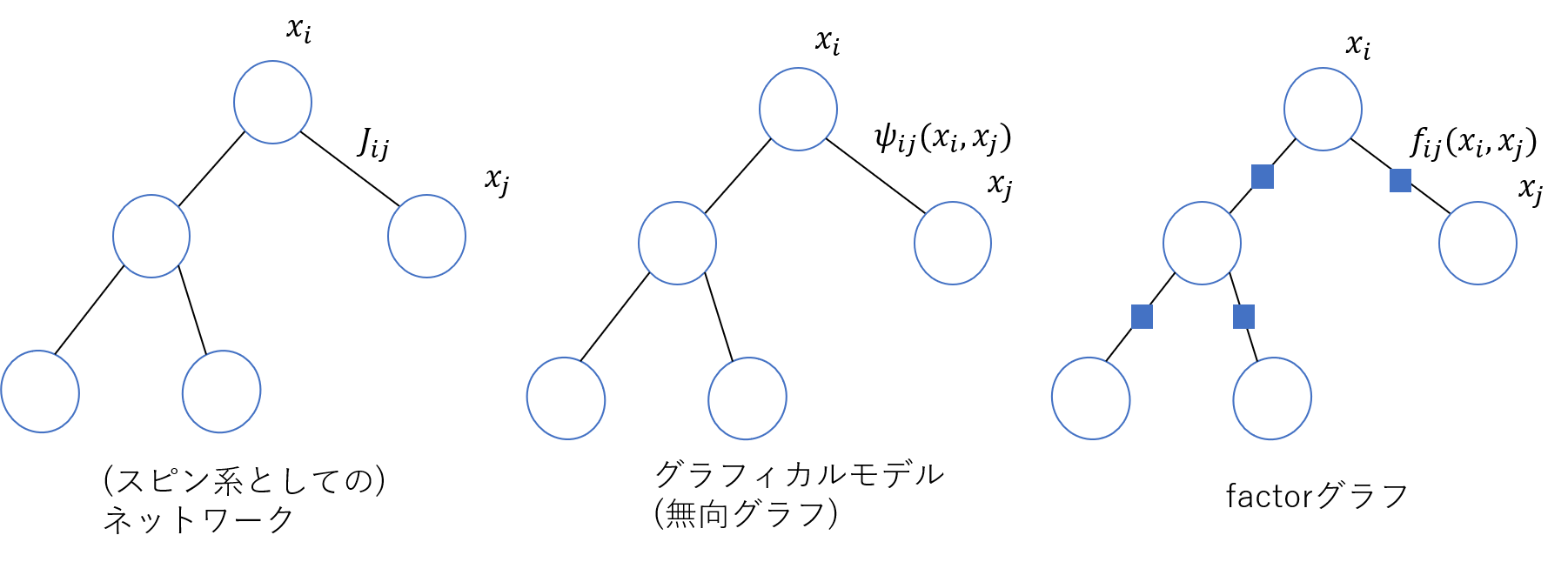
となるため，factorノードは枝が張られている$(i,j)$の間に挿入すればよいこともわかります．このようにして得られるfactorグラフは自明にツリー状ですので，sum-productやmax-sumアルゴリズムを実行することができます．以下では変数ノードを〇で，factorノードを□で表すことにします．
以下の図に，それぞれのネットワークの関係を示します．

まずはこのようなネットワークの生成などのためのコードを示します．詳細は省きます．

import numpy as np

class tree: # 適当なツリーを生成する
    def __init__(self, N):
        self.edges = []
        self.children_of = [[] for _ in range(N)] # childrenは複数
        self.parent_of = [[] for _ in range(N)] # parentは一意
        self.leaves = [0] # 0をrootとする

        for n in range(1,N):
            if n == 1: # node nをくっつけるnode iを決める
                i = 0
            else:
                i = np.random.choice(n-1)

            self.edges.append([i,n])
            self.leaves.append(n)
            if i in self.leaves:
                self.leaves.remove(i)

            self.children_of[i].append(n)
            self.parent_of[n] = i

N = 10 # N=10くらいでチェックするとうまくできていたため大丈夫そう
network = tree(N)
print(network.edges)
print(network.leaves)

# Jの生成やfの定義
J = {}
for edge in network.edges:
    i, j = edge
    J[str(i)+","+str(j)] = np.random.normal()

def f(beta, J_ij, x_i, x_j):
    return np.exp(beta*J_ij*x_i*x_j)
print(J)

sum-productアルゴリズムによる分配関数の計算

まずsum-productアルゴリズムについて簡単に触れ，それを用いた分配関数の計算を述べます．最後に実装を示します．

sum-productアルゴリズム

前述の$f_{ij}(x_i,x_j)$を用いると，確率分布は
$$
p({\bf x}) = \dfrac{1}{Z(\beta)} \prod_{(ij)} f_{ij} (x_i,x_j)
$$
によって表現できることに注意します．また，規格化定数(分配関数)を除いた
$$
\tilde{p}({\bf x}) = \prod_{(ij)} f_{ij} (x_i,x_j)
$$
を定義します．

sum-productアルゴリズムはあるノード$x_n$に対する周辺分布$p(x_n)$を求めるものです．具体的には，以下のような手続きを踏みます：

(1) あるノード$x_n$を選び，ルートとする．
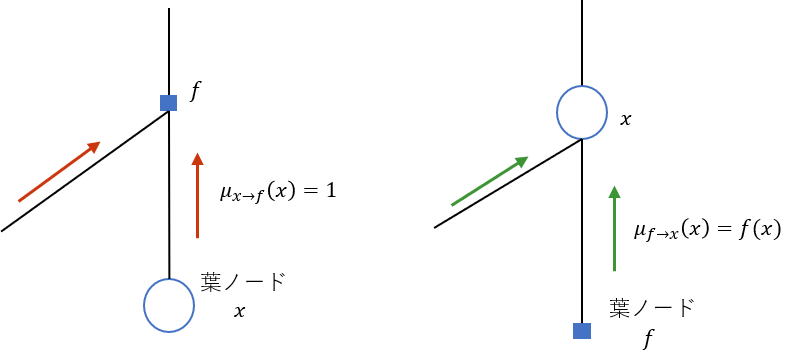
(2) ルートに対する葉ノードをすべて探し，それが変数ノード(〇)であるときはfactorノード(□)に対しメッセージ$\mu_{x \to f}(x) = 1$を伝播させる．逆にfactorノード(□)であるときは変数ノード(〇)に対しメッセージ$\mu_{f \to x}(x) = f(x)$を伝播させる．

(3) 葉ノードから順に，ルートに向けて以下の式に基づいてメッセージを伝播させる．ただし，$N(x)$や$N(f)$はそれぞれ変数ノード$x$とfactorノード$f$の隣接ノードを表す．

\mu_{x \to f}(x) = \prod_{l \in N(x) \setminus f} \mu_{f_l \to x}(x)\\
\mu_{f \to x}(x) = \sum_{x_1, \cdots, x_M} f(x,x_1,\cdots,x_M) \prod_{m \in N(f) \setminus x} \mu_{x_m \to f}(x_m)

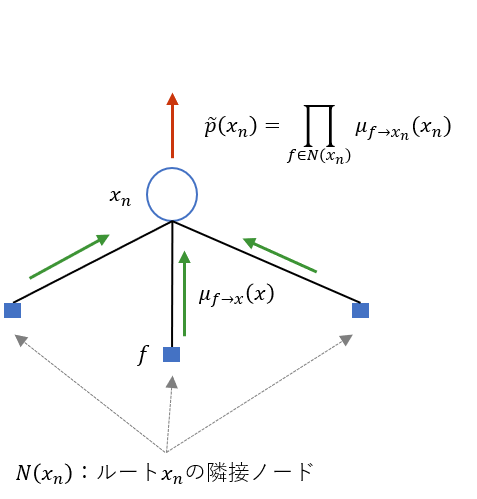
(4) ルート$x_n$において，$\prod_{f \in N(x_n)} \mu_{f \to x_n}(x_n)$を計算すると，これは$\tilde{p}({\bf x})$を周辺化した$\tilde{p}(x_n)$となる．つまり
$$
\tilde{p}(x_n) = \prod_{f \in N(x_n)} \mu_{f \to x_n}(x_n)
$$
である．これは(3)が本質的には各factorノードについて$f$をかけ，各変数ノードについて$\sum_x$をとるという操作しかしていないことから理解できるが，きちんと示すには頑張る必要がある．

(5) 明らかに$\sum_{x_n} \tilde{p}(x_n) = Z(\beta) \sum_{x_n} p(x_n) = Z(\beta)$だから，規格化定数が計算できる．よって，$p(x_n) = \dfrac{1}{Z(\beta)} \tilde{p}(x_n)$が計算できた．

以上がsum-productアルゴリズムです．

分配関数の計算

前述のsum-productアルゴリズムから，規格化定数(分配関数)$Z(\beta)$が
$$
Z(\beta) = \sum_{x_n} \tilde{p}(x_n)
$$
によって求められることがわかります．よって，ツリー状のネットワークに配置されたスピン系に対して，sum-productアルゴリズムを用いることで分配関数が計算できます．
一般には分配関数の計算には指数オーダーの計算量が必要であったことを思い出すと，計算量が大幅に削減できていることがわかります．
なお，このような計算が可能なのは明らかにネットワークがツリー状であるためです．一般にループを持つような場合にはこの手法は適用できません．一方で，ネットワークの構造によっては無理やりsum-productを適用することである程度良い結果が得られることもあるそうです．詳しくはloopy belief propagationで調べてみてください．

Pythonによる実装

今回の問題に対して，sum-productアルゴリズムをPythonで実装してみました．上述のアルゴリズムを見ても分かるように，(ツリー状であったとしても)一般のネットワークに対しては実装は簡単ではありません．しかし今回の設定では，factorノードは2つのスピン変数としか隣接しないため，かなり単純化することができます．メッセージ$\mu$をどのように管理するかが実装の肝ですが，辞書型で無理やり扱うことにしました．アルゴリズムの流れとしては，ネットワークを生成する際に発見した葉ノードから始めて，ルートに近づきつつ葉ノードを入れ替えるような形になっています．

import copy

spin = [1.0, -1.0]

beta = 1.0
beta_start = 0.1
beta_end = 4.0
beta_list = np.linspace(beta_start, beta_end, 100) # いくつかのbetaの値に対し分配関数を計算する
Z_list = np.ones(100)

for s,beta in enumerate(beta_list):
    mu_x_to_f = {} # 可読性のために辞書型で管理
    mu_f_to_x = {}
    leaves = copy.deepcopy(network.leaves) # こうしないとnetwork.leavesが置き換わってしまう
    children_of = copy.deepcopy(network.children_of)

    while leaves != [0]: # leavesからrootまでたどる．
        i = leaves.pop(0) # leavesの一つを取り出す
        j = network.parent_of[i] # そのparent(一意)を見つける
        #print(i,j)
        direction = str(i)+"->"+str(j) # 辞書のkey
        interaction = str(j)+","+str(i)
        mu_x_to_f[direction] = np.ones(2) # 初期化条件
        for k in network.children_of[i]:
            #print("yey")
            direction_previous = str(k)+"->"+str(i)
            mu_x_to_f[direction] *= mu_f_to_x[direction_previous]

        # 可読性のために回りくどく書いたら逆にわかりにくくなった説
        mu_f_to_x[direction] = np.zeros(2)
        mu_f_to_x[direction][0] = f(beta,J[interaction],spin[0],spin[0])*mu_x_to_f[direction][0] + f(beta,J[interaction],spin[0],spin[1])*mu_x_to_f[direction][1]
        mu_f_to_x[direction][1] = f(beta,J[interaction],spin[1],spin[0])*mu_x_to_f[direction][0] + f(beta,J[interaction],spin[1],spin[1])*mu_x_to_f[direction][1]
        #print(mu_f_to_x[direction])

        children_of[j].remove(i) # jをleavesにしていいか判定するため，iを子ノードから除く
        if len(children_of[j]) == 0: # 子ノードがいなければleavesに加える
            leaves.append(j)
        #print(leaves)

    p0 = np.ones(2) # p(x_0)をベクトルとして表記
    for i in network.children_of[0]:
        direction = str(i)+"->"+str(0)
        p0 *= mu_f_to_x[direction]
    Z_list[s] = sum(p0)

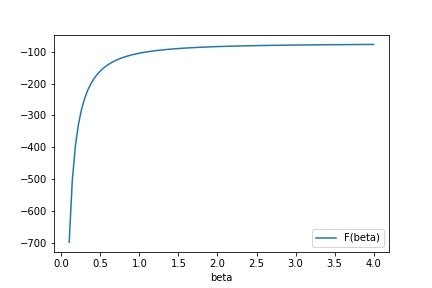
分配関数$Z(\beta)$が求まったので，自由エネルギー$F(\beta) = -\dfrac{1}{\beta} \log Z(\beta)$が計算できます．実際にやってみると，以下のようになりました．

max-sumアルゴリズムによる基底状態の計算

まずmax-sumアルゴリズムについて簡単に述べ，それを用いた基底状態の計算を説明します．最後に実装を示し，確かにエネルギー最小の状態が得られていることを確認します．

max-sumアルゴリズム

max-sumアルゴリズムは，sum-prodoctアルゴリズムにおける$\sum$を$\max$に，$\prod$を$\sum$に置き換えることにより得られるアルゴリズムで，$p({\bf x})$の最大値および最大値を与える${\bf x} ^ { * }$が求められます．手続きはsum-productアルゴリズムとほとんど同様ですが，${\bf x} ^ { * }$を計算するためにルートからの逆伝播などが必要になります．

(1) あるノード$x_n$を選び，ルートとする．
(2) ルートに対する葉ノードをすべて探し，それが変数ノード(〇)であるときはfactorノード(□)に対しメッセージ$\mu_{x \to f}(x) = 0$を伝播させる．逆にfactorノード(□)であるときは変数ノード(〇)に対しメッセージ$\mu_{f \to x}(x) = \log f(x)$を伝播させる．

(3) 葉ノードから順に，ルートに向けて以下の式に基づいてメッセージを伝播させる．ただし，$N(x)$や$N(f)$はそれぞれ変数ノード$x$とfactorノード$f$の隣接ノードを表す．

\mu_{x \to f}(x) = \sum_{l \in N(x) \setminus f} \mu_{f_l \to x}(x)\\
\mu_{f \to x}(x) = \max_{x_1, \cdots, x_M} \left[ \log f(x,x_1,\cdots,x_M) +\sum_{m \in N(f) \setminus x} \mu_{x_m \to f}(x_m) \right]

その際，各$x$に対し
$$
{\bf \phi} _ f (x) = \arg \max_{x_1,\cdots,x_M} \left[ \log f(x,x_1,\cdots,x_M) +\sum_{m \in N(f) \setminus x} \mu_{x_m \to f}(x_m) \right]
$$
を保存しておく．これは(5)における逆伝播で必要となる．

(4) ルート$x_n$において，
$$
p_{\rm max} = \max_{x_n} \left[ \sum_{f \in N(x_n)} \mu_{f \to x_n} (x_n) \right]
$$
を計算すると，これが$p({\bf x})$の最大値となる．また，$x ^ { * } _ n$は
$$
x ^ { * } _ n = \arg \max_{x_n} \left[ \sum_{f \in N(x_n)} \mu_{f \to x_n} (x_n) \right]
$$
によって求められる．

(5) ルート$x_n$から逆伝播を行い，
$$
(x ^ * _1, \cdots, x ^ * _M) = {\bf \phi} _ f (x)
$$
のようにして${\bf x} ^ { * }$を求める．

以上がmax-sumアルゴリズムの手続きです．

基底状態の計算

カノニカル分布
$$
p({\bf x}) = \dfrac{1}{Z(\beta)} \exp [-\beta H]
$$
から明らかなように，$p({\bf x})$の最大値を与える${\bf x} ^ { * }$はハミルトニアンの最小値を与えます．つまり，max-sumアルゴリズムにより${\bf x} ^ { * }$を求めることにより，ネットワークにおけるスピン系の基底状態がわかります．なお，ハミルトニアンを損失関数と読み替えると，これは組み合わせ最適化問題を解くことにつながります．max-sumアルゴリズムの手続きをよく見るとわかるように，これは動的計画法そのものです．
統計力学的な目線では，ループが存在するとmax-sumアルゴリズムがうまく適用できないことはフラストレーションの存在として解釈することもできます．グラフ理論や最適化問題，統計力学の密接なつながりを理解できる，非常に興味深い例だと思います．

Pythonによる実装

今回の問題に対して，max-sumアルゴリズムをPythonで実装してみました．ほとんどsum-productアルゴリズムと同様ですが，$\beta = 1$としています．これで一般性を失わないことは，$\log f_{ij}(x_i,x_j) = \beta J_{ij} x_i x_j$となることなどを考えると自明です．

mu_x_to_f = {} # 可読性のために辞書型で管理
mu_f_to_x = {}
phi = {}
leaves = copy.deepcopy(network.leaves) # こうしないとnetwork.leavesが置き換わってしまう
children_of = copy.deepcopy(network.children_of)

spin = [1.0, -1.0]

while leaves != [0]: # leavesからrootまでたどる．
    i = leaves.pop(0) # leavesの一つを取り出す
    j = network.parent_of[i] # そのparent(一意)を見つける
    #print(i,j)
    direction = str(i)+"->"+str(j) # 辞書のkey
    interaction = str(j)+","+str(i)
    mu_x_to_f[direction] = np.zeros(2) # 初期化条件
    for k in network.children_of[i]:
        #print("yey")
        direction_previous = str(k)+"->"+str(i)
        mu_x_to_f[direction] += mu_f_to_x[direction_previous]

    # 可読性のために回りくどく書いたら逆にわかりにくくなった説
    mu_f_to_x[direction] = np.zeros(2)
    mu_f_to_x[direction][0] = max(J[interaction]*spin[0]*spin[0]+mu_x_to_f[direction][0],J[interaction]*spin[0]*spin[1]+mu_x_to_f[direction][1])
    mu_f_to_x[direction][1] = max(J[interaction]*spin[1]*spin[0]+mu_x_to_f[direction][0],J[interaction]*spin[1]*spin[1]+mu_x_to_f[direction][1])
    phi[direction] = np.array([1,1])
    phi[direction][0] = np.argmax([J[interaction]*spin[0]*spin[0]+mu_x_to_f[direction][0],J[interaction]*spin[0]*spin[1]+mu_x_to_f[direction][1]])
    phi[direction][1] = np.argmax([J[interaction]*spin[1]*spin[0]+mu_x_to_f[direction][0],J[interaction]*spin[1]*spin[1]+mu_x_to_f[direction][1]])

    #print(mu_f_to_x[direction])

    children_of[j].remove(i) # jをleavesにしていいか判定するため，iを子ノードから除く
    if len(children_of[j]) == 0: # 子ノードがいなければleavesに加える
        leaves.append(j)

nodes = copy.deepcopy(network.children_of[0]) # こうしないとnetwork.leavesが置き換わってしまう
children_of = copy.deepcopy(network.children_of)

x_optimal = [[] for _ in range(N)]

p_max = np.zeros(2)
for i in network.children_of[0]:
    direction = str(i)+"->"+str(0)
    p_max += mu_f_to_x[direction]   
x_optimal[0] = np.argmax(p_max)

while len(nodes) != 0:
    i = nodes.pop(0)
    j = network.parent_of[i]
    direction = str(i)+"->"+str(j)
    x_optimal[i] = phi[direction][x_optimal[j]]
    nodes.extend(network.children_of[i])

print(x_optimal)
def energy(x):
    E = 0.0
    for edge in network.edges:
        i,j = edge
        E += -J[str(i)+","+str(j)]*spin[x[i]]*spin[x[j]]
    return E
print(energy(x_optimal))
energy_optimal = energy(x_optimal)

チェックのために$10000$個程度のサンプルを生成しエネルギーを比較してみましたが，このアルゴリズムで得られる${\bf x} ^ *$が確かにエネルギーの最小値を与えていました．

まとめ

前半ではsum-productアルゴリズムを用いることで，ツリー状のネットワーク上のスピン系の分配関数を計算しました．また後半ではmax-sumアルゴリズムにより，この系の基底状態を計算しました．この例を通じて，グラフ理論や最適化問題と統計力学の関係の一面を見ることができました．今回の例は単純すぎた部分もあるので，スピンの取る状態を増やしたり，相互作用として三体を含めるなど，様々な拡張をしても面白いかもしれません．