最小二乗法は,実測値$y_i$との「二乗誤差」が最小となるような予測値$\hat{y}_i$を決める方法です.ここで,上記を一般化した「$n$乗誤差」を目的関数とする最小$n$乗法を考えます:
$$
L = \dfrac{1}{N} \sum_i |y_i - \hat{y}_i | ^ n
$$
本記事では,最小$n$乗法による予測値$\hat{y}_i$が持つ性質を議論し,Pythonによる実装を示します.なお元ネタはPRMLのExercise 1.27です.
本記事のサマリー
結論ですが,最小$n$乗法による(関数形に制限がない場合の)予測値$\hat{y}(\bf x)$は以下のようになります.
- $n \to 0$の場合,条件付き最頻値:$\hat{y}(\bf x) = {\rm mode}[y \mid {\bf x}]$
- $n = 1$の場合,条件付き中央値:$\hat{y}(\bf x) = {\rm median}[y \mid {\bf x}]$
- $n = 2$の場合,条件付き期待値:$\hat{y}(\bf x) = {\mathbb E}[y \mid {\bf x}]$
※$n \to 0$に関して数学的に怪しい議論をしており,どのような条件で正当化できるかは不明です
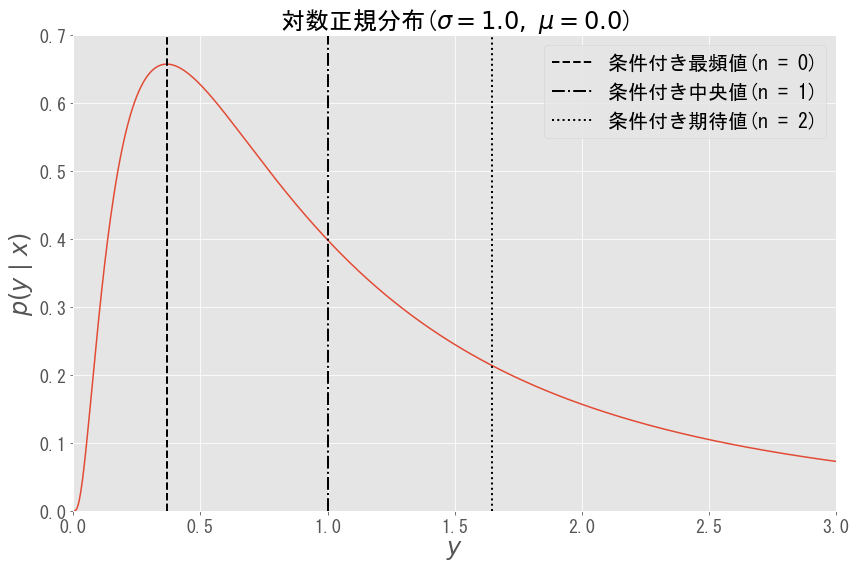
具体例として,出力$y$が以下の対数正規分布($\sigma = 1$,$ \mu = 0 $)に従う場合を想定します.
$$
p(y \mid {\bf x}) = \dfrac{1}{\sqrt{2 \pi} \sigma y} \exp \left[ - \dfrac{(\log y - \mu)^2 }{2 \sigma^2} \right]
$$このとき,最小$n$乗法による予測値$\hat{y}({\bf x})$は$n$の値ごとに下図のようになります.後述しますが,外れ値等の影響で分布が非対称であるとみなる場合,$n$が大きくなるほど予測値$\hat{y}(\bf x)$が大きな$y$の値に引っ張られることとなります.
理論的な背景
まず最小$n$乗法を定式化し,$n$乗誤差について直観的な理解を与えます.その後,いくつかの$n$に対して,最小$n$乗法による予測値$\hat{y}_i$の性質を議論します.
問題設定
$N$個の入力$({\bf x}_1, \cdots, {\bf x}_N)$に対し,出力の実測値$y_i$を$\hat{y}_i = \hat{y}({\bf x}_i)$で予測します.$N$が十分大きいものとすると,$n$乗誤差$L$は以下に収束すると考えてよいでしょう.
$$
L = \dfrac{1}{N} \sum_i |y_i - \hat{y}_i | ^ n \to \int p({\bf x}, y) |y - \hat{y}({\bf x}) | ^ n d{\bf x} dy
$$
ここで$L$の収束先は予測値$\hat{y}({\bf x})$の汎関数であり,以下のように変形できます.
$$
L[\hat{y}] = \int p({\bf x}, y) |y - \hat{y}({\bf x}) | ^ n d{\bf x} dy
= \int p(y \mid {\bf x}) |y - \hat{y}({\bf x}) | ^ n dy~ p({\bf x}) d{\bf x}
$$
変分法を思い出すと,汎関数$L[\hat{y}]$を最小化する$ y ^ * ({\bf x})$は以下を満たします.
$$
\left. \dfrac{\delta}{\delta \hat{y}}\int p(y \mid {\bf x}) |y - \hat{y}({\bf x}) | ^ n dy \right| _ {\hat{y} = y ^ *} = 0
$$
なお,実際には予測値$\hat{y}({\bf x})$の関数形には制限があり,特定の集合$F$に含まれるものに限定されます(例えば線形回帰の場合,重みベクトル${\bf w}$に対して$\hat{y}({\bf x}) = {\bf w}^t {\bf x}$となります).その場合にはLagrange法で変分問題を解くこととなるかと思いますが,ここでは関数形に制限を設けず(あるいは最適な関数$y ^ *$を含むほどに$F$が広いと仮定し),$y ^ * ({\bf x})$の持つ性質を議論します.
直観的な理解
まず$n$乗誤差の特徴から,$n$ごとの予測値$\hat{y}({\bf x})$の性質を考察します.
- $n \to 0$の場合,誤差が$0$に近い領域において$n$乗誤差は$0$,そうでない領域では$1$となります.誤差の「大きさ」は重要でないため,確率密度が高い領域を当てることを優先した予測値となるでしょう.
- $n$が大きくなると,大きい誤差に対してより大きなペナルティーが課されます.例えばデータが外れ値を含んでいる場合,誤差を小さくするため,外れ値に引っ張られた予測をする可能性があります.
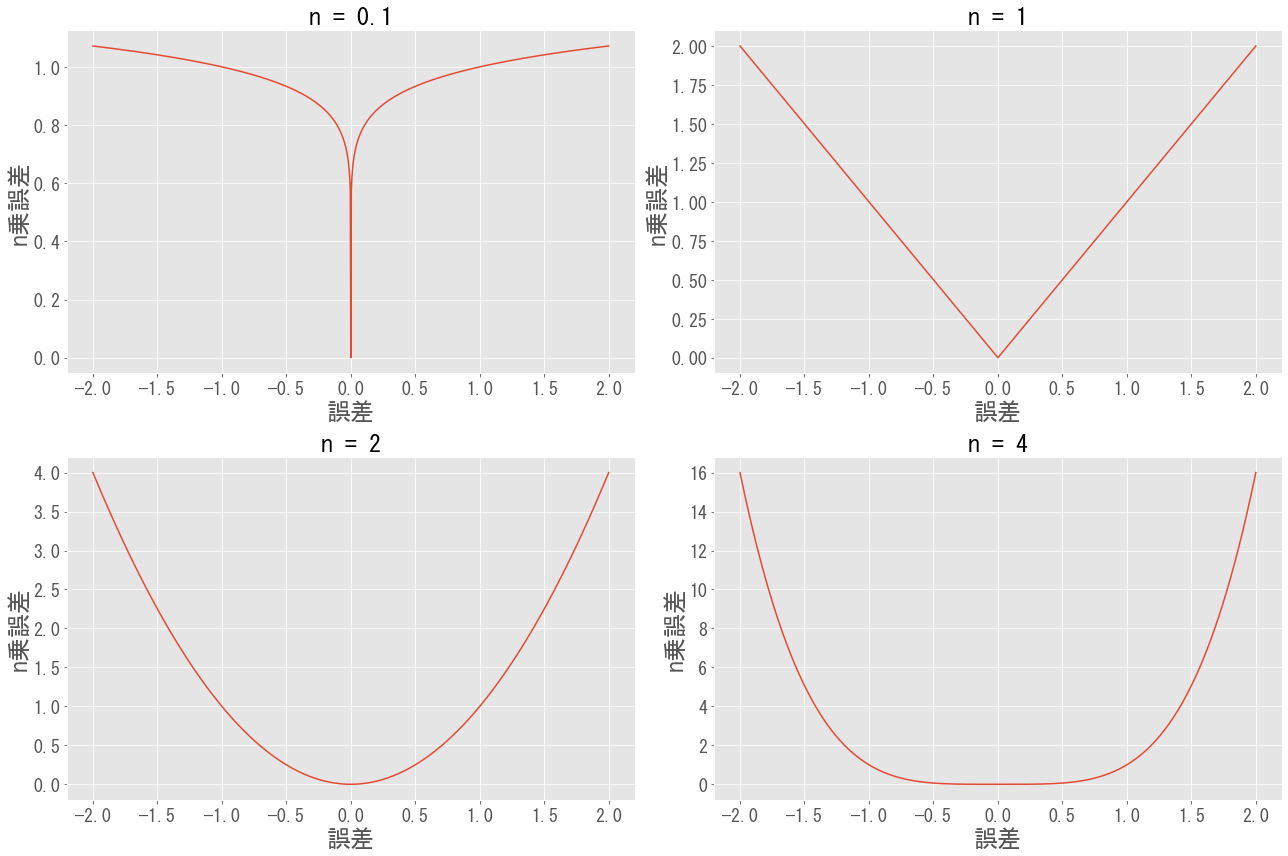
以上を踏まえ,いくつかの$n$に対して最小$n$乗法による予測値$\hat{y}({\bf x})$の性質を議論します.
最小n乗法による予測値の性質
$n = 0, 1, 2, 4$のそれぞれの場合に,最小$n$乗法による予測値$\hat{y}_i$の性質を示します(ただし$n = 0$に関して数学的に怪しい議論をしています).
最小0乗法
$n \to 0$の場合,$| y - \hat{y}|^n$は$y = \hat{y}$のとき$0$,そうでないとき$1$となるため,真値関数$\mathbb{I}$を用いて以下の変形ができるでしょう.
$$
\lim_{n \to 0} | y - \hat{y}|^n = \mathbb{I}(y - \hat{y}) = 1 - \lim_{\epsilon \to 0} \mathbb{I}(|y - \hat{y} | < \epsilon)
$$
$n$および$\epsilon$が十分に小さいものとすると,
\begin{align}
\left. \dfrac{\delta}{\delta \hat{y}} \int p(y \mid {\bf x}) |y - \hat{y}({\bf x}) | ^ n dy \right| _ {\hat{y} = y ^ *}
&\simeq
- \left. \dfrac{\delta}{\delta \hat{y}} \int_{\hat{y} - \epsilon}^{\hat{y} + \epsilon} p(y \mid {\bf x})dy \right| _ {\hat{y} = y ^ *} \\
&= - p(y ^ * + \epsilon \mid {\bf x}) + p(y ^ * - \epsilon \mid {\bf x}) \\
&\simeq - \left. 2 \epsilon \dfrac{d }{d \hat{y}} p(\hat{y} \mid {\bf x}) \right| _ {\hat{y} = y ^ *} \\
&= 0
\end{align}
が成り立ちます.つまり,
$$
\left. \dfrac{d }{d\hat{y}} p(\hat{y} \mid {\bf x}) \right| _ {\hat{y} = y ^ *} = 0
$$
が導かれます.以上より$n \to 0$の場合,$n$乗誤差を最小化する$y ^ * ({\bf x})$は条件付き最頻値となります:
$$
y ^ * ({\bf x}) = {\rm mode}[y \mid {\bf x}]
$$
最小一乗法
$n = 1$の場合,最小化条件は
$$
\left. \dfrac{\delta}{\delta \hat{y}} \int p(y \mid {\bf x}) |y - \hat{y}({\bf x}) | dy \right| _ {y ^ *} = \int_{-\infty}^{y ^ *} p(y \mid {\bf x}) dy - \int_{y ^ *}^{\infty} p(y \mid {\bf x}) dy = 0
$$
となるため,最適な予測値$y ^ * ({\bf x})$は
$$
\int_{-\infty}^{y ^ *} p(y \mid {\bf x}) dy = \int_{y ^ *}^{\infty} p(y \mid {\bf x}) dy
$$
を満たします.つまり,$y ^ * ({\bf x})$は出力$y$の条件付き中央値となります:
$$
\hat{y}(\bf x) = {\rm median}[y \mid {\bf x}]
$$
(補足)一般化された最小一乗法:分位点回帰
目的関数を一般化し
$$
L = \int p({\bf x}, y) \left( | y - \hat{y}({\bf x}) | + (2 \tau - 1) (y - \hat{y}({\bf x})) \right) d{\bf x} dy
$$
とします($\tau = 1/2$とすると最小一乗法に帰着).少し計算すると,
$$
\int_{-\infty}^{y ^ *} p(y \mid {\bf x}) dy = \tau
$$
が成り立ちます.つまり$y ^ * ({\bf x})$は出力$y$の 条件付き$100 \tau$パーセンタイル値となります.この手法は分位点回帰(Quantile Regression)としてよく知られていますが,最小一乗法の拡張として解釈できる点は興味深く,取り上げました.
最小二乗法
$n = 2$の場合,最適な予測値$y ^ * ({\bf x})$は簡単に求まります.最小化条件は
$$
\left. \dfrac{\delta}{\delta \hat{y}}\int p(y \mid {\bf x}) |y - \hat{y}({\bf x}) | ^ 2 dy \right| _ {y ^ *} = 2 \int p(y \mid {\bf x}) (- y + y ^ * ({\bf x})) dy = 0
$$
と変形されるため,$y ^ * ({\bf x})$は出力$y$の条件付き期待値となります:
$$
y ^ * ({\bf x}) = \int p(y \mid {\bf x}) y dy = \mathbb{E} [y \mid {\bf x}]
$$
最小四乗法
$n = 4$の場合も,最適な予測値$y ^ * ({\bf x})$は(簡単ではないものの)解析的に求まります.最小化条件は
$$
(y ^ * ({\bf x}) - \mathbb{E} [y \mid {\bf x}]) ^ 3 + 3 \rm{Var}[y \mid {\bf x}](y ^ * ({\bf x}) - \mathbb{E} [y \mid {\bf x}]) - \mathbb{E} \left[ (y - \mathbb{E} [y \mid {\bf x}])^3 \mid {\bf x} \right] = 0
$$
です.ここで分布$p(y \mid {\bf x}) $の歪度$\alpha$を
$$
\alpha = \dfrac{\mathbb{E} \left[ (y - \mathbb{E} [y \mid {\bf x}])^3 \mid {\bf x} \right] }{ \rm{Var}[y \mid {\bf x}]^{3/2} }
$$
とすると,三次方程式を解くことで
$$
y ^ * ({\bf x}) = \mathbb{E} [y \mid {\bf x}] + \rm{Var}[y \mid {\bf x}] ^ {1/2} \times \left[ \left(\alpha/2 + \sqrt {(\alpha/2)^2 + 1} \right) ^ {1/3} - \left(-\alpha/2 + \sqrt {(\alpha/2)^2 + 1} \right) ^ {1/3} \right]
$$
が最適な予測値$y ^ * ({\bf x})$となります.さらに歪度$\alpha$が小さい(対称な分布に近い)場合,予測値$y ^ * ({\bf x})$は以下のように近似され,$y ^ * ({\bf x})$は出力$y$の条件付き期待値を歪度で補正したものとなります:
$$
y ^ * ({\bf x}) \simeq \mathbb{E} [y \mid {\bf x}] + \dfrac{\alpha}{3} \rm{Var}[y \mid {\bf x}] ^ {1/2}
$$
直観的な理解を考えれば明らかですが,この補正は歪度が大きい(非対称的な)分布の場合,大きい$y$の値に引きずられます.そのため,使いどころはかなり限定的かと思います.
(補足)裾が厚い分布の場合,外れ値に引きずられることで収束しづらくなるという点もデメリットとなるはずです.一方,本記事では初めに$N \to \infty$を仮定しているため,漸近的な挙動は議論できていません.
実装
以上で議論した最小$n$乗法の性質を,数値実験により確認します.特に線形回帰の場合を取り扱い,最適化は勾配法(またはグリッドサーチ)を利用します.
実験の設定
入力$x$と出力$y$は,以下の対数正規分布により生成されるものとします:
\begin{align}
p(x) &= \dfrac{1}{\sqrt{2 \pi \sigma_x^2 } x} \exp \left[ - \dfrac{(\log x - \mu_x)^2}{2 \sigma_x^2}\right] \\
p(y \mid x) &= \dfrac{1}{\sqrt{2 \pi \sigma_y^2 } y} \exp \left[ - \dfrac{(\log y - \log x)^2}{2 \sigma_y^2}\right]
\end{align}
やや恣意的に$\mu_y = \log x$と選んだため,$y$の(条件付き)最頻値,中央値,期待値は以下のようにいずれも$x$に比例します.
- 条件付き最頻値:${\rm mode}[y \mid {\bf x}] = x e^{- \sigma_y^2 / 2}$
- 条件付き中央値:${\rm median}[y \mid {\bf x}] = x$
- 条件付き期待値:${\mathbb E}[y \mid {\bf x}] = x e^{\sigma_y^2 / 2}$
よって,線形回帰による予測値$\hat{y} = {\bf w}^t {\bf x}$の集合$F$は,(条件付き)最頻値,中央値,期待値を含みます.最小$n$乗法による最適化がうまくいけば,それぞれは$n = 0, 1, 2$の場合の予測値と一致するはずです.
実装と結果
Pythonにより,上記のデータ生成と最小$n$乗法による線形回帰を実装しました.ただし$n$が小さい場合は勾配法による収束が難しく(後述),グリッドサーチにより最適化しています.コード全体はGitHubにアップロードしています.
N = 10000
# 入力xの分布
mu_x, sigma_x = 0.0, 0.5 # いずれも定数
x_list = lognorm(s = sigma_x, scale = np.exp(mu_x)).rvs(size = N)
# 出力yの分布
mu_y_list = np.log(x_list)
simga_y = 1.0 # 分散は定数
sigma_y_list = simga_y * np.ones(N)
y_list = lognorm(s = sigma_y_list, scale = np.exp(mu_y_list)).rvs()
# プロット用のx,yの値
x_lin_list = np.linspace(min(x_list), max(x_list), N)
X = np.ones((N, 2)) # 定数項を加えた行列
X[:, 1] = x_list
X_pred = np.ones((N, 2))
X_pred[:, 1] = x_lin_list
mu_y_lin_list = np.log(x_lin_list)
sigma_y_lin_list = simga_y * np.ones(N)
# プロット用の最頻値,中央値,期待値
log_norm_mean = np.exp(mu_y_lin_list + 0.5 * sigma_y_lin_list ** 2.0)
log_norm_median = np.exp(mu_y_lin_list)
log_norm_mode = np.exp(mu_y_lin_list - sigma_y_lin_list ** 2.0)
# 最小n乗法をもとに線形回帰の重みを最適化する
def GeneralRegGradientDescent(X, y, init_theta, q, lr = 1e-7, num_iters = 20000):
theta = init_theta
for i in range(num_iters):
y_hat = X @ theta # predictions
delta = y - y_hat # error
grad = q * (np.abs(delta) ** (q - 2.0)) * delta
theta += lr * grad @ X # Update
return theta
n_list = np.array([0.5, 1.0, 2.0, 4.0]) # これらのnに対して実行(nが0に近いとうまく動かない)
y_pred_list = np.zeros((len(n_list), N)) # プロット用にデータを保存
for idx_n, n in enumerate(n_list):
init_theta = np.zeros(2) # 重みパラメータの初期値
theta = GeneralRegGradientDescent(X, y_list, init_theta, q = n)
print(idx_n, n, theta)
y_pred_list[idx_n] = X_pred @ theta # プロット用データに対して予測
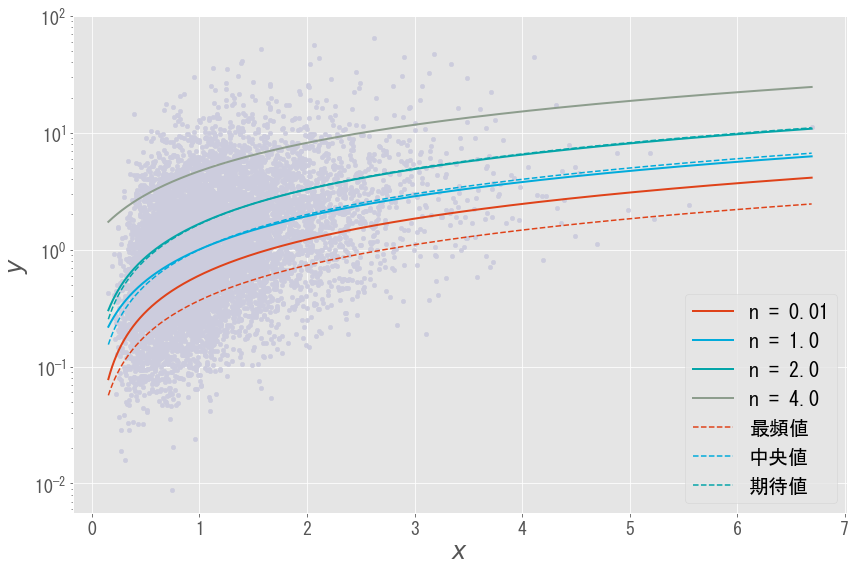
結果は以下となります(線形回帰ですが,対数軸をlogスケールとしているため曲線になっています).確かに$n =1$の場合が(条件付き)中央値,$n = 2$が(条件付き)期待値となっています.なお,$n = 0.01$の場合は最頻値に近いものの,うまく収束していません.
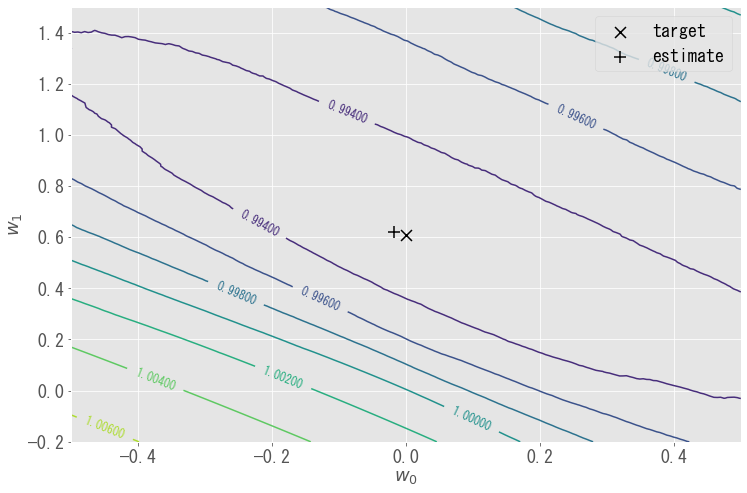
パラメータ${\bf w}$ごとに$n$乗誤差をプロットしたものが下図です.$n$が十分小さい場合,ほとんどの領域で$n$乗誤差は$1$に近くなり,最頻値を与えるパラメータ(target)の周辺でやや$1$より小さくなる程度です.パラメータの変動に対し$n$乗誤差の変動がわずかであり,最小$n$乗法($n \to 0$)の最適化が難しいと理解できます.今回のサンプルに対する最適値(estimate)はtargetにかなり近いですが,さらに近づけるのは大変そうです.
まとめ
この記事では,最小$n$乗法による予測値$\hat{y}(\bf x)$が以下となることを数式と実装から検証しました.
- $n \to 0$の場合,条件付き最頻値:$\hat{y}(\bf x) = {\rm mode}[y \mid {\bf x}]$
- $n = 1$の場合,条件付き中央値:$\hat{y}(\bf x) = {\rm median}[y \mid {\bf x}]$
- $n = 2$の場合,条件付き期待値:$\hat{y}(\bf x) = {\mathbb E}[y \mid {\bf x}]$
最小二乗法は条件付き期待値となり,また解析解が簡単に求まるという点で大きな優位性があります.一方,例えば$n = 1$の場合,予測値が中央値(外れ値に対してロバストな統計量)であるという利点があります.特に出力が外れ値を含むような場合,最小二乗法以外を検討してもよいでしょう.
ただし,本記事では以下に関して踏み込んでいないことに注意が必要です.
- 十分にデータが多いことや,$n$乗誤差を最小化する関数が予測値$\hat{y} = {\bf w}^t {\bf x}$の集合$F$に含まれることなどを仮定している
- 特にサンプル数$N$に対する漸近挙動を議論していない(裾が厚い分布に対し最小$n(\geq2)$乗法が"適していない"ことを議論するには,サンプル数に対する漸近挙動をかんがえる必要がありそう?)
- $n$が$0$に近い場合を含め,ナイーブな最適化手法(勾配法,グリッドサーチ)を用いている
- 確率分布$p(y \mid {\bf x})$に対する性質は議論している一方,実際のデータ$(X, {\bf y})$に対する性質は議論していない
- $n \to 0$の議論が成り立つ正確な条件を明確にしていない
上記をクリアにするのは割に合わなさそう(かつ実力が及ばなさそう)であるため,いったん今後の課題としておきます.本記事に不正確な点や,補足事項などあればぜひご指摘ください.
参考とした記事
以下の記事は最小$n$乗法や分位点回帰について詳しく,参考としました.
またTheory of Point Estimation(Springer)のp.228で,$n = 0, 1, 2$に対応した命題が示されています.
特に最小一乗法について,以下の博論に詳しくまとまっています.
なお最小0乗法について,一般的には最頻値には収束しないことをC. HEINRICH(2013)で取り扱っているかと思いますが深堀できていません...
こちらはご参考ですが,誤差関数をより一般的な形にしたロバスト回帰について,以下記事で説明されています.
(2023年11月20日追記)外れ値の影響に関する議論の中で,「裾の厚さ」と「分布の非対称性」を混同している箇所があったため修正しました.貴重なご指摘ありがとうございます!