pohotos by Ronnie Macdonald

「AIが人間の仕事を奪う」と言われ始めてしばらく経ちますが、今や「幻滅期に入った」なんて言われ方もしています。おかげで僕は仕事を奪われることもなく、毎日満員電車に揺られています。奪う奪う詐欺もいいとこです。

そんなAIの発展にはもう少し時間がかかりそうな一方で、学べる環境は簡単に手に入るようになりました。触るなら、皆が幻滅しかかっている今な気もします。ということで、今更ですがAIの力を知るべく、ディープラーニングに触れてみることにしました。

いろいろ試したのですが、ここでは結果をメインに「無知の状態から勉強しても、ディープラーニングでこれぐらいは楽しめるよ」ということを伝えてみます。プログラムはお手本になるようなものではないので、見たい人だけに有料で公開してみます。

Kaggleでディープラーニングのお手並み拝見

最初にディープラーニングの基礎となる数学を少し勉強しました。いやー…なかなか心折れますね。数式に次ぐ数式。知らなくてもコードは書けますが、数学的な意味を知っておくと理解が進むので、概要だけでも学んでおいて損はないんだろうなーというのが感想です。

ということで軽く勉強後、まずはディープラーニングの力を確かめるために、機械学習で有名なお題「タイタニックの生存者予測」で試してみることに。各乗客の年齢や性別などの属性をもとに、誰が生き残ったのかを予測するやつ。

環境はGoogle Colaboratory、実装は最も簡単そうなTensorFlowを使います。Googleのチュートリアルを参考にするだけで簡単に作れました。予測結果をアップロードすると、スコアが返ってきます。

正解率76.5%。初心者が適当に作ったモデルで8割近く正解です。パラメータやデータを調整すればもっと上がるでしょう。

本来は、「女性や子供が優先して助けられたのでは？」とかいろいろ考えて試行錯誤で分析するんですが、そこをまるごとディープラーニングがやってくれたわけです。確かにディープラーニング、結構すごい。

すごいけど、面白くない

もっと触ってみたいと感じる一方で、この予測をしていて、僕は大きな問題を感じました。

面白くない…。ディープラーニングが、ではなく、テーマが面白くないんです。100年以上前に沈んだ海外の船の乗客の生死を予測しても、全っ然面白くない！

「ジェームス…お前死んだと思ってたのに…生きてたのか！」とか「レイナ…なんで死んじまったんだよぉぉー！！」みたいに一喜一憂するわけにもいかないじゃないですか。誰も知らないし。もう全員死んどるし。てかそもそもKaggleは正解教えてくれないし。

もっとわくわくするテーマがいいなぁ…。ということで、前々からやってみたかった、お金に絡むこのテーマに。

ディープラーニングを使って競馬で回収率100%を超えてみる

競馬は控除率が20%ぐらいらしいので、リターンは平均80%スタートです。回収率100%を超えるのは割と厳しいはず。でも過去のデータは山ほどあるはずだし、ディープラーニングならやってくれるのでは？という期待を込めて試してみます。

ゴールは「複勝馬券で回収率100%を超えること」。

競馬の特性上、複勝よりも配当が大きな馬券を狙った方が効率的なのかもしれませんが、当たりやすい馬券でないと面白くなさそうなので複勝に絞りました。

対象データ

学習用：2010～2017年
検証用：2018～2019年（11月初旬まで）

検証用データで100%超えを目指します。まずはネットでスクレイピングして、こんなデータを揃えました。

分類	項目
馬情報	馬番
	枠番
	年齢
	性別
	体重（現在）
	体重（前走との差分）
	負担重量
当日レース情報	レース場
	出走馬数
	コース距離
	コース種類
	コースタイプ（ダ/芝/障）
	天気
	馬場状態
同馬の過去レース情報（×5走分）	オッズ
	人気
	順位
	タイム（秒）
	着差
	前走からの経過日数
	コース距離
	コース種類
	コースタイプ（ダ/芝/障）
	天気
	馬場状態

※当日の「オッズ」や「人気」は勝敗に直接関係ないと判断して省いています。
※この記事での「オッズ」は単勝オッズを指します。

3着以内の馬を予測

このデータをインプットに、ディープラーニングで「3着以内かどうか」を予測します。予測値は0～100の数値（これを「3着指数」と呼ぶことに）にしました。この値が大きいほど、3着以内になりやすいはず。

ちなみにディープラーニングの核となる、予測モデル作成部分のコードは、たったこれだけ。

import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.Dense(300, kernel_regularizer=tf.keras.regularizers.l2(0.001), activation=tf.nn.relu, input_dim=len(train_df.columns)),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(300, kernel_regularizer=tf.keras.regularizers.l2(0.001), activation=tf.nn.relu),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

model.compile(
    loss='binary_crossentropy',
    optimizer=tf.keras.optimizers.Adam(),
    metrics=['accuracy'])

fit = model.fit(train_df,
    train_labels,
    validation_data=(valid_df, valid_labels),
    epochs=30,
    batch_size=32)

※シグモイド関数の出力結果を100倍したものを3着指数としています。

全レースで購入してみる

作成したモデルで、レースごとに3着指数が最も大きい馬券を購入してみます。2018年以降の全レースでシミュレーションした結果がこれです。

項目	結果
対象レース数（※）	3639
対象レコード数	41871
購入数	3639
的中数	1976
的中率	54.3%
回収率	82.7%

※欠損値（過去レース情報含む）のない馬が5頭以上のレースのみを対象としています。

そこそこ的中していますが、回収率が伸びません。そもそも3着指数と、的中率（実際に3着以内であった割合）や回収率がどのような関係になっているのか気になります。

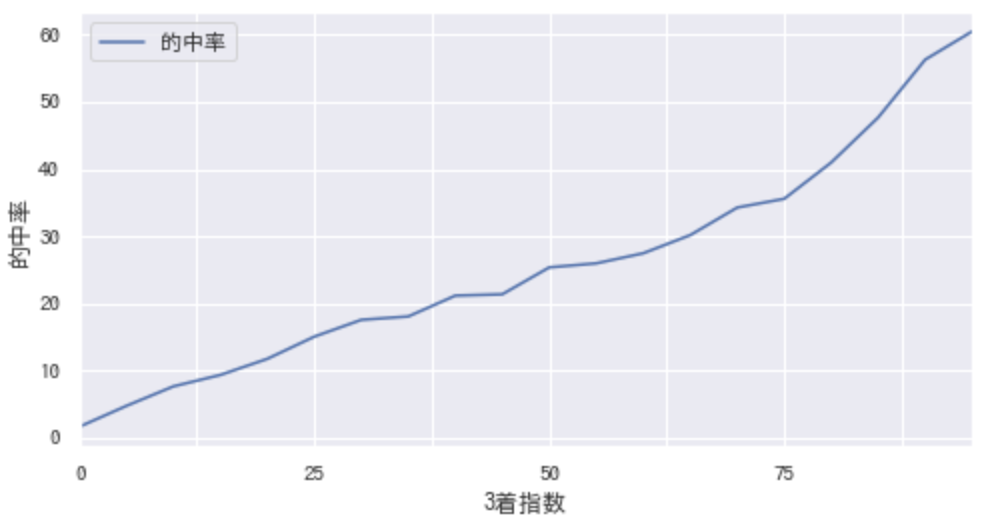
3着指数と的中率/回収率の関係

3着指数と的中率の関係はこのようになっていました。

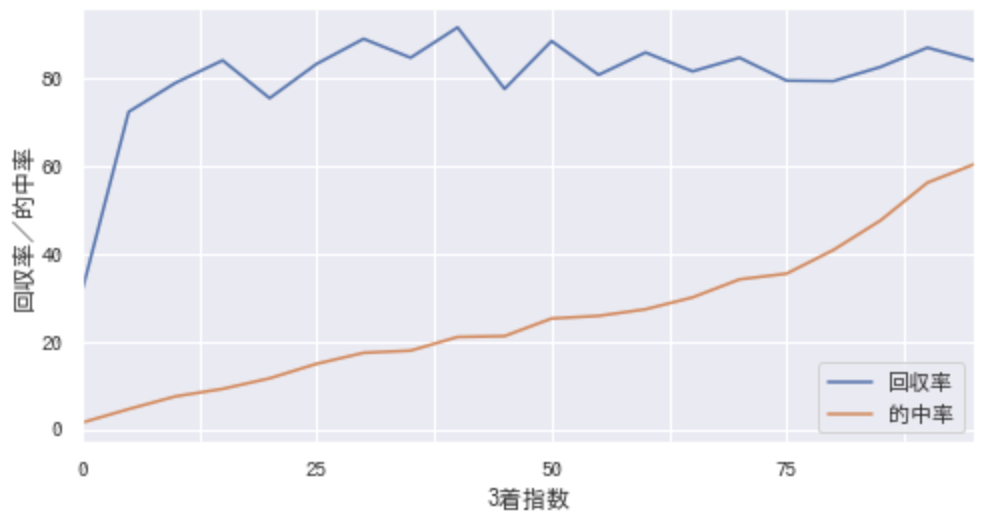
3着指数が高いほど的中率が上がっているので、3着以内を当てるモデルとしては機能していそう。それなら、この指数が高い馬に絞って買えば、回収率100%を超えるのか？

先程のグラフに、平均した回収率を加えてみます。

回収率は、的中率にあまり関係なく80%～90%付近に。つまり、3着指数が高い馬（勝ちそうな馬）ほど、リターンが小さいということになる。

となると、この指数と的中率の関係は、オッズと的中率の関係に似ている気がします（オッズは低いほどリターンが小さい）。ということで一応、3着指数と平均したオッズとの関係を調べてみると…

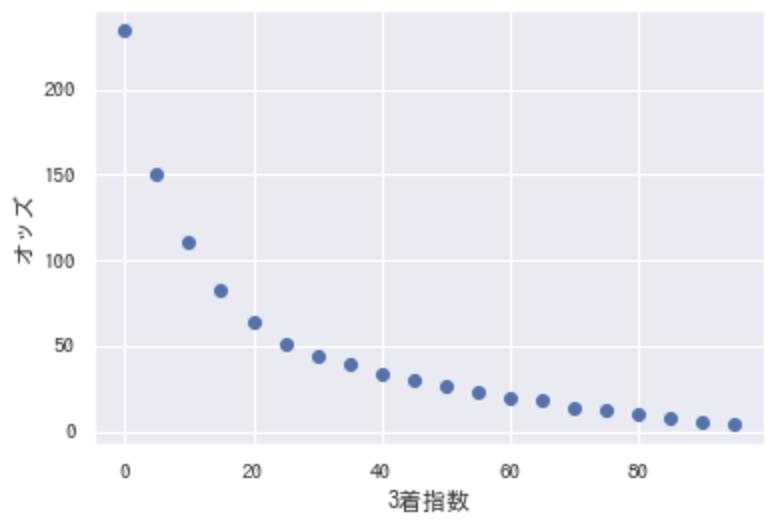
反比例のグラフに。やはり3着指数が高い馬はオッズが低い。オッズを見ずに予測しても結局こうなるんですね。面白いけど、これが競馬の難しさでもありそう。

回収率100%を超えるために

3着指数とオッズがほぼ反比例なのはわかりました。でもそれは平均オッズの話。ひとつひとつを見れば、「3着指数が高い割に、オッズも高い馬」も存在するはず。回収率を上げるには、そのようなオッズの歪みを突くのが良さそうです。

ですが、例えば3着指数が70以上、オッズが100以上の馬券をすべて買うと、こんな悲惨な結果になります。

項目	結果
購入数	73
的中数	1
的中率	1.37%
回収率	16.9%

オッズがとても高い馬は、たとえ指数が高くても的中率が低いようです。高いオッズには、それなりの理由があるのでしょう。逆にオッズが低すぎると、当然配当が少なく回収率が上がりません。であれば、狙うは中間です。

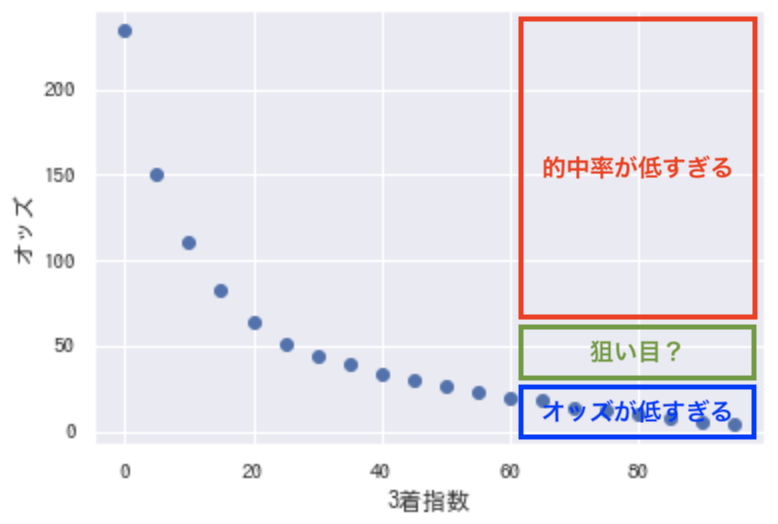
（以降、他の方から予測対象に対する指摘をいただいたため、対象を広げた結果に修正しています）

2018年の予測結果で3着指数が60以上、かつオッズが高すぎない一部の範囲（55〜60あたり）に絞ってシミュレーションしてみたところ、回収率213%となり、かなり良い感じに。

項目	結果
購入数	44
的中数	10
的中率	22.7%
回収率	213.6%

とはいえこれは2018年の良いとこ取りなので、良い結果で当たり前。ですが同じ予測方法で、2019年でもシミュレーションしてみたところ、こちらも回収率194%に。2年トータル（約22ヶ月）ではこうなりました。

項目	結果
購入数	99
的中数	19
的中率	19.2%
回収率	202.63%

これで、無事に目標にしていた回収率100%を超えました。ちなみに2018年以降、この予測に従って毎回100円ずつ買った場合の収支グラフはこうなります。大きく下げることなく、安定して上昇しています。

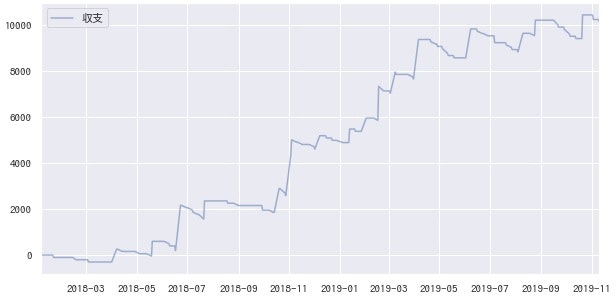
この2年間が好調な可能性もゼロではありませんが、ここまで階段状であればある程度信用できそうです。購入数は多くはない（月に4回程度）ですが、勝てない敵を選ばないことは勝つための必須条件でもあるでしょう。

（おまけ）配当が高い馬を予測

これで終わってもいいのですが、せっかくなので、3着予測とは別のパターンとして「配当の期待値」の予測も試してみます。

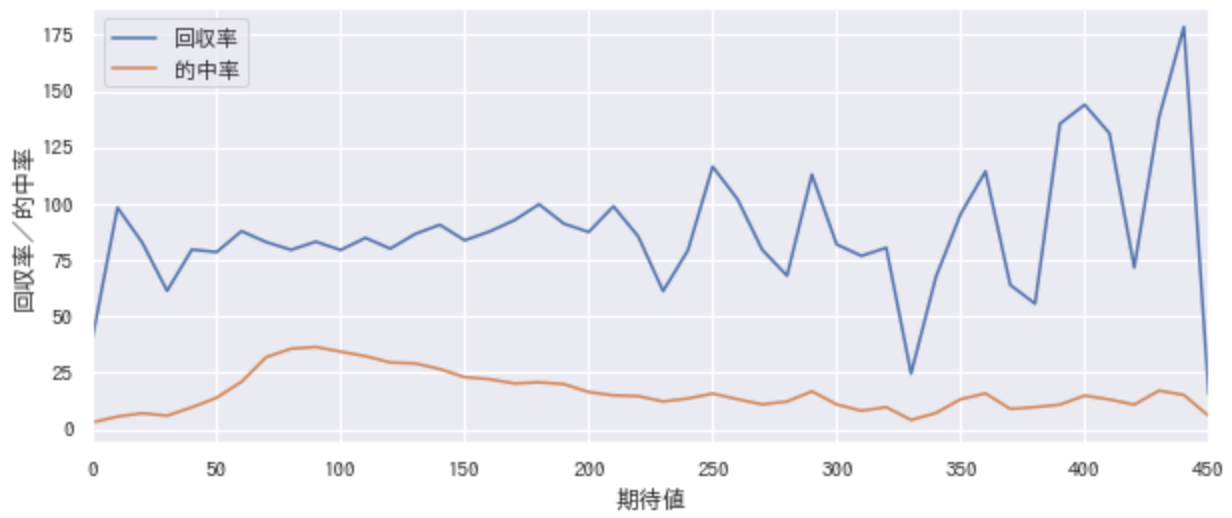
オッズもインプットに含めたデータをディープラーニングに与えて予測した結果を、先ほどと同じようにグラフ化してみます。オッズが高くても勝ちそうな馬が、期待値高めになっているように見えます。（グラフ横軸はまだ先がありますが、省略しています）

期待値と、回収率／的中率の関係です。

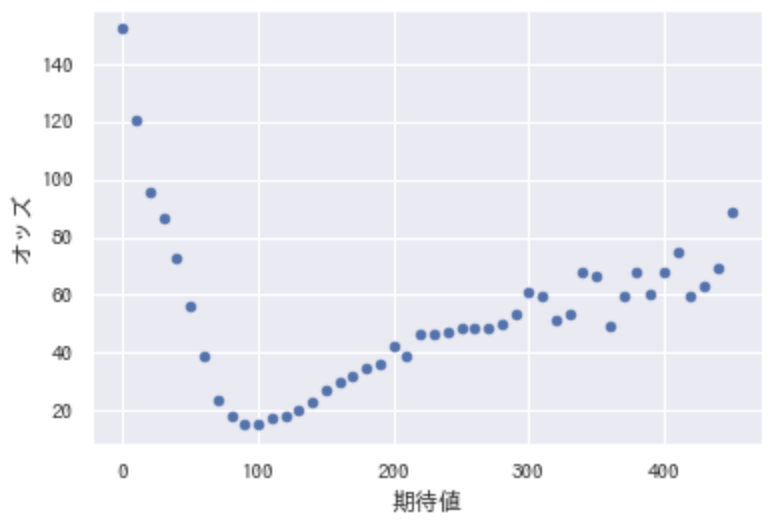
右肩上がりの回収率を見る限り、期待値が高い馬券を永遠に買い続ければ回収率が高まりそうですが、こちらも1〜2年程度では数が少なく安定しないみたいです。

仮にグラフ上で成績の良い期待値が390～450の馬を全て購入すれば、一応100%を超えますが、局所的な上昇に見えるので継続的な安定はなさそうです。

項目	結果
購入数	275
的中数	37
的中率	13.5%
回収率	131.1%

収支も3着指数のときより乱高下します。オッズ高めを狙うので、当てたときのリターンは大きいんですが。

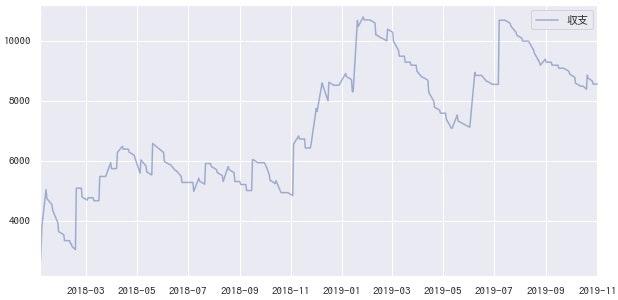
やったことは以上です。

プログラムはこちら

3着指数の予測モデル作成と検証までのプログラム（Python）は、実験的に有料で下記ページで公開しています。教科書的に使えるような美しいものではないので、お金と心に余裕がある好奇心の強い暇な方だけ見てください。

ディープラーニングさえあれば、競馬で回収率100%を超えられる（プログラム）

後日談はこちら

あとがき

最近、QR決済の多額のキャンペーン合戦により、やっとモバイル決済が普及してきました。決済以外でも、何を流行らせるにも還元やクーポンが乱発される様子を見て、人を動かすのは、まだ「お金」なんだなぁと改めて感じてから、次はお金絡みの記事を書こうと思っていたので、こうして書けて満足です。

今回の予測のインプットには、「馬名」「騎手名」を含んでいません。つまり馬の血統や騎手の戦歴、相性なども考慮すれば、さらに精度の高い予測ができるでしょう。また、欠損データの補完やバッチ正規化あたりはもちろん、単純にディープラーニングとしてのパラメータ調整だけでも向上すると思いますし、複勝以外の馬券も期待できます。要するに、伸びしろがまだまだあります。

便利な反面、1点だけ気になったのは、こうして競馬をAIで予測していると「自分の頭で予想する楽しみ」が損なわれるんじゃないか、ということでした。自身の直感、馬への愛着など、自分から溢れる想いと共に選んだ馬が勝ったときの喜びは、AIでは得られない気がします。

いずれ誰もが、あらゆる未来予測にAIを使い出したとき、それでも人々は、今のように競馬場に集まり、我を忘れて熱狂し続けられるんでしょうか。あの大量の馬券が空に舞う姿は、いつまで見られるんでしょうか。迫り来るAIの波に、仕事だけでなく心まで奪われないよう、うまく活用していきたいものです。