TL;DR
- 識別モデルでは事後確率をそのままシグモイド関数/ソフトマックス関数でモデル化する。重み$w$は負の対数尤度(誤差)最小化で求める、という進め方はこれまでと同じ。
- ただし、誤差最小の点を求めるための「誤差関数の微分=0」の方程式は解析的に一発で求められない。なので、繰り返し手法を使って求める。
4.3 確率的識別モデル
4.2節で扱った生成モデルでは、事前確率$p(C_k)$とクラスの条件付き確率$ p(x|C_k) $を仮定し、ベイズの定理を使って事後確率$ p(C_k|x) $を求めて分類した。
識別モデルでは、事後確率$ p(C_k|x) $を直接仮定する。
識別モデルの利点は、
- 決めるべきパラメータが生成モデルより少ないこと
- クラスの条件付き確率$ p(x|C_k) $の推定が困難でもよい予測性能を示す場合があること
4.3.1 固定基底関数
(データの分布に応じて基底関数を動的に変えるのではなく)あらかじめ定めた基底関数ベクトル$ \Phi(x) $を使って入力の非線形変換を行おう。
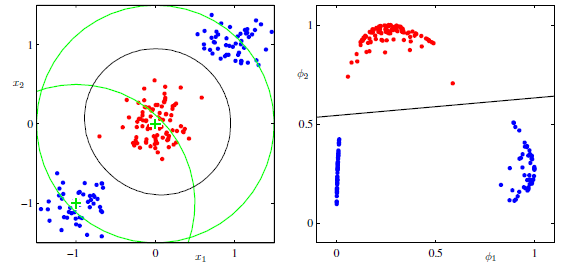
入力空間上では線形分離不可能であった問題が、非線形変換後の特徴空間上では線形分離可能になることがある(下図)。決定境界は入力空間上では非線形になるが、特徴空間において線形になる。
~図の見方~
左図が入力空間での赤クラスと青クラスの分布を示している。入力データにガウス基底関数を2つ適用する。
左図中央の緑十字が2つめのガウス基底関数$\phi_2$の山の部分を示している。赤データはガウスの山付近に集まっているので、右図の特徴空間上の縦軸$\phi_2$において赤クラスは大きな値をとっている。
一方、青クラスは緑十字から離れているので特徴空間上の縦軸の値はあまり大きくない。
次に左図左下の緑十字は1つめのガウス基底関数$\phi_1$の山の部分を示している。青クラスのかたまりのうち、片方はこの十字の近くに位置するので、特徴空間の横軸$\phi_1$が1に近い大きな値。青クラスのもう1つのかたまりは十字から最も離れた位置にあるので、特徴空間上の縦軸は0に近い値。
このような非線形変換の結果、青クラスと赤クラスが線形分離可能になっている。
~ここまで~
基底関数を適切に選択すれば、クラス間の離れ具合が改善され、事後確率のモデル化が簡単になる。
ただし、線形分離可能な基底関数を探索するには、入力次元に対して指数的に基底関数の数を増やす必要がある(次元の呪い)。
4.3.2 (2クラス)ロジスティック回帰
2クラス分類問題における一般化線形モデルを扱ってみよう。
4.2節の式(4.57)より2クラス問題の事後確率はシグモイド関数で書ける(参照:part15)。
つまり、
$$
p(C_1 | \phi) = \sigma(w^T \phi) \tag{4.87}
$$
このモデルは分類のためのモデルであるが、ロジスティック回帰 (logistic regression) と呼ばれる。
ロジスティック回帰の利点はパラメータ数がすくないこと。特徴ベクトル$\Phi$がM次元だった場合、ロジスティック回帰で推定すべきパラメータは$w$のM個。
一方、ガウス分布でクラスの条件付き確率密度を推定する生成モデルのアプローチでは、ガウスの平均や共分散行列、事前確率の総計$ M(M+5)/2 + 1$個のパラメータを推定しなければならない。
次に、ロジスティック回帰のパラメータ$w$を最尤法で求める方法を扱う。...が、結論を先に言うと、最尤法では過学習してしまう。
準備として、まずシグモイド関数の微分を行う。
演習4.12:シグモイド関数の微分は?
シグモイド関数は以下の定義である。
\begin{align}
\sigma(a) &= \frac{1}{1+ \exp(-a) } \tag{4.59} \\
\frac{d\sigma}{da} &= \left[ \{ 1 + \exp( -a ) \}^{-1} \right]'
= (-1) \cdot \{ 1 + \exp( -a ) \}^{-2} \cdot (-1) \cdot \exp(-a) \\
&= \frac{ \exp(-a) }{ \{ 1 + \exp( -a ) \}^{2} }
= \frac{1}{ 1+\exp(-a) } \left\{
\frac{1+\exp(-a)}{1+\exp(-a)} - \frac{1}{1+\exp(-a)}
\right\} \\
&= \sigma (1 - \sigma ) \tag{4.88}
\end{align}
訓練データ集合$ \{ \phi_n, t_n \}, t_n \in \{0, 1\}$であり、$ \phi_n = \phi(x_n) $とすると、尤度関数は
$$
p( \mathbf{t} | w) = \prod_{n=1}^N \sigma(w^T \phi_n)^{t_n} \{ 1 - \sigma(w^T \phi_n) \}^{1-t_n} \tag{4.89}
$$
ここで、$\mathbf{t} = (t_1, \cdots, t_N)^T $である。尤度の負の対数をとって誤差関数とする。
$$
E(w) = - \ln p(\mathbf{t} | w) = - \sum_{n=1}^N \{
t_n \ln \sigma(w^T \phi_n) + (1 - t_n) \ln (1 - \sigma(w^T \phi_n) ) \}
\tag{4.90}
$$
この誤差関数はクロスエントロピー誤差関数と呼ばれ、深層学習でも非常によく用いられる。
演習4.13:誤差関数のwに関する勾配の式を導出する
$ y_n = \sigma(a_n), a_n = w^T \phi_n$のとき
\begin{align}
\frac{d y_n}{dw} &= \frac{d \sigma(w^T \phi_n )}{dw} = \frac{d \sigma(a_n)}{d a_n} \cdot \frac{d a_n}{dw} \\
&= \sigma(a_n) ( 1 - \sigma(a_n) ) \cdot \phi_n \\
&= y_n( 1 - y_n) \phi_n \\
\\
E(w) &= - \sum_{n=1}^N \{
t_n \ln y_n + (1 - t_n) \ln (1 - y_n ) \} \\
\frac{d E(w)}{dw} &= - \sum \left\{
t_n \frac{1}{y_n} \frac{d y_n}{dw} + (1 - t_n) \frac{1}{1 - y_n} \frac{d(1-y_n)}{dw}
\right\} \\
&= - \sum \left\{
t_n \frac{1}{y_n} y_n( 1 - y_n) \phi_n + (1 - t_n) \frac{1}{1 - y_n} (-1) y_n( 1 - y_n) \phi_n
\right\} \\
&= \sum (y_n - t_n) \phi_n \tag{4.91}
\end{align}
注意点。
いつもどおり、式(4.91)=0、の方程式を解いて尤度を最大にするwを求めたい...が、(4.91)の$ y_n = \sigma (w^T \phi_n) $が非線形であることから、方程式が解けない(=解析的に最尤解を導出できない)。
なので、ニュートン-ラフソン法と呼ばれる手法で解を求める⇒4.3.3節にて。
最尤推定によって求めたパラメータ$w$は過学習を起こしてしまう。
式(4.89)より、すべての$ \sigma(w^T \phi_n) = p(C_1 | \phi_n )$が正解値と一致する、すなわち0か1になるとき尤度が最大となる。つまり、各クラス$k$のすべての学習データが、事後確率$ p(C_k|x) = 1$に割り当てられることになる。
これは、回帰問題の多項式曲線フィッティングでいえばすべての訓練データを誤差0で通るような曲線にフィッティングしていることに相当し、未知のデータへのフィッティング性能が著しく低くなっている。
過学習を避けるには、これまで学んできたように正則化項を加えるとよい。
4.3.3 反復再重み付け最小二乗
上節で述べた通り、式(4.91)はもはや解析的には解けない。
なので、機械学習の分野でよく使われる反復的なアプローチで解を求める。
その流れは、
- 適当に初期値$x_0$を決める
- 初期値から微分とかを使って、初期値よりは解に近い値$x_1$を求める
- 導出した解に近い値$x_1$から微分とかを使って、さらに解に近い値$x_2$を求める
- 解の更新が収束するまで上ステップを繰り返す
ここでは、ニュートン-ラフソン法 (Newton-Raphson method) と呼ばれる反復法を用いる。
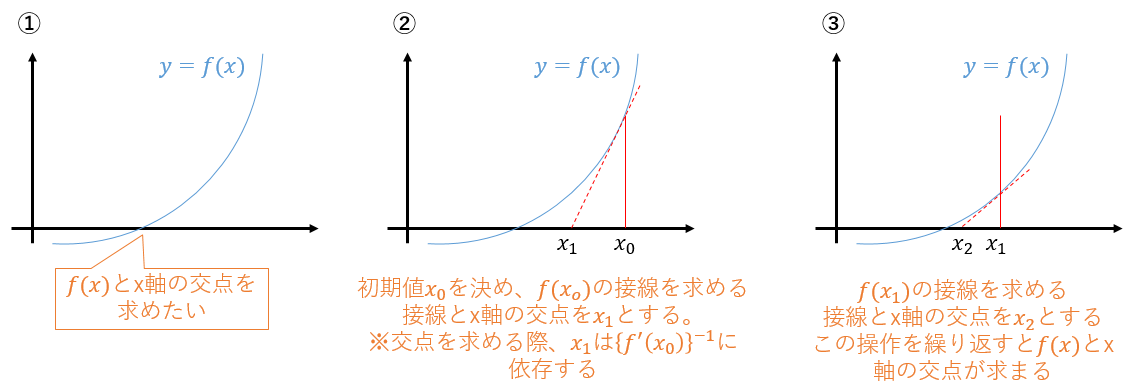
この手法のやっていることを下図に示す。
ある関数$f(x)$が$f(x)=0$となる座標$x$を求めたいときに使える手法で、$f(x)$の微分(接線)の逆数を使って求めることを覚えておこう。
(※なんで微分の逆数がでてくるか?の参考リンク。スライドP.5参照)
式(4.90)のクロスエントロピー誤差関数は下に凸な関数であることが分かっている。
なので、誤差関数が最小になる点では誤差関数の勾配が0になる。
そこで、誤差関数の勾配を$f(x)$と見なして、勾配が0となる点($f(x)$とx軸の交点)を求めたい。
ニュートンラフソン法で、1次微分である勾配が0となる$w$を求めたいので、勾配の微分、すなわち$E(w)$の2回微分が必要である。
$E(w)$の2回微分を要素とする行列をヘッセ行列とよび、$H$とおくと、ニュートンラフソン法による$w$の更新式は以下になる。
$$
w^{(new)} = w^{(old)} - H^{-1} \nabla E(w) \tag{4.92}
$$
※微分の逆数が出てくることが、上式では$H^{-1}$に代わっていることに留意。
クロスエントロピー誤差関数の勾配とヘッセ行列は1
\begin{align}
\nabla E(w) &= \sum_{n=1}^N ( y_n - t_n) \phi_n = \Phi^T (\mathbf{y} - \mathbf{t} ) \tag{4.96} \\
H &= \nabla \nabla E(w) = \sum_{n=1}^N y_n (1 - y_n) \phi_n \phi_n^T
= \Phi^T R \Phi \tag{4.97}
\end{align}
となる1。ここで、要素が以下の式で与えられる対角行列$R$を導入した。
$$
R_{nn} = y_n ( 1 - y_n) \tag{4.98}
$$
よって、ロジスティック回帰モデルのニュートンラフソン法による$w$の更新は
$$
w^{(new)} = w^{(old)} - (\Phi^T R \Phi)^{-1} \Phi^T (\mathbf{y} - \mathbf{t} )
\tag{4.99}
$$
更新式(4.99)に出てくる重み付け行列$R$は定数でなく、$w$に依存しているので、$w$が更新されるたびに$R$を計算し直して、繰り返す解く必要がある。
このことから、このアルゴリズムは反復再重み付け最小二乗法 (iterative reweighted least squares method; IRLS) と呼ばれる。
4.3.4 多クラスロジスティック回帰
4.3.2節「(2クラス)ロジスティック回帰」と同じ流れなのでさらっと。
多クラスに拡張した尤度関数の負の対数をとったものを誤差関数とする。この誤差関数もクロスエントロピー誤差関数とよばれる。
2クラスの場合は、事後確率がシグモイド関数で表されたので、誤差関数の勾配の導出にシグモイド関数の微分が現れた。
一方、多クラスの場合は事後確率がソフトマックス関数で現れたので、誤差関数の勾配の導出にはソフトマックス関数の微分が現れる。
誤差関数の微分が0になるような重み$w$を反復再重み付け最小二乗法を用いて求める。
4.3.5 プロビット回帰
...よく分からない...。とくに、以下の閾値の話は間違ってる可能性多々あります
ロジスティック回帰モデルとよく似た性質のプロビット回帰モデルについて扱う。
ただし、プロビット回帰の方が外れ値に敏感らしいので、あまり使われない(?)
(少なくとも私は、ロジスティック回帰は使うが、プロビット回帰は使ったことがない)。
2クラス問題で考える。これまでは入力データ$x_n$に対しての目的変数$t_n$は決まったものとしていた。
ここからは、目的変数は$x_n$から計算した値$ a_n = w^T \phi_n = w^T \phi(x_n) $によって設定されるとする。
\begin{align}
\begin{cases}
t_n = 1 & a_n \geq \theta \\
t_n = 0 & else
\tag{4.112}
\end{cases}
\end{align}
つまり、$a_n$がある閾値$\theta$以上か未満かで目標変数が設定される。
さらに、その閾値$\theta$もある確率密度$ p(\theta) $の累積分布関数で与えられるとする。つまり、
$$
\theta = f(a_n) = \int_{ - \infty}^a p(\theta) d\theta \tag{4.113}
$$
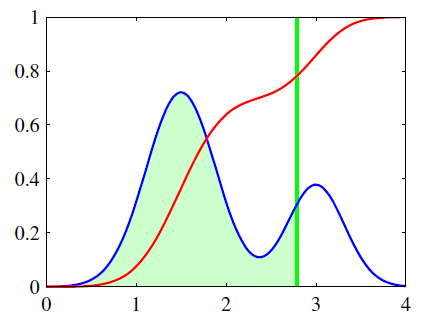
ある確率密度$ p(\theta) $が下図の青線のように混合ガウス分布であったとしよう。
おそらく、こういう流れ。
- 入力データ$x_n$から$ a_n = w^T \phi_n = w^T \phi(x_n) $を求める。$a_n = 2.8$になった(緑線)。
- 続いて閾値$\theta$を求める。累積分布関数は赤線であり、$f(2.8) = 0.8$ぐらいとなった(緑と赤線の交点)。
- $a_n = 2.8 > f(2.8) = 0.8$なので目標変数は$t_n = 1$と設定される
- 目標変数等を使って、何らかの更新式で重みをアップデート
ここで、確率密度$ p(\theta) $が平均0, 分散1のガウス分布で与えられるときは、プロビット回帰モデルと呼ばれる(?)。
平均0, 分散1のガウス分布の累積分布関数はシグモイド関数とよく似た形となるため、得られる結果はロジスティック回帰の結果とよく似たものとなる。
しかし、ガウス分布の累積分布関数の方がシグモイド関数と比べて、急激に0または1に漸近する性質の影響で、外れ値に敏感らしい。
4.3.6 正準連結関数
3章「線形回帰モデル」で扱った、ノイズがガウス分布としたときの線形回帰モデルに対して、尤度は式(3.11, 3.12)の形で書けることを導出した(参照⇒part8)。
\begin{align}
\ln p (t | X, w, \beta) &= \frac{N}{2} \ln \beta - \frac{N}{2} \ln (2 \pi )
- \beta E_D (w) \tag{3.11} \\
E_D (w) &= \frac{1}{2} \sum_{n=1}^N \{ t_n - w^T \phi (x_n) \}^2 \tag{3.12}
\end{align}
誤差関数を負の対数尤度としよう。誤差関数を$w$について微分すれば
$$
\nabla_w E_D(w) = \sum_{n=1}^N \{ t_n - w^T \phi (x_n) \} ( - \phi (x_n) )
= \sum_{n=1}^N \{ w^T \phi (x_n) - t_n \} \cdot \phi (x_n)
$$
となり、「誤差」$w^T \phi (x_n) - t_n = y_n - t_n$と特徴ベクトル$\phi(x_n)$の積の形となる。
2クラス問題のときのシグモイド関数を活性化関数としたときの誤差関数も式(4.91)より、誤差と特徴ベクトルの積の形となっている。(多クラス問題のソフトマックス活性化関数も同じ形になる)
誤差関数の微分が誤差と特徴ベクトルの積の形となる性質は、以下の2条件を満たしたときに得られる一般的な結果である。
- 正準連結関数 (canonical link function) という関数を活性化関数に選ぶ
- 目的変数に対する条件付き確率分布に指数型分布族を選択する。
指数型分布族は式がごちゃっとしており、イメージがわきにくいため、本記事のシリーズでは深く扱っていない。なので、上記が成り立つ証明(式変形)は略。
正準連結関数って何者?っていうイメージだけつかもう
一般化線形モデルは入力$x$あるいは特徴$\phi$の線形結合$w^T \phi$を非線形関数$f$にいれたものが出力$y$となるモデルと定義する。つまり、
$$
y = f(w^T \phi) \tag{4.120}
$$
ここで、$f$は活性化関数とよばれ、連結関数とは活性化関数の逆関数のことである。すなわち、$ f^{-1}(y) = w^T \phi$である。
指数型分布族の形を決めるパラメータの1つ$\eta$と予測値$y$の間にはある関係式が成り立つ。なので、その関係を$ \eta = \psi(y)$としよう。
このとき、連結関数$ f^{-1}(y) $が$ f^{-1}(y) = \psi(y) $を満たすときが正準連結関数とよばれる。
少し言葉を変えると、
出力$y$から目的変数に関する条件付き確率分布(指数型分布族)の形を決めるパラメータを求めるときの対応関係(関数)と
出力$y$から入力$w^T \phi$を求めるときの対応関係(関数)が同じであれば正準連結関数である。
(自信なし)4.3節の目的変数の条件付き確率密度が式(4.89)や(4.107)のように二項分布(指数型分布族)の形になっているが、二項分布の形を決めるパラメータと出力の関係が、シグモイド活性化関数やソフトマックス活性化関数の連結関数から入力を求める関係と同じということか?