TL;DR
- 入力$x$に対して非線形な基底関数とパラメータ$w$の線形結合で表される線形モデルを考える
- パラメータ$w$の誤差最小二乗の最尤推定は正規方程式と呼ばれる式で得られる
3 線形回帰モデル
この章で扱うのは回帰問題。回帰問題は例えば、A社の株価、B社の株価などを説明変数$x$として、実数値であるZ社の株価$y$を推定したい、といったような問題。他にも1章で扱った観測値$x$からある実数値を出力する関数にフィッティングし、関数の出力$y(x, w)$を推定する問題も回帰問題の一例である。
大まかな流れは1章の多項式曲線フィッティングと同じで、
- 一般化線形モデル$y(x, w) = \sum_{j=0}^{M-1} w_j \phi_j (x) = w^T \phi(x)$で
入力$x$から出力$y$を推定するとモデル化 - モデルのパラメータである$w$を最尤推定(3.1.1節)
- 過学習を避けるため、正則化をいれて$w$を推定(3.1.4節)
- 正則化係数$\lambda$をどう決めるかが不明 ⇒ 3.3節「ベイズ線形回帰」へ
3.1 線形基底関数モデル
最も単純な線形回帰モデルは
$$
y(x, w) = w_0 + w_1 x_1 + \cdots + w_{M-1} x_{M-1} = w_0 + \sum_{j=1}^{M-1} w_j x_j \tag{3.1}
$$
で線形回帰(linear regression)と呼ばれる。モデルのパラメータ数は$w_0$から$w_{M-1}$までの$M$である。このモデルは入力変数$x_i$に関して線形になっているため表現能力が乏しい(例えば、1章の多項式曲線フィッティングで出たようなサイン曲線は線形回帰では表現できない!)。そこで、入力変数に対して非線形な関数の線形結合を考えよう。
$$
y(x, w) = w_0 + \sum_{j=1}^{M-1} w_j \phi_j(x) \tag{3.2}
$$
ただし、$ \phi_j(x) $は基底関数(basis function)とよぶ。このように非線形な基底関数を用いても、この関数はパラメータ$w$に関しては線形なので線形モデルとよぶ。
ここで入力$x$が1次元とし、$ \phi_j(x) = x^j$と定義すれば、式(3.2)は1章の多項式曲線フィッティングの式(1.1)と等価になっていることが分かる。
$$
y(x, w) = w_0 + w_1 x + w_2 x^2 + \cdots + w_M x^M \tag{1.1}
$$
基底関数$ \phi_j(x) $は何らかの前処理や特徴抽出を経て得られた特徴量と考えてもよい。
さて、式(3.2)のようにシグマの外に$w_0$(バイアスと呼ばれる)を出すと扱いにくいので、$ \phi_0(x) = 1 $と約束して以下のように書くことが多い。
$$
y(x, w) = \sum_{j=0}^{M-1} w_j \phi_j(x) = w^T \phi (x) \tag{3.3}
$$
ただし、$w = (w_0, \cdots, w_{M-1} )^T, \phi = ( \phi_0, \cdots, \phi_{M-1} ) $。
なお、1次元の入力$x$に対する基底関数$ \phi_j(x) = x^j$以外にもたくさんの選択肢がある。代表的なものは:
- ガウス基底関数(RBF1カーネル)
$$
\phi_j (x) = \exp \left\{ - \frac{( x - \mu_j)^2 }{ 2 s^2 } \right\} \tag{3.4}
$$ - シグモイド基底関数
$$
\phi_j (x) = \sigma \left( \frac{x - \mu_j}{s} \right) \tag{3.5}
$$
ただし、$ \sigma( \cdot )$はロジスティックシグモイド関数(単にシグモイド関数と呼ばれることの方が多い)と呼ばれ、
$$
\sigma(a) = \frac{1}{1 + \exp{ (-a) } }
$$
で定義される。
...とここまで基底関数な話をしてきたが、これから示すほとんどの事項は基底関数の選択に依存しないので、3章では基底関数は入力そのもの($\phi(x) = x$)と考えても問題ない(らしい)。
3.1.1 最尤推定と最小二乗法
目標変数$t$はある関数$y(x, w)$に期待値0、分散$ \beta^{-1} $なるガウスノイズが加わってできたものと考えよう。すると、$t$は観測値$x$、関数の重みパラメータ$w$、ガウスノイズのパラメータ$ \beta $が与えられた条件での確率変数と見なせるので
$$
p(t | x, w, \beta ) = N(t | y(x,w), \beta^{-1} ) \tag{3.8}
$$
と書ける。
N個の観測値$ X = \{ x_1, \cdots, x_N \} $が与えられた際の尤度関数($X, w, \beta$を固定したときに目標変数が観測される確率)は
$$
p( t | X, w, \beta) = \prod_{n=1}^N N (t_n | w^T \phi(x_n), \beta^{-1} ) \tag{3.10}
$$
となる。ガウス分布は:
$$
N (t_n | w^T \phi(x_n), \beta^{-1} ) = \left( \frac{\beta}{2 \pi} \right)^{1/2}
\exp \left\{ - \frac{\beta}{2} \left(t_n - w^T \phi (x_n) \right)^2 \right\}
$$
となることに留意すると式(3.10)の対数をとった対数尤度は
\begin{align}
\ln p (t | X, w, \beta) &= \frac{N}{2} \ln \beta - \frac{N}{2} \ln (2 \pi )
- \beta E_D (w) \tag{3.11} \\
E_D (w) &= \frac{1}{2} \sum_{n=1}^N \{ t_n - w^T \phi (x_n) \}^2 \tag{3.12}
\end{align}
wを最尤推定する
これまでの章でさんざんやってきたように、対数尤度を最大とする$w$を求めるため、式(3.11)の$w$に関する勾配 2 =0 という方程式を解けばよい。
以下、テキストと少し違う導出をする。
式(3.11)のうち、$w$に依存しているのは$E_D (w)$の項だけなので、対数尤度関数の勾配は
$$
\nabla \ln p (t | X, w, \beta ) = \beta \sum_n \left\{ t_n - w^T \phi(x_n) \right\} \phi(x_n)
$$
「勾配=0」を解きたいので
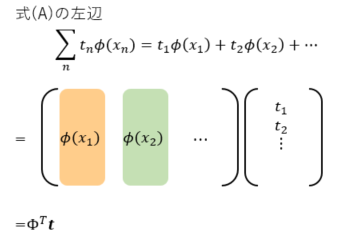
\begin{align}
\sum_n t_n \phi(x_n) &= w^T \sum_n \phi(x_n) \phi(x_n) \\
w^T \phi(x_n)はスカラーなので\phi(x_n)^T wとしても値は同じ。\\
右辺のスカラーとベクトルの積をベクトルとスカラーの積の順に書き直すと \\
\sum_n t_n \phi(x_n) &= \sum_n \phi(x_n) \phi(x_n)^T w \tag{A}
\end{align}
ここで計画行列(design matrix)と呼ばれる$\Phi$を以下のように定義する。
\begin{align}
\Phi =
\begin{pmatrix}
\phi_0(x_1) & \phi_1(x_1) & \cdots & \phi_{M-1} (x_1) \\\
\phi_0(x_2) & \phi_1(x_2) & \cdots & \phi_{M-1} (x_2) \\\
\vdots \\\
\phi_0(x_N) & \phi_1(x_N) & \cdots & \phi_{M-1} (x_N) \\\
\end{pmatrix}
=
\begin{pmatrix}
\phi(x_1)^T \\\
\phi(x_2)^T \\\
\vdots \\\
\phi(x_N)^T
\end{pmatrix}
\tag{3.16}
\end{align}
式(A)の変形をしていこう。
以上により、式(A)は
$$
\Phi^T t = \Phi^T \Phi w
$$
となるので最尤推定により得られた$w_{ML}$は
$$
w_{ML} = (\Phi^T \Phi)^{-1} \Phi^T t \tag{3.15}
$$
となる。この方程式は最小二乗問題の正規方程式 (normal equation) として知られているらしい。
また、行列$(\Phi^T \Phi)^{-1} \Phi^T$は$\Phi$の逆行列のような役割を果たすので、$\Phi$のムーア - ペンローズの擬似逆行列と呼ばれる。
バイアスパラメータw_0の役割を解釈する
バイアスパラメータを明示的に扱うことにすれば、式(3.12)の誤差関数は
$$
E_D (w) = \frac{1}{2} \sum_n \left\{ t_n - w_0 - \sum_{j=1}^{M-1} w_j \phi_j (x_n) \right\}^2 \tag{3.18}
$$
となり、$w_0$に関する微分=0 の方程式を解けば
\begin{align}
w_0 = \overline{t} - \sum_{j=1}^{M-1} w_j \overline{ \phi_j } \tag{3.19} \\
\overline{t} = \frac{1}{N} \sum_{n=1}^N t_n , \quad
\overline{ \phi_j } = \frac{1}{N} \sum_{n=1}^N \phi_j (x_n) \tag{3.20}
\end{align}
となり、バイアス$w_0$は目標値の訓練集合に対する平均$\overline{t}$と基底関数の値の平均の重み付き和$w_j \overline{ \phi_j }$との差を埋め合わせる役割をしていることが分かる。
βを最尤推定する
$w$の最尤推定と同様に、対数尤度関数である式(3.11)を$\beta$について偏微分=0 の方程式を解けばよい。$w$に関しては式(3.15)で与えられる$ w = w_{ML} $のとき対数尤度が最大になることに留意すれば、偏微分は簡単に計算出来て、以下の式が導出できる。
$$
\frac{1}{ \beta_{ML} } = \frac{1}{N} \sum_{n=1}^N \{ t_n - w_{ML}^T \phi(x_n) \}^2 \tag{3.21}
$$
3.1.2 最小二乗法の幾何学
省略。あまり理解できなかったし、この節が他の節の内容の理解にあまり役立っているとも思わないので。
3.1.3 逐次学習
式(3.15)による最尤推定は計画行列$\Phi$にすべて訓練データ$x_1, \cdots, x_N$が含まれていることから、すべての訓練データ集合を一度に推定に用いていることが分かる。
このように、すべての訓練データ集合を一度に処理する方法はバッチ手法と呼ばれる。データ数Nが大きくなると計算に時間がかかり大変という問題があるので、データ集合が大規模なときは、データ点を一度に1つだけ用いてモデルのパラメータを順次更新していく逐次学習 (sequential learning) またはオンライン学習 (on-line learning) 呼ばれるアルゴリズムを使うとよい。
逐次学習は計算量が少なくなる、記憶する必要のあるデータ量が減る(メモリを食わない)というメリットがある一方、学習結果が学習順序に依存する(最後に学習したデータの影響が大きい)というデメリットもある。
なお、深層学習 (deep learning) ではバッチ手法と逐次学習の間をとった学習法がよく行われる。1度に8~128くらいのデータ点を使ってパラメータを更新する。この手法をミニバッチ手法と呼ぶ。
逐次学習のアルゴリズムは確率的勾配降下法 (stochastic gradient descent, SGDとも) を適用して得られる。全データでの誤差関数が$ E = \sum_n E_n$のように各データのでの誤差の和となっている場合、SGDではパラメータ$w$を以下の式で更新する。
$$
w^{(\tau + 1 )} = w^{ (\tau) } - \eta \nabla E_n \tag{3.22}
$$
ただし、$\tau$は何回目のパラメータ更新かを表すインデックス、$\eta$は学習率と呼ばれる。
図を使ってこの式の解釈をしよう。
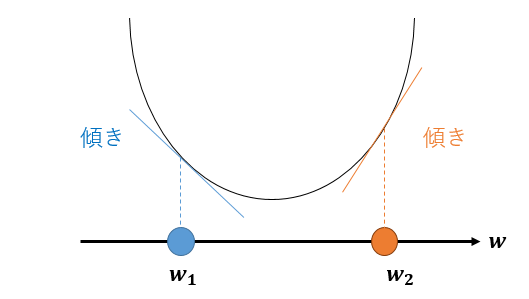
いま、誤差関数は上図の二次曲線で与えられているとし、誤差関数が最小となるような$w$を求めたい。ただし、我々は関数の形は分かっていない(どの$w$が最適解か分からない)と状況だと考えよう。
どの$w$が最適解か分からないので、とりあえず$w$をランダムに決めて$w_1$としよう。$w_1$は誤差最小となる最適解ではないので、$w_1$における傾きは0ではない。$w_1$より大きな値(右側)の方が誤差が小さくなるとき、図より誤差関数を$w$で微分した傾きは負になることが分かる。
一方、$w_2$のように、$w_2$より小さな値(左側)の方が誤差が小さくなる時、誤差関数を$w$で微分した傾きは正になることが分かる。
つまり、誤差を小さくするために
- $w$を大きくなる側に修正するべきであるときは、傾きが負
- $w$を小さくなる側に修正するべきであるときは、傾きが正
である。これを式で表現したものが式(3.22)であり、学習率$\eta$は「どれぐらいパラメータを大きく修正するか」を制御するハイパーパラメータである。
1つのデータ点での誤差が二乗和誤差関数
$$
E_n (w) = \frac{1}{2} \{ t_n - w^T \phi(x_n) \}^2
$$
で与えられているとき、$w$に関する勾配は
$$
\nabla E_n (w) = \{ t_n - w^T \phi(x_n) \} \phi(x_n)
$$
となるので、式(3.22)の更新式は
$$
w^{ (\tau+1) } = w^{ (\tau) } + \eta \{ t_n - w^{ (\tau)T } \phi (x_n) \} \phi (x_n) \tag{3.23}
$$
と書ける。