探索・推論
探索木
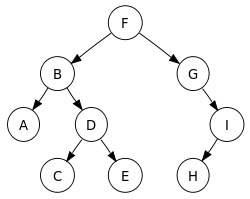
起点からスタートして，分岐点で場合分けしていき，目的の条件までたどり着くまで探索するアルゴリズム，木のような構造（ツリー構造）になることから探索木と呼ばれている．
探索にかかる時間は探索する方法によって変わる．
基本的な方法として，幅優先探索と深さ優先探索がある．
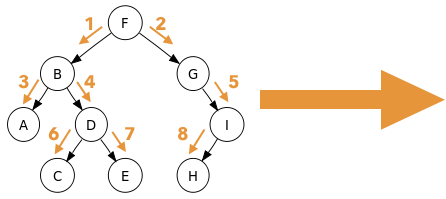
・幅優先探索
同じ層のとなりのノードを探索したあとに，下の層に進む．（横を探索）
最短距離でゴールにたどり着く経路（解）を見つけることはできるが，全てのノードに立ち寄るため，複雑になるとメモリ不足で処理できなくなる．
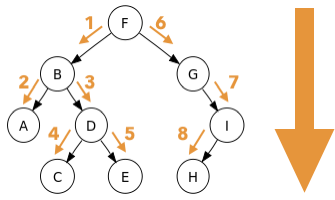
・深さ優先探索
行き止まりのノードにたどり着くまで下の層に進む．（縦を探索）
行き止まりにたどり着いたら1つ手前のノードに戻って次の行き止まりまで探索．というのを繰り返す．
1つ手前のノードに戻って探索し直せばよため，メモリ不足は心配しなくても良いが，ゴールへの経路が最短距離であるとは限らない．
また，場合によっては解を見つけるのに時間がかかってしまう．
ロボットの行動計画
ロボットの行動計画も探索を利用して作成でき，これをプランニングと呼ぶ．
例）
＜前提条件＞ロボットはRoom1にいる状態
＜行動＞右に移動
＜結果＞ロボットはRoom2にいる状態
ロボットの状態＜前提条件＞，ロボットが行う行動＜行動＞，ロボットが行動を起こした結果生じるロボットの状態＜結果＞の3つの組み合わせで記述するSTRIPS（Stanford Research Institute Problem Solver）が有名．
このプランニングを利用したもので，1970年にスタンフォード大学のテリー・ウィノグラードによって開発されたSHRDLUというシステムが有名．
※画像をクリックするとyoutubeにupされている動画を見ることができます．
ボードゲーム
2016年3月9日にDeepMind社が開発したAlphaGoが囲碁の世界でトップレベルの韓国のプロ棋士に4勝1敗で勝ち越したのは歴史的なニュース．
・コスト
効率よく探索するためにコストの概念が重要．
例えば，ある目的地へ移動する際にどの経路でどの交通手段を使うかによって，時間や費用といったコストが変わってくる．
このような場合において，あらかじめ知っている知識や経験を利用して計算すれば，少ないコストで目的を達成できる．
このような経験的知識をヒューリスティックな知識と呼ぶ．
ヒューリスティックには経験的なという意味があるが，ここでは，単に経験的という意味だけでなく，探索を効率化するのに有効なという意味を含んでいる．
人工知能で扱う問題は組み合わせの数が大きすぎえて網羅的な探索では話にならないことが多いため，ヒューリスティックな知識の利用が重要．
また，ヒューリスティックな知識を利用することで，不完全な情報でも探索や推論を進めることができる．
Mini-Max法
自分が指す時にスコアが最大（有利）になり，相手が指す時にスコアが最小になるように戦略を立てる手法．
・$αβ$法
Mini-Max法による探索を少なくする手法
最大のスコアを選択する過程でスコアが小さいノードが出現したら，そのノードを探索対象から除外することを$β$カット，最小のスコアを選択する過程ですでに出現したスコアより大きいノードが出現したら，そのノードを探索対象から除外することを$α$カットと呼ぶ．
モンテカルロ法
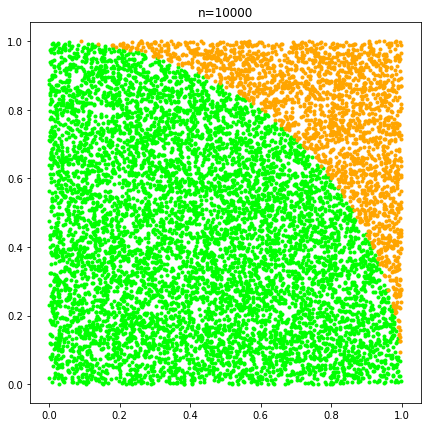
モンテカルロ法は僕の理解としては，乱数を発生させて確率やある数値（円周率など）を近似する手法です．
ここでは，ゲームがある局面まで進むと，スコア評価を放棄し，プレイアウト（ゲームを終局させること）までランダムにゲームを進めるシミュレーションを複数回実行し，どの方法が一番勝率が高いかを計算する手法．
つまり，勝率が一番高い手を探索的に探すのではなく，乱数での近似により決定する，ということを行うわけですね．
pythonでモンテカルロ法を使って円周率を近似してみました