3次元のnp.arrayのイメージがつかん、np.newaxisとは何ぞや、という疑問から自分なりの理解を書き留めた記事です。np.arrayのイメージやnp.newaxisの基本的なところを書いた前半の記事はこちら。
この記事では、np.newaxisの使いどころについて。具体的には、前半の記事で最初に述べた、2次元ベクトルを複数並べた2次元配列が2つあったときに両者に含まれるベクトル間の距離の二乗を総当たりで求める計算をやってみます。
STEP 3. ブロードキャスト
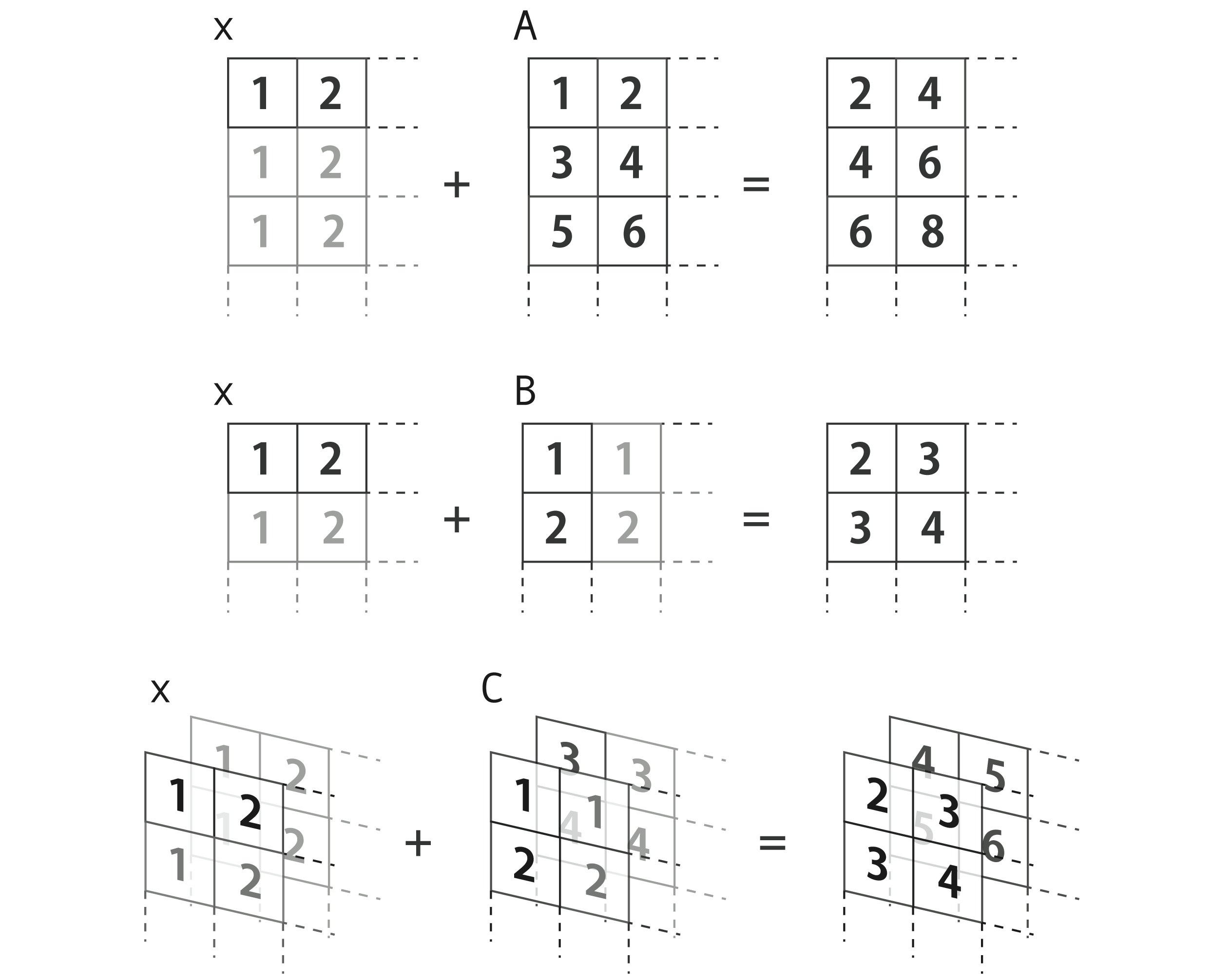
本題に入る前に、ブロードキャストについておさらい。形が違う配列同士の演算を忖度してやってくれるやつです。
>>> x = np.array([1, 2]) # よこ2たて1のベクトル
>>> A = np.array([[1, 2],
[3, 4],
[5, 6]]) # よこ2たて3の行列
>>> B = np.array([[1],
[2]]) # よこ1たて2の行列
>>> C = np.array([[[1],
[2]],
[[3],
[4]]]) # よこ1たて2奥行き2の3次元配列
>>> x + A # よこ2たて3の行列になる
array([[2, 4],
[4, 6],
[6, 8]])
>>> x + B # よこ2たて2の行列になる
array([[2, 3],
[3, 4]])
>>> x + C # よこ2たて2奥行き2の3次元配列になる
array([[[2, 3],
[3, 4]],
[[4, 5],
[5, 6]]])
STEP 4. 次元を上げてブロードキャスト演算
本題に戻って、np.newaxisって何がうれしいの?っていう話です。
一次元配列の場合
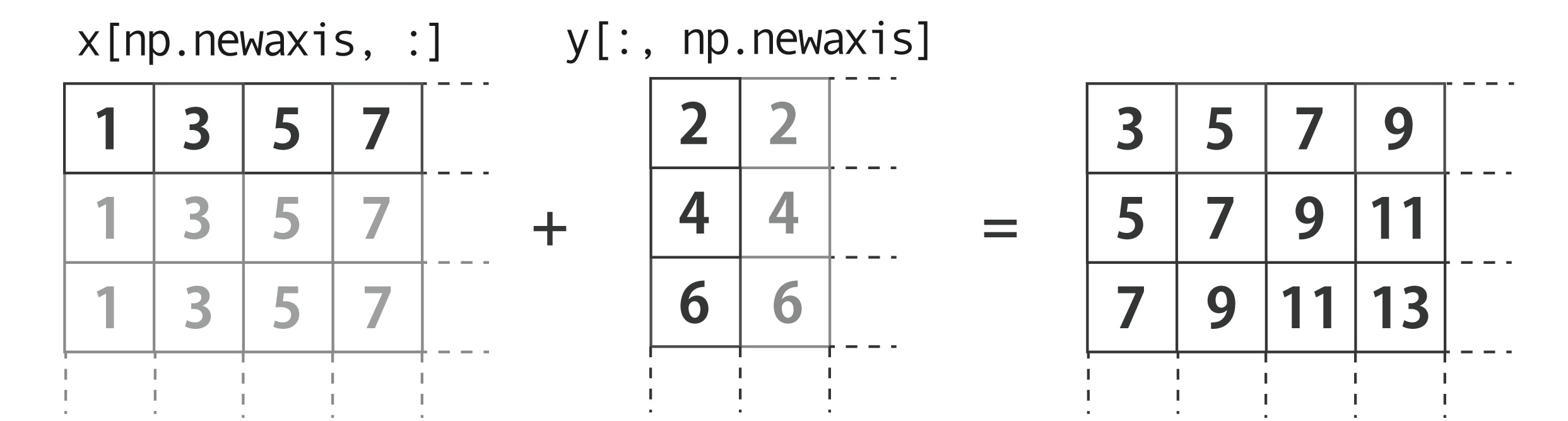
手始めに一次元配列で考えると、「2つの配列の各要素同士の総当たり演算結果を新しい軸に格納する」ためにnp.newaxisが使えるっていうところでしょうか。
例えば$x=[1, 3, 5, 7]$と$y=[2, 4, 6]$があって$4\times3=12$通りの総当たり計算をしたいとき、np.newaxisで$y$をたて3よこ1の行列に変換してから$x$と演算すれば、たて3よこ4の行列がブロードキャストによって得られる訳です。
>>> x = np.array([1, 3, 5, 7])
>>> y = np.array([2, 4, 6])
>>> x[np.newaxis, :] + y[:, np.newaxis] # xの要素とyの要素の総当たりで足し算する
array([[ 3, 5, 7, 9],
[ 5, 7, 9, 11],
[ 7, 9, 11, 13]])
# x + y[:, np.newaxis] でも同じ
二次元配列の場合
では二次元の場合どうなるでしょうか?
以下のように同じ次元の横ベクトル(ここでは2次元)が縦に並んだ配列が2つあるとします。
>>> A = np.array([[1, 2],
[3, 4],
[5, 6]])
>>> B = np.array([[1, 1],
[2, 2]])
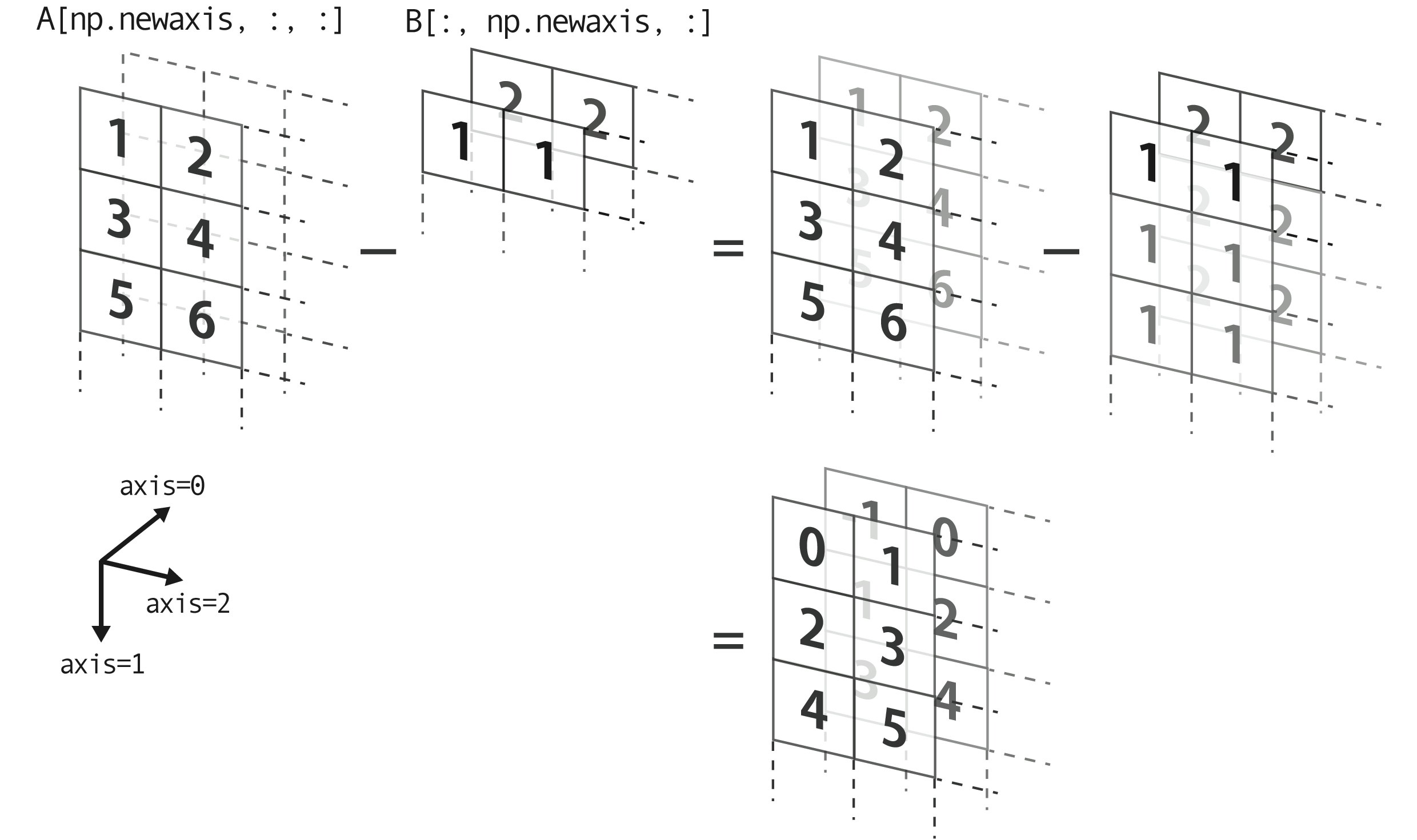
このとき、うまい具合にnp.newaxisを導入してやれば、ベクトルの各成分それぞれについて、総当たり演算ができます。一次元配列の総当たり演算を同時に複数回やるイメージ(上だと$x$成分と$y$成分)。
>>> A[np.newaxis, :, :] - B[:, np.newaxis, :] # x成分とy成分の総当たり引き算
array([[[ 0, 1],
[ 2, 3],
[ 4, 5]],
[[[-1, 0],
[ 1, 2],
[ 3, 4]]])
# A - B[:, np.newaxis, :] でも同じ
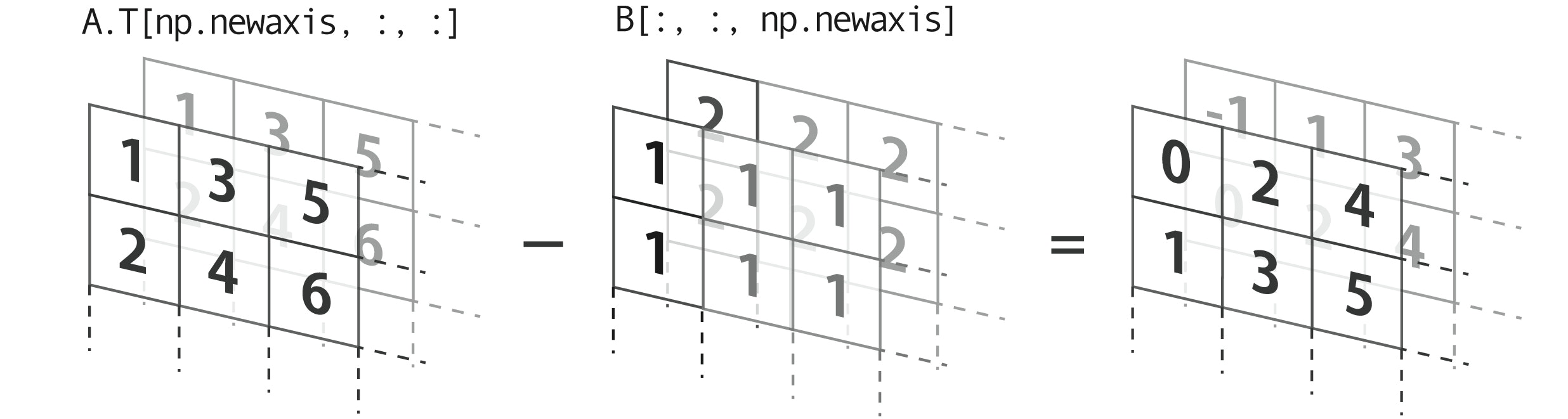
きちんとブロードキャストしてくれるように揃えれば、newaxisの取り方を変えても同じ値を得ることができます。
>>> A.T[np.newaxis, :, :] - B[:, :, np.newaxis] # x成分とy成分の総当たり引き算
array([[[ 0, 2, 4],
[ 1, 3, 5]],
[[[-1, 1, 3],
[ 0, 2, 4]]])
# A.T - B[:, :, np.newaxis] でも同じ
本題
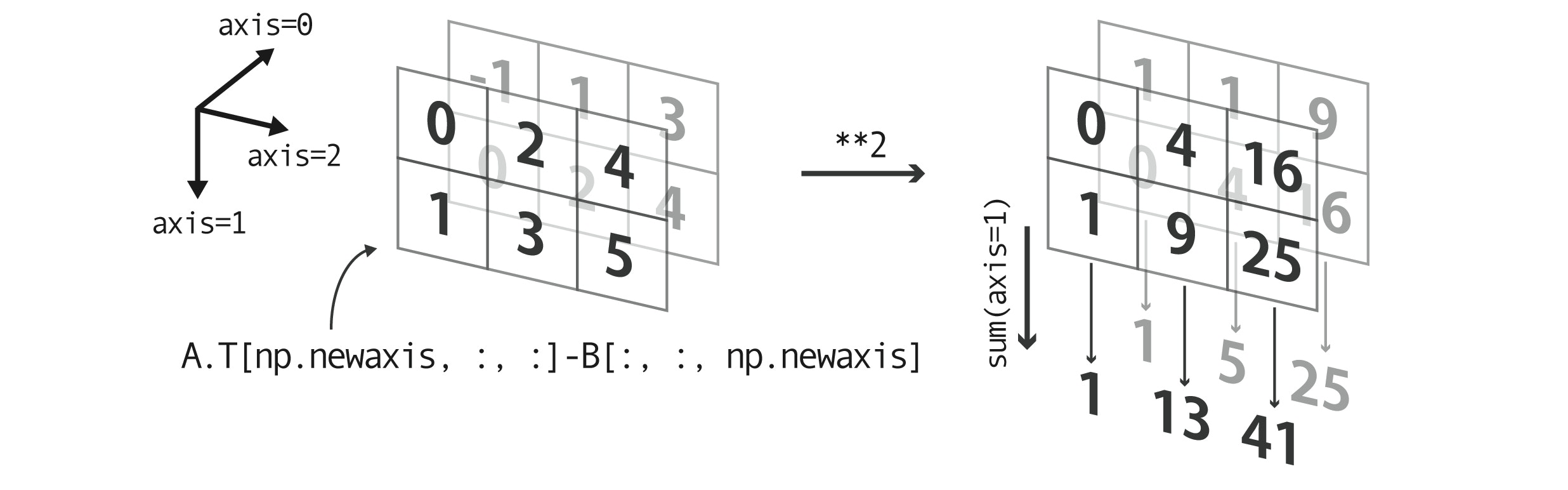
上の2次元ベクトルの組$A$と$B$があったとき、(ベクトル間距離)$^2$を総当たりで求めましょう。
$(a_x, a_y)$と$(b_x, b_y)$の距離の二乗は $(a_x-b_x)^2+(a_y-b_y)^2$ なので、まず$x$成分同士、$y$成分同士の引き算の二乗を総当たりにやればよく、それはまさしく上でやった計算を二乗するだけです。そのあと、$x$成分の差の二乗と$y$成分の差の二乗を足す= 新しい軸として$A$にも$B$にも追加していない3つ目の軸でsumしてやれば良いです(絵でイメージした方がわかりやすい)。
>>> ((A.T[np.newaxis, :, :] - B[:, :, np.newaxis])**2).sum(axis=1)
array([[ 1, 13, 41],
[ 1, 5, 25]])
# ((A.T - B[:, :, np.newaxis])**2).sum(axis=1) でもよい
これは前回の一番最初に『機械学習のエッセンス』から抜粋してきた式と等価です。
また上で見たように、$A$や$B$に追加するnewaxisの場所は一意ではなく、以下のようにしても同じ結果が得られます。
>>> ((A[np.newaxis, :, :] - B[:, np.newaxis, :])**2).sum(axis=2)
array([[ 1, 13, 41],
[ 1, 5, 25]])
# ((A - B[:, np.newaxis, :])**2).sum(axis=2) でもOK
>>> ((A.T[:, np.newaxis, :] - B.T[:, :, np.newaxis])**2).sum(axis=0)
array([[ 1, 13, 41],
[ 1, 5, 25]])
ベクトル間距離を求めるには、これの平方根を取ればいいです。