量子の重ね合わせを使って、任意の確率分布を表現する Initializer を実装する

IBM の qiskit には量子ビットを与えられた確率振幅で初期化する機能 Initializer が用意されています。
これを利用することで、量子の重ね合わせを使って、任意の確率分布を表現することができます。

この実装 (initializer.py) と元となった論文 (Synthesis of Quantum Logic Circuits) について、詳しく調べてみました。

最終的な解

簡単にするため、$ a_1, \cdots ,a_8 $ の8個の値を3個の量子ビットの重ね合わせを使って表現する場合を考えます。

各ビットに対してアダマール変換を行った状態 $ |\psi \rangle$ 、
及び、次のような演算子 $U$ を用意することができれば任意の確率分布を表現できるはずです。

U = \begin{pmatrix}
    a_1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
    0 & a_2 & 0 & 0 & 0 & 0 & 0 & 0 \\
    0 & 0 & a_3 & 0 & 0 & 0 & 0 & 0 \\
    0 & 0 & 0 & a_4 & 0 & 0 & 0 & 0 \\
    0 & 0 & 0 & 0 & a_5 & 0 & 0 & 0 \\
    0 & 0 & 0 & 0 & 0 & a_6 & 0 & 0 \\
    0 & 0 & 0 & 0 & 0 & 0 & a_7 & 0 \\
    0 & 0 & 0 & 0 & 0 & 0 & 0 & a_8
    \end{pmatrix}
    , |\psi \rangle = \frac{1}{2 \sqrt{2}} \begin{pmatrix}
    1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1
    \end{pmatrix}
    , U |\psi \rangle = \frac{1}{2 \sqrt{2}} \begin{pmatrix}
    a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ a_6 \\ a_7 \\ a_8
    \end{pmatrix}

ただし、 $ |a_1|^2 + |a_2|^2 + \cdots + |a_8|^2 = 1 $

この $U$ を分解していくことで、具体的な実装を導出します。

量子ビットの回転

任意の状態 $ |\psi \rangle $ は $z$ 軸回転と $y$ 軸回転を順に行うことによって、$ |0 \rangle $ にすることができます。

R_y(\theta) R_z(\phi) |\psi \rangle = r |0 \rangle

R_y(\theta) = \begin{pmatrix}
\cos{\theta/2} & \sin{\theta/2} \\
-\sin{\theta/2} & \cos{\theta/2}
\end{pmatrix}
, R_z(\phi) = \begin{pmatrix}
e^{-i \phi /2} & 0 \\
0 & e^{i \phi /2}
\end{pmatrix}

$r$ は正規化定数になります。initializer.py では _bloch_angles メソッドで回転角を求めています。
試しに

 |\psi \rangle = \begin{pmatrix} 0.5 \\ -0.2 \end{pmatrix}

で計算してみます。

from qiskit.extensions import Initialize

psi = [0.5, -0.2]
(r, theta, phi) = Initialize._bloch_angles(psi)
print("theta=", theta, " phi=", phi)

theta= 0.7610127542247305  phi= 3.141592653589793

求められた $ \theta, \phi $ で回転させてみると、確かに $|0 \rangle $ に一致します。（グローバルな位相は無視）

import sympy

Rz = sympy.Matrix([
[sympy.exp(-phi/2*sympy.I), 0],
[0, sympy.exp(phi/2*sympy.I)]
])

Ry = sympy.Matrix([
[sympy.cos(theta/2), sympy.sin(theta/2)],
[-sympy.sin(theta/2), sympy.cos(theta/2)]
])

x = Ry * Rz * sympy.Matrix(psi) / r
print(sympy.re(x[0]), sympy.im(x[0]))
print(sympy.re(x[1]), sympy.im(x[1]))

-1.00000000000000 -1.05572999926496e-16
2.87126644299609e-16 4.22291999705984e-17

回転行列によるエンタングルメントの解除(disentangle)

$U |\psi \rangle$ を4個の2次元ベクトルに分解します。

|\psi_1 \rangle = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix},
|\psi_2 \rangle = \begin{pmatrix} a_3 \\ a_4 \end{pmatrix},
|\psi_3 \rangle = \begin{pmatrix} a_5 \\ a_6 \end{pmatrix},
|\psi_4 \rangle = \begin{pmatrix} a_7 \\ a_8 \end{pmatrix}

$|\psi_1 \rangle$ を $|0 \rangle$ に移す回転行列 $ R_1 $ を前節の要領で求めて、$ R_1 |\psi_1 \rangle = r_1 |0 \rangle $ となるようにします。
同様に、$|\psi_2 \rangle, |\psi_3 \rangle, |\psi_4 \rangle$ を $|0 \rangle$ に移す回転行列 $ R_2, R_3, R_4$ と定数 $ r_2, r_3, r_4 $ を適切に決めます。

回転行列 $ R_1, R_2, R_3, R_4 $ を使って、$ U |\psi \rangle $ を次のように変形します。

\begin{pmatrix}
R_1 &  &  & \\
& R_2 & & \\
& & R_3 & \\
& & & R_4
\end{pmatrix}
U |\psi \rangle =
\frac{1}{2 \sqrt{2}}
\begin{pmatrix}
R_1 |\psi_1 \rangle \\ R_2 |\psi_2 \rangle \\ R_3 |\psi_3 \rangle \\ R_4 |\psi_4 \rangle
\end{pmatrix}
= \begin{pmatrix}
r_1 |0 \rangle \\ r_2 |0 \rangle \\ r_3 |0 \rangle \\ r_4 |0 \rangle
\end{pmatrix}
= \begin{pmatrix}
r_1 \\ r_2 \\ r_3 \\ r_4
\end{pmatrix}
\otimes |0 \rangle

上式の最後の表記を見ると、4次元ベクトル(=2量子ビット)と $|0 \rangle$ のテンソル積になっています。
つまり、1量子ビットのエンタングルメントを解除できたことになります。
残りの

\begin{pmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \end{pmatrix}

について同様にエンタングルメント解除を行うことで、すべての量子ビット間のエンタングルメントを取り除くことができます。

initializer.py では gates_to_uncompute メソッドで実装されています。

マルチプレクサの実装

回転演算子を対角に並べた行列

 \begin{pmatrix} R_1 &  &  & \\ & R_2 & & \\ & & R_3 & \\ & & & R_4 \end{pmatrix}

は $ R_1 \oplus R_2 \oplus R_3 \oplus R_4 $ と表記されます。この $ \oplus $ 演算をマルチプレクサと呼ぶようです。

論文によれば、$ R_1 = R(\phi_1), R_2 =R(\phi_2) $ の両方がy軸回転、またはz軸回転の場合にマルチプレクサ $ R(\phi_1) \oplus R(\phi_2) $ を実装すると次のような量子回路になります。

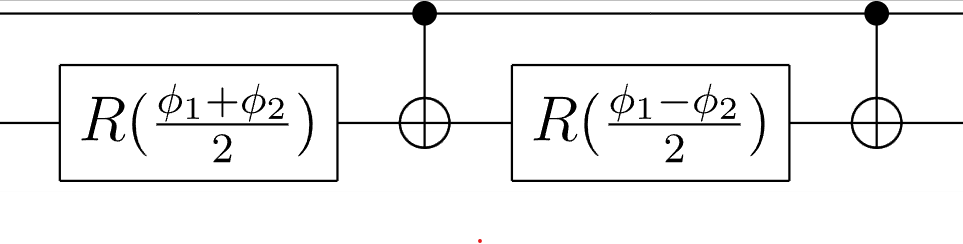
$ R_1 \oplus R_2 \oplus R_3 \oplus R_4 $ の実装を考える場合、

R(\phi_1, \phi_2) = \begin{pmatrix} R(\phi_1) & \\ & R(\phi_2) \end{pmatrix} ,
R(\phi_3, \phi_4) = \begin{pmatrix} R(\phi_3) & \\ & R(\phi_4) \end{pmatrix}

と置いて、
$ R(\phi_1, \phi_2) \oplus R(\phi_3, \phi_4) $ の量子回路を考えます。

initializer.py では _multiplex メソッドで実装されています。
メソッド内で回転演算子を2つに分割し、_multiplex メソッドを再帰的に呼び出しています。
さらに、上の図の回路の順序を逆にしても結果が変わらないことを利用して、連続するCNOTゲートを作り出すことで最適化を行っています。

$ R_z(\phi_1) \oplus R_z(\phi_2) $ の場合について、sympy で確かめてみます。

phi_1 = sympy.Symbol('phi_1')
phi_2 = sympy.Symbol('phi_2')

# $RZ_1 = I \otimes R_z((\phi_1 + \phi_2)/2) $
RZ_1 = sympy.Matrix([
[sympy.exp(-(phi_1+phi_2)/4*sympy.I), 0, 0, 0],
[0, sympy.exp((phi_1+phi_2)/4*sympy.I), 0, 0],
[0, 0, sympy.exp(-(phi_1+phi_2)/4*sympy.I), 0],
[0, 0, 0, sympy.exp((phi_1+phi_2)/4*sympy.I)]
])

# $RZ_2 = I \otimes R_z((\phi_1 - \phi_2)/2) $
RZ_2 = sympy.Matrix([
[sympy.exp(-(phi_1-phi_2)/4*sympy.I), 0, 0, 0],
[0, sympy.exp((phi_1-phi_2)/4*sympy.I), 0, 0],
[0, 0, sympy.exp(-(phi_1-phi_2)/4*sympy.I), 0],
[0, 0, 0, sympy.exp((phi_1-phi_2)/4*sympy.I)]
])

CX = sympy.Matrix([
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 0, 1],
[0, 0, 1, 0]
])

CX * RZ_2 * CX * RZ_1

 \left[\begin{matrix}e^{i \left(- \frac{\phi_{1}}{4} - \frac{\phi_{2}}{4}\right)} e^{i \left(- \frac{\phi_{1}}{4} + \frac{\phi_{2}}{4}\right)} & 0 & 0 & 0\\0 & e^{i \left(\frac{\phi_{1}}{4} - \frac{\phi_{2}}{4}\right)} e^{i \left(\frac{\phi_{1}}{4} + \frac{\phi_{2}}{4}\right)} & 0 & 0\\0 & 0 & e^{i \left(- \frac{\phi_{1}}{4} - \frac{\phi_{2}}{4}\right)} e^{i \left(\frac{\phi_{1}}{4} - \frac{\phi_{2}}{4}\right)} & 0\\0 & 0 & 0 & e^{i \left(- \frac{\phi_{1}}{4} + \frac{\phi_{2}}{4}\right)} e^{i \left(\frac{\phi_{1}}{4} + \frac{\phi_{2}}{4}\right)}\end{matrix}\right]

この結果より、確かにマルチプレクサになっていることが分かりました。

= \begin{pmatrix}
e^{-i \phi_1 /2} & 0 & 0 & 0 \\
0 & e^{i \phi_1 /2} & 0 & 0 \\
0 & 0 & e^{-i \phi_2 /2} & 0 \\
0 & 0 & 0 & e^{i \phi_2 /2}
\end{pmatrix}
= R_z(\phi_1) \oplus R_z(\phi_2)

$ R_y(\theta_1) \oplus R_y(\theta_2) $ についても計算します。

theta_1 = sympy.Symbol('theta_1')
theta_2 = sympy.Symbol('theta_2')

RY_1 = sympy.Matrix([
[sympy.cos((theta_1+theta_2)/4), sympy.sin((theta_1+theta_2)/4), 0, 0],
[-sympy.sin((theta_1+theta_2)/4), sympy.cos((theta_1+theta_2)/4), 0, 0],
[0, 0, sympy.cos((theta_1+theta_2)/4), sympy.sin((theta_1+theta_2)/4)],
[0, 0, -sympy.sin((theta_1+theta_2)/4), sympy.cos((theta_1+theta_2)/4)]
])
RY_2 = sympy.Matrix([
[sympy.cos((theta_1-theta_2)/4), sympy.sin((theta_1-theta_2)/4), 0, 0],
[-sympy.sin((theta_1-theta_2)/4), sympy.cos((theta_1-theta_2)/4), 0, 0],
[0, 0, sympy.cos((theta_1-theta_2)/4), sympy.sin((theta_1-theta_2)/4)],
[0, 0, -sympy.sin((theta_1-theta_2)/4), sympy.cos((theta_1-theta_2)/4)]
])

CX * RY_2 * CX * RY_1

\left[\begin{matrix}- \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} + \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} & \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} + \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} & 0 & 0\\- \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} - \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} & - \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} + \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} & 0 & 0\\0 & 0 & \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} + \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} & - \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} + \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)}\\0 & 0 & \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} - \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} & \sin{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \sin{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)} + \cos{\left(\frac{\theta_{1}}{4} - \frac{\theta_{2}}{4} \right)} \cos{\left(\frac{\theta_{1}}{4} + \frac{\theta_{2}}{4} \right)}\end{matrix}\right]

= \begin{pmatrix}
\cos{\theta_1 /2} & \sin{\theta_1 /2} & 0 & 0 \\
-\sin{\theta_1 /2} & \cos{\theta_1 /2} & 0 & 0 \\
0 & 0 & \cos{\theta_2 /2} & \sin{\theta_2 /2} \\
0 & 0 & -\sin{\theta_2 /2} & \cos{\theta_2 /2}
\end{pmatrix}
= R_y(\theta_1) \oplus R_y(\theta_2)

ついでに、順序を逆に入れ替えても同じであることを確認します。

CX * RY_2 * CX * RY_1 == RY_1 * CX * RY_2 * CX

True

仕上げ

マルチプレクサを使って1ビットずつエンタングルメントを解除していくことで、
$ U |\psi \rangle $ を $ |000 \rangle $ に変換させる量子回路を求めることができました。
これの逆(inverse)を行う回路が、当初求めたかった任意の確率分布を表現する回路になります。

実際に qiskit で NormalDistribution ライブラリを呼び出して、正規分布を表現する回路の中を確認します。
(NormalDistribution の中で initialiser が呼び出されています。)

量子回路を inverse して表示させてみると、q_0 を disentangle するマルチプレクサ、q_1 を disentangle するマルチプレクサ、
q_2 を回転するゲートで構成されていることが分かります。

#from qiskit_finance.circuit.library import NormalDistribution
from qiskit.circuit.library import NormalDistribution
%config InlineBackend.figure_formats = ['svg']

# Normal Distribution
num_qubits = 3
high = 3
low = -1
mu = 1.0
sigma = 0.5 # sigmaに格納する値は標準偏差ではなく分散

normal = NormalDistribution(num_qubits, mu=mu, sigma=sigma, bounds=(low, high))
normal.inverse().decompose().draw(output='mpl')

さらに分解していくと、マルチプレクサを再帰呼び出しする部分が見えてきます。

normal.inverse().decompose().decompose().draw(output='mpl')

normal.inverse().decompose().decompose().decompose().draw(output='mpl')

問題点

このアルゴリズムでは $n$ 量子ビットの initializer 回路において $ 2^{n+1} - 2n - 2 $ 個の CNOT ゲートが必要になります。
（最適化の効果で実際には少し減らすことができ、3量子ビットの場合には6個の CNOT ゲートを使用します。）

これでは現状のノイズが多い量子コンピュータを使うとき、数ビット程度でしか動かすことができなくなってしまうので、
より効率的なアルゴリズムを模索する必要があります。

参考

• Vivek V. Shende, Stephen S. Bullock, Igor L. Markov
  Synthesis of Quantum Logic Circuits
  (arXiv:quant-ph/0406176)

• Qiskit Initializer
  https://qiskit.org/documentation/stubs/qiskit.extensions.Initialize.html