$\def\bra#1{\mathinner{\left\langle{#1}\right|}}\def\ket#1{\mathinner{\left|{#1}\right\rangle}}\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}$
振り返り
以前に「量子の重ね合わせを使って、任意の確率分布を表現する Initializer を実装する」にて、量子ビットを使ってデータを表現する手法を実験しました。
この Initializer は以下のような性質があります。残念ながら欠点が致命的で、限られた用途でしか使用できません。将来的にも実用性を見出すことは困難です。
- 特長
- 正確なデータを表現できる
- 必要な量子ビット数はデータ量に対して対数のオーダーでよい
- 欠点
- 必要な量子ゲート数が量子ビット数に対して指数のオーダーになる
Approximate Amplitude Encoding (AAE) を使用したデータ表現
今回はパラメータ付き量子回路 (PQC) を使用することで、必要な量子ゲート数を削減した Approximate Amplitude Encoding (AAE) と呼ばれる方法を試してみます。
こちらの方法は以下の性質があります。詳細は別途考察します。
- 特長
- 必要な量子ビット数はデータ量に対して対数のオーダーでよい (Initializer と同じ)
- 必要な量子ゲート数は量子ビット数に対して多項式オーダーでよい
- 欠点
- データを近似表現する手法である。近似精度をコントロールできないので、実用的に使えない可能性がある。
このように、データを近似表現する代わりに必要な量子ゲート数が少なくてよいアルゴリズムになっています。
果たして、AAE はどれくらい実用に耐えうるのでしょうか。
問題設定
$|a_0|^2 + |a_1|^2 + \cdots + |a_{n-1}|^2 = 1$ となる条件で、$a_0$ 〜 $a_{n-1}$ の $n$ 個の値を $\log n$ 個の量子ビットで表現します。
例えば、$n=8$ のとき、
$\ket{\psi} = a_0 \ket{000} + a_1 \ket{001} + a_2 \ket{010} + a_3 \ket{011} + a_4 \ket{100} + a_5 \ket{101} + a_6 \ket{110} + a_7 \ket{111}$
なる状態を作り出す量子回路を考えます。
Initializer には $a_0, \cdots, a_{n-1} \ge 0$ の制約がありましたが、AAE では補助ビットを1個用意することで負の値も表現できるため、そのような制約はありません。
量子回路
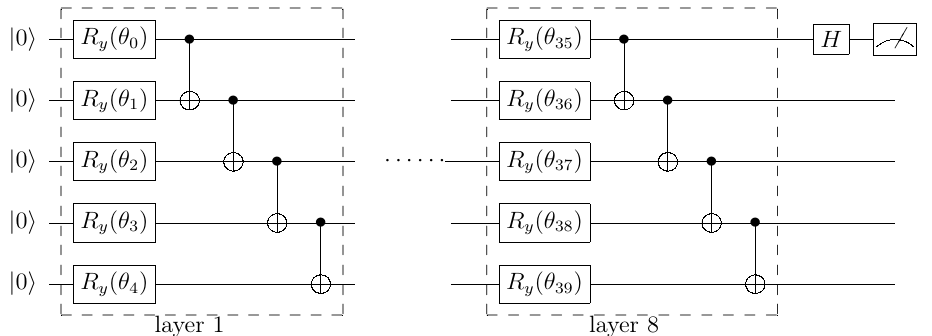
4 量子ビットと 1 個の補助ビットで 16 個のデータを表現する量子回路は次のようになります。
Ry と CNOT の2種類のゲートからなる PQC を 8 層並べた $U(\theta)$ 、及び H ゲートからなっており、Ry ゲートの回転角 $\bf{\theta}$ がパラメータになっています。 $a_0, \cdots, a_{n-1}$ の値から適切なパラメータの値を決める必要があります。1番目のビットは補助ビットです。
図から明らかなように AAE に必要な量子ゲート数は $U(\theta)$ の層の数に依存します。
適切な層数は、数値精度や計算時間を考慮して実験的に決められます。
正負符号の対応
符号を考慮するために、$a_0, \cdots, a_{n-1}$ を正負のグループに分け、正の場合は補助ビットを $\ket{0}$、負の場合には補助ビットを $\ket{1}$ として符号を反転させます。
例えば、$a_0, a_3, a_5, a_6, a_7 \ge 0 \quad a_1, a_2, a_4 \lt 0$ のとき、
$\ket{\bar{\psi}} = a_0 \ket{000}\ket{0} - a_1 \ket{001}\ket{1} - a_2 \ket{010}\ket{1} + a_3 \ket{011}\ket{0} - a_4 \ket{100}\ket{1} + a_5 \ket{101}\ket{0} + a_6 \ket{110}\ket{0} + a_7 \ket{111}\ket{0}$
とすることで、$\ket{\bar{\psi}}$ の確率振幅はすべて正の実数になります。
表現したデータを後に続く計算に利用する場合、補助ビット以外のビットを使用します。
補助ビットについては、アダマール変換して観測します。
\begin{align}
& I^{\otimes n} \otimes H \ket{\bar{\psi}} \\
& = \frac{1}{\sqrt{2}} (a_0 \ket{000} - a_1 \ket{001} - a_2 \ket{010} + a_3 \ket{011} - a_4 \ket{100} + a_5 \ket{101} + a_6 \ket{110} + a_7 \ket{111}) \otimes \ket{0} \\
& + \frac{1}{\sqrt{2}} (a_0 \ket{000} + a_1 \ket{001} + a_2 \ket{010} + a_3 \ket{011} + a_4 \ket{100} + a_5 \ket{101} + a_6 \ket{110} + a_7 \ket{111}) \otimes \ket{1}
\end{align}
この式の第2項を見ると、補助ビットが $\ket{1}$ であるときに、$a_0, \cdots, a_7$ が符号付きで表現できているので、最終的に補助ビットの観測結果が $\ket{1}$ の結果のみ採用すればよいことになります。
パラメータの学習
AAE ではパラメータ $\bf{\theta}$ を求めるために機械学習と同様の手法を使ってパラメータを学習します。すなわち、$U(\bf{\theta}) \ket{0}$ と $\ket{\bar{\psi}}$ が等しくなるような $\theta$ を探索します。
ここで、$U(\bf{\theta})$ は Ry と CNOT ゲートのみ使用しているため、$a_0, \cdots, a_{n-1}$ の値は実数になります。よって以降は $a_0, \cdots, a_{n-1}$ の絶対値のみを考えます。
論文の中では、パラメータ学習において次の条件を満たせば良いことが示されています。
- $a_j$ の絶対値について、次の式を満たす。
$$
{|a_j|}^2 = | \braket{j|U(\bf{\theta})|0} |^2
$$ - $a_j$ をアダマール変換したものと、$U(\bf{\theta}) \ket{0}$ をアダマール変換したものについても同様の関係を満たす。
$$
{|a_j^H|}^2 = | \braket{j|H^{\otimes n}U(\bf{\theta})|0} |^2
$$
学習時の損失関数
パラメータの学習を行うために、損失関数を定義してその勾配を求めなければなりません。
AAE ではガウシアンカーネルを用いて、$U(\bf{\theta}) \ket{0}$ のサンプル $j$ と $\ket{\bar{\psi}}$ のサンプル $k$ の差を定式化します。そして、MMD(Maximum Mean Discrepancy) と呼ばれる指標によって、 $U(\bf{\theta}) \ket{0}$ と $\ket{\bar{\psi}}$ の分布の差を算出し、これを損失関数とします。
-
ガウシアンカーネル
$$
\kappa (j, k) = \exp{\Bigl( \frac{-|j - k|^2}{2\sigma^2} \Bigr)}
$$ -
MMD
\mathcal{L}_{MMD} (q, p) = \bf{E}_{j \sim q, k \sim q}[\kappa(j, k)]
-2 \bf{E}_{j \sim q, k \sim p}[\kappa(j, k)]
+ \bf{E}_{j \sim p, k \sim p}[\kappa(j, k)]
\\
\bf{E}_{j \sim q, k \sim q}[\kappa(j, k)] = \sum_{j=0}^{N-1} \sum_{k=0}^{N-1} \kappa(j, k) q(j) q(k)
勾配については、パラメータシフト法によって算出します。
実装
量子回路の開発には Qiskit を使用しました。
まずは必要なパッケージを読み込んで、論文中で使われている $a_0, \cdots, a_{n-1}$ の値と同じものを用意します。$a$ の二乗和はほぼ1になります。
import qiskit
from qiskit.circuit import QuantumCircuit, ParameterVector
import numpy.random as rng
import numpy as np
from scipy.linalg import hadamard
import matplotlib.pyplot as plt
import math
from scipy.optimize import minimize
import random
from qiskit import Aer, transpile
a = np.array([[ 0.34879053, -0.04607624, 0.04914744, -0.35186172],
[ 0.34859443, -0.20608682, -0.26600485, 0.12349723],
[-0.12862017, 0.0019959 , -0.27242289, 0.39904716],
[ 0.21908688, 0.25317765, -0.12127338, -0.35099115]])
print(np.sum(a**2))
0.9999999967863236
クラス ApproximateAmplitudeEncoder にて AAE の本体を実装していきます。
初期化時に、量子ビット数(num_qubits)、PQC の深さ(num_layers) 等の値をメンバ変数にセットします。計算の実行には QasmSimulator を使います。
class ApproximateAmplitudeEncoder():
def __init__(self, X, num_qubits, num_layers, shots, sigma):
self.X = X
self.num_qubits = num_qubits
self.num_layers = num_layers
# パラメータθ
self.params = np.random.rand(num_layers, self.num_qubits) * 2 * np.pi
self.data_num = self.X.shape[0]
self.shots = shots
self.sigma = sigma
self.history = []
self.backend_sim = Aer.get_backend('qasm_simulator')
PQC を作成します。
# L 番目のレイヤーの量子回路
def layer(self, r, params, L):
for i in range(self.num_qubits):
r.ry(params[L, i], i)
for i in range(self.num_qubits - 1):
r.cx(i, (i + 1))
# PQC を取得する
def get_qc(self):
qc = QuantumCircuit(self.num_qubits)
for i in range(self.num_layers):
if self.params.ndim == 1:
_params = np.reshape(self.params, (self.num_layers, -1))
else:
_params = self.params
self.layer(qc, _params, i)
return qc
$\ket{\bar{\psi}}$ からサンプリングします。
確率振幅に従って量子状態を文字列として返す関数になっています。
def random_from_dataset(self):
element_list = range(2**self.num_qubits)
samples = np.random.choice(a=element_list, size=self.shots, p=self.X**2)
# 数値列をバイナリ文字列に変換
return [np.array(list(format(s, f'0{self.num_qubits}b')), dtype=np.int64) for s in samples]
$U(\theta)\ket{0}$ からサンプリングします。
shots で指定した回数だけサンプリングした結果をランダムにシャッフルして返します。
def sample_from_qc(self, params):
qc = QuantumCircuit(self.num_qubits, self.num_qubits)
for i in range(self.num_layers):
if params.ndim == 1:
_params = np.reshape(params, (self.num_layers, -1))
else:
_params = params
self.layer(qc, _params, i)
for i in range(self.num_qubits):
qc.measure(i, i)
job_sim = self.backend_sim.run(transpile(qc, self.backend_sim), shots=self.shots)
res = job_sim.result().get_counts()
res_list = []
for item in res.items():
res_list += [np.array(list(i), dtype = np.int64) for i in [item[0]] * item[1]]
random.shuffle(res_list)
return res_list
MMD を算出します。
実際には $U(\theta) \ket{0}$ と $\ket{\psi}$ をアダマール変換したものについても MMD を計算する必要がありますが、長くなるのでコードの記述は割愛します。(実際にはアダマール変換後の計算も行っています)
def gauss_kernel(self, x, y):
if np.ndim(self.sigma) == 0:
self.sigma = np.array([self.sigma])
x = np.array(x)
y = np.array(y)
x_ = np.reshape(x, (x.shape[0], 1, x.shape[1]))
y_ = np.array([y for i in range(y.shape[0])])
d = np.sum((x_ - y_)**2, axis = 2)
K = np.mean([np.exp(-0.5 / s * d) for s in self.sigma])
return K
def SMMD_loss(self):
s = self.sample_from_qc(self.params)
p = self.random_from_dataset()
E1 = self.gauss_kernel(random.sample(s, self.shots), random.sample(s, self.shots))
E2 = -2 * self.gauss_kernel(random.sample(s, self.shots), random.sample(p, self.shots))
E3 = self.gauss_kernel(random.sample(p, self.shots), random.sample(p, self.shots))
return E1 + E2 + E3
パラメータシフト法で勾配を求めます。
def grad(self):
mask = np.eye(self.params.size) * np.pi / 2
gradient = np.zeros(self.params.size)
qc_sample = self.sample_from_qc(self.params)
qc_sample_h = self.sample_from_qc_h(self.params)
for i in range(self.params.size):
params_p = self.params + np.reshape(mask[i, :], self.params.shape)
params_m = self.params - np.reshape(mask[i, :], self.params.shape)
qc_sample_p = self.sample_from_qc(params_p)
qc_sample_m = self.sample_from_qc(params_m)
E1 = self.gauss_kernel(random.sample(qc_sample_p, self.shots), random.sample(qc_sample, self.shots))
E2 = self.gauss_kernel(random.sample(qc_sample_m, self.shots), random.sample(qc_sample, self.shots))
E3 = self.gauss_kernel(random.sample(qc_sample_p, self.shots), self.random_from_dataset())
E4 = self.gauss_kernel(random.sample(qc_sample_m, self.shots), self.random_from_dataset())
g = E1 - E2 - E3 + E4
gradient[i] = g
return np.reshape(np.array(gradient), self.params.shape)
オプティマイザを指定してパラメータを学習します。
本記事ではコードを省略しますが、Adam を使用します。
def fit(self, ite=100, optimizer=None, lr = 1e-3):
for i in range(ite):
g = self.grad()
if optimizer is None:
self.params -= g * lr # SGD
else:
optimizer.update(self.params, g)
loss = self.SMMD_loss()
self.history.append(loss)
print("iter:", i, " loss:", loss)
実験
表現したいデータ $a$ について、$\ket{\bar{\psi}}$ の形式に変換します。
data = []
for j in range(a.shape[0]):
# Data+
if a[j] >= 0:
data.append(a[j])
data.append(0)
# Data-
if a[j] < 0:
data.append(0)
data.append(-a[j])
data = np.array(data)
パラメータの学習を行います。
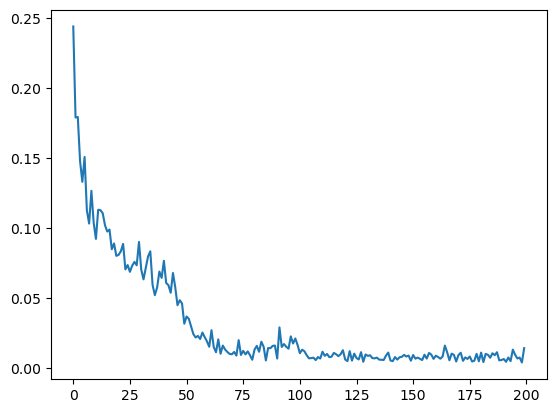
論文の記述では、学習率 0.1 で 100 iteration、0.01 でさらに 100 iteration となっていますが、MMD の値をまだ小さくできそうだったので、学習率 0.01 でさらに 200 iteration 行いました。
最後の学習率 0.01 での 200 iteration では MMD が次のように減衰しました。
model = ApproximateAmplitudeEncoder(data, n, num_layers = 8, shots = 512, sigma = [0.25])
optimizer = Adam()
optimizer.lr = 1e-1
model.fit(100, optimizer)
optimizer.lr = 1e-2
model.fit(200, optimizer)
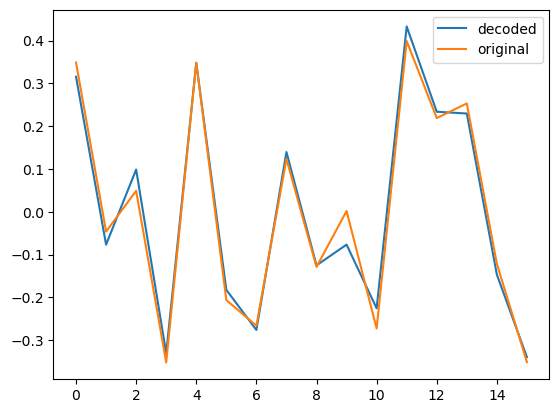
ここで学習した $\theta$ の値を使って $U(\theta) \ket{0}$ のサンプリングを行い、元の表現したかったデータを復元して、正しい値と並べてみると、次のようになりました。
グラフの横軸が $j$ で縦軸が $a_j$ 、青の実線が AAE で再現した値で橙の実線が正しい値になります。必要な表現の精度はアプリケーションによりますが、まずまず良いのではないでしょうか。
注意事項
今回の実験ではパラメータ学習時に発生しやすい、勾配消失問題への対応を行っていません。
また、コードの最適化を行っていないため、計算時間の評価は行っていません。
(CPU を 1 コアしか使っておらず、1 回の試行に 1 時間程度かかりました。)
今後の予定
Initializer よりも少ない量子ゲート数でデータ表現できることが分かりました。
この後、表現したいデータ値や量子ビット数を変えて、表現の精度が低下しやすいデータや、実用上の最大量子ビット数などを確認してみたいと思います。
参考
Kouhei Nakaji and Shumpei Uno and Yohichi Suzuki and Rudy Raymond and Tamiya Onodera and Tomoki Tanaka and Hiroyuki Tezuka and Naoki Mitsuda and Naoki Yamamoto
Approximate amplitude encoding in shallow parameterized quantum circuits and its application to financial market indicators
(arXiv:2103.13211)