はじめに
ぶっちゃけ回帰における基底関数表現の式とカーネル関数表現の式を毎回忘れるので、どこかにメモを残しておこうってことで記事を書こうと思った次第です。ただまぁ単に覚書にするのは勿体無い気がしたので、簡単な解説記事にしてみました。
覚書用
簡潔にまとめたバージョン。忙しい人もしくは私と同様に思い出したい人用
目的関数
\begin{align*}
F &= \frac{1}{2} \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) + \frac{1}{2} \mathbf{w} ^T H \mathbf{w} \\
\end{align*}
$\mathbf{y} = (y_1, \dots, y_N)^T \in \mathbb{R} ^N$:出力データ($y_n \in \mathbb{R}$)
$X = (\mathbf{x}_1, \dots, \mathbf{x}_N)^T \in \mathbb{R} ^{N \times D}$:入力データ($\mathbf{x}_n \in \mathbb{R}^D$)
$\mathbf{w} \in \mathbb{R} ^D$:パラメータ
$G \in \mathbb{R} ^{N \times N}$:データの重み(対角行列)
$H \in \mathbb{R} ^{D \times D}$:正則化項の重み(対角行列)
最適化
パラメータ
・基底関数表現
\begin{align*}
\hat{\mathbf{w}} = \left( X^T G X + H\right)^{-1}X^T G \mathbf{y} \\
\tag{1}
\end{align*}
・カーネル表現
\begin{align*}
\hat{\mathbf{w}} = H^{-1} X^T \left( X H^{-1} X^T + G^{-1} \right)^{-1} \mathbf{y} \\
\tag{2}
\end{align*}
推定値
・基底関数表現
\begin{align*}
\hat{\mathbf{y}} &= X \hat{\mathbf{w}} \\
&= X \left( X^T G X + H\right)^{-1}X^T G \mathbf{y} \\
&= X X^{\dagger} \mathbf{y} \\
\end{align*}
ただし$X^{\dagger} \triangleq \left( X^T G X + H\right)^{-1}X^T G$
・カーネル関数表現
\begin{align*}
\hat{\mathbf{y}} &= X \hat{\mathbf{w}} \\
&= X H^{-1} X^T \left( X H^{-1} X^T + G^{-1} \right)^{-1} \mathbf{y} \\
&= K \left( K + G \right)^{-1} \mathbf{y}
\end{align*}
ただし$K \triangleq X H^{-1} X^T$
解説
重み付き線形回帰の背景
本題は双対表現を得ることなので、重み付き線形回帰自体の説明はさらっとします。
まず重み付き線形回帰を一言で言うと「重み付き線形回帰はデータの信頼度がわかってる場合や特定のデータだけは誤差を小さくしたい場合とかに使える回帰手法」です。
通常の回帰では入力$\mathbf{x}_n$と出力$y_n$のペアが$N$組み与えられた時、以下のような目的関数$F$を
\begin{align*}
F = \sum_{n=1}^{N} \left( y_n - f( \mathbf{x}_n )\right)^2\\
\end{align*}
最小とする関数$f$のパラメータを求めます。つまり全てのデータに対して均等に誤差が小さくなるようにパラメータを求めます。
対して重み付き回帰では、以下のような目的関数になり
\begin{align*}
F = \sum_{n=1}^{N} g _n \left( y_n - f( \mathbf{x}_n) \right)^2\\
\end{align*}
各データに対して解析者が重み$g _n$を与えることで、どのデータについて誤差を小さくしたいかを各データごとに任意で決めることができます。つまり重み付き回帰では重み付きの誤差が小さくなるように関数$f$のパラメータを求めます。もちろん全ての重みが一定$g _n = {\rm constant}$のとき通常の回帰と一致します。
このような各データに対して重みをつけたいという状況はままあります。
例えば各都市にある工場の数から空気中の化学物質暴露量を予想したい状況を考えてみましょう。
空気中の化学物質暴露量の測定には技術が必要で、玄人計測士はかなりよい精度で測定することができますが、忙しく何箇所も測定することが難しいとしましょう。逆に見習い測定士は測定精度は低いですが、手が空いており多くの都市を測定できるとします(図11)。
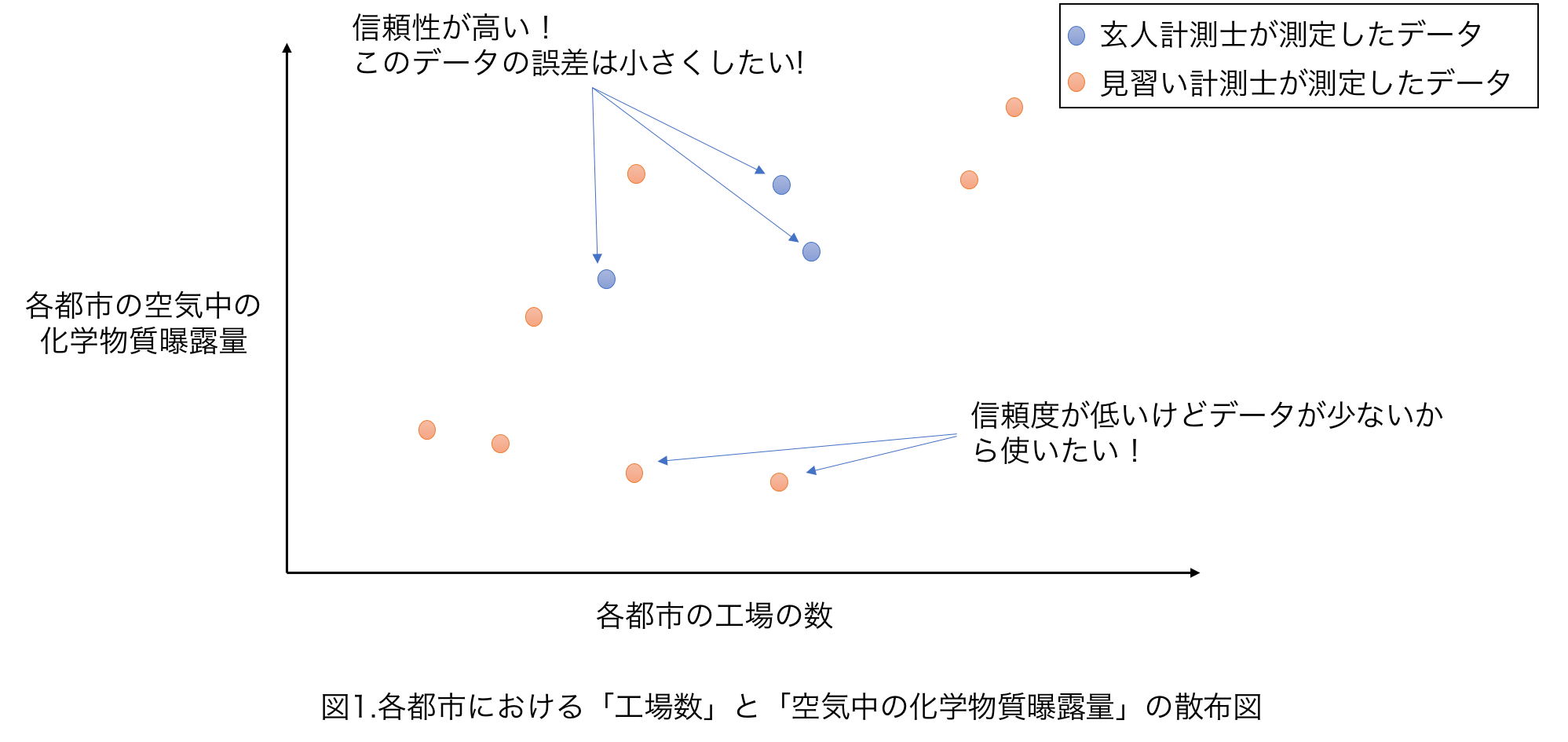
このような玄人計測士が測定したデータは信頼できるため、誤差をなるべく小さく(重み$g$を大きく)したいといった状況の時、重み付き回帰がなかなか使えます。
重み付き線形回帰の問題設定
それでは本題の双対表現を得るために、ちゃっちゃか式変形をしていきます。
重み付き線形回帰のタスクは$N$個の入力$\mathbf{x}_n \in \mathbb{R}^D$と出力$y_n \in \mathbb{R}$のペアと、各データに対する重み$G = {\rm diag}(g _1, \dots, g _N)$が与えられた時に、以下の目的関数を最小とするようなパラメータ$\mathbf{w}$を求めることになります。
\begin{align*}
F = \frac{1}{2} \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) + \frac{\beta}{2} \mathbf{w}^T \mathbf{w} \\
\tag{3}
\end{align*}
ここで$X$は入力$\mathbf{x} _n$を並べた行列$X = (\mathbf{x}_1, \dots, \mathbf{x} _N)\in \mathbb{R} ^{D \times N}$で、$\mathbf{y}$は出力$y _n$を並べたベクトル$(y _1, \dots, y _N) \in \mathbb{R} ^N$です。
解いてみた
最小二乗法でおなじみの式(3)を$\mathbf{w}$で偏微分して$0$とおくことで、最適なパラメータを求めましょう。
\begin{align*}
\frac{\partial F}{\partial \mathbf{w}} &= \frac{\partial }{\partial \mathbf{w}} \left\{ \frac{1}{2} \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) + \frac{\beta}{2} \mathbf{w}^T \mathbf{w} \right\} \\
&= \frac{\partial }{\partial \mathbf{w}} \left\{ \frac{1}{2} \left( \mathbf{y}^T G \mathbf{y} - 2 \mathbf{w}^T X^T G \mathbf{y} + \mathbf{w}^T X^T G X\mathbf{w} \right) + \frac{\beta}{2} \mathbf{w}^T \mathbf{w} \right\} \\
&= - X^T G \mathbf{y} + X^T G X \mathbf{w} + \beta \mathbf{w} \\
&= - X^T G \mathbf{y} + \left( X^T G X + \beta I \right) \mathbf{w} \\
&= 0
\end{align*}
より
\begin{align*}
\left( X^T G X + \beta I \right) \hat{\mathbf{w}} = X^T G \mathbf{y} \\
\hat{\mathbf{w}} = \left( X^T G X + \beta I \right)^{-1} X^T G \mathbf{y}
\tag{4}
\end{align*}
となり、パラメータが推定できました!
次はメインディッシュの双対表現を求めていきましょう!
通常は$\mathbf{w} = \alpha X$とおいて、$\alpha$について解いていき双対表現を求めていきますが、
今回は逆行列の補助定理(Sherman–Morrison–Woodburyの公式)1を使って求めていきます。
まず、$H \triangleq \beta I$とおき式(4)を
\begin{align*}
\hat{\mathbf{w}} &= \left( X^T G X + H \right)^{-1} X^T G \mathbf{y} \\
&= \left( H + X^T G X \right)^{-1} X^T G \mathbf{y}
\tag{5}
\end{align*}
と書きなおします。
ここでpush through identity(証明)
\begin{align*}
\left( A + BCD \right)^{-1} B = A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} C^{-1} \\
\end{align*}
を使って式変形をしていきます。$A = H、B = X^T,C = G, D = X$とみなすと式(5)は
\begin{align*}
\hat{\mathbf{w}} &= \left( H + X^T G X \right)^{-1} X^T G \mathbf{y} \\
&= H^{-1}X^T \left( XH^{-1}X^T + G^{-1} \right)^{-1} G^{-1} G \mathbf{y} \\
&= H^{-1}X^T \left( XH^{-1}X^T + G^{-1} \right)^{-1} \mathbf{y}
\tag{6}
\end{align*}
となり、双対表現が得られました!!
ちなみに式(6)の結果を使って新規入力に対する出力の予測値$\hat{\mathbf{y}}$を求めて見ると
\begin{align*}
\hat{\mathbf{y}} &= X \hat{\mathbf{w}} \\
&= X H^{-1}X^T \left( XH^{-1}X^T + G^{-1} \right)^{-1} \mathbf{y} \\
\end{align*}
となります。またここで$K \triangleq X H^{-1}X^T$とおくと
\begin{align*}
\hat{\mathbf{y}} = K \left( K + G^{-1} \right)^{-1} \mathbf{y} \\
\end{align*}
となり、みなさんがよく目にする式になります。
実装編
いま、信頼性が高いデータが10点(赤点)と信頼性が低いデータが30点(青点)与えられた時の回帰をやってみましょう。
データは以下のようになります。横軸が入力で縦軸が出力です。
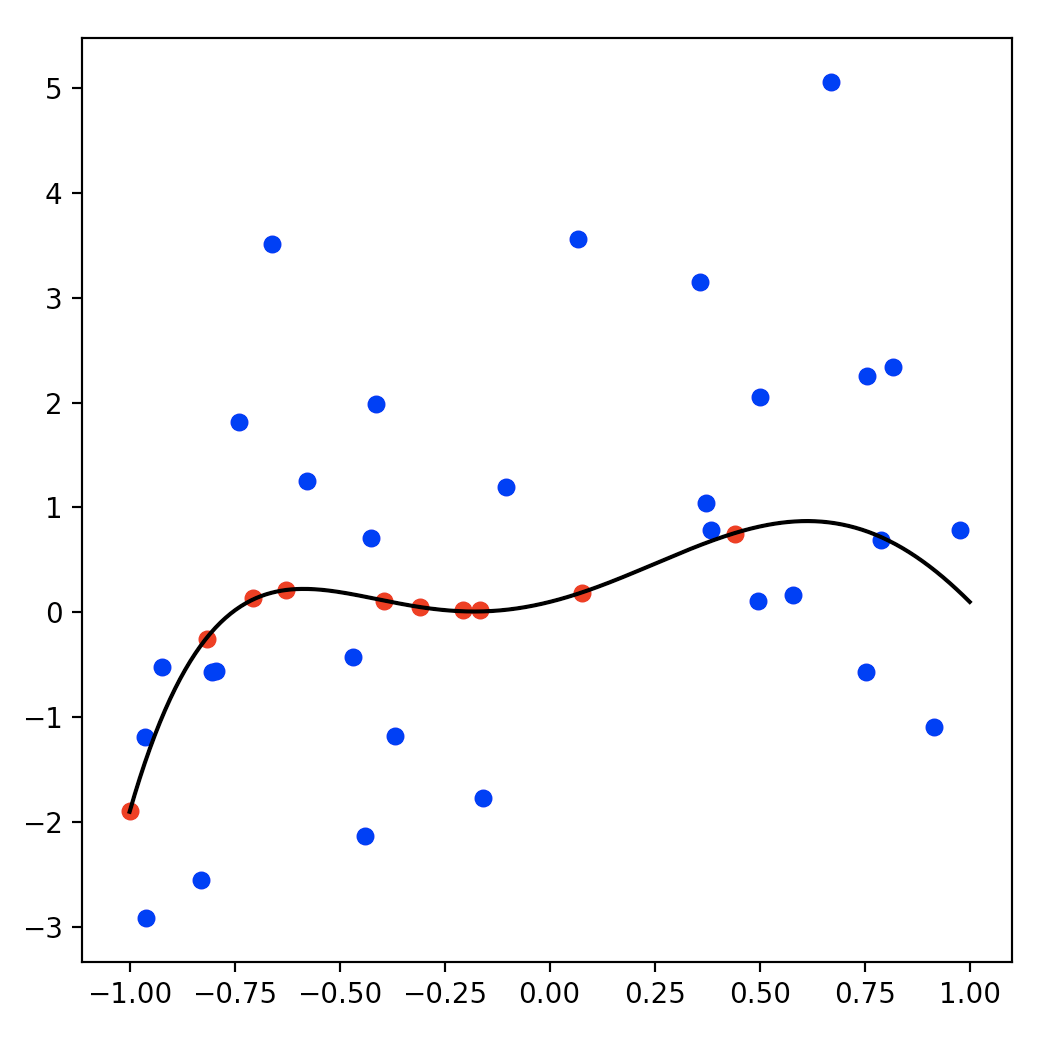
黒線が真の関数を表してます。
このデータに対して、重み付き回帰を行ってみましょう!
コードは以下のようになります。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
# ---------- データ生成 ---------- #
M = 5
w = np.array([0.1, 1.0, 2.5, -2.0, -3.5, 2.0]) # 真の関数のパラメータ
power = np.arange(M+1)
# 信頼性が高いデータ(ノイズの分散0.01)
N1 = 10
x1 = (np.random.rand(N1) * 2 - 1)[:, np.newaxis]
y1 = x1**power @ w + np.random.normal(0, 0.01, N1)
# 信頼性が低いデータ(ノイズの分散2.0)
N2 = 30
x2 = (np.random.rand(N2) * 2 - 1)[:, np.newaxis]
y2 = x2**power @ w + np.random.normal(0, 2.0, N2)
# 連結
N = N1 + N2
x = np.concatenate([x1, x2])
y = np.concatenate([y1, y2])
# 真の関数
x_all = (np.linspace(-1, 1, 500))[:, np.newaxis]
true_y = x_all**power @ w
# ---------- データの重みと正則化項 ---------- #
g1 = np.ones(N1) * 100.0 # 重みはノイズの分散の逆数が良き
g2 = np.ones(N2) * 0.5
beta = 0.1
G = np.diag(np.concatenate([g1, g2]))
H = np.eye(M+1) * beta
# ---------- パラメータ推定 ---------- #
# 基底関数の準備(M次多項式)
Phi = x**power
# 通常のリッジ回帰
w = np.linalg.pinv(Phi.T @ Phi + H) @ Phi.T @ y
f = x_all**power @ w
# 重み付き回帰
w_weight_regression = np.linalg.pinv(Phi.T @ G @ Phi + H) @ Phi.T @ G @ y
f_weight_regression = x_all**power @ w_weight_regression
# 信頼度の高いデータだけ使った場合
Phi_x1_only = x1**power
w_x1_only = np.linalg.pinv(Phi_x1_only.T @ Phi_x1_only + H) @ Phi_x1_only.T @ y1
f_x1_only = x_all**power @ w_x1_only
# ---------- 描画 ---------- #
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
ax.scatter(x1, y1, s=30, c='red')
ax.scatter(x2, y2, s=30, c='blue')
ax.plot(x_all, true_y, c='black') # 真の関数
ax.plot(x_all, f, c='green') # 普通のリッジ回帰
ax.plot(x_all, f_weight_regression, c='yellow') # 重み付き回帰
ax.plot(x_all, f_x1_only, c='pink') # 信頼性の高いデータだけ使ったリッジ回帰
plt.show()
結果がこちらになります。黄色の曲線が重み付き回帰で求めたパラメータを使った関数です。
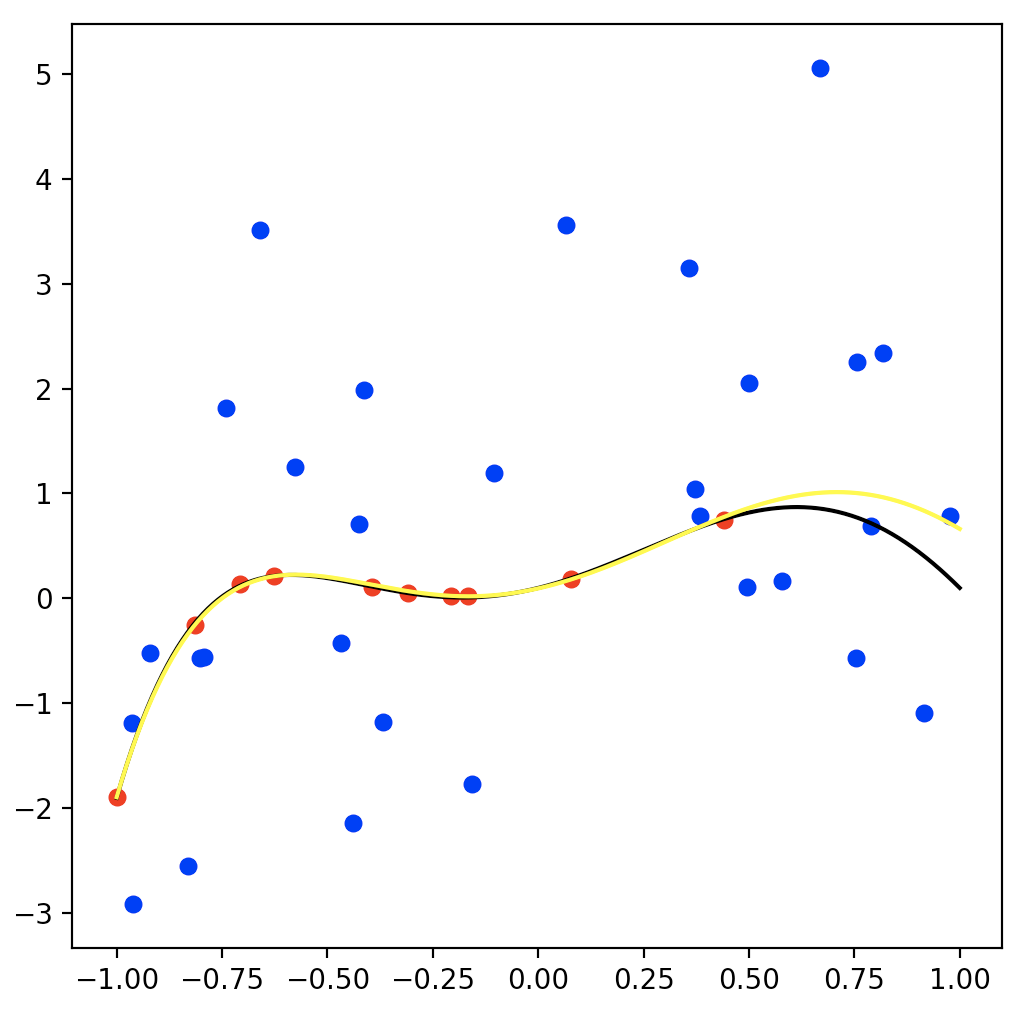
まぁまぁ真の関数を表現できてますね。やった。
ちなみに比較対象として、「普通のリッジ回帰(緑)」と「信頼性の高いデータだけ使ったリッジ回帰(ピンク)」を一緒に実行した結果がこちらです。
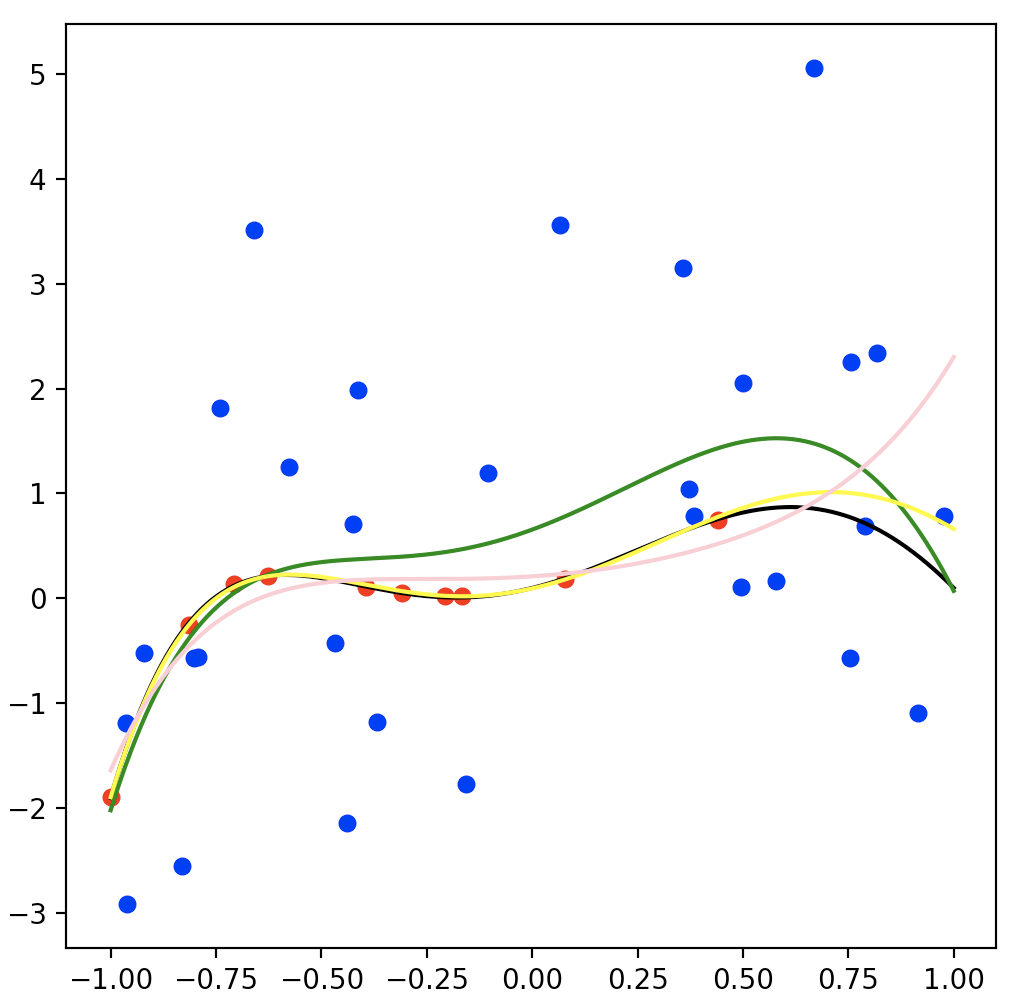
普通のリッジ回帰の結果(緑)は信頼性の低いデータ(青点)に引っ張られている感じで、重み付き回帰より真の関数がうまく推定できてないですね。
信頼性の高いデータだけ使ったリッジ回帰の結果(ピンク)はデータ点があるところは真の関数と近いですが、右の方のデータ点が存在しないところは少し真の関数からずれてますね。
こんな感じで、データの信頼度(ノイズの大きさ)がわかっている場合では重み付き回帰が効果的なのがわかりますね。
おまけ1:GとHの解釈について
結論から言うと実は$G = {\rm diag}(g _1, \dots, g _N)$の$g _n$は$n$番目のデータに乗っているガウスノイズの精度パラメータと解釈することができます。また$H = \beta I$の$\beta$は関数パラメータ$\mathbf w$の事前分布(ガウス分布)の精度パラメータと解釈できます。
つまり、$G$はデータのノイズの大きさを表現しており$H$は**関数(パラメータ)**の取りうる範囲を表現しているといった風になります。
なぜこのように解釈できるかはベイズ回帰(MAP推定)を考えてみるとわかりやすいので、簡単にですがみていきましょう。
まず、観測データ$\left( \mathbf{x} _n, y _n \right) _{n=1}^{N}$に対して以下のような確率モデルを考えます。
\begin{align*}
& y_n = \mathbf{w}^T \mathbf{x}_n + \epsilon_n \\
& \epsilon \sim N(0, \alpha^{-1}) \tag{7}\\
& \mathbf{w} \sim N(0, \beta^{-1}I) \tag{8}\\
\end{align*}
ここで推定したいパラメータ$\mathbf{w}$の対数事後分布はベイズの公式より
\begin{align*}
\ln p(\mathbf{w}|\mathbf{y}, X) &= \ln \frac{p(\mathbf{y}|\mathbf{w}, X)p(\mathbf{w})}{p(\mathbf{y}|X)} \\
&= \ln p(\mathbf{y}|\mathbf{w}, X) + \ln p(\mathbf{w}) - \ln p(\mathbf{y}|X)
\tag{9}
\end{align*}
となります。また
\begin{align*}
& p(\mathbf{y}|\mathbf{w}, X) = \prod _n p(\mathbf{y}_n|\mathbf{w}, \mathbf{x}_n) = \prod _n N(\mathbf{w}^T \mathbf{x}_n, \alpha^{-1}) \\
& p(\mathbf{w}) = N(0, \beta^{-1}I)
\end{align*}
であるから、式(9)は
\begin{align*}
\ln p(\mathbf{w}|\mathbf{y}, X) &= \ln N(\mathbf{w}^T \mathbf{x}_n, \alpha^{-1}) + \ln N(0, \beta^{-1}I) - \ln p(\mathbf{y}|X) \\
&= -\frac{\alpha}{2} \| \mathbf{y} - X \mathbf{w} \|^2 - \frac{\beta}{2}\| \mathbf{w} \| + C
\end{align*}
となります。2ただし$C$は$\mathbf{w}$について定数となるものをまとめた係数です。
さらに$G = \alpha I$とおき$H = \beta I$とおくと、
\begin{align*}
\ln p(\mathbf{w}|\mathbf{y}, X) = - \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) - \mathbf{w}^T H \mathbf{w} + C
\end{align*}
といった、重み付き線形回帰の目的関数とよく似たものがでてきます。
$G=\alpha I$は式(7)からわかるようにノイズの精度パラメータであり、$H=\beta I$は式(8)からわかるようにパラメータ$\mathbf{w}$に関する事前分布のパラメータです。
おまけ2:定理とかの証明
push through identityの証明
まず$B + BCDA^{-1}B$っていう天から落ちて来た式を左から$BC$でくくると
\begin{align*}
B + BCDA^{-1}B = BC \left( C^{-1} + DA^{-1}B \right)
\end{align*}
となります。また同じものを右から$A^{-1}B$でくくると
\begin{align*}
B + BCDA^{-1}B = \left( A + BCD \right) A^{-1}B
\end{align*}
となり、
\begin{align*}
BC \left( C^{-1} + DA^{-1}B \right) = \left( A + BCD \right) A^{-1}B
\end{align*}
という等式が得られます。そして両辺に対して右から$\left( C^{-1} + DA^{-1}B \right)^{-1}$と左から$\left( A + BCD \right)^{-1}$をそれぞれ掛けると
\begin{align*}
\left( A + BCD \right)^{-1} BC \left( C^{-1} + DA^{-1}B \right) \left( C^{-1} + DA^{-1}B \right)^{-1} &= \left( A + BCD \right)^{-1} \left( A + BCD \right) A^{-1}B \left( C^{-1} + DA^{-1}B \right)^{-1}\\
\left( A + BCD \right)^{-1} BC &= A^{-1}B \left( C^{-1} + DA^{-1}B \right)^{-1}
\end{align*}
となります。
さらにこれに右から$C^{-1}$を掛けてあげると
\begin{align*}
\left( A + BCD \right)^{-1} B = A^{-1}B \left( C^{-1} + DA^{-1}B \right)^{-1} C^{-1}
\end{align*}
となって、証明終了
ちなみにpush through identityは逆行列の補助定理(証明)
\begin{align*}
\left( A + BCD \right)^{-1} = A^{-1} - A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \\
\end{align*}
と、push through rule(証明)
\begin{align*}
A \left( I + BA \right)^{-1} = \left( I + AB \right)^{-1} A \\
\end{align*}
を組み合わせたもので、証明の手順はpush through ruleにならってます。
逆行列の補助定理の証明
実際に積をとって単位行列になるか確認します。
途中、ごちゃごちゃしてるようにみえるけど単に分配法則を適用してるだけです。
\begin{align*}
\left( A + BCD \right) \left[ A^{-1} - A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \right]
&= \left\{ I - B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1}\right\} \\
& + \left\{ BCDA^{-1} - BCD A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \right\} \\
&= \left\{ I + BCDA^{-1} \right\} \\
& - \left\{ B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} + BCD A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \right\} \\
&= I + BCDA^{-1} - \left( B + BCD A^{-1}B \right) \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \\
&= I + BCDA^{-1} - BC \left(C^{-1} + D A^{-1}B \right) \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \\
&= I + BCDA^{-1} - BCDA^{-1} \\
&= I \\
\end{align*}
証明終了
push through ruleの証明
まず、$A + ABA$を$A$でくくると
\begin{align*}
A + ABA = A \left( I + BA \right) \\
A + ABA = \left( I + AB \right) A \\
\end{align*}
となるので、
\begin{align*}
A \left( I + BA \right) = \left( I + AB \right) A \\
\end{align*}
の等式が得られます。次にそれらに右から$\left( I + AB \right)^{-1}$を掛けると
\begin{align*}
A = \left( I + AB \right) A \left( I + BA \right)^{-1} \\
\end{align*}
となり、さらに両辺に左から$\left( I + BA \right)^{-1}$を掛けると
\begin{align*}
\left( I + BA \right)^{-1} A = A \left( I + BA \right)^{-1} \\
\end{align*}
となって証明終了
おまけ3:基底関数のバージョン
目的関数
\begin{align*}
F = \frac{1}{2} \left( \mathbf{y} - \Phi \theta \right)^T G \left( \mathbf{y} - \Phi \theta \right) + \frac{1}{2} \theta^T H \theta\\
\end{align*}
$\mathbf{y} \in \mathbb{R} ^N$:出力($N$個のデータ)
$\Phi \in \mathbb{R} ^{N \times M}$:計画行列($M$個の基底関数)
$\theta \in \mathbb{R} ^M$:パラメータ
$G \in \mathbb{R} ^{N \times N}$:データの重み(対称行列)
$H \in \mathbb{R} ^{M \times M}$:正則化項の重み(対称行列)
推定したパラメータ
・基底関数表現
\begin{align*}
\hat{\theta} = \left( \Phi^T G \Phi + H\right)^{-1}\Phi^T G \mathbf{y} \\
\end{align*}
・カーネル表現
\begin{align*}
\hat{\theta} = H^{-1} \Phi^T \left( \Phi H^{-1} \Phi^T + G^{-1} \right)^{-1} \mathbf{y} \\
\end{align*}