この記事は古川研究室 Workout_calendar 10日目の記事です。
$\newcommand{\argmax}{\mathop{\rm arg~max}\limits}$
今回は正準相関分析（Canonical Correlation Analysis: CCA）の解説をしていきます。
CCAはだーいぶ古い手法で「なぜ？今更解説？」ってなるかもしれないけど、計算途中まで書いてある日本語の記事が何気に少なかったらから書いてみようかなと思った次第です。
あと最近マルチドメインとかよく聞くから、これを機にCCAの知名度をあげていきたいなーと思ってます。PCAぐらいメジャーにさせてあげたいです。

はじめに

CCAは転移学習やデータ融合や情報推薦などの様々な分野で耳にするマルチビューデータ（マルチモーダルとかマルチドメインとかクロスドメインとか色んな呼ばれ方してるやつ）に対する古典的な解析手法の１つです。
個人的にCCAはマルチビューデータ界の主成分分析(PCA)だと思ってます。ですのでマルチビューデータを扱う研究をしてるけど、CCAは知らないって方は是非、目を通してみてください！

忙しい人のためのCCA

CCAとは
　CCAはマルチビューデータの解析手法。共通成分を抽出して色んなことができる。

CCAのタスク
　Input：データ$X = (\mathbf x_n) \in \mathbb{R}^{D_x \times N}, Y = \mathbf (y_n) \in \mathbb{R}^{D_y \times N}$
　　　　$N$：データ数、$D_x, D_y$：データの次元数、$\frac{1}{N}\Sigma_n \mathbf x_n = \frac{1}{N}\Sigma_n \mathbf y_n = 0$
　Task：

\begin{align*}
 \mathbf a,  \mathbf b = \argmax_{\mathbf a, \mathbf b}\mathbf a^T S_{xy} \mathbf b \quad　s.t.　\mathbf a^T S_{xx} \mathbf a = \mathbf b^T S_{yy} \mathbf b = 1
\end{align*}

　ここで、$S_{xx} = \frac{1}{N}XX^T, S_{yy} = \frac{1}{N}YY^T, S_{xy} = \frac{1}{N}XY^T$です。

解
　行列$S_a, S_b$の最大の固有値に対応する固有ベクトルが求めるべき線形変換$\mathbf a, \mathbf b$になります。

\begin{align*}
S_a \mathbf a &= \lambda_a \mathbf a \\ 
S_b \mathbf b &= \lambda_b \mathbf b
\end{align*}

\begin{align*}
\mbox{where} \quad S_a = S^{-1}_{xx}S_{xy}S^{-1}_{yy}S_{yx},S_b = S^{-1}_{yy}S_{yx}S^{-1}_{xx}S_{xy}
\end{align*}

　もしくは、行列$S_{xx}^{-1/2}S_{xy}S_{yy}^{-1/2}$の最大の特異値に対応する左特異ベクトルを$\mathbf u$、右特異ベクトルを$\mathbf v$としたとき、求めるべき線形変換$\mathbf a , \mathbf b$は

\begin{align*}
\mathbf a = S^{-\frac{1}{2}}_{xx} \mathbf u \\
\mathbf b = S^{-\frac{1}{2}}_{yy} \mathbf v \\
\end{align*}

　となります¹。

正準相関分析とは？

一言で言うと、CCAは「色んなセンサーで計測したデータ（マルチビューデータ）から共通成分²を抽出する解析手法」です。
CCAを含め多くのマルチビュー解析手法はデータ間に共通する情報を抽出することを目的にしています。ただし「共通」の「定義」もしくは「基準」が解析手法ごとに異なり、この定義の違いがそのまま各手法の特色になります。
CCAでは「相関係数が高い＝共通している³」を信念に、各ビューデータを線形変換した値（共通成分）の間の相関係数が大きくなるように線形変換を求めています。

共通成分をGetして何が嬉しいの？

各ビューデータ間に共通する成分を抽出するモチベーションは、大きく分けると以下の3つになります。

良い特徴を選択したい！⁴（共通成分の抽出そのものがモチベーション）
ノイズの除去をしたい！⁵
片方のビューデータから他方のビューデータを予測したい！⁶

問題設定

今回は2種類の観測方法によって得られたデータ(2ビューデータ)が与えられた場合を説明します。ちなみに3ビュー以上の場合は一般化正準相関分析という枠組みになり、少しだけ難しくなります。
それでは本題に移ります。

まずはデータについて色々と定義していきます。
今、$N$個の対象に対して２つの観測方法によって得られたデータを${(\mathbf x_n, \mathbf y_n)}^N_{n=1}$とします。
ただし$\mathbf x \in \mathbb{R}^{D_x}$、$\mathbf y \in \mathbb{R}^{D_y}$とします。計算を簡単にするため各ビューのデータの平均$E[\mathbf x], E[\mathbf y]$は$\mathbf ０$とします。また$E[f(x)]$はアンサンブル平均

\begin{align*}
E[f(x)]=\frac{1}{N}\sum^{N}_{n=1} f(x_n)
\end{align*}

を表します。
次にデータを線形変換して得られる共通成分$u_x, v_n$を考えます。

\begin{align*}
u_n &= \mathbf a^T \mathbf x_n \\
v_n &= \mathbf b^T \mathbf y_n
\end{align*}

この時、CCAのタスクは共通成分$u, v$の間の相関係数$\rho(\mathbf a, \mathbf b)$が最大となるような線形変換$\mathbf a, \mathbf b$を求めることです。

\begin{align*}
\mathbf a, \mathbf b = \argmax_{\mathbf a, \mathbf b}\rho (\mathbf a, \mathbf b) \tag{1}
\end{align*}

ちなみに相関係数は

\begin{align*}
\rho (\mathbf a, \mathbf b) &= \frac{E[uv]}{\sqrt{E[u^2]}\sqrt{E[v^2]}} \\
&= \frac{E[(\mathbf a^T \mathbf x)(\mathbf b^T \mathbf y)]}{\sqrt{E[(\mathbf a^T \mathbf x)(\mathbf a^T \mathbf x)]}\sqrt{E[(\mathbf b^T \mathbf y)(\mathbf b^T \mathbf y)]}} \\
&= \frac{E[\mathbf a^T \mathbf x \mathbf y^T \mathbf b]}{\sqrt{E[\mathbf a^T \mathbf x\mathbf x^T \mathbf a]}\sqrt{E[\mathbf b^T \mathbf y \mathbf y^T \mathbf b]}} \\
&= \frac{\mathbf a^T E[\mathbf x \mathbf y^T] \mathbf b}{\sqrt{\mathbf a^T E[\mathbf x\mathbf x^T] \mathbf a}\sqrt{\mathbf b^T E[\mathbf y \mathbf y^T] \mathbf b}} \end{align*}

ここで、$S_{xx} = E[\mathbf x\mathbf x^T],S_{yy} = E[\mathbf y\mathbf y^T],S_{xy} = E[\mathbf x\mathbf y^T]$とおくと

\begin{align*}
= \frac{\mathbf a^T S_{xy} \mathbf b}{\sqrt{\mathbf a^T S_{xx} \mathbf a}\sqrt{\mathbf b^T S_{yy} \mathbf b}} \tag{2}
\end{align*}

となります。ここで式（2）をよくみてみると、$\mathbf a, \mathbf b$に0以上のスカラーをかけても分子分母で相殺され、$\rho (\mathbf a, \mathbf b)$の値が変わらないことが分かります。つまり$\mathbf a, \mathbf b$に何かしらの正の数を掛けて、$\mathbf a^T S_{xx} \mathbf a = \mathbf b^T S_{yy} \mathbf b = 1$としてもCCAの問題を解く際になんら影響ないと言えます。
したがってCCAのタスクは式（１）から

\begin{align*}
\argmax_{\mathbf a, \mathbf b} \mathbf a^T S_{xy} \mathbf b \quad　s.t.　\mathbf a^T S_{xx} \mathbf a = \mathbf b^T S_{yy} \mathbf b = 1 \tag{3}
\end{align*}

となります。

実際に解いてみる

それでは、次にCCAのタスクを実際に解いて線形変換$\mathbf a, \mathbf b$を求めていきます。式変形が長いので、流れを先に伝えます。

　1. 式(3)を変形し、一般化固有値問題に帰着させる
　2. 式変形を行い一般化固有値問題を通常の固有値問題にする
　3. おまけ:コーシー＝シュワルツの不等式とかを用いて線形変換$\mathbf a, \mathbf b$を算出する

一般化固有値問題への帰着

まず式(3)のような制約付きの極値問題はラグランジュの未定乗数法を用いることで、

\begin{align*}
L(\mathbf a, \mathbf b, \lambda_a, \lambda_b) = \mathbf a^T S_{xy} \mathbf b + \lambda_a(1 - \mathbf a^T S_{xx} \mathbf a) + \lambda_b(1 - \mathbf b^T S_{yy} \mathbf b) \tag{4}
\end{align*}

という$\mathbf a, \mathbf b, \lambda_a, \lambda_b$についての単なる極値問題に置きかわります。単なる極値問題になったらその関数$L$を$\mathbf a$と$\mathbf b$で偏微分し、$\mathbf 0$とおくことで、簡単に最適なパラメータを求めることができます。
ではやってみましょう。

\begin{align*}
\frac{\partial L }{\partial \mathbf a} = S_{xy} \mathbf b - 2 \lambda_a S_{xx} \mathbf a = \mathbf 0 \\
\frac{\partial L }{\partial \mathbf b} = S^T_{xy} \mathbf a - 2 \lambda_b S_{yy} \mathbf b = \mathbf 0
\end{align*}

より

\begin{align*}
S_{xy} \mathbf b &= 2 \lambda_a S_{xx} \mathbf a \tag{5} \\
S^T_{xy} \mathbf a &=  2 \lambda_b S_{yy} \mathbf b \tag{6}
\end{align*}

また式(5)の左から$\mathbf a^T$をかけると、

\begin{align*}
\mathbf a^T S_{xy} \mathbf b &= 2 \lambda_a \mathbf a ^T S_{xx} \mathbf a \\
\mathbf a^T S_{xy} \mathbf b &=  2 \lambda_a
\end{align*}

となり、$\lambda_a$は相関係数そのものであることが分かります。また同様に式(6)の左からそれぞれ$\mathbf b^T$をかけると、

\begin{align*}
\mathbf b^T S^T_{xy} \mathbf a &=  2 \lambda_b \mathbf b^T S_{yy} \mathbf b \\
\mathbf b^T S^T_{xy} \mathbf a &=  2 \lambda_b \\
\mathbf a^T S_{xy} \mathbf b &=  2 \lambda_b
\end{align*}

となり、$\lambda_b$も相関係数そのものであることが分かります。
さらに$\lambda_a = \lambda_b$となるので、$\lambda \triangleq 2 \lambda_a$とおくと式(5)、式(6)は以下のようにまとめることができ、

\begin{align*}
\left(\begin{array}{cc}
O & S_{xy} \\
S^T_{xy} & O \\
\end{array}\right) \left(\begin{array}{c}
\mathbf a \\
\mathbf b \\
\end{array}\right) = \lambda \left(\begin{array}{cc}
S_{xx} & O \\
O & S_{yy} \\ 
\end{array}\right) \left(\begin{array}{c}
\mathbf a \\
\mathbf b \\
\end{array}\right) \tag{7}
\end{align*}

という一般化固有値問題となります。
ここで$\lambda_a, \lambda_b$が相関係数であったことを思い出すと、最も大きい固有値に対応する固有ベクトルが、相関係数を最大とする線形変換$\mathbf a, \mathbf b$となることが分かります。また線形変換で２次元以上に落としたい場合は、固有値が大きい順に対応する固有ベクトルをとればOKです⁷。ただし、${\rm min}(D_x, D_y)$より多くの次元はとることができません。
基本的に以上がCCAのアルゴリズムになります。だた今回はさらに式変形を行い、pythonとかでも簡単に実装できるよう通常の固有値問題に落とし込んでいきます。

一般化固有値問題から通常の固有値問題へ

まずは式(6)の左から逆行列$S^{-1}_{yy}$をかけることで、

\begin{align*}
S^{-1}_{yy} S^T_{xy} \mathbf a = \lambda \mathbf b \\
\mathbf b = \frac{S^{-1}_{yy} S^T_{xy} \mathbf a}{\lambda} \tag{8}
\end{align*}

という「$\mathbf b =$」の形に変形させます。つぎに式(8)を式(5)に代入して

\begin{align*}
S_{xy} \frac{S^{-1}_{yy} S^T_{xy} \mathbf a}{\lambda} &=  \lambda S_{xx} \mathbf a \\
S_{xy} S^{-1}_{yy} S^T_{xy} \mathbf a &= \lambda^2 S_{xx} \mathbf a \\
S_{xx}^{-1} S_{xy} S^{-1}_{yy} S^T_{xy} \mathbf a &= \lambda^2 \mathbf a \\
\end{align*}

って変形します。さらに$S^T_{xy} = S_{yx}$より、

\begin{align*}
S_{xx}^{-1} S_{xy} S^{-1}_{yy} S_{yx} \mathbf a = \lambda^2 \mathbf a \\
\end{align*}

となり通常の固有値問題になりました。つまり求めるべき線形変換$\mathbf a$は行列$S_{xx}^{-1} S_{xy} S_{yy}^{-1} S_{yx}$の固有ベクトルであるということです。
では、次に同様に線形変換$\mathbf b$についても固有値問題へと式変形していきます。
まずは式(5)の左から逆行列$S^{-1}_{xx}$をかけることで、

\begin{align*}
S^{-1}_{xx} S_{xy} \mathbf b = \lambda \mathbf a \\
\mathbf a = \frac{S^{-1}_{xx} S_{xy} \mathbf b}{\lambda} \tag{9}
\end{align*}

という「$\mathbf a =$」の形に変形させ、そして式(9)を式(6)に代入することで

\begin{align*}
S^T_{xy} \frac{S^{-1}_{xx} S_{xy} \mathbf b}{\lambda} &=  \lambda S_{yy} \mathbf b \\
S^T_{xy} S^{-1}_{xx} S_{xy} \mathbf b &= \lambda^2 S_{yy} \mathbf b \\
S_{yy}^{-1} S^T_{xy} S^{-1}_{xx} S_{xy} \mathbf b &= \lambda^2 \mathbf b \\
S_{yy}^{-1} S_{yx} S^{-1}_{xx} S_{xy} \mathbf b &= \lambda^2 \mathbf b \\
\end{align*}

といった感じで線形変換$\mathbf b$についても固有値問題になりました。
まとめると、線形変換$\mathbf a, \mathbf b$はそれぞれ以下の行列の固有値問題を解くことで、求めることができるということになります。

\begin{align*}
S_{xx}^{-1} S_{xy} S^{-1}_{yy} S_{yx} \mathbf a = \lambda^2 \mathbf a \tag{10}\\
S_{yy}^{-1} S_{yx} S^{-1}_{xx} S_{xy} \mathbf b = \lambda^2 \mathbf b \tag{11} \\
\end{align*}

おまけ：特異値分解をつかって線形変換の算出

固有値問題すら解きたくない！って人のために特異値分解で線形変換$\mathbf a, \mathbf b$を算出できる方法を説明します。だいたいこれとこれに載ってる内容と同じです。
それでは始めていきましょう。まず今回の出発点は相関係数の式からになります。

\begin{align*}
\rho (\mathbf a, \mathbf b)= \frac{\mathbf a^T S_{xy} \mathbf b}{\sqrt{\mathbf a^T S_{xx} \mathbf a}\sqrt{\mathbf b^T S_{yy} \mathbf b}}
\end{align*}

ここで以下のように基底変換を行います。

\begin{align*}
\mathbf c = S_{xx}^{\frac{1}{2}} \mathbf a \\
\mathbf d = S_{yy}^{\frac{1}{2}} \mathbf b \\
\end{align*}

すると、相関係数の式は

\begin{align*}
\rho (\mathbf c, \mathbf d) &= \frac{\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} \mathbf d}{\sqrt{\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xx} S_{xx}^{-\frac{1}{2}} \mathbf c}\sqrt{\mathbf d^T S_{yy}^{-\frac{1}{2}} S_{yy} S_{yy}^{-\frac{1}{2}} \mathbf d}} \\
&= \frac{\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} \mathbf d}{\sqrt{\mathbf c^T \mathbf c}\sqrt{\mathbf d^T \mathbf d}}
\end{align*}

となります。ここで、

\begin{align*}
\mathbf w &= S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \mathbf c \\
\mathbf z &= \mathbf d
\end{align*}

とおくとコーシー＝シュワルツの不等式より$\left| \left< \mathbf w, \mathbf z \right> \right|^2 \leq \left< \mathbf w, \mathbf w \right> \cdot \left< \mathbf z, \mathbf z \right>$という不等式ができます。よって

\begin{align*}
\left(\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}}\right) \left(\mathbf d \right) &\leq \left(\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \mathbf c \right)^{\frac{1}{2}} \left(\mathbf d^T \mathbf d \right)^{\frac{1}{2}} \tag{12}\\
\end{align*}

が成り立ち、これを式変形していくと

\begin{align*}
\frac{\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}}\mathbf d}{\left(\mathbf d^T \mathbf d \right)^{\frac{1}{2}}} &\leq \left(\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \mathbf c \right)^{\frac{1}{2}} \\
\frac{\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}}\mathbf d}{\left(\mathbf c^T \mathbf c \right)^{\frac{1}{2}}\left(\mathbf d^T \mathbf d \right)^{\frac{1}{2}}} &\leq \frac{\left(\mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \mathbf c \right)^{\frac{1}{2}}}{\left(\mathbf c^T \mathbf c \right)^{\frac{1}{2}}} \\
\end{align*}

になり、相関係数について

\begin{align*}
\rho \leq \frac{\left( \mathbf c^T S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \mathbf c\right)^{\frac{1}{2}}}{\left(\mathbf c^T \mathbf c\right)^{\frac{1}{2}}}\tag{13}
\end{align*}

という上限がとれます。また等号が成り立つのは

\begin{align*}
\mathbf d \propto S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \mathbf c
\end{align*}

のときです。式（12）に代入してみると明らかですね。
ここで一旦、この比例関係は置いておいて、

\begin{align*}
M \triangleq S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}}
\end{align*}

とおきます。すると式(13)は$\mathbf c$に対するレイリー商$R(M, \mathbf c) = \frac{\mathbf c^T M \mathbf c}{\mathbf c^T \mathbf c}$になっていることに気づきます！そして勿論、レイリー商の最大値は行列$M$の最大の固有値と等しく、このときの$\mathbf c$はその固有値に対応する固有ベクトルになっているので、相関係数を最大にする線形変換$\mathbf c$は、この固有ベクトルそのものになります。計算は省きますが$\mathbf b$にも同じようなことが言えます。
おそらくややこしくなってきたと思うので、ここまでの事実を一旦まとめます。
式(12)の等号が成り立ち、相関係数が最大かつになるとき

\begin{align*}
\mathbf d \propto S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \mathbf c
\end{align*}

が成り立ち、線形変換$\mathbf c$は行列

\begin{align*}
S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}} \tag{14}
\end{align*}

の最も大きい固有値に対応する固有ベクトルとイコールになります。
また線形変換$\mathbf d$についても、相関係数を最大にする$\mathbf d$は行列

\begin{align*}
S_{yy}^{-\frac{1}{2}} S_{xy} S_{xx}^{-\frac{1}{2}} S_{xx}^{-\frac{1}{2}} S_{yx} S_{yy}^{-\frac{1}{2}} \tag{15}
\end{align*}

の最も大きい固有値に対応する固有ベクトルになります。
ここで、

\begin{align*}
E \triangleq S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}}
\end{align*}

とすると式(14)、式(15)は

\begin{align*}
S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}} S_{yy}^{-\frac{1}{2}} S_{yx} S_{xx}^{-\frac{1}{2}}  = EE^T \\
S_{yy}^{-\frac{1}{2}} S_{xy} S_{xx}^{-\frac{1}{2}} S_{xx}^{-\frac{1}{2}} S_{yx} S_{yy}^{-\frac{1}{2}} = E^TE
\end{align*}

となり、$E$を特異値分解$E = U \Sigma V^T$すると、

\begin{align*}
EE^T = (U \Sigma V^T)(U \Sigma V^T)^T = U \Sigma^2 U^T \\
E^TE = (U \Sigma V^T)^T(U \Sigma V^T) = V \Sigma^2 V^T
\end{align*}

となります。
つまり、線形変換$\mathbf c, \mathbf d$はそれぞれ行列

\begin{align*}
S_{xx}^{-\frac{1}{2}} S_{xy} S_{yy}^{-\frac{1}{2}}
\end{align*}

の左特異ベクトル$\mathbf u$と右特異ベクトル$\mathbf v$になっているということになります。
よって、線形変換$\mathbf a, \mathbf b$は

\begin{align*}
\mathbf a = S^{-\frac{1}{2}}_{xx} \mathbf c = S^{-\frac{1}{2}}_{xx} \mathbf u\\
\mathbf b = S^{-\frac{1}{2}}_{yy} \mathbf d = S^{-\frac{1}{2}}_{yy} \mathbf v\\
\end{align*}

となります。終了です！お疲れ様でした！

実装

実装を簡単にするために、通常の固有値問題に落とし込んだり色々頑張ったけど、実際はスクラッチするよりsklearnのCCAパッケージが便利なので、CCAで何か解析したいときは素直にこちらを使いましょう。
今回は500の人を対象に問診(View 1)と精密検査(View 2)を実施し、データを収集したていで、診断結果という名の人工データをCCAで解析しましょう。今回は精密検査は時間もかかるし、コストも高いから簡単に調べられる問診から健康状態をCCAを使って予測しようってシナリオをデモンストレーションします。
得られたデータはこんな感じです(図1)。
点の色はその人の健康状態を表し、赤から青に変わるほどよいものとします。

　　　　　　　　　　　　　　　　　　　図1. 観測データ
　　　　　　　　　　左図：問診データでスコアが高ければ健康とは限らない
　　　　　　　　　　右図：精密検査データでスコアが高いほど健康である
　
実際は得られませんが、全くノイズが乗らなかった場合はこんな感じです。
共通成分（健康状態）の違いだけが観測データの変化に影響を与えている状況です

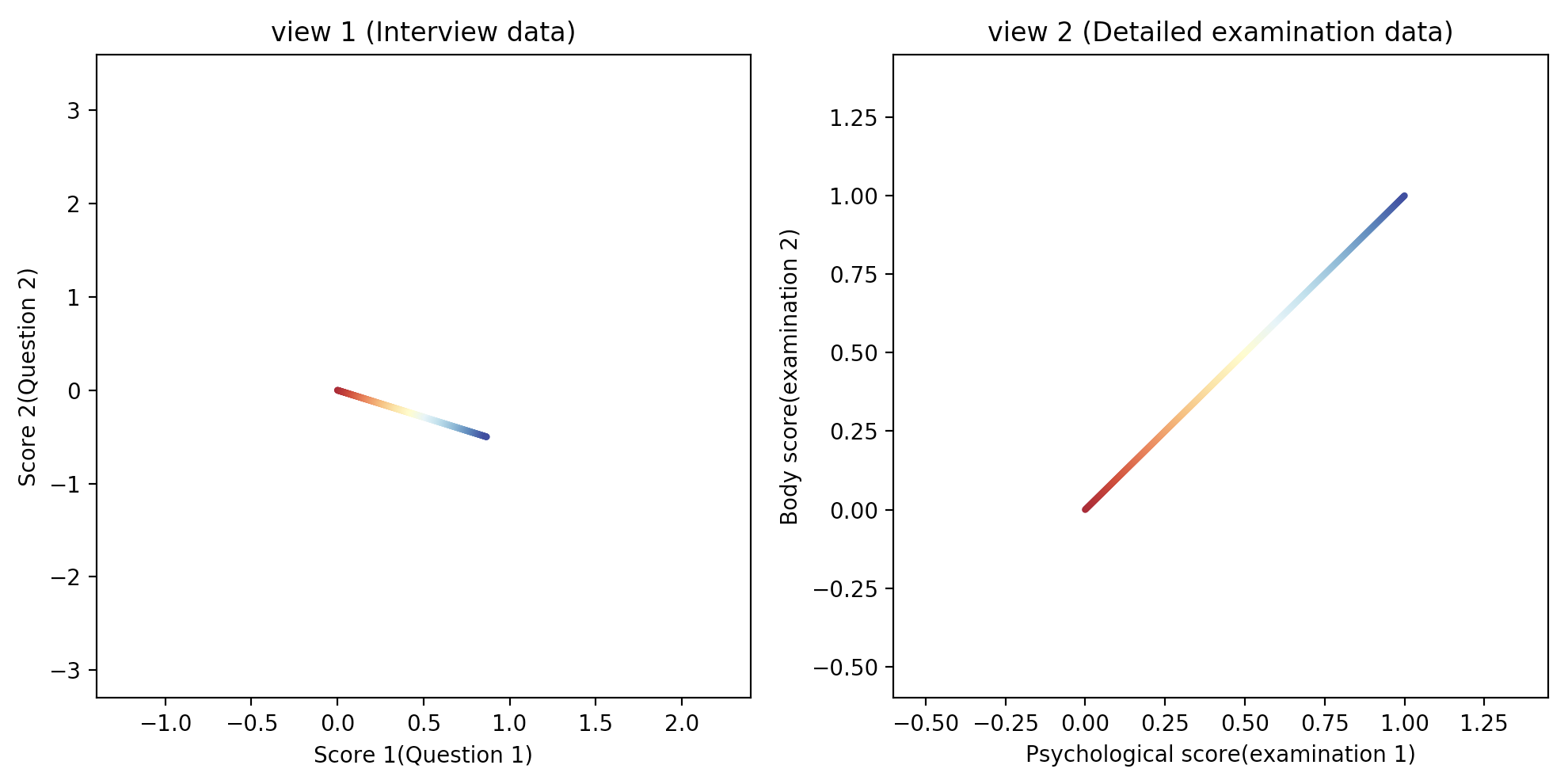
　　　　　　　　　　　　　　　　図2. ノイズなし観測データ

じゃあ早速CCAで解析しましょう。コードはこんな感じです。

from sklearn.cross_decomposition import CCA
import numpy as np
import math
import matplotlib.pyplot as plt

np.random.seed(1)

# ---------- データ準備 ---------- #
# 対象人数
N = 500

# 共通成分(健康状態0~1)
z = np.linspace(0, 1, N)
# 未学習のデータ生成用共通成分
z_non = 0.32424

# 回転角度
THETA = math.radians(30)
ROT = np.array([[np.cos(THETA), -np.sin(THETA)], [np.sin(THETA), np.cos(THETA)]])

# View 1:問診データ（質問内容は２つ）
D_x = 2
X = np.zeros((N, D_x))
X[:, 0] = z + np.random.normal(0, 0.2, size=(N,))
X[:, 1] = np.random.normal(0, 1, size=(N,))
X = X @ ROT

# View2:精密検査データ（検査内容は２つ）
D_y = 2
Y = np.zeros((N, D_y))
Y[:, 0] = z + np.random.normal(0, 0.2, size=(N,))
Y[:, 1] = z + np.random.normal(0, 0.2, size=(N,))

# ---------- 学習 ---------- #
# モデル構築
cca = CCA(n_components=1)
# 学習
cca.fit(X, Y)
# ノイズ除去
X_cca = X @ cca.x_weights_ @ cca.x_weights_.T
Y_cca = Y @ cca.y_weights_ @ cca.y_weights_.T

# 問診データから精密検査の結果を予想
# 未学習のデータ作成
X_non = np.zeros((1, D_x))
X_non[0, 0] = z_non + np.random.normal(0, 0.2, size=(1,))
X_non[0, 1] = np.random.normal(0, 1, size=(1,))
X_non = X_non @ ROT
Y_non = np.zeros((1, D_y))
Y_non[0, 0] = z_non + np.random.normal(0, 0.2, size=(1,))
Y_non[0, 1] = z_non + np.random.normal(0, 0.2, size=(1,))
# 予測
Y_predict = X_non @ cca.x_weights_ @ cca.y_weights_.T

# ---------- 描画 ----------#
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
N_color = np.linspace(0, 1.0, N)

ax1.scatter(X[:, 0], X[:, 1], c=N_color, cmap='RdYlBu', s=4)
ax2.scatter(Y[:, 0], Y[:, 1], c=N_color, cmap='RdYlBu', s=4)
ax1.scatter(X_cca[:, 0], X_cca[:, 1], c='black', s=4)
ax2.scatter(Y_cca[:, 0], Y_cca[:, 1], c='black', s=4)

ax1.scatter(X_non[0, 0], X_non[0, 1], c='red', s=300, marker='*')
# 本当の値
ax2.scatter(Y_non[0, 0], Y_non[0, 1], c='red', s=300, marker='*')
# 予測した値
ax2.scatter(Y_predict[0, 0], Y_predict[0, 1], c='blue', s=300, marker='*')

ax1.set_title('view 1 (Interview data)')
ax1.set_xlabel('Score 1(Question 1)')
ax1.set_ylabel('Score 2(Question 2)')

ax2.set_title('view 2 (Detailed examination data)')
ax2.set_xlabel('Psychological score(examination 1)')
ax2.set_ylabel('Body score(examination 2)')

ax1.set_xlim(-1.4, 2.4)
ax1.set_ylim(-3.3, 3.7)

ax2.set_xlim(-0.6, 1.45)
ax2.set_ylim(-0.6, 1.45)

plt.tight_layout()
plt.show()

　　　　　　　　　　　　　　図3. CCAの学習結果。黒点がノイズを除去した結果
　　　　　　　赤星は未学習データで、青星は問診データから推定した精密検査データの予想値

ちゃんとグラデーション方向に軸が取れてるし、健康状態を表す因子（共通因子）がとれていますね。やったね！また図２とよく似てることからノイズが除去できている思われますね。やったね！問診データから予想した⁸精密検査結果も本来の値と近く、まぁまぁ推定できていますね。やったね！

CCAと他の解析手法との関連

線形モデルをつかった解析手法は固有値問題に帰着できるものがとても多いです。CCAも前節で紹介したように一般化固有値問題に帰着していました。この節では他の線形手法と固有値問題という観点で比較してみます。
比較するために一般化固有値問題を

\begin{align*}
A \mathbf{w} =& \lambda B \mathbf{w} \\
B^{-1}A \mathbf{w} =& \lambda \mathbf{w}
\end{align*}

とおきます。するとCCA含む他の手法は以下のような行列$A、B$における固有値問題を解いていることになります⁹.

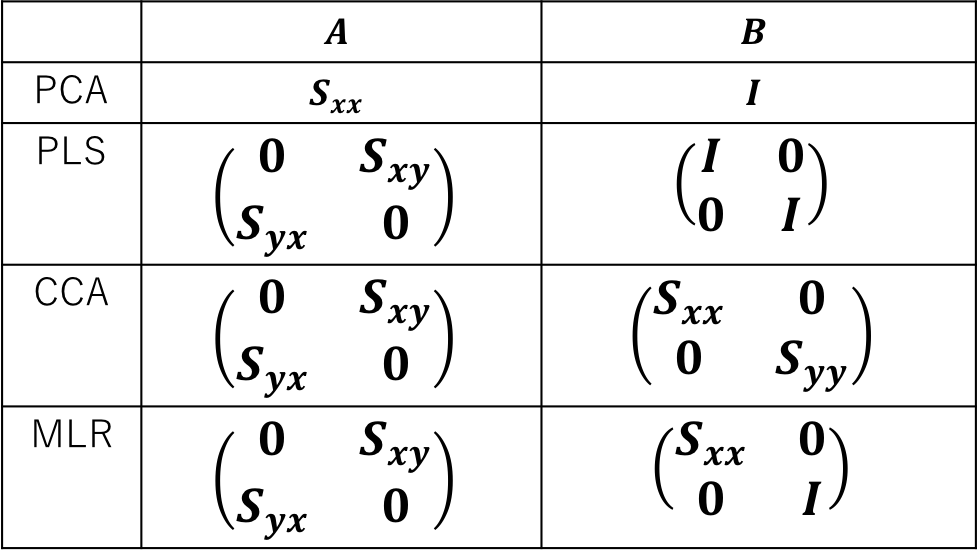
　　　　　　　　　　　　　　図4. 固有値問題に帰着する他の手法との比較

おわりに

この記事を書くにあたって色んな文献を参考にしました¹⁰。なのである意味、今回の記事の内容は調べたらどこにでも出てくるモノになってます。ですが式変形とかを他のサイトより丁寧にやったつもりなのでCCA初学者の手助けになってたら嬉しいです。
また、今回は紹介できませんでしたがCCAによく似た手法としてInter-Buttery Factor Analysis(IBFA)¹¹という手法があります。この手法は全ビューの共通成分だけでなく各ビューの固有成分も同時に抽出できる手法で中々に役に立つ手法です。
IBFAでは以下の等式がなるべく成り立つように線形変換$A_x, A_y, G_x, G_y$を見つけます。

\begin{align*}
\left(\begin{array}{cc}
S_{xx} & S_{xy} \\
S_{yx} & S_{yy} \\
\end{array}\right) = \left(\begin{array}{ccc}
A_x & G_x & O \\
A_y & O & G_y \\ 
\end{array}\right) \left(\begin{array}{cc}
A^T_x & A^T_y \\
G^T_x & O  \\
O & G^T_y  \\
\end{array}\right)
\end{align*}

線形変換$A_x, A_y$が共通因子で線形変換$G_x, G_y$が固有因子になります。
このようにマルチビューデータに対する解析手法は他にもいっぱいあり奥の深い分野なので、興味を持ったら是非、勉強してみてください！！

パッと見、朱鷺の杜にのってる結果と一致していないようにみえるのは、おそらく分散を1に規格化しているかどうかの違いだと思います。 ↩
この記事ではPCAの「主成分（得点）＝データを線形変換した値」に習い、「共通成分＝データを線形変換した値」と呼ぶことにしています。 ↩
CCAでは共通成分間の相関係数が大きくなるように写像（線形変換）を求めるわけですが、求まった写像を使っても同じペア$(\mathbf x_n,\mathbf y_n)$の共通成分が一致する（$u_n = v_n$となる）保証はありあません。ですので「それって本当に共通成分を抽出することになるの？」という疑問は当然起きちゃいます。ですがこの点についてはこの文献が確率モデルをベースに相関係数が最大となる写像を求めることが共通成分（共通の潜在変数）を求めることに帰着することを説明しているのでオススメです。 ↩
人間が視覚やら聴覚など五感を統合して外界を正しく認識しているように、機械学習の力でセンサーから得られたデータを統合して、データの本質を表す因子をみつけましょう（現象を理解しましょう）って感じです。 ↩
大切な情報は全部の計測データに少しずつでも含まれているでしょ！むしろ特定の計測データにしか含まれていない情報は計測器由来のノイズでしょ！って信念のもと、機械学習の力で計測データから共通のシグナルを抽出し、それ以外のシグナルはノイズとして除去しましょうって感じです。 ↩
機械学習の力で計測コストが低い計測データから計測コストが高い計測データを予測しましょうって感じです。 ↩
PCAだと1次元の時は「分散最大化」っていう基準で導出して、2次元以上だと「復元誤差最小化」って基準で導出することが多いですが、CCAもPCAみたいに２次元以上は別の基準で導出できたりできるんでしょうかね？おそらく「ノイズの分散を考慮した復元誤差最小化」って基準で導出できる気がします。 ↩
今回、片方のビューデータからもう一方のビューデータを様子するとき、$\hat{\mathbf y_*} = \mathbf b \mathbf a^T \mathbf x_*$で求めましたが、$u_*$と$v_*$は一致するとは限らないため、予測精度をあげるときは一旦$u_* = \mathbf a^T \mathbf x_*$を求め、$u_*$に対応する$\hat{v_*}$を求めたあと、この$\hat{v_*}$を使って$\hat{\mathbf y_*} = \mathbf b \hat{v_*}$のように予測したほうがいいです! ↩
こちらの文献から引用しました。こうやって他の固有値問題に帰着できる手法と比較している文献はめちゃくちゃ貴重ですね。 ↩
今回の記事は基本こちらの解説記事を参考に作成しています。自分の拙い文章を最後まで読んでくださって感謝しかないんですが、正直、式を細かく追わないのであればこっちを読んだ方がいいと思ってます。なので、この記事を読んでもCCAが分からなかったて方はぜひ読んで見てください。 ↩
IBFAはもともと心理学の分野の手法っぽいです。これが原著ですが、原著以外にアルゴリズムを解説している文献、記事が少なく特に日本語で書かれているものは見つかりませんでした。よかったら誰か書いてください。 ↩