ガウス過程と機械学習3章のノート
- ガウス過程と機械学習を読んだ自分用のノートです。
- 後で見返す用なので、細かすぎることは書かずあらすじ程度の内容。
- 詳しいことは本を買って読んでみてください。
- 誤字脱字、間違いなどが有りましたらコメントよろしくおねがいします。
今回のノートにおける主題:ガウス過程を用いてガウス過程の回帰モデルを作成する。
説明の都合上3.4節を先に説明してから3.3節に入る。
3.4ガウス過程回帰モデル
先にガウス過程を用いてどのように回帰問題を解くのかを議論する。
答えは簡単で入力データを条件とした条件付き確率で解決する。
- $N$個の観測データ
- $\mathcal{D} = {(x_{1},y_{1}),\cdots ,(x_{N},y_{N}) }$
- $y_{n}$ の平均は0になるように平行移動
- $y = f(x)$ という関係がある
- $f \sim GP(0,k(x,x'))$ のガウス過程で得られる。
3.4.1ガウス過程回帰モデル
新しいデータ $\tilde{x}$ に対して出力を ${\tilde{y}}$ 求めたい。
条件付き確率の公式
\begin{align}
p(B|A) = \frac{p(A,B)}{p(A)}
\end{align}
を用いれば、観測データ$\mathcal{D}$ と新しいデータ$\tilde{x}$ を入力したときに
\begin{align}
p(\tilde{y}|\tilde{x},\mathcal{D}) = \frac{p(y,\tilde{y}|x,\tilde{x})}{p(y|x)}
= \frac{\mathcal{N}(0,K')}{\mathcal{N}(0,K)}
\end{align}
\begin{align}
K &= k(x_{n},k_{m})\,, n = 1,\cdots , N \\
K' &= k(x_{n},k_{m})\,, n = 1,\cdots , N+1 \\
\end{align}
で$x_{N+1} = \tilde{x}$ である。
ガウス関数同士の積はガウス関数になることを用いて、うまく平方完成を行うと
\begin{align}
p(\tilde{y}|\tilde{x},\mathcal{D}) = \mathcal{N}\left(\tilde{k}^{T}K^{-1}y,\tilde{\tilde{k}}-\tilde{k}^{T}K^{-1}\tilde{k}\right)
\end{align}
で与えられる。
ここで
\begin{align}
\tilde{k} &= \left(k(\tilde{x},x_{1}),\cdots, k(\tilde{x},x_{N})\right)^{T}\\
\tilde{\tilde{k}}& = k(\tilde{x},\tilde{x})
\end{align}
である。
ガウス過程回帰モデルはベイズ推定であるので、通常の機械学習モデルのような結果($y=f(x)$のようなもの)を得るには予測に対する点推定が必要である。
点推定は基本的に予測分布の平均値を利用する。
\begin{align}
E\left[\tilde{y}\right| \left.\tilde{x},\mathcal{D}\right] = \tilde{k} {}^{T}K^{-1}y
\end{align}
3.4.2 ガウス過程回帰の計算(Python実装)
ここでは「ガウス過程と機械学習」のサポートページをもとにPython3 で実装を行う。
まず必要なライブラリの呼び出し
import numpy as np
# 多変量正規分布の
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt
利用するパラメータの設定
# plot parameters
N = 100
xmin = -1
xmax = 3.5
ymin = -1
ymax = 3
# GP kernel parameters
eta,tau,sigma = [0.1,1,1]
動径基底関数(RDF) を出力する関数を定義。
kgauss(params) は x,x' を代入することで$k(x,x')$が得られる.
def kgauss(params):
[tau,sigma] = params
return lambda x,y: tau * np.exp (-(x - y)**2 / (2 * sigma * sigma))
$k_{} = (k(\tilde{x},x_{1}),\cdots, k(\tilde{x},x_{N}))$
$ \tilde{k} = (k(\tilde{x},x_{1}),\cdots, k(\tilde{x},x_{N}))^{T} $ を求める関数
# xtrain は訓練データ
# \tilde{k} を求める。
def kv(x,xtrain,kernel):
return np.array([kernel(x,xi) for xi in xtrain])
訓練データによって得られる共分散行列を出力する関数.
eta * np.eye(N) は観測誤差($y = f(x)+\epsilon $)から来る項.
def kernel_matrix(xx,kernel):
N = len(xx)
# np.eye(N) は単位行列
return np.array([kernel(xi,xj) for xi in xx for xj in xx]).reshape(N,N) + eta * np.eye(N)
ガウス過程回帰の予想分布(テキストP83, (3.74)式) の平均と分散を出力する関数
def gpr(xx,xtrain, ytrain, kernel):
# 入力データ(xtrain) をもとにガウス分布の分散を求める
K = kernel_matrix(xtrain,kernel)
Kinv = np.linalg.inv(K)
ypr, spr = [],[]
for x in xx:
# s = k**
s = kernel(x,x) + eta
# k = k*
k = kv(x,xtrain, kernel)
# 推定値(平均)
ypr.append(k.T.dot(Kinv).dot(ytrain))
# 分散
spr.append(s - k.T.dot(Kinv).dot(k))
return ypr, spr
プロット用の関数
def gpplot(xx, xtrain, ytrain, kernel, params):
ypr,spr = gpr(xx, xtrain, ytrain, kernel(params))
fig, ax = plt.subplots()
ax.plot(xtrain, ytrain, 'bx', markersize=16)
ax.plot(xx, ypr, 'b-')
# 平均値から ±2 √分散 を塗りつぶす
ax.fill_between(xx, ypr - 2*np.sqrt(spr), ypr + 2*np.sqrt(spr), color='#ccccff')
ax.grid()
plt.show()
# データのロード
train = np.loadtxt("data.txt")
xtrain = train.T[0]
ytrain = train.T[1]
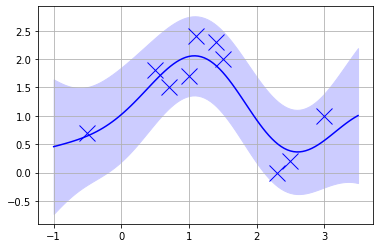
# プロット
gpplot(xx, xtrain, ytrain, kernel, params)
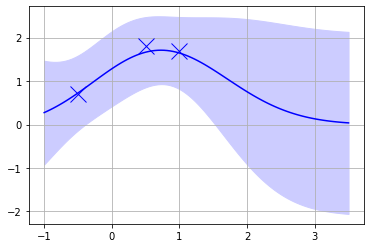
ちなみにデータ点を3つに絞ると、データが得られていない部分の分散が広がっている事がわかる。
xtrain = train.T[0][:3]
ytrain = train.T[1][:3]
gpplot(xx, xtrain, ytrain, kernel, params)
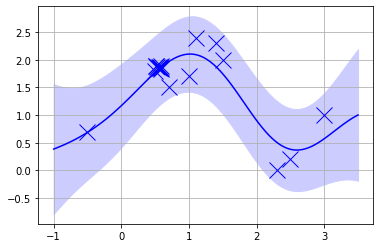
逆に同じ点を10個にかさ増しして学習させても分散の幅は小さくなっていない、つまり過学習があまり起きていない
xtrain = train.T[0]
ytrain = train.T[1]
xtrain = np.append(xtrain, [xtrain[1],]*10 + np.random.rand(10)/10)
ytrain = np.append(ytrain, [ytrain[1],]*10 + np.random.rand(10)/10)
gpplot(xx, xtrain, ytrain, kernel, params)
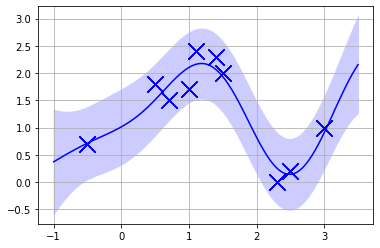
オリジナルのデータを10倍に増やしても過学習は進まず、ある程度分散を残しており、過学習が起きない
xtrain = train.T[0]
ytrain = train.T[1]
xtrain = np.append(xtrain, [xtrain[1],]*10 + np.random.rand(10))
ytrain = np.append(ytrain, [ytrain[1],]*10 + np.random.rand(10)*2.0)
gpplot(xx, xtrain, ytrain, kernel, params)
3.4.3 ガウス過程回帰の計算(Python実装)
ガウス過程回帰の点推定の結果は
\begin{align}
E\left[\tilde{y}\right| \left.\tilde{x},\mathcal{D}\right]
&= \tilde{k} {}^{T}K^{-1}y \\
&= \sum_{n,m}\tilde{k}(\tilde{x},x_{m})(K^{-1})_{nm}y_{n}
\end{align}
で与えられる。学習データの重み付きの和で有ることがわかる.
このような学習データの重み付きの和で与えられる構造はSVMにも似ているが、ガウス過程回帰では重みの学習は行われず単純にデータ点に関するカーネルの逆行列を解析的に求めるだけで与えられていることに注意.
3.3.1 RBFカーネルと基底関数
この節では ガウス過程におけるRBFカーネル VS 線形モデルにおける基底関数 が対応していることを説明している。
線形モデルにおける基底関数として
\begin{align}
\phi_{h}(x) = \tau \exp(-\frac{(x-\frac{h}{H})^2}{r^2})
\end{align}
として、$x\in (-H,H)$ の区間に $1/H$ ごとに等間隔な基底関数を持ってきたとする。
y = w_{h}\phi_{h}(x)
予測でパラメータ$w_{h}$の数は$2H^{2}+1$ となる。
イメージはテキストの3.1節の図3.1(a) のガウス分布が H 個並んでいるという状況.
この線形モデル基底関数の個数を無限大$(H \to \infty)$ とするとRBFカーネルに収束することがわかる。
このことをもとに、ガウス過程モデルは無限個のパラメータを用いて表さた線形モデルと呼ばれる。
3.3.2 さまざまなカーネル
この節で解説されているのは
- ガウス過程で用いられるカーネルは複数種類がある
- 異なるカーネル関数同士の和や積がまたカーネル関数になる
である。
カーネル関数の定義についてこの本ではあまり触れられていないのでPRML などで確認するのが良い。
Martern カーネルの話は微分できる回数が有限回のカーネル関数の例の紹介である。
その他のカーネルの話は文字列、グラフ、木構造などもカーネルとして用いることができる話題でPRMLにも少しだけ記述があるが、正直に言うとどの文献を参考にすればよいのか知らない。
3.3.3 観測ノイズ
観測にノイズがある場合つまり
\begin{align}
y_{n} = f(x_{n}) + \epsilon_{n}
\end{align}
を考える。ここで$\epsilon_{n} $ がガウス分布 $\epsilon_{n} \sim \mathcal{N}(0,\sigma^2)$ に従っているとする。
このとき $y_{n}$ の確率分布は
\begin{align}
p(y_{n}|f(x_{n})) = \mathcal{N}(f(x_{n}),\sigma^2)
\end{align}
となる。