pandas のデータ集約とグループ演算を利用して株価を分析する

データをカテゴライズしてそれぞれのカテゴリに関数を適用するのは集約や変換と呼ばれます。これらはデータ分析のワークフローの中でもとりわけ重要な部分とされます。 pandas はグループ演算における強力な機能を有しており直感的な操作が可能です。

R 言語の様々なパッケージ作者であるハドレーウィッカム氏の有名な論文 The Split-Apply-Combine Strategy for Data Analysis (PDF) ではグループ演算のプロセス「分離ー適用ー結合」について述べられています。 pandas でもこのグループ集約操作モデルをベースとなる考え方として取り入れています。データはプロセスの最初の段階で 1 つ以上のキーによって分離され、次にそれぞれのグループに関数が適用され、関数を適用した結果が結合されて結果を示すオブジェクトに格納されます。

以前に Ruby で日本国内の株価を取得してみました。これで収集したデータを利用して実際の株価に対するグループ演算を操作する例を pandas によって試してみたいと思います。

数社の株価を年毎にグルーピングし関数を適用する

pandas の groupby でグルーピングされた変数は GroupBy オブジェクトになります。 apply メソッドはデータを操作しやすくする断片に分離し、それぞれのオブジェクトに関数を適用した上で結合をします。

# 数社の株価をピックアップ
# NTT データ
stock_9613 = pd.read_csv('stock_9613.csv',
                         parse_dates=True, index_col=0)
# DTS
stock_9682 = pd.read_csv('stock_9682.csv',
                         parse_dates=True, index_col=0)
# IT ホールディングス
stock_3626 = pd.read_csv('stock_3626.csv',
                         parse_dates=True, index_col=0)
# NSD
stock_9759 = pd.read_csv('stock_9759.csv',
                         parse_dates=True, index_col=0)

# 2010 年以降の終値を取り出してひとつのデータフレームにする
df = pd.DataFrame([
    stock_9613.ix['2010-01-01':, '終値'],
    stock_9682.ix['2010-01-01':, '終値'],
    stock_3626.ix['2010-01-01':, '終値'],
    stock_9759.ix['2010-01-01':, '終値']
], index=['NTT データ', 'DTS', 'IT ホールディングス', 'NSD']).T

#=> 日付         データ DTS   IT ホ  NSD
# (中略)
# 2015-01-05     4530  2553  1811  1779
# 2015-01-06     4375  2476  1748  1755
# 2015-01-07     4300  2459  1748  1754
# 2015-01-08     4350  2481  1815  1775
# 2015-01-09     4330  2478  1805  1756
# 2015-01-13     4345  2480  1813  1766
# 2015-01-14     4260  2485  1809  1770
# 2015-01-15     4340  2473  1839  1790
# 2015-01-16     4295  2458  1821  1791

2010 年以降の各社の株価が得られました。さてここにあげた数社は協働することも多そうですが、株式相場においては実際にどれくらい相関があるでしょうか。ここからちょっと好奇心を発揮して、 NTT データ社に対する年次の相関係数を求めてみることにします。

グルーピングされた株価同士の相関係数を求める

# 推移を求める
rets = df.pct_change().dropna()
# 年次でグルーピングする
by_year = rets.groupby(lambda x: x.year)
# 相関係数を計算する無名関数を定義する
vol_corr = lambda x: x.corrwith(x['NTT データ'])
# グルーピングしたオブジェクトに関数を適用する
result1 = by_year.apply(vol_corr)
print(result1)

#=>   NTT データ       DTS        IT ホ       NSD
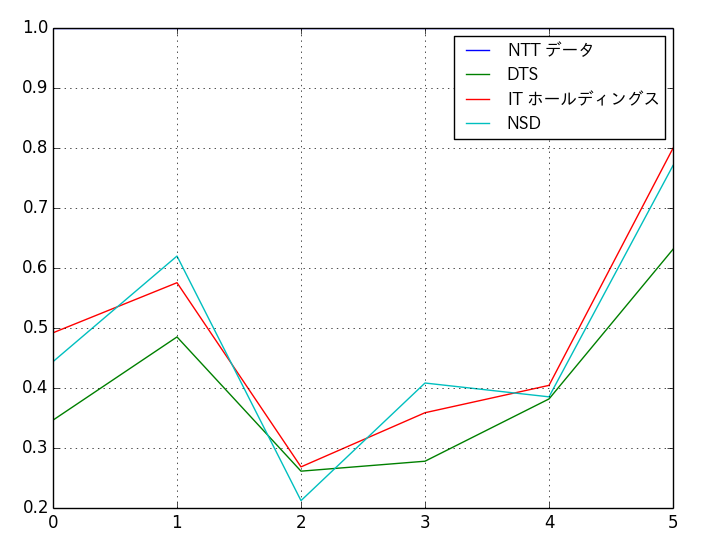
# 2010        1  0.346437     0.492006  0.443910
# 2011        1  0.485108     0.575495  0.619912
# 2012        1  0.261388     0.268531  0.212315
# 2013        1  0.277970     0.358796  0.408304
# 2014        1  0.381762     0.404376  0.385258
# 2015        1  0.631186     0.799621  0.770759

matplotlib で可視化してみましょう。

列と列の間の相関を求めるのも apply メソッドできます。たとえば NTT データに対する DTS 社の株価の相関を求めてみます。

# ある列と他の列の相関係数を求める無名関数を適用する
result2 = by_year.apply(lambda g: g['DTS'].corr(g['NTT データ']))
print(result2)

#=>
# 2010    0.346437
# 2011    0.485108
# 2012    0.261388
# 2013    0.277970
# 2014    0.381762
# 2015    0.631186

少し複雑な関数を定義してグルーピングされた株価に適用する

適用できるのは普通の関数でも同じです。たとえば、最小二乗法 (OLS) による線形回帰をグループごとに求めてみましょう。

# 線形回帰をする関数を自作する
def regression(data, yvar, xvars):
    Y = data[yvar]
    X = data[xvars]
    X['intercept'] = 1.
    result = sm.OLS(Y, X).fit() # 計量経済学ライブラリの線形回帰メソッド
    return result.params # 結果が返る

# 線形回帰する関数をグルーピングされた株価に適用する
result3 = by_year.apply(regression, 'DTS', ['NTT データ'])

#=>    NTT データ  intercept
# 2010  0.313685   0.000773
# 2011  0.509025  -0.000057
# 2012  0.360677   0.000705
# 2013  0.238903   0.002063
# 2014  0.395362   0.001214
# 2015  0.418843  -0.002459

まだ 2015 年については半月経ったばかりですから何とも言えませんが、ひとまずそれぞれの年の結果が求まりました。このようにグルーピングしたデータに関数を適用することで色々な角度から分析を試すことができて大変便利ですね。

まとめ

apply メソッドで関数そのものを適用できるということはさまざまな可能性をひらく扉になります。ここで適用する関数は、オブジェクトまたはスカラー値を戻り値として返すというルール以外は、分析者が自由に記述することができます。

今回の記事のソースコードはこちらです。

参考

Pythonによるデータ分析入門――NumPy、pandasを使ったデータ処理
http://www.oreilly.co.jp/books/9784873116556/