「ADT, 直和・直積, State Machine」

(タイトル字余り)

この記事は筆者が社内勉強会で発表した内容を(個人的に出来が良いと思ったので)外部向けに再構成したものです。(大変長くなってしまった)

状況その1

いきなり以下のコードをご覧ください。

type Contact = 
    {
    Name: PersonalName;
    EmailContactInfo: EmailContactInfo option;
    PostalContactInfo: PostalContactInfo option;
    }

そして以下の仕様をご確認ください。

Business Rule:

• “A contact must have an email or a postal address”

出典と動機、課題

上掲コード及び仕様はDesigning with types: Making illegal states unrepresentable | F# for fun and profitより引用しています。はっきりいって本記事はこの“Designing with types”シリーズのさわり紹介みたいなもんです。原典を読めでもいいのですが、以下の動機により自分でも言語化してみることにしました。(ただ、**原典は読め。**超良いです。)

• Elmなどの関数型言語を推している勢として、代数的データ型、特に直和型という存在に戸惑う初学者がどうも多そうに見える。ので、解説を試みたい
• それらの言語では、(特に静的型付けの場合、)型を使うと「いい感じ」にプログラミングでき、楽しいのだが、そのためのコツとして自分なりに考えていることをついでに言語化しておきたい

元シリーズの著者はF#のエヴァンジェリストな方で、F# for fun and profitはF#公式の学習リンク集でも先頭に来ているとても充実したWebリソースです。¹

引用コードもF#ですが、雰囲気で読めるでしょう。

さて、引用コードは、仕様として挙げたBusiness Ruleを正しく反映しているでしょうか？

可能な状態の数は？

実は引用コードはすでに一段階の改良を経たあとです。

後置optionキーワードはF#でOption(言語によっては同機能をMaybeと呼ぶ)型を作るもの。つまり、「ある型の値があるか、あるいは何もない状態」を表現できるようにする代物です(ときに人類がnullで済まそうとしてしまう、アレです)。ここでは元々optionのなかった項にoptionを適用済みで、したがって「値がない状態」も表現できるように改良済みです。

ここで小問題を切り出します。具体的な値の「中身」は無視し、値が「あるか、ないか」に注目した場合、引用コードにおいて取りうる(可能な)状態の数は何通りでしょうか？

.

.

.

……そう、4通りです。

• Nameは必ず存在するはず(optionなし)なので、変動しうる組み合わせは残りの2項
• EmailContactInfo あり・PostalContactInfo あり
• EmailContactInfo あり・PostalContactInfo なし
• EmailContactInfo なし・PostalContactInfo あり
• EmailContactInfo なし・PostalContactInfo なし

そしてこの状況は、ちょっとマズいのです。

何がマズく、何故そうなるのか

原文を引用すると:

... In this design, it would be possible for a contact to have neither type of address at all. But the business rule says that at least one piece of information must be present.

つまり、「EmailContactInfoなし・PostalContactInfoなし」は仕様からすると不正な状態であり、現状だとデータ構造上は、不正な状態を表現できてしまうという点にマズさがあります。

何故こうなるのでしょう？ それは、EmailContactInfoとPostalContactInfo，2つの項が直交しているからです。互いに独立にあり・なし状態を変更できてしまうのです。

とはいえ、こう考えると思います。「実際の処理としては、そのような不正な状態には陥らないよう実装する」と。

しかし、そう言えるのもこの時点では変動項が2つに過ぎないからです。例えばこれが3つになったら？ 原理的に可能な組み合わせは積で増えるので、8通りになります。8通りすべてOKでしょうか？ 各項のパターンも3通り以上あるかもしれません。3^3なら組み合わせは27通りに膨れます。調査も、不正な状態の防止もすでに相当煩雑になるのは想像に難くありません。

"Making Illegal States Unrepresentable"

この状況を好転させるアプローチを1つ、提案します。Business Ruleをもう少し厳密に噛み砕いてみましょう。引用すると:

… If we think about the business rule carefully, we realize that there are three possibilities:

• A contact only has an email address
• A contact only has a postal address
• A contact has both a email address and a postal address

つまり、「EmailとPostalCodeを省略可能にする」というのは表面的な理解に基づく実装で、「このアプリには3パターンのContact情報が存在しうる」というのがより本質的な理解なのです。だとすれば。それを直截に、簡潔にコードに落とし込めばいいはずでは？ そうすれば実装と仕様との間に差が生じるなどという可能性は生じないはずです。

「不正な状態は、そもそも表現できないようにしてしまえ」ばいいのです！

方法

概念導入します。ここから教科書的な説明が続きます。教科書と言いつつリンクは大抵Wikipediaですが。権威ある解説が欲しい場合は“Types and Programming Languages”(『型システム入門』)などを読むと勉強になりますが、難しい本なので筆者もどこかで力尽きたような記憶。

Algebraic Data Type; ADT, 代数的データ型

ADT「とは何か？」を直球に説明しようとするとなかなか骨が折れます。筆者も自信がないのでしません。英語版Wikipediaの説明を借りて「型を組み合わせて構成される型の一種」と言ってみたところで見るからに情報量に乏しく、悲しくなります。ですので、以下2点を踏まえた上で、以降の項目を読み進めて構成的に姿を捉えてみてください。

• 主に直積型と直和型の組み合わせからなり、
• 状況その1のような対象をコード表現するための強力な武器となります。

関数型言語ならだいたいADTを利用できる印象がありますが、関数型言語でなくても利用できる場合はあります。加えて重要な点として、必ずしも静的型付けでなくても「表現」できますし、その恩恵にあずかることは出来ます。(i.e. Erlang/Elixir)

Product Types; 直積型

まず直積型は、複数の型の、有限個の組み合わせからなる型です。

例えば「整数型の値とブール型の値の組」「整数型の値2つの組」などにあたります。わかりやすい例はTuples; タプルですが、タプルがない言語もそこそこあるのがちょっと説明上ややこしいところです。² よくある例としては、浮動小数点型の値2つの組からなるタプルをPointやCoordinate型と名付けて、³「座標」を表現する、などですね。

タプルの各項(Field; フィールド)に名前をつけることができるものはRecords; レコードといいます。レコードに相当するものならあるという言語は多いでしょう。よく「構造体」とか"struct"の名で呼ばれているデータ構造がそれにあたります。OOPの文脈におけるObject(Classのインスタンス)も、メソッドを同梱するという付加機能がついているというだけで、レコードの一種です。それらOOPにおける付加機能を持たず、静的な値メンバだけを持つObjectをPlain-Old Data Structuresと呼ぶことがあると思いますが、これはまさしくレコードです。

(ちなみに、実装視点だとこの説明はむしろ逆で、まずレコードがあり、タプルは実体としてはレコードで、各項の名前として順序値が暗黙的に自動定義されるもの、となっているケースも有ります。ちょっとすぐに具体名が出てこないので言語実装に詳しい方のコメントを期待します(丸投げ))

(さらにちなみに、実行時の値として、レコードの各項が指定した型の値かどうかは保証されないかもしれないとか、nullが入ってくるかもしれないとかいった議論は、ここでは一旦しません。静的型付けでなくても、null安全でなくても、直積型は直積型です)

Atomicity

直積型は多くの言語に登場するので、すでに受け入れ済みの方が多いかと思います。要は複数の情報・値を1ヶ所(1つの値)に束ねたわけですが、もしnull安全な言語を使用しているならば、このとき追加で意識しておくべきことがあります。それは、

"束ねられたことで、1つの直積型の値は、それを構成する全ての項(メンバ)の値が揃わない限り構築できなくなった"

という「制約」の導入です。

実は状況その1の話の前段として、「『同時に存在しなければならない値の組』があるなら、レコードなどの直積型でまとめよう！」というもありました。まさにこの制約を利用しているわけです。以下に引用すると:

(Designing with types: Introduction | F# for fun and profit)

Creating “atomic” types

… This leads to the first guideline:

• Guideline: Use records or tuples to group together data that are required to be consistent (that is “atomic”) but don’t needlessly group together data that is not related.

2つ以上の値が同時に存在しなければならないのに、独立な変数や、親レコードの独立なフィールドに別々に割り当てられているようなケースでは、やはりどちらかの初期化漏れといったミスが生じがちです。が、null安全な言語で、直積型でそれらを1つにまとめてしまえば、同時に存在していれば構築可能、そうでなければ構築不可能というall-or-nothingな状況を確約できます。複数の値を不可分なものにまとめ、Atomicity(いい訳語がない)を獲得しています。「独立していた項の間に明確な関係性・制約を導入する」という議論の流れを感じてください。

Sum Types; 直和型

("also called"以下の長さに闇を感じさせるWikipedia記事の書き出し)

さて、本記事で最も筆者が労力を割いた節です。

直和型は、定義に並べた有限個の選択肢のうちの、どれか1つであるような型です。各選択肢は専用のTag; タグで明確に区別されます。

• (以前のElmなどでは、このことからTagged Union Typeと呼びます)
• (タグのことをLabel; ラベルと呼ぶ言語や解説もありますが、単なる用語差です)

タグそれだけで値となる選択肢(ただ1つのパターンのみが可能な選択肢)もあれば、タグに任意の型の値を付与できる選択肢も定義できます。後者の場合の付加機能として、定義したタグがそのまま関数として利用可能になり、値構築子(value constructor)となる言語もあります。⁴付与する値は整数やブールなどの単純な型の値でもいいし、レコードなどの直積型を受けとっても構いません。高度な使用法として、「自分自身と同じ型」を受け取るような、再帰的な直和型も定義できます。

さらに、選択肢それ自体が直積型となる、つまり、1つのタグに2つ以上の値を付与できる言語もあります。⁵

(やはり文章だとどうしても飲み込みづらいかもしれません。先に下の方にある、擬似コードによる例を見てきてもいいでしょう)

直和型を「直和」たらしめているのが、なんといってもこの「タグ」です。タグに値が付与される選択肢を考えてみてください。「付与される値の型」を集合と捉えると(e.g. 整数の集合、など)、たとえ複数の選択肢が同じ数・同じ型の値を付与されている状況でも、タグがあることよって明確に集合は「分離されている」と言えます。同じ型でも、タグによってきっちり意味付けされ、別物になっているわけです。

これを言い換えると「共通部分を持たない」ことになり、集合論でいう「直和」(共通部分を持たない和)の性質と合致するわけです。ちなみに、値が付与されない、タグのみの選択肢も、「空集合がくっついてる」と思えば同じです。この性質は、後述する「直和型じゃないやつ」との比較においても重要になります。

• (これを直接反映して、Disjoint Union TypeあるいはDiscriminated Union Typeと呼ぶこともあります)
• (このへん、いささか噛み砕きすぎているとも思うので、よりformalな議論に興味があれば、前掲のTaPLなどを読んでみてください)

OOPでも出てくる用語ですが、ある型の値をタグに付与する(タグで値をくるむ)ことを指してboxingとよく呼びます。逆にタグを剥がして中の値を取り出すことをunboxingといいます。この用語は実行時の挙動について気にし始めるとよく出てきますので、参考に。

直和型の選択肢一つ一つのことは、OCamlなどのML系言語ではvariantと呼んでおり、OCamlでは直和型のことをそのままVariants; ヴァリアント型と呼んでいます。⁶

直和型を自然に表現できる機能を持つ言語では、それら各選択肢に対しパターンマッチできる構文とセットになってることが多い印象です。たとえばcaseだったり、matchだったり。当該構文の中で、各選択肢ごとの処理を行っている部分はBranch; 枝と慣習で呼んだりもします。さらに、値を持つ選択肢に対しては、パターンマッチと同時に付与された値を変数に束縛して取り出せる(destructuringできる)こともあります。

直和型に似たやつ

この節は、地味に重要です。

「列挙型……？」

JavaやTypeScriptのenumキーワードによるもの、Enumerated Typeですね。想起した人も多いのではないでしょうか。

有限個の選択肢により構成される型という点は直和型とかなり近いです。違いは**(実行時に任意に変化できる)値を付与できるかどうか**です。「実行時に任意に変化できる」という但し書きを慌てて付けたのは、例示した2言語の列挙型がいずれも「「値を付与できる」ように見える」機能を伴っているため注意が必要だと感じたからです。例えばJava(SE12)のenumでは、以下のような例が仕様書でも紹介されています:

Coin.java

enum Coin {
    PENNY(1), NICKEL(5), DIME(10), QUARTER(25);
    Coin(int value) { this.value = value; }

    private final int value;
    public int value() { return value; }
}

この例でのCoin型の選択肢はPENNY, NICKEL, DIME, QUARTERの4種なのですが、「定義時に」(n)を付して与えている値は、あくまで定義時(コンパイル時)に定まる定数値⁷で、実行時にはいかなる変更も加えられません。つまりCoin型として有効な値は定義した4種ただそれのみしか存在しません。「Coin型のインスタンスは定義時の4種以外存在しない」とも言い換えられます。仕様にも、

An enum type has no instances other than those defined by its enum constants. It is a compile-time error to attempt to explicitly instantiate an enum type

とあります。

TypeScriptのenumの場合、デフォルトでは定義順と対応した整数値が内部実装(実行時の値)として割り当てられるところを、「任意の文字列値」や、「特定の整数値からの連番」のように指定する、ということが可能になっています。やはりこれらもあくまで定義時に定めるもので、実行時に変化する値ではありません。(用途としては、JSONにシリアライズするときなどに便利そうです)

先に説明した直和型と対比すると、「値を付与できる選択肢を一切使っていないような直和型」は、列挙型と同値と言えます。すべての選択肢がタグのみのものであるような直和型ですね。つまり「直和型があれば列挙型を実現できるが、逆はできない」という関係性になります。

ここで1つ、やっかいなことに、**Rustでは直和型(ないしはそれを包含するADT)を指してenumと呼ぶし、列挙型と訳します。**このことはリンクしたthe Rust bookにも以下のように言及されています:

Enums are a feature in many languages, but their capabilities differ in each language. Rust’s enums are most similar to algebraic data types in functional languages, such as F#, OCaml, and Haskell.

「Union Type……？」

単に "Union Type" と呼ばれている言語機能には注意が必要で、直和型ではないことがあります。

具体的には、ある言語で、型定義/型注釈において**number | string**のような形で定義される型を見たら、それは直和型ではありません。「タグ」を伴わずに、別の既存の型が選択肢として列挙される方式のもの、といったところでしょうか。このたぐいの型に対するちょうどいい用語・訳語が見当たらないのでご存知の方がいたらコメント頂けるとありがたいです。和型……？ 合併型……？

(@recordare さんのコメントより追記: Union Typeの訳として「共用体」という語があるようです。ただし、どのようにメモリ確保されるか、実行時の値の型に応じたタグが処理系によって自動で添付されるかどうか、など、「(メモリ領域の)共用」という訳語の由来が馴染むかどうかは言語依存といえそうです)

Erlang/ElixirやTypeScriptでよく目にするかと思いますが、これらが直和型ではないということは度々言及されています。一見すると名前が似ているので混乱の元なのでしょう。

• Union Typesは直和型ではない | 雑記帳
• Null-tracking, or the difference between union and sum types

名前の上では微妙な違いですが、機能としては**「型に込められる情報」**が変わってくる、全くの別物です。違いの例をいくつか挙げると、

• 直和型でないUnion Typeでは、「同一の型だが意味が異なるもの」を区別することが出来ないのに対し、直和型では別個のタグを付すことで明示的に区別できます
  • 例えば、1つの文字列を引数に取る関数だが、それがファイル名である場合とファイル内容である場合、両方ありうるとき、直和型ならFilename String | FileContents Stringのようにタグで区別可能
• 直和でないUnion Typeは、いわゆるAd-hoc Polymorphism; アドホック多相による関数や演算子のオーバーロードを行っている場合に、型定義として現れます
  • 例えば以下のような例:

function printAnything(value: int | string | bool): void {
  if (typeof value === "int") {
    console.log("The int was ", value);
  } else if (typeof value === "string") {
    console.log("The string was ", value);
  } else {
    console.log("The bool was ", value);
  }
}

TypeScriptには元々このUnion Typeしかありませんでしたが、最近のバージョンでは明確に直和型の性質を持つ型としてDiscriminated Union Typeが利用できるようになりました。ただ、ML族の言語のように、値構築子になるタグや、パターンマッチのような便利な構文はまだないようです。(2019/03現在)

言語ごとの用語

はじめに述べたように、ADTは直和型と直積型(さらに言えばそれらに含まれる整数やブールなどのいわゆるプリミティブな型)から構成されますが、あくまで筆者の印象として、「ADTといえば直和型」と捉えられていることが少なくないように思います。用語の厳密な定義はどこでも面倒な話題です。

Haskellは、公式WikiにAlgebraic Data Typeというそのものズバリなページを持っており、それがSumとProductからなることも含め、本記事の論旨と共通した説明が簡潔にまとまっており、用語の参照点としては妥当なのではないかと思います。

それ以外の言語で、直和型を指す用語をざっとまとめてみると、以下のような具合です。(前出のThe Rust Bookのように、これらが「ADTに相当する」と説明されていることもあります)

• Discriminated Union Type, Discriminated Unions (F#, TypeScript)
• Tagged Union Type, Tagged Unions (Elm 0.18まで)
• Custom Type (Elm 0.19)
• Variant Type, Variants (OCaml)
  • Visual BasicのVariant Typeは別物 (!!)
• Enumerations, Enum (Rust) (!!)

ほかにも専用の語彙を持つ言語もあるかもしれませんが、本記事が区別・理解の助けとなれば幸いです。

代数的データ型の姿

以上を踏まえてElmっぽい擬似コードで示すと、代数的データ型は以下のような姿になります。

(念の為コピペ可能なテキストを)

type PossibleState
    = Initial
    | Activated { count : Int, name : String }
    | Deactivated { count : Int, name : String } { sleepUntil : Time }

社内勉強会で使用した元資料のスクショですが、注釈を付すと以下のようになります:

• 型名としてはPossibleStateで、これが関数・変数の型注釈や他の型の定義内に出現します
• この言語では、{ field: Type }構文でレコードを定義します⁸
• Deactivated選択肢は2種類のレコードを受け取っており、直積型になっていると言えます
  • 「(レコードやタプルなどの)直積型を1種類受け取る選択肢にする」のと、「選択肢自体を直積型にして複数の値を受け取る」のと、どちらがいいかは言語ごとの慣習や個別の状況によります。⁹

状況その1: 改善

満を持して、改善を試みましょう。元のコードを再掲します:

type Contact = 
    {
    Name: PersonalName;
    EmailContactInfo: EmailContactInfo option;
    PostalContactInfo: PostalContactInfo option;
    }

このコードは、

• Option型からなる直交する2つの項を抱えているため、
• 可能だが、仕様上不正な値が表現しうる、

という問題を抱えていたのでした。しかし！ 今なら我々はADT(特に直和型)という武器を知ったわけですので、新たに以下のように実装することが出来ます:

type ContactInfo = 
    | EmailOnly of EmailContactInfo
    | PostOnly of PostalContactInfo
    | EmailAndPost of EmailContactInfo * PostalContactInfo

type Contact = 
    {
    Name: Name;
    ContactInfo: ContactInfo;
    }

• ContactInfoは1つの直和型で、
• (F#構文)各選択肢はofキーワードで指定した型の値を付与され、
• (F#構文)複数の値が付与される選択肢(EmailAndPost)は、*で型が並び、直積型となっています。

ここで、前掲の「本質的な仕様理解」を思い出してください:

• A contact only has an email address
• A contact only has a postal address
• A contact has both a email address and a postal address

見てください！ ContactInfo型はこの3行をド直球にコードで表現しているではありませんか！

不正な状態である「EmailContactInfoなし・PostalContactInfoなし」がそもそもコード上から消滅したのです！当然その状態に陥ることは原理的になくなるわけですので、我々はいわば起きる前にバグを直しました！

「4 → 3の法則」

この節は私見です。

アプリケーション実装を進めていくと、往々にして今回の状況のような、「二値的な状態項が徐々に増えてくる」という現象が発生するでしょう。念の為繰り返すと、Option(Maybe)型の場合は付与される実行時の値によって実際には無限の状態が有り得ますが、あくまで値の「有無」に着目して「二値的」と言っています。ブール型の場合は文字通り二値ですね。

1つの直積型のデータ構造(レコード、オブジェクトなど)の中に、それら二値的な項が「2個発生した瞬間」が、「型脳」を働かせる最初のポイントではないかと感じています。まさに今回のような例がそれです。

二値状態表現型が2つ直交するとき、これまで見てきたとおり$2^2 = 4$通りの可能な状態が発生することをまず心得ます。すると経験上、そこそこの割合で4つのうち1つが明らかにアプリケーション内部で意味を成さない・正しくない・処理を続けられない状態となりがちだったりするわけです。よくあるのが今回の例のような「なし・なし」とか、「False, False」とかいったパターンでしょう。(もちろん、それらが業務上正しいケースもあるので、前掲の思考プロセスの通りbusiness ruleを本質的に把握するよう努めるのが大前提です)

この「1つ」を除去し、可能な4つから正しい3つに集約して、原理的に不正な状態をなくすことを意識するとプログラムがいい感じになるという感覚、あえて名付けるなら「4 → 3の法則」。これが筆者の中に1つの有用な経験則として確立しつつあったところで、今回出典とした"Designing with types: Making illegal states unrepresentable"がまさしくそれを丁寧に解説してくれていました。本記事をまとめようと思った1つの契機でもあったので、付け加えておこうと思います。

ここまでのまとめ

• 「可能な状態の数」と「正しい状態の数」には往々にして差が生じがち
  • 単純に必要な状態項を直交に追加していくと、「可能だが不正」な状態が発生する
• 直和型・直積型を利用できるならば、うまく使って不正な状態を排除しよう
• お題目は: "Make Illegal States Unrepresentable!"

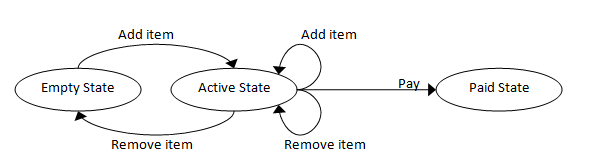
状況その2

コードはだいぶ複雑になりますが、なんとなく分かればOKです。

type ActiveCartData = { UnpaidItems: string list }
type PaidCartData = { PaidItems: string list; Payment: float }

type ShoppingCart = 
    | EmptyCart  // no data
    | ActiveCart of ActiveCartData
    | PaidCart of PaidCartData

let addItem cart item = 
    match cart with
    | EmptyCart -> 
        // create a new active cart with one item
        ActiveCart {UnpaidItems=[item]}
    | ActiveCart {UnpaidItems=existingItems} -> 
        // create a new ActiveCart with the item added
        ActiveCart {UnpaidItems = item :: existingItems}
    | PaidCart _ ->  
        // ignore
        cart

let makePayment cart payment = 
    match cart with
    | EmptyCart -> 
        // ignore
        cart
    | ActiveCart {UnpaidItems=existingItems} -> 
        // create a new PaidCart with the payment
        PaidCart {PaidItems = existingItems; Payment=payment}
    | PaidCart _ ->  
        // ignore
        cart

出典と概略

今回はDesigning with types: Making state explicit | F# for fun and profitからの引用になります。

まず、最初のコードブロック内、直和のShoppingCart型でショッピングカートを表現していることが見て取れます。

さらに。新しく関数が出現しました。addItemやmakePayment関数で、ShoppingCart型の値に対する操作を定義しています。特に関数に対しどんな値を受け取るかといった型注釈がありませんが、match式で各選択肢に対しパターンマッチしているらしい、ということから感じ取ってください。(F#は静的型付けですがコンパイラによる型推論があるので、型注釈は必須ではありません)

これら操作関数の中では、当該操作が行えないような選択肢の場合は何もしない、という実装を、直和の選択肢に対するパターンマッチで簡潔に与えることができていることがわかるでしょう。

また、ここでいう「操作」は、入力値に応じて**「新たな状態」である同じShoppingCart型の新たな値を発行して返却**する、というものになっていることに注目してください。(何もしない枝に関しては、元の値をそのまま返却という実装です)

.

.

.

……頭の中に、「状態遷移」という単語が浮かんだ方もいるのでは？

(Finite) State Machine; (有限)状態機械

このような形式化の枠組みにはぴったりの名前がかなり昔から¹⁰存在しています。

それこそが**(Finite) State Machine; (有限)状態機械**です。Finite State Automaton; 有限状態オートマトンとも呼びます。

ちょっと難しく言うと、物事を(離散)数学的に捉え、計算・表現可能にするための形式化(モデル化)の一手法です。

対象とする物事、「系」を、

• 独立し、ある時点ではある1つの選択肢のみを取りうる「State; 状態」の集合と、
• 状態に対する「Input; 入力」の候補、および、
• 入力と、元の状態に応じて決定される、次の状態への「Transition; 遷移」で記述する手法です。

この説明を元に、状況その2のコード例を再度振り返ってみてください。

まず、直和型で表現したShoppingCart型は、まさに

独立し、ある時点ではある1つの選択肢のみを取りうる「State; 状態」の集合

これに当たります。次に、addItem関数が第2引数で受け取っているitemや、makePayment関数の第2引数のpaymentは、

状態に対する「Input; 入力」の候補

に当たるでしょう。だとすると、それら関数(例えばaddItem)が入力(item)と元の状態(cart)に依存して、次の状態(新しいShoppingCart型の値)を返していることは、

入力と、元の状態に応じて決定される、次の状態への「Transition; 遷移」

ですから、まさにState Machineの説明そのものです！

そうです。状況その2でやっている、「可能な状態(とパラメータ)を列挙」「入力と直前の状態に依存する関数で操作を定義」、これらは**State Machineによる対象の形式化(モデリング)**にほかなりません！

以下のような、状態遷移図を見たことのある方も多いのではないでしょうか。

物事をState Machineとして捉え、その上で状況その1と同様、ADTを用いてそれをコードにそのまま落とし込めるのです。

そして、世の中にはState Machineとして捉えると思いの外しっくり来る物事が多かったりします。ElmでWebアプリケーションを書いていると強く感じますが、GUIなんてのは最たるもので、ひたすらState Machineですね。

State Machine Thinking

少なくとも筆者の経験上、様々なレイヤのアプリケーション開発において、State Machineを使った考え方は非常に役に立ちます。¹¹物事をすっきり、かつはっきりと定式化出来ます。State Machine Thinkingと呼んでみましょう。

State Machineを使う利点が、Designing with Typesには以下のように述べられています:

• Each state can have different allowable behavior.
  (個々の状態が別々の許可された振る舞いを持つことができる)

• All the states are explicitly documented.
  (すべての状態が明示的に書き下される)

• It is a design tool that forces you to think about every possibility that could occur.
  (全ての起こりうる状態について考えることを『強制』する設計ツールである)

このうち、特に3点目、「全ての起こりうる状態について考えることを『強制』する」というのは見逃せないポイントです。我々はプログラミングにおいて多くのことをサボりがちです。エラー処理、バリデーション、etc... 怠惰はプログラマの美徳といいますが、誤解してはいけません。全体として最小の労力になるように努力を惜しまないこと(The quality that makes you go to great effort to reduce overall energy expenditure.)こそが本質なのですから、後で問題になるかもしれない物事に注意を払うことを促してくれる道具は最高に有用です。

特に静的型付けによるコンパイル時検査がこれに加わると、「エラーハンドリングをサボる」「特定条件の実装を忘れる」といったたぐいのミスの可能性を実行前に刈り取ってくれます。最初は難しく感じるかもしれませんが、慣れれば優秀な指導教官が常についているような状態になりますから、逆に非常に快適になります。プログラミングにおける「楽しさ」を感じられること、請け合います。

今日からあなたもState Machine Thinking!!

使い時と、「使うべきでない時」

と、このように調子よくState Machineを勧めて、読者のState Machine使いたい欲を高めたところで、最終章へ向かう前に一旦水を差しておくことにします。というのも、何事もそうであるように「どんな状況でもかならず使うべきもの」ではないことも確かだからです。State Machineによるモデリングは、場合によってはプログラムを複雑にする割に、得るものが少ないかもしれません。

State Machineを使うのが良い時というのは、例えば以下のような条件が揃ってくるときです:

• You have a set of mutually exclusive states with transitions between them.
  (相互に排他的な状態の集合と、状態間の遷移がある)

• The transitions are triggered by external events.
  (外的なイベント(=入力)によって遷移が発生する)

• The states are exhaustive. That is, there are no other choices and you must always handle all cases.
  (状態を網羅的に列挙でき、かつすべての場合を適切に処理する必要がある)

• Each state might have associated data that should not be accessible when the system is in another state.
  (各状態が対応するデータを保持し、しかも異なる状態間ではそれらのデータは互いに独立しているべき)

• There are static business rules that apply to the states.
  (それぞれの状態に適用される、静的なbusiness rulesつまり仕様・業務要求が定まっている)

これらを裏返せば、「状態と言えるような項目はあるが、それに依存して変化するような仕様は別にない」とか、「状態遷移の規則が、コードに反映できるよりも早いスパンで、あるいはユーザによって任意に、動的に変化するシステムである」とかいった場合、その部分にはState Machineは馴染まないということが言えそうです。

状況その2: 未解決問題

では最後に、状況その2が、踏み込んで言えば直和型と関数によるState Machine実装が抱える発展的な課題について触れてこの記事を終えたいと思います。

この章の内容に関しては、Designing with typesシリーズで直接触れられている内容ではなく、筆者が最近関心を持っている内容になります。回答があるわけではないので、未解決問題です。

直和型で表現したState Machineに「欠けているもの」

状況その1を思い出してください。直和型による実装は、最初から不正な状態が存在しない、必要な状態を過不足なく記述したものである点が優れていました。状況その2でのShoppingCart型も、その点に関しては満たしていると言えるでしょう。

一方の状態遷移関数の方はどうでしょうか。

let addItem cart item = 
    match cart with
    | EmptyCart -> 
        // create a new active cart with one item
        ActiveCart {UnpaidItems=[item]}
    | ActiveCart {UnpaidItems=existingItems} -> 
        // create a new ActiveCart with the item added
        ActiveCart {UnpaidItems = item :: existingItems}
    | PaidCart _ ->  
        // ignore
        cart

例えばこのaddItem関数は「買い物」という系においてカートに商品を追加するという行為(入力)をコードにしたものと言えます。支払い済みのカートに商品を追加するというフローはこの系には存在しない、想定しないものですから、コードでは何もしない(// ignore)という処理になっていますね。

存在しない、想定しない行為に対する処理を、内容上何もしてないとはいえ、「記述」しているわけです。

.

.

……これは状況その1で問題視した点と似たような弱点を抱えているのではないでしょうか？ 状況その1では、「不正な状態も表現できてしまうデータ構造」を問題としました。それを改善してきたのでした。今ここでは、「不正な状態遷移も記述できてしまう可能性がある」のです。

だってそうですよね。Business Rulesを理解して「この枝は対応する正しい操作規則が存在しない部分にあたるので、何もしない」と実装することは出来ますし、それは正しいでしょう。が、いつでもそのように正しく実装できるとは限らないじゃないですか？ 状態がもっとたくさんあって、matchの枝が大量にあったら間違えるかもしれませんよね。単純にBusiness Rulesを誤解してしまうことだってありえます。目が疲れていることだってあるはずです。

(Can We) Make Illegal State Transitions Impossible?

直和型によって不正な状態を排除するテクニックは、不正な状態に陥ってしまうようなコードをそれ以降実装者が書いてしまう可能性を排除していた、とも言えます。つまり未来の実装者をエンバグから守るテクニックの1つです。しかし、現状では「不正な状態遷移を記述してしまうかもしれない」という可能性に対する防衛術に欠けています。

「不正な状態遷移をそもそも(実装)不可能にする」ことは出来ないでしょうか？ 言うなれば"Make Illegal State Transitions Impossible"を達成する手段はないのでしょうか。これが次なる大きな課題で、筆者は大変興味を抱いています。これに対するいくつかの手法案を提示して、終わりとします。

案1: 隠蔽とAPI化

この問題に対し、限定的な解決策に過ぎないものの、一般的に用いられている手法として隠蔽とAPI化があります(特にこういう用語としてまとまっているわけではありません)。内部実装の可視性を制御できるモジュールシステムがあることが(おそらく)前提とはなりますが、有用かつ推奨できる手法です。

そもそも不正な遷移が記述できてしまうのは、選択肢が見えているからです。見えているものを無視させてくれないのがState Machineモデリングの有用かつ無慈悲なところですからね。まずこれを見えなくしてしまえばそもそも処理を記述できません。外部から「ShoppingCart型である」ということはわかっても、その中身がどう実装されているかはわからない、という仕組みがあれば、不正な状態遷移を導入されるのを防ぐことができそうです。

**Opaque Data Type**がこのために利用できます。(例によっていい訳語を知らない。不透明型……？)「おぺぃく」と読みます。「不透明」の意味の通り、型自体の存在は外部に公開するものの、型の内部実装(直和型なら選択肢一覧)は公開しない、という仕組みで、多くの言語が持っている機能です。大体の場合module; モジュールという単位で可視性を区切ります。これを使って「状態一覧」を隠してしまいます。

その上で、正しい、許可された振る舞いのみを含む関数を、外部向けのAPIとしてモジュールから公開し、全ての状態遷移はこれらのAPIを通じて行ってもらうようにしましょう。これならBusiness Rulesに則った状態遷移だけが可能となるわけですから安全・安心です。

とはいえ、はじめに限定的な解決策に過ぎないと書いたとおり、この手法は(現実的かつ重要ですが)、肝心の状態遷移APIを実装する際のミスを防いではくれません。State MachineをOpaque Typeとしていたとしても、当該モジュールの内部実装からは当然全ての状態選択肢が見えますから、意図しない遷移の記述が未だ可能です。

案2: 許可された遷移先を幽霊型で表現！？

これはElmフォーラムで議論されていたもので、面白くはあったのですが、幽霊型自体がさらに発展的な内容になってしまう上にコードの複雑化が激しいので、結局実装ミスを全体として減らす方向には働かない可能性が高そうに思います。興味のある方のためにリンクだけ載せておきます。

• Can phantom types be used to restrict the possible transitions in a state machine?
• Making impossible state transitions impossible (Oslo Elm Day question)

最近になっていきなり出てきたアイデアとも思えないので、より古い記事や論文などもあるかもしれません。

案3: Formal Methods; 形式手法！？

State Machineでモデル化された系はFormal Methods; 形式手法による仕様記述と検証の適用例の1つです。さあ、不正な状態遷移がないことを数学的に証明しましょう！(吐血

ほぼ冗談で書いてますが、例えばetcdなどで利用されているRaftアルゴリズムには実際にformal specが存在します。夢物語ではないのかもしれない。実装も生成されてほしい！

むすび

• ADT/直和型の利用から発展して、アプリケーションの対象事物をState Machineとしてモデル化できることに気づく
• State Machineは「起こりうること全て」に考えを及ばせてくれる強力な設計ツール
• みんなもState Machine Thinking!!
• 発展課題: (Can We) Make Illegal State Transitions Impossible?

付録: Q&A

社内勉強会で発表した際の質疑応答をせっかくなのでまとめておきます。

Q. Erlang/ElixirでADT/直和型ってどう書くの？

A. 前提として、Erlang/Elixirは静的型付けでないので、直和型を利用したとしても、例えばパターンマッチの網羅性検証だったりといった機能はついてきません(ベストシナリオでは、dialyzerが指摘してくれるかもしれない。けど、望み薄)。もちろん、的確なモデリングのためには依然有用です。

記述自体はタグとしてatomを使います。値を持つ選択肢は、第一要素にatomを持つtupleで表現するのが一般的です。Erlangのrecord(実行時にはtupleになる)や、Elixirのstruct(実行時にはmap)を使うというのも考えられると思います。例えば、

-type result(Var) :: {ok, Var} | {error, binary()}

これはErlangで書いた直和のresult型で、これに類するものは頻繁に利用されています。

Q. 「直和じゃないUnion Type」に利点はあるの？

A. 「利点」というのはちょっと難しいのでバシッと答えられる方のコメントを期待したい。。。

既存の型をタグ付けせず(boxing/unboxingせず)そのまま扱うので、実行時には効率がいいかもしれません。ただ、実行時の型をもとにfunction dispatchする実装についてはまだしも、(文中で例示されたString型を区別するケースのような、)関数内部で実際になにか処理を行ってみて分岐するような実装ではむしろ効率が悪いこともありそうで、ケースバイケースでしょう。(特にIOが絡む操作をやってみないとわからない、といった場合は直和型に直して事前分岐したほうが効率良さそう)

JS => TypeScriptのように、もともと直和型のない言語に漸進的に型付けする過程では「必要」であるのは間違いないです。

Q. データベースやJSONなど、直和型に対応していないフォーマットとの界面が問題で、導入の壁だよね

A. 全くそのとおりで、そのために多くの人がつらい思いをしていると思います。

JsonSchemaには直和構造を表現できるoneOfがありますが、Web開発でよく持ち出されるSwagger 2.0はoneOfに非対応、最近のOpenAPISpec 3.0はoneOfに対応しているものの関連ツールがまだ未成熟、など(2018年でだいぶ進んだかも？)。

Protocol Bufferでは対応していてほしいなあと思って調べたところ、2.6以降はoneOfがあるようです。

直和型のシリアライズ方法の参考としては、RustのSerDe crateのドキュメントがよくまとまっています。

Q. 直和型にしてプリミティブ型をタグで包むんだけど、実行時挙動としてはプリミティブ型と同じになるような仕組みはある？

A. 賢い言語・コンパイラだと、特に「単一選択肢の直和型」¹²については、実行時にboxing/unboxingが発生しないバイナリorバイトコード等を吐いてくれることがあります。とはいえその場合にもコード上はunboxingを明示的に書かなければならないかもしれません(Elm 0.19で導入されたunboxingはこのパターンです)。
発展して、Haskellならnewtype, Scalaならtagged typeといった更に便利なやつもあります。(別の型としてちゃんと検査器に区別されるんだけど、実装上はまるでプリミティブ型のように扱えて、unboxingをいちいちしなくてよかったはず)

一方、複数選択肢がある直和型の場合は実行時にも識別子が不可避的について回るはず(直和型で書かない場合に必要となる分岐処理に相当する部分)ですが、この辺の細かい実装は言語ごとに様々で、筆者もあまり詳しくないです。

Q. 直和型を「絞り込み」したい、みたいなケースが実装してるとよくあるんだけど、どうにかならない？

具体的には、特定の処理を経たあとは限られた選択肢のみに収束するので、そこから先はそれらに対する処理のみを別モジュールで実装したい、など

A. 全く同感です。よくある状況として、別モジュールでも同名タグを使い回したり、混同を避けるために単に頭文字を付与したり、委譲先モジュールの型に値を移し替えたりなど、ボイラープレートが増えて辛いところだと思います。

なにかいい感じの言語機能があって欲しい気がします。既存のものは思いつかないけど、Haskellならいろいろあるのでなにかありそう。

1. F# (F Sharp)自体はは.NET向けにコンパイルされるML(Meta Language)系の関数型言語です。有名なパイプライン演算子|>の初出です。筆者はF#を書いたことはありません。 ↩

2. ちなみにTupleは本来「テュープル」と発音するので、英語のカンファレンス動画などを聞いているとかなり戸惑うところでもあります。 ↩

3. ある型に、単に便宜上の「別名」を付けるだけの機能は type alias と呼ばれ、これも関数型言語を中心に広く利用できるものです。 ↩

4. この説明がサラッと流されていたり端折られていたりするために、直和型がよくわからなくなるケースがままある印象です。コード例などで直和型の定義に並んでいたものが、その後のコードの中でまるで関数のように使われていた場合、このことを思い出して「ああ、この言語では直和型のタグがそのまま構築子として使えるんだ」と理解しましょう。 ↩

5. 直前で述べた、タグがそのまま値構築子となる言語の場合、このケースではタグは2引数以上を受け取る関数として機能するでしょう。 ↩

6. 不都合なことに、Visual Basicにも全く同じ名前のVariant Typeという型が登場しますが、VBのそれは(筆者はあまり詳しくないのですが)いわゆるAny型に近い代物で、ADTとは全く別物のようです。 ↩

7. この値は単純にアクセサメソッドを経由してPENNY.value()のように取り出せますので、例えばコインの種類に対応する額面が数値で必要な場面で使うなど、自由に利用できます。 ↩

8. 単一のフィールドしか持たないレコードはアンチパターンとされることもありますが、フィールドの追加が予定されている場合など、実務的にはたまに見受けられます。 ↩

9. ただし、「幅の大きすぎるタプルを作ると、それぞれの値の意味が不明瞭になって可読性が下がる」というよく知られたアンチパターンがあり、同様の議論が直積型選択肢にも当てはまります。よって、「単一のレコードを受け取る選択肢」にしておいて、中に入れるレコードを別に用意するのが長期的にはベターであることが多いでしょう。**が、絶対ではないです。**とはいえ、たとえばElmでは、0.19でタプルの最大幅が3までになり、Custom Typeの選択肢にも同様の制約を課すべきか、という議論もなされていたりします。 ↩

10. 決定的に用語を定義した原著がどれかまでは調べませんでしたが、Wikipedia起点でざっと見た感じだと1950年前後には論文がありそう？ ↩

11. なんなら、Statefulなプロトコルなど、そもそも仕様書からしてState Machineを使って説明されているものもあります。一例を上げると、インターネットの根幹部分の1つであるルーティングプロトコル・Border Gateway Protocol 4 (BGP4)を定義しているRFC4271にはFinite State Machineによる説明が与えられています。 ↩

12. 単一選択肢の直和型は、プリミティブ型に意味を持たせつつ、しかも静的型検査が効くようにする手法で、よく使われます。 ↩