野球×データサイエンス

はじめに

この記事は野球のピッチャーを機械学習を使って4つのグループに分類してみた記事です。
記事の中に間違っている点などあると思いますが、コメントなどで指摘していただけると嬉しいです。
記事に関してはできるだけわかりやすいように書いたので楽しんでいただけると嬉しいです。

方針

今回はK-means法という手法を使ってピッチャーを4グループに分けた。
K-means法に関しては後述してある。
参考にしたのは下記の記事である。
大変わかりやすかったので、ここに感謝を申し上げたい。
https://qiita.com/maskot1977/items/34158d044711231c4292

K-meansクラスタリングとは?

クラスタリングとはグループ分けを行うことである。
そのうちの一つの手法にK-means法というものがある。
簡単にK-means法について説明する。
まず学校で先生から近くの生徒と4班に分かれてくださいと言われたとしよう。
クラスを2次元平面として考え生徒のいる場所を2次元平面の座標として考える。
一般的に生徒間の距離が短い人同士でグループを作成すると思う。
距離が短い人同士で指定された数分グループを作成するというのがK-means法のイメージになる。（厳密には距離に関してたくさん種類がある）
そして距離の定義を2次元だけではなく3次元、４次元で考えていくことでグループ分けをしていくのである。（4次元以上になるとグラフは書けない)

データ

何はともあれ機械学習にはデータが必要である。
今回は2019年の日本のプロ野球ピッチャーのデータを使用する。
下記のウェブサイトからデータを入手した。
https://baseball-data.com/19/stats/pitcher2-all/era-5.html

ピッチャーの対称は規定投球回の1/3以上投げたピッチャーとした。（プロ野球には規定投球回というのがある）
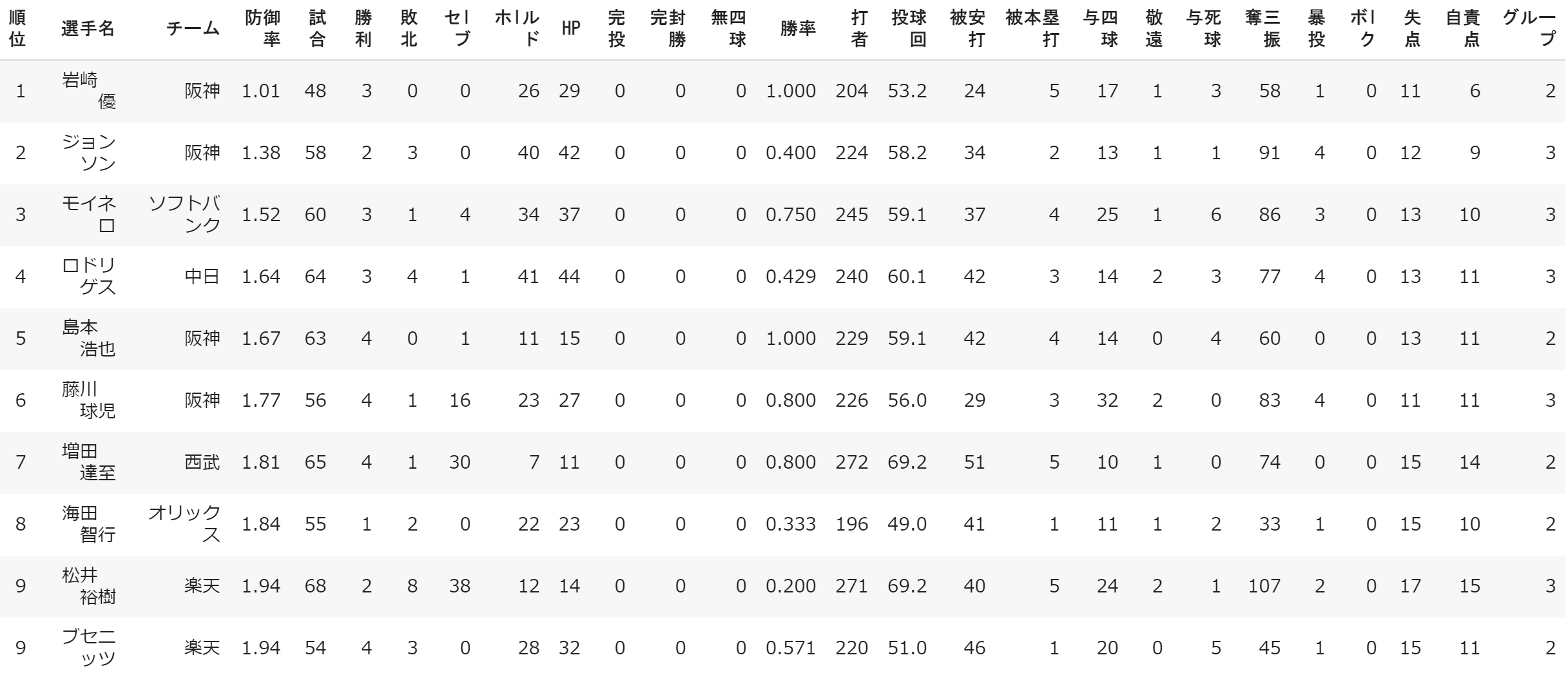
そこから入手したデータが下記のようになった。（順位は防御率の順位）

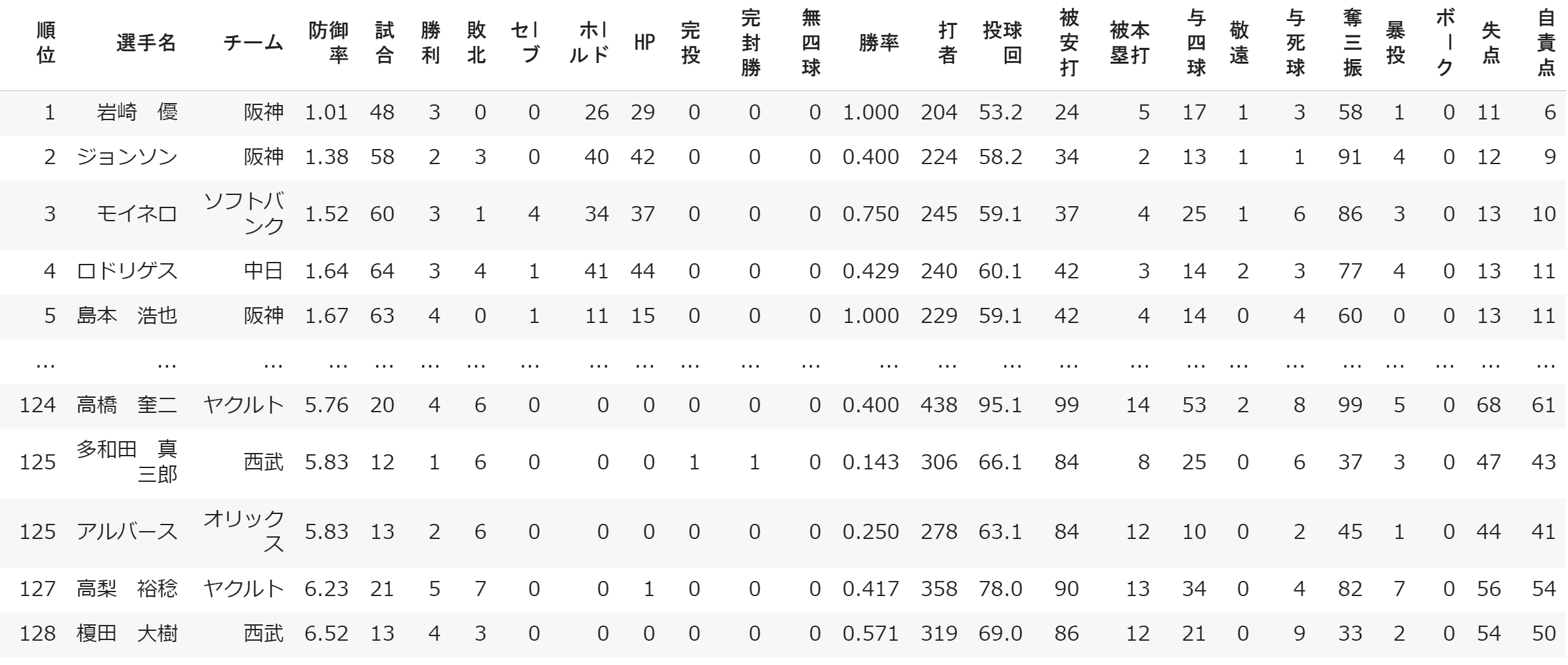
データ前処理

クラスタリングを行う前に変数を絞り、単位変換を行う必要がある。
まず、使用する変数はピッチャーの実力が主に影響を与える、被安打、与四球、自責点、奪三振の４変数を利用する。
さらに各選手を比べるとき、投げている回数が違うので三振の数などを比べるのでは正しく比べることができない。
よって今回はこの4変数を投球回で割ることとした。
これ以降、被安打、与四球、自責点、奪三振の数字は2019年の投球回数で割った値とする。
その処理を行ったものが下記のようになった。（名前は省略）

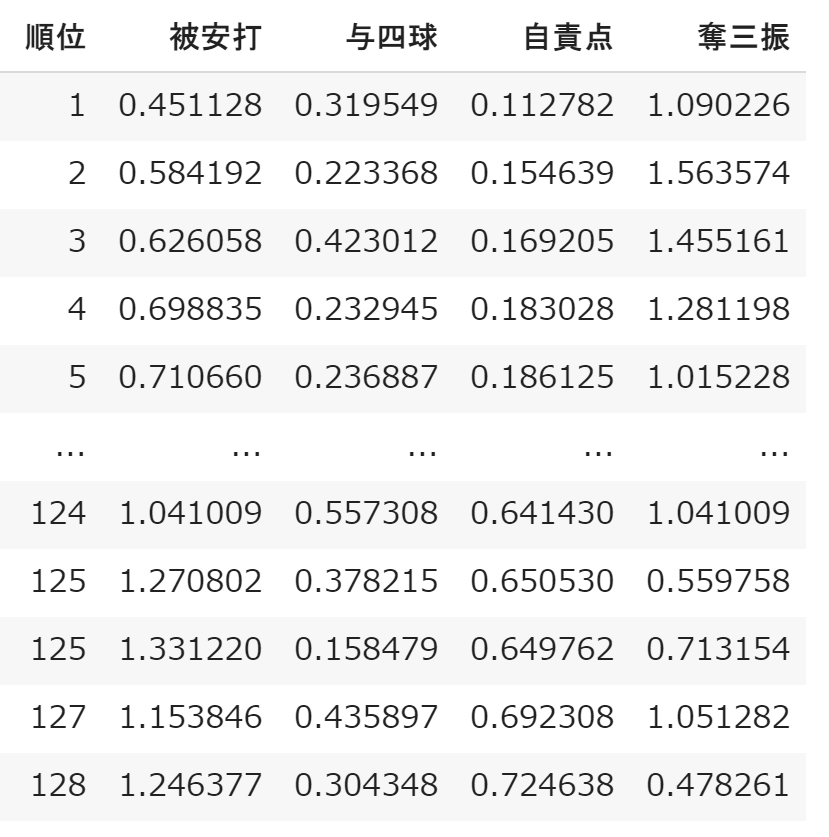
事前分析

クラスタリングを行う前からわかることを簡単に分析していきたいと思う。
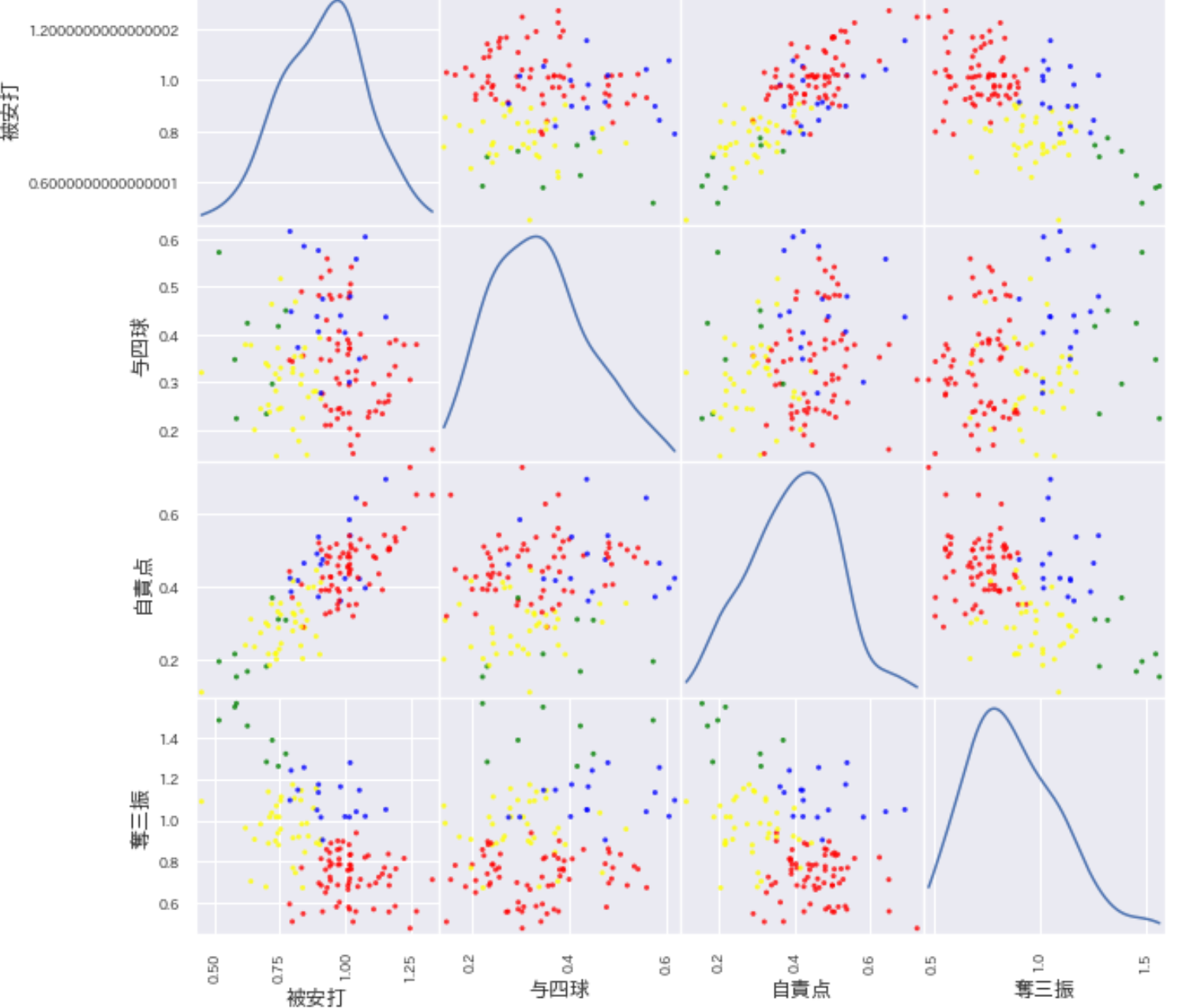
下記のグラフは4変数のうちの2変数の散布図の集まりである。
対角線は値の分布のグラフである。

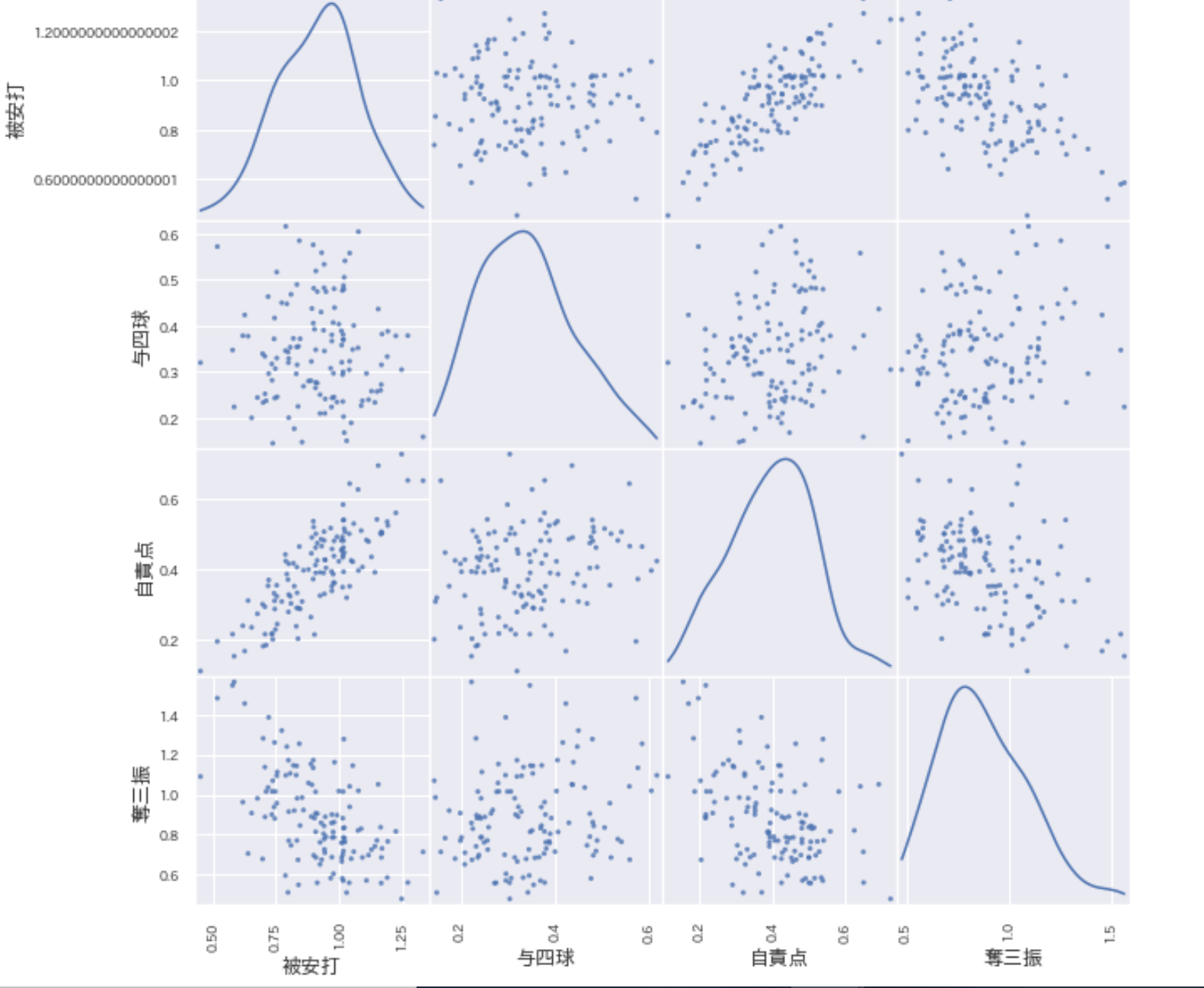
散布図を見てみると三振を取っているピッチャーは被安打数が少ないなどの相関関係がわかる。
新しい発見だったのは与四球の数と被安打数の相関はこのグラフを見る限りだとみえないということだ。

#nK-means法
それではこの記事のメインであるK-means法を行った結果を説明、考察していきたいと思う。
ピッチャーの4変数に対してK-means法を用いて4つのグループに分けたものが下記のグラフである。
下記のグラフは先ほどの散布図を色でグループ分けしたものである。

今後はこの赤(0)グループ、青(1)グループ、黄色(2)グループ、緑(3)グループという単語を使用して考察などを書いてく。
()の中の数字は色に対応した数字で今後赤グループを分析の都合上0グループと呼ぶ場合もある。
このグラフからうまく4つのグループに分けれたことがわかる。

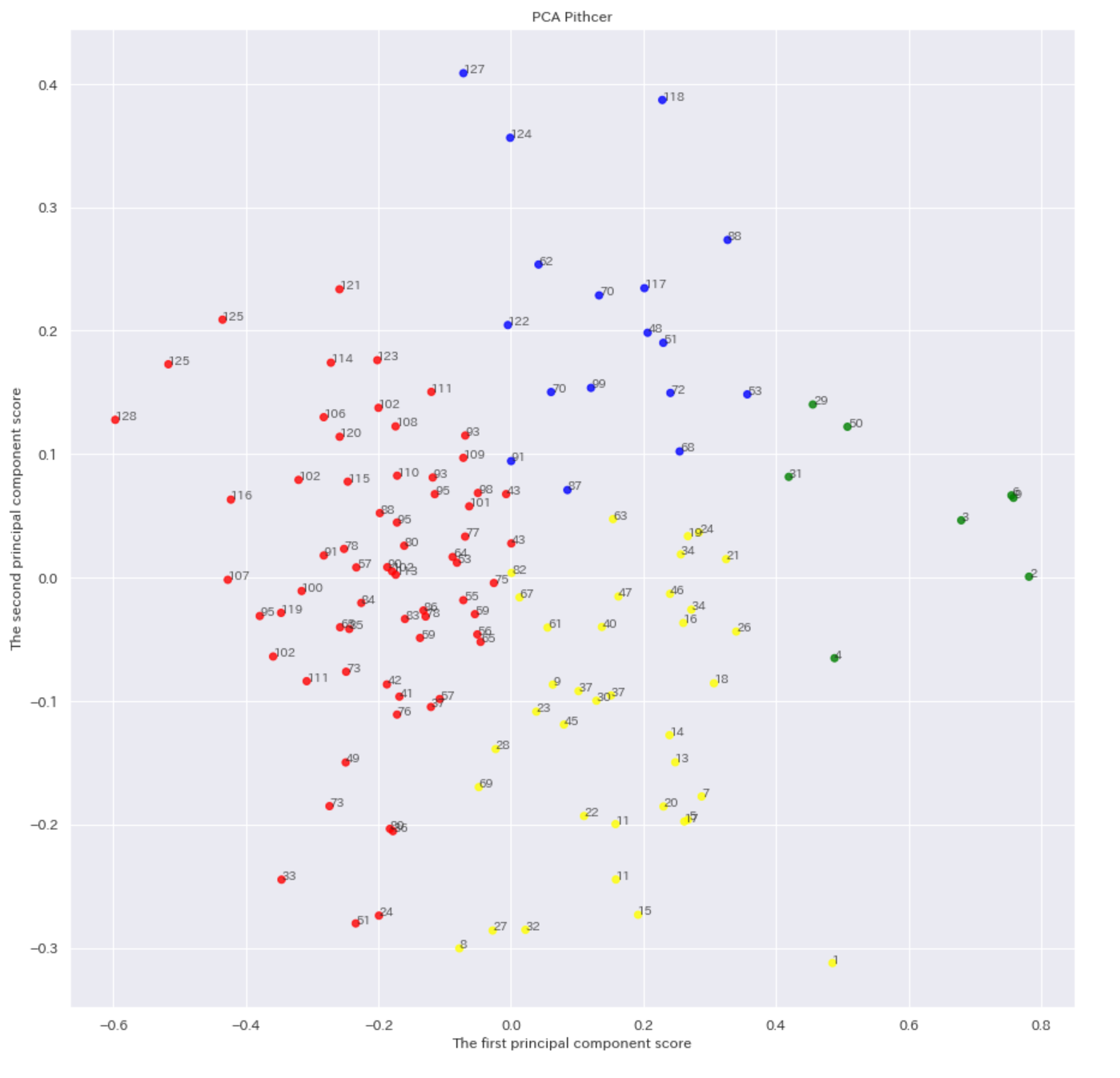
しかしこのグラフではわかりづらいので主成分分析（立体を二次元平面としてとらえてみたイメージ、今回は4次元を2次元にしている）を行ったグラフが下記である。
グラフの点の数字は防御率順位を表している。

グラフ-1 主成分分析後の散布図

各グループの選手の数は
赤(0)：66人
青(1)：17人
黄(2)：37人
緑(3)：8人
となった。

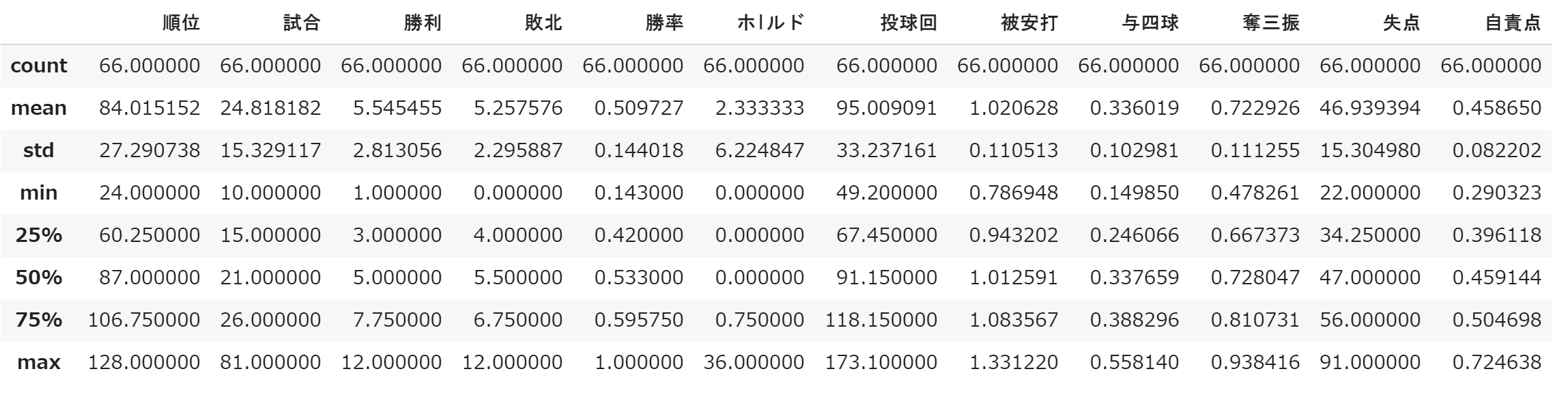
赤グループのピッチャーの成績の基本統計量が下記である。

上の表のホールド数の25%、50%を見てみると0となっていて、多くの選手のホールド数は0であることがわかる。
よって赤グループの多くは先発であることが考えられる。

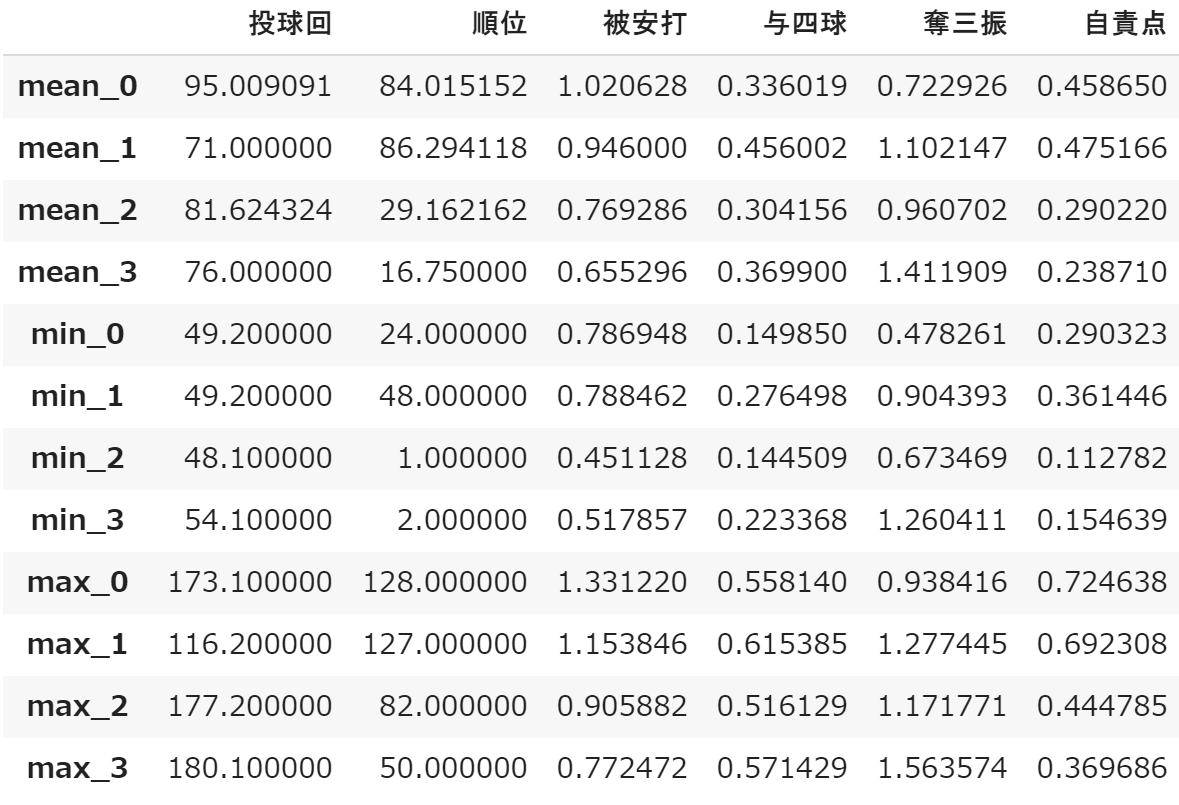
そして各グループの投球回、順位、被安打、与四球、奪三振、自責点の平均値、最小値、最大値をまとめた表が下記のようになった。
mean_0は赤グループの平均値で、そのほかの1,2,3もそれぞれ青、黄、緑と対応している。

上記の表をみてみると奪三振数も多く、平均順位も良く、自責点も少ない緑(3)グループが一番優秀であると考えられる。

グラフ-1を見てみると順位の高い選手（防御率のいい選手）は黄色、緑グループに主に属していることがわかる。
実際に防御率上位10人を調べた表が下記のものだ。
グループが下記の表の一番右に記載されていてる。(2⇒黄色、3⇒緑)

何が黄色と緑を分けているのか上の表を見て考えた。
私は奪三振数がこの２つのグループを分けているのではないかと考えた。
つまり良く耳にする打って守るタイプか、三振を取って守るタイプの違いである。
このように一般的な考え方がデータからも読み取れることがわかり興味深かった。
ちょうど黄色と緑グループが半分ずつ上位10人を占めていることも面白かった。

グラフ-1を見てみると緑グループの上部に50位、29位、31位とほかの緑グループの選手と比べて順位の低い選手がいる。
それらが下記の3選手である。

これらの3選手は防御率の順位の高い人が多い緑グループに属しいるため、さらに良い防御率の可能性を秘めていると考えることができる。

感想

野球に関しての専門知識はそんなになかったが、今回クラスタリングという手法を使うことによって大量のデータからいろいろなパターンが見えてきて面白かった。
同時にデータサイエンスの手法だけでなく分析するためには分野の専門知識も重要であると感じた。
また時間があれば先発中継ぎなどを分けたり、チーム、年齢なども考慮して詳細な分析を行いたいと思う。
機会があればほかのスポーツなども考えてデータサイエンスの可能性を広げていきたいと思う。
データの正規化の必要性、グループの分割数、変数選択などは今回あやふやになってしまったためこれからも勉強していきたい。