姿勢制御のための数理 - 2. 姿勢変化の記述

概要

1. 姿勢の記述 (群)
2. (ｺｺ) 姿勢変化の記述 (多様体)
3. 姿勢制御のためのリー群・リー代数
4. 付録: 回転対称性を持つ剛体の姿勢

第二回は姿勢制御における二つの問題,

• そもそも「姿勢」を数学的にどう記述するか,
• 姿勢が (滑らかに) 変化する時, それを記述する数学的オブジェクトはどう変化するのか,

のうち, 二つ目の姿勢の変化を扱う方法を解説する.

まずは姿勢とその変化がパラメータ付けという操作によって可能になり, その時に全射性を仮定すると便利になることを解説する.
この時, 全射性の便利さとトレードオフになる特異点の問題を挙げ, 多様体を導入することで定義される座標近傍系によってそれが解消されることを見ていく.
さらに多様体によって得られる効果として, 「変化の量」「最短変化」を扱えるようになることを紹介する.

前提知識

とりあえず前回の話を理解できることを前提にしているのでその程度のユークリッド幾何と線型代数の基礎知識が必要になる.
位相空間論とユークリッド空間上の微分積分論もイメージを掴む程度に知っているといい.

解説

変化の記述

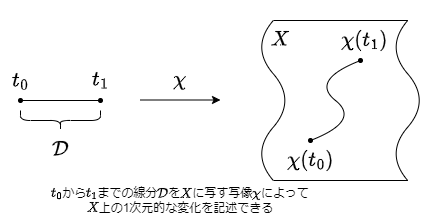
ある集合 $X$ があった時, $X$ の要素の変化を記述するにはユークリッド空間の部分集合 $\mathcal{D} \subset \mathbb{R}^r$ から $X$ への写像を考えるといい.
例えば $r = 1$ として $\mathcal{D} = \{t \in \mathbb{R} \ \vert \ 0 \leq t \leq 1\}$ と取ると, 写像 $\chi: \mathcal{D} \rightarrow X$ によって時間変化のような $1$ 次元的な変化を扱える.
この場合, $\chi(t) \in X$ ($t \in \mathcal{D}$) は時刻 $t$ における $X$ の要素を表していると見なせる.
$r \geq 2$ で $\mathcal{D}$ を取れば, 時間に限らない多次元的な要因による変化を記述できるようになる.

このような $\mathbb{R}^r$ (の部分集合) から $X$ への写像 $\chi$ を $X$ のパラメータ付けと呼び, $\mathcal{D}$ をそのパラメータ集合, $x \in X$ に対して $\chi(t) = x$ となる $t \in \mathcal{D}$ を $x$ のパラメータと呼ぶ.

姿勢変化の記述における問題

前回見たように $d$ 次元の姿勢は特殊ユークリッド群 $SE(d)$ の要素である特殊ユークリッド変換によって記述できるため, パラメータ付け $\chi: \mathcal{D} \rightarrow SE(d)$ によって姿勢の変化を記述することを考える.
ここでは例えば $\chi(0), \chi(1)$ が表す特殊ユークリッド変換は与えられているが $0 \lt t \lt 1$ における $\chi(t)$ は適当に構成する必要がある, というような場合に, $\chi(t)$ が「常に」特殊ユークリッド変換となる $\chi$ をどう構成するかということが問題になる.
特に $\chi(0), \chi(1)$ が複数通り与えられてそれぞれ $\chi$ を決めるといった場合には, $\chi(t) \in SE(d)$ となることが保証される構成法を確立させておきたい.

特殊ユークリッド変換 $\varphi \in SE(d)$ は回転行列 $L_\varphi \in SO(d)$ と平行移動ベクトル $w_\varphi \in \mathbb{R}^d$ によって,

$$ \varphi \sim \varphi^+ := \begin{bmatrix}
L_\varphi & w_\varphi \\
0 & 1 \\
\end{bmatrix} \in M(d+1, \mathbb{R}), $$

と書けることが分かっており, この記述法を用いると $\chi(t)^+ \in M(d+1, \mathbb{R})$ となるよう定めるのは容易だが, $L_{\chi(t)} \in SO(d)$ を保つような構成には工夫が要る.
例えば $\chi$ を連続写像として考えた場合, 上述のように $t_0, t_1 \in \mathcal{D}$ において $\chi(t_0), \chi(t_1)$ が与えられた時に以下のような手法で $\mathcal{D}$ 全体に拡張することがあるが, これらの手法では $L_{\chi(t)} \in SO(d)$ であることが保証されない.

• 補間: $\chi(\lambda t_0+(1-\lambda)t_1) := \lambda\chi(t_0)+(1-\lambda)\chi(t_1)$,
• 差分近似: $\chi(t_2) := \chi(t_1)+\frac{t_2-t_1}{t_1-t_0}(\chi(t_1)-\chi(t_0))$,

全射なパラメータ付けによる姿勢とその変化の記述

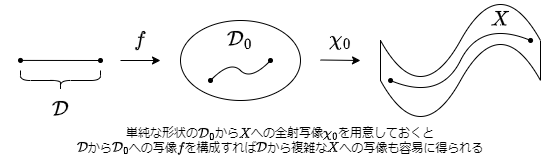
前節の問題を解消するためには, 予め $\mathcal{D}_0 \subset \mathcal{R}^m$ による全射なパラメータ付け $\chi_0: \mathcal{D}_0 \rightarrow SE(d)$ を与えておくといい.
それに対して $\mathcal{D}$ から $\mathcal{D}_0$ への写像 $f: \mathcal{D} \rightarrow \mathcal{D}_0$ との合成によって,

$$ \chi: \mathcal{D} \ni t \mapsto \chi_0\circ f(t) \in SE(d), $$

と構成すると, 比較的容易に姿勢の変化を記述することができるようになる.
このような全射なパラメータ付けは $x \in X$ の変化の記述に用いられるだけでなく, $\mathcal{D}_0$ で生成した乱数を $\chi_0$ に渡してランダムな $X$ の要素に変換する, といった操作にも有用である.

$d = 3$ の場合, $SO(3)$ に関してオイラー角という全射なパラメータ付けの手法が知られており, 意味論との結び付けや実装が容易なためよく用いられている.
オイラー角は座標系の取り方によっていくつか種類があり, 例えば以下で定められるパラメータ付けは全射で, ロール・ピッチ・ヨーと呼ばれるオイラー角の一種を与える.

$$ \begin{gather}
\chi(\theta) := R_0(\theta_0)R_1(\theta_1)R_2(\theta_2), \quad \theta = [\theta_0, \theta_1, \theta_2] \in \mathbb{R}^3, \\
R_0(x) = \begin{bmatrix}
\cos{x} & -\sin{x} & 0 \\
\sin{x} & \cos{x} & 0 \\
0 & 0 & 1 \\
\end{bmatrix}, \\
R_1(x) = \begin{bmatrix}
\cos{x} & 0 & \sin{x} \\
0 & 1 & 0 \\
-\sin{x} & 0 & \cos{x} \\
\end{bmatrix}, \\
R_2(x) = \begin{bmatrix}
1 & 0 & 0 \\
0 & \cos{x} & -\sin{x} \\
0 & \sin{x} & \cos{x} \\
\end{bmatrix}. \\
\end{gather} $$

任意の $x \in \mathbb{R}$ に対して $R_0(x), R_1(x), R_2(x)$ がいずれも $SO(3)$ に属すことに注意すると, $SO(3)$ は行列積について群となることから, $R_0(\theta_0), R_1(\theta_1), R_2(\theta_2)$ の積で定義される $\chi(\theta)$ もまた $SO(3)$ の要素となることが分かる.
$SE(3)$ のパラメータ付けにはこれを用いて,

$$ \tilde{\chi}(\theta, w): \mathbb{R}^3 \ni x \mapsto \chi(\theta)x+w \in \mathbb{R}^3, \quad \theta, w \in \mathbb{R}^3, $$

のように, $\chi(\theta)$ を回転行列部分に持つ特殊ユークリッド変換のパラメータ付けとして $\tilde{\chi}: \mathbb{R}^6 \rightarrow SE(3)$ を定めればいい.

全射なパラメータ付け $\chi: \mathcal{D}_0 \rightarrow X$ は対象集合の要素 $x \in X$ の記述法にもなっている.
回転群におけるロール・ピッチ・ヨーの例では, パラメータ $\theta = [\theta_0, \theta_1, \theta_2]$ を決めることは対応する回転行列 $P = \chi(\theta)$ を取ることに等しく, これは $\theta$ によって $P$ 及び $P$ が示す姿勢を記述していると言い換えることができる.
回転行列による記述と異なり, $\theta, \theta'$ が同じ姿勢を記述するパラメータだとしても $\theta = \theta'$ となるとは限らないことに注意.

ジンバルロックとパラメータの変換による解消

オイラー角によって $SO(3)$ を記述した時, ジンバルロックと呼ばれる問題が起こることが知られている.
これは $SO(3)$ が局所的に $3$ 次元の広がりを持っている (詳細は次節) のに対して, 一方でロール・ピッチ・ヨーによるパラメータ付け $\chi(\theta) = R_0(\theta_0)R_1(\theta_1)R_2(\theta_2)$ では, $\theta_1 = \pm\pi/2$ の時に $2$ 次元的な変化しか表現できないことに起因する.
これは数式により, 偏微分 $\partial\chi/\partial\theta_i(\theta)$ ($i = 0, 1, 2$) で与えられる $3$ つのベクトルが, $\theta_1 = \pm\pi/2$ において $2$ 次元空間を張る¹ ($3$ つとも取ると線型従属になる) と定式化され, このような問題が起こる点をパラメータ付け $\chi$ の特異点と呼ぶ.

この解消法の一つは, ジンバルロックが発生する時 (または発生する点に近づいた時) に, 別のオイラー角 ($\chi'(\theta) := R_1(\theta_0)R_2(\theta_1)R_0(\theta_2)$ 等) に変換して処理を続けることである.
実際, 例えば $\chi(\theta) = R_0(\theta_0)R_1(\theta_1)R_2(\theta_2)$ では $\theta_g = [0, \pi/2, 0]$ が特異点となりジンバルロックが生じるが, $\chi'(\theta) = \chi(\theta_g)$ を解いて得られる $\theta = [\pi/2, 0, 0]$ は $\chi'$ の特異点ではなくなる.

このように, 複数のパラメータ付け $\chi_\lambda: \mathcal{D}_ \lambda \rightarrow X$ ($\lambda \in \Lambda$ は適当な添え字) を考えて, 扱う点 $x \in X$ によって $\chi_\lambda$ を取り換える方法は, 多様体という概念を使って体系化される.

多様体

多様体の定義と性質を見ていく.
端折るところが多いので必要に応じて多様体についての専門書や講義資料等を参照して欲しい.

位相空間 (概論)

ユークリッド空間のように「集合の要素の連続的な変化」が定義された空間²を位相空間と呼び, 多様体は位相空間をベースにして定義される.
ここでは特殊ユークリッド群や回転群が主対象であるため, 「位相空間とはユークリッド空間の部分集合である」と考えていい.

位相空間と位相空間の間には連続写像を定義することができる.
特に位相空間 $X$ から位相空間 $Y$ への写像 $f: X \rightarrow Y$ が連続かつ全単射 (故に逆写像を持つ) で, さらに逆写像 $f^{-1}: Y \rightarrow X$ も連続となる時, $f$ を同相写像と呼び, 同相写像が存在する位相空間 $X, Y$ は同相であると言われる.
また, 位相空間 $X, Y$ の各点にある種の対応付け³がある時, 対応する点それぞれの近傍⁴が同相となる時, $X$ と $Y$ は (対応するそれぞれの点において) 局所同相であると言う.

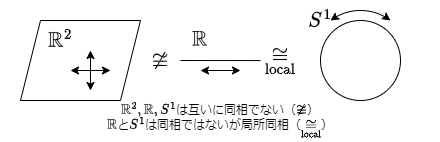
位相空間が同相であるということは, 「双方の空間の要素が (変化量や曲がり方等を無視すれば) 同じように連続変化できる」ということである.
例えば $\mathbb{R}^2$ は各点で平面的な各方向に連続変化可能なのに対して $\mathbb{R}$ は各点で正負どちらかの方向にしか変化できず, これは $\mathbb{R}^2$ と $\mathbb{R}$ が同相ではないことを意味する.
一方で円周 $S^1 := \{x \in \mathbb{R}^2 \ \vert \ \|x\| = 1\}$ を考えると, これはある点から一周して元の点に戻るという連続変化が可能なので一方向に変化し続けても同じ点に戻らない $\mathbb{R}$ と同相ではないが, 各点の近くを見ると時計回りまたは反時計回りの二方向に限定されるので $\mathbb{R}$ と局所同相性がある.

位相空間 (及び次で紹介する多様体) にはハウスドルフ性等の「良い性質」が多く定められ, 以降の議論にもそれらの「良い性質」を必要とするものが多い.
しかし, ここでは簡便のため必要な「良い性質」を適宜持っているものとして特に言及せず議論を進め, 厳密な議論にはそのような「良い性質」を持っているかの仮定まで必要になる, ということは注意に留めておく.

局所座標系

位相空間 $X$ が任意の点 $p \in X$ において, $p$ によらない $m$ 次元ユークリッド空間 $\mathbb{R}^m$ と局所同相な時, $X$ を ($m$ 次元) 多様体と呼ぶ.
砕けた表現では「多様体とは局所的にユークリッド空間だと見なせる集合である」等と言われ, この記事の言葉では任意の点 $p \in X$ の近傍 $U_p \subset X$ において同相なパラメータ付け $\chi_p: \mathcal{D}_p \rightarrow U_p$ ($\mathcal{D}_p \subset \mathbb{R}^m$: 開集合) を定めることができる集合 $X$ が多様体である.
この同相なパラメータ付け $\chi_p$ は, $p \in X$ における局所座標系と呼ばれる⁵.

局所座標系 $\chi_p$ は同相である必要があり, 一般には $X$ の全射なパラメータ付けとしては与えられない.
例えば $SO(d)$ は任意の $d \geq 1$ に対して多様体構造を持つことが知られており, $d = 3$ ではオイラー角の定義域を適当に制限すれば $SO(3)$ の部分集合への局所同相な写像となっている⁶.
前節で定めたロール・ピッチ・ヨーの場合,

$$ -\pi \lt \theta_0 \lt \pi, \quad -\pi/2 \lt \theta_1 \lt \pi/2, \quad -\pi \lt \theta_2 \lt \pi, $$

等, 写像が単射になってかつジンバルロックが起こる $\theta_1 = \pm\pi/2$ が含まれないように定めれば局所同相となる.
$SE(d)$ の場合は, 回転行列部分では $SO(d)$ の多様体構造から定まる局所同相写像を考え, 平行移動ベクトル部分に関する $\mathbb{R}^d$ からの恒等写像と組み合わせれば $SE(d)$ の局所同相写像が得られ, $SE(d)$ もまた多様体となることが分かる.

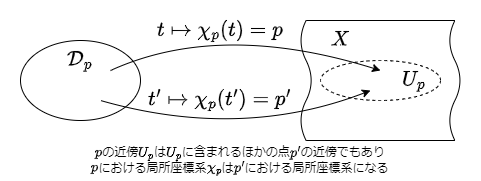
ここで注意したいのは, 局所座標系は各点ごとに異なるものを定める必要はないということである.
実際, ある点 $p \in X$ において局所座標系 $\chi_p: \mathcal{D}_p \rightarrow U_p$ を取った時, $p$ 以外の点 $p' \in U_p\setminus\{p\}$ を取ると $U_p$ は $p'$ の近傍でもあり, $\chi_p$ が $p'$ における局所座標系となることを示している.

特に一般次元の回転群 $SO(d)$ の場合, 有限個の回転行列 $P_0, P_1, \dots, P_{k-1} \in SO(d)$ で, 以下を満たすものが取れることが知られている⁷:

• 各 $P_i$ 近傍 $U_i \subset SO(d)$ がある $\mathcal{D}_i \subset \mathbb{R}^m$ と同相,
• $\bigcup_{i=0}^{k-1}U_i = SO(d)$ が成り立つ ($U_0, U_1, \dots, U_{k-1}$ は開被覆であるという).

これは任意の回転行列 $P \in SO(d)$ がある局所座標系 $\chi _{P_i}: \mathcal{D}_i \rightarrow U_i$ によってパラメータ付けられるということであり, このように多様体 $X$ の任意の点をパラメータ付けできる局所座標系の組 $\{\chi _{p_0}, \chi _{p_1}, \dots, \chi _{p_k}\}$ を $X$ の座標近傍系と呼ぶ.

計量・曲線の長さ

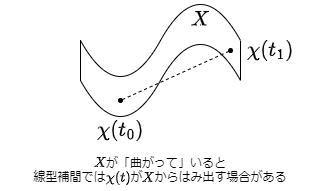
集合 $X$ に多様体の構造を導入する利点の一つに, $1$ 次元の滑らかな (微分可能な) 変化 $\chi: \mathcal{D} \rightarrow X$ ($\mathcal{D} \subset \mathbb{R}$) の変化量 $=$ 曲線の長さを計算できることが挙げられる.

単純に考えるとユークリッド空間との局所同相性を利用して, 局所座標系 $\chi_p: \mathcal{D}_p \rightarrow U_p$ によって, $\mathcal{D}_p \subset \mathbb{R}^m$ 上のユークリッド距離から $U_p$ 上の距離を定めると良さそうだが, 多様体はユークリッド距離に捉われない空間の構成を可能にする概念なので, 一般にユークリッド距離を当てはめようとすると不整合が起こる⁸⁹.

それを解消するため, 多様体には (リーマン) 計量¹⁰と呼ばれる「微小変化量」を表す構造を入れることができる.
多様体について調べると頻出するリーマン多様体とはこのリーマン計量を定めた多様体を指している.
計量を用いると多様体 $X$ 上の曲線 $c: \mathcal{D} \rightarrow X$ ($\mathcal{D} \subset \mathbb{R}$) に対して,

$$ |c| := \int_\mathcal{D}g\left(\frac{dc}{dt}, \frac{dc}{dt}\right)^\frac{1}{2}dt, $$

という積分によって $c$ の長さを計算できる (計量 $g$ や多様体写像の微分 $\frac{dc}{dt}$ の厳密な定義は省く).
これは通常のユークリッド空間上の曲線 $c: \mathcal{D} \rightarrow \mathbb{R}^n$ の長さが,

$$ |c| := \int_\mathcal{D}\left\|\frac{dc}{dt}(t)\right\|dt = \int_\mathcal{D}\left(\sum_{i=0}^{n-1}\left(\frac{dc_i}{dt}(t)\right)^2\right)^\frac{1}{2}dt, $$

によって求められることに対応する.

計量は多様体に対して「定める」必要があることに注意したい.
つまり一般には多様体に対して「自然に定まる計量」というものは存在せず, 曲線の長さは定めた計量によって変わる.
ただし $SO(d)$ や $SE(d)$ には群としての性質も踏まえた自然な計量を定めることができ, 次回紹介する姿勢制御のためのリー群の理論に繋がる.

測地線・指数写像

姿勢を扱う時, しばしば与えられた二姿勢 $\varphi_0, \varphi_1 \in SE(d)$ の間を最短 (かつ等速) で移る変化を記述する必要が出て来る.
このような最短変化を記述する曲線も多様体の理論で扱うことができ, その曲線及びその延長線を測地線と呼ぶ.
注意として, 測地線が与える「最短性」は計量の定め方に依存し, 例えば姿勢変化を $SE(d)$ のリー群としての測地線で記述すると必ずしもユークリッド空間内の直線運動にならない (次回または参考資料の一つ目を参照).
そのような問題は次回取り上げるとして, ここでは測地線に関する一般論を見ていこう.

ここでやはり困るのはそのような測地線をどのように構成すればいいのかという問題である.
特に多様体 $X$ 上で与えられた二点 $p_0, p_1 \in X$ を通る測地線を得る手続きがあると嬉しい.

前半でのパラメータ付けについての話を思い出すと, パラメータ集合 $\mathcal{D}$ から $X$ への写像が多様体上の点の変化を記述するがその具体的な構成が難しいという問題を挙げ, 全射なパラメータ付け $\mathcal{D}_0 \rightarrow X$ を用意しておけば個々のパラメータ付けは $\mathcal{D}$ から $\mathcal{D}_0$ への写像に帰着されるので問題が比較的容易になるという解決策を与えた.
測地線についても, 多様体に対して一つに定まる大域的な写像から局所的な測地線を構成する方法が知られており, この「大域的な写像」が指数写像と呼ばれるものになる.
実数関数としての指数関数とは必ずしも同じものを指さないことに注意しておこう.

指数写像は多様体の接空間から多様体への写像として定義される.
厳密な定義は避けるが, 接空間とは多様体と局所同相なユークリッド空間である, つまり $m$ 次元多様体の接空間は $\mathbb{R}^m$ であると思っておこう.
多様体 $X$ に対して接空間を $T \sim \mathbb{R}^m$, 指数写像を $\exp: T \rightarrow X$ と書くと, $p_0, p_1$ を通る測地線は以下のように構成される:
ある $v \in T$ 及び $t_0, t_1 \in \mathbb{R}$ で,

$$ \exp{(t_0v)} = p_0, \quad \exp{(t_1v)} = p_1, $$

となるものが存在した時, $t_0, t_1$ を含むパラメータ集合 $\mathcal{D} \subset \mathbb{R}$ によって,

$$ c: \mathcal{D} \ni t \mapsto \exp{(tv)} \in X, $$

で $X$ の曲線を定めると, これは $p_0, p_1$ を通る測地線となる.

また, 接空間は各点 $p \in X$ に対応するものが取れて (これを $T_p$ と書く), この時の指数写像を $\exp_p$ と書くと, $\exp_p{(0)} = p$ が成り立つ.
よって, $p_0$ における指数写像 $\exp_{p_0}$ と $p_1$ の「対数」となる $v$, つまり $\exp_{p_0}{(v)} = p_1$ となる $v \in T_{p_0}$ が得られれば, $v$ を探すだけで $p_0$ と $p_1$ を通る測地線を構成できることになる.

ここで終わると指数写像の具体的構成方法が分からない, というたらい回しが発生するので次で扱う予定のリー群上の指数写像に触れておこう.
リー群の接空間はリー代数と呼ばれ, $SE(d), SO(d)$ のような行列の集合として与えられるリー群については, そのリー代数が同じサイズの行列からなるベクトル空間 (の部分空間) として書ける.
この時, 多様体としての指数写像が行列としての指数関数を用いて書けるため, 今回は「指数写像とは行列指数関数である」というイメージで理解しておけばいい.

参考資料

具体的計算を伴う解説はこちらから.

ロボット技術者向け 速習(1) リー群・リー代数を使った3次元回転表現 - Qiita

CV・CG・ロボティクスのためのリー群・リー代数入門: (0) 目次 - swk's log はてな別館

多様体の理論はこちらの講義資料に必要な情報が揃っている.

幾何学特論第四/2011/山田光太郎

1. 多様体の議論を見越した時はこれを「$\chi: \mathbb{R}^3 \rightarrow SO(3)$ が局所同相写像でないため」と説明する場合もあるが, 厳密にはパラメータ集合が $4$ 次元以上の開集合で局所同相になり得ない場合でも, 偏微分で得られるベクトルが常に $3$ 次元空間を張るなら十分である. 実際, パラメータを適当に増やして $\chi^*(\theta^*) := R_0(\theta_0)R_1(\theta_1)R_2(\theta_2)R_0(\theta_3)$ 等と取ると $4$ 次元空間から $3$ 次元多様体への連続写像となり局所同相にはならないがジンバルロックは回避できる (演習). ↩

2. 厳密には「部分集合が開集合となるかどうか」を設定することで「集合の要素の連続的な変化」を扱えるようにした空間である. ↩

3. 通常は「局所同相な写像」は定義されるが「局所同相な空間」は定義されない. にも関わらず多様体の定義には自然に「ユークリッド空間と局所同相な位相空間」という概念が発生するのでその辺りの曖昧さを「ある種の対応付け」という表現に込めた. ↩

4. その点を含む開集合を意味する. ↩

5. 通常, 局所座標系は $\chi_p$ の逆写像を指すが, ほぼ同値なのでここではパラメータ付けとの関連付けのためこの定義を採用した. ↩

6. 回転群としての階数 $d = 3$ と多様体としての次元 $m = 3$ が一致しているのはたまたまである. 一般に回転群 $SO(d)$ の多様体次元は $m = d(d-1)/2$ となる. ↩

7. そのような $P_0, P_1, \dots, P_k \in SO(d)$ の具体的構成は演習. ↩

8. 球面上に全ての角が直角な三角形を描ける, というあれである. ↩

9. より大きな次元のユークリッド距離ならば矛盾なく当てはめられるという話はある (埋め込み定理). ↩

10. 機械学習における計量学習 (metric learning) はこの計量を学習によって求めることを意味する. ↩