はじめに
- 最適輸送は「確率分布の比較」に使えるツール
- 物流や交通整理の話ではない!!
文字面だけみると間違えがちですよね。私もそうでした。
参考資料
最適輸送とは
最適輸送の基本的な考え方は以下の通りです。
ある確率分布に従う質量(あるいは確率)を、別の確率分布に移動させるために必要なコストを最小化するような輸送方法を求める
というものです。
最適輸送に関する質問にお答えします。
最適輸送に関する質問にお答えします。
Q: 最適輸送は何の一種か?
A: 最適輸送は、確率論や解析学における数学的概念の一種です。
Q: 最適輸送は、他とどこが違うのか?
A: 最適輸送は、2つの確率分布の間の距離を定義する方法の一つで、分布間の幾何学的な構造を考慮できる点が特徴です。従来のKLダイバージェンスなどの距離とは異なる性質を持ちます。
Q: 最適輸送とは何か?何をもって最適輸送か?
A: 最適輸送とは、ある確率分布を別の確率分布に変換するための最適な方法を指します。総輸送コストを最小化する輸送写像Tを求めることを最適輸送問題と呼びます。
Q: 最適輸送の要素を1つづつ挙げると?
A: 最適輸送を構成する要素は以下です。
・(1)確率空間X, Y,
・(2)X上の確率分布μ,
・(3)Y上の確率分布ν,
・(4)コスト関数(距離関数)d,
・(5)輸送写像T
Q: 最適輸送の必要条件は何か?
A: 最適輸送が定義されるためには、(1)確率空間X, Yが距離空間であること, (2)μ, νが確率測度であること, (3)コスト関数dが適切に定義されていることが必要です。
Q: 最適輸送の反対は?最適輸送にならない場合は?
A: 最適輸送の反対は「非最適な輸送」と言えます。最適輸送問題を解かない、あるいは最適でない輸送写像を用いる場合は、総輸送コストが最小にならず、確率分布間の距離の性質が失われてしまいます。
Q: 最適輸送を生じさせる(た)ものは?最適輸送のきっかけは?
A: 最適輸送理論は、18世紀のMonge氏による輸送問題の定式化に端を発しています。その後、20世紀半ばにKantorovich氏によって線形計画問題として一般化され、現在の最適輸送理論の基礎が確立されました。
Q: 最適輸送から生じるものは?最適輸送するとどうなる?
A: 最適輸送から、Wasserstein距離を始めとする様々な確率分布間の距離が導出されます。機械学習では、生成モデルの評価、ドメイン適応、確率分布の補間、ロバストな損失関数など、幅広い応用が生まれています。最適輸送を用いることで、確率分布の幾何構造を考慮したアルゴリズムの設計が可能になります。
確率分布の幾何構造を考慮する
確率分布の幾何構造を考慮するとは、確率分布が定義された空間の幾何学的な性質を考慮に入れて、分布間の関係を解析することを指します。
従来、確率分布間の類似度はKLダイバージェンスなどの情報理論的な尺度で測られることが多かったです。しかし、これらの尺度は確率分布が定義された空間の幾何的構造を無視しています。
一方、最適輸送の理論では、確率分布が定義された空間をメトリック空間(距離空間)とみなし、その上で分布間の輸送コストを最小化するような輸送方法を考えます。この輸送コストは、空間の幾何構造(距離関数)に依存します。
例えば、ユークリッド空間上の確率分布を考える場合、輸送コストはユークリッド距離に基づいて定義されます。これにより、分布の幾何学的な位置関係が考慮されます。
また、ワッサーシュタイン空間と呼ばれる、確率分布全体の成す空間を考えることもできます。この空間は、最適輸送コストをメトリックとして持つメトリック空間となります。ワッサーシュタイン空間上では、確率分布間の補間や勾配降下法などの操作が幾何学的に意味を持ちます。
このように、確率分布の幾何構造を考慮することで、より豊かな分布間の関係を捉えることができます。これは特に、機械学習において生成モデルを扱う際などに重要になってきます。確率分布の幾何的性質を考慮したアルゴリズムを設計することで、より良い生成結果が得られることが知られています。
最適輸送と従来手法との比較
以下の表は、最適輸送と従来手法との比較を示しています。
| 観点 | 最適輸送 | 従来手法(KLダイバージェンスなど) |
|---|---|---|
| 基本概念 | 確率分布間の最適な輸送コストを考える | 確率分布間の情報量の差異を測る |
| 幾何構造の考慮 | 確率分布が定義された空間の幾何構造を考慮 | 確率分布の幾何構造は考慮しない |
| 距離の性質 | 三角不等式を満たすメトリックとなる | メトリックとはならない場合がある |
| 計算量 | 一般に高い計算量を要する | 比較的計算量が少ない |
| 勾配計算 | 勾配を計算できる(Wasserstein GANなど) | 勾配の計算が困難な場合がある |
| 確率分布の補間 | 最適輸送に基づく自然な補間が定義できる | 補間の定義が自明ではない |
| 確率分布の生成 | 生成モデルの学習に利用できる | 生成モデルへの応用は限定的 |
| 異常検知 | 確率分布の幾何構造を考慮した異常検知が可能 | 確率分布の形状の変化を捉えにくい |
| 適用可能な問題 | 画像生成、ドメイン適応、形状解析など | 分類、クラスタリングなど |
| 理論的保証 | 輸送不等式などの理論的保証がある | 情報幾何の理論に基づく |
最適輸送は、確率分布の幾何構造を考慮できる点や、メトリック空間の構造を持つ点などが特徴です。また、生成モデルや異常検知など、機械学習の新しい応用領域で注目されています。一方で、計算量が高いことがしばしば問題となります。
従来手法は、情報理論に基づく尺度が中心で、計算量は比較的少ないですが、確率分布の幾何的性質を捉えにくいという問題があります。
最適輸送 のライブラリ
| ライブラリ | 説明 |
|---|---|
| POT (Python Optimal Transport) | - 最も広く使われている最適輸送のPythonライブラリ - 離散・半離散・連続な最適輸送問題を扱うことができる - Wasserstein距離、Sinkhorn divergence、Gromov-Wasserstein距離などを計算できる |
| Ot (Optimal transport tools) | - 最適輸送問題を解くためのシンプルなPythonライブラリ - 線形計画問題としての定式化に基づいている |
| Geomloss | - PyTorchベースの最適輸送ライブラリ - Sinkhorn divergenceを用いた損失関数を提供 - 機械学習モデルの学習に直接利用できる |
| Geomstats | - リーマン多様体上の計算を行うためのPythonライブラリ - ワッサーシュタイン空間など、最適輸送に関連する幾何構造を扱える |
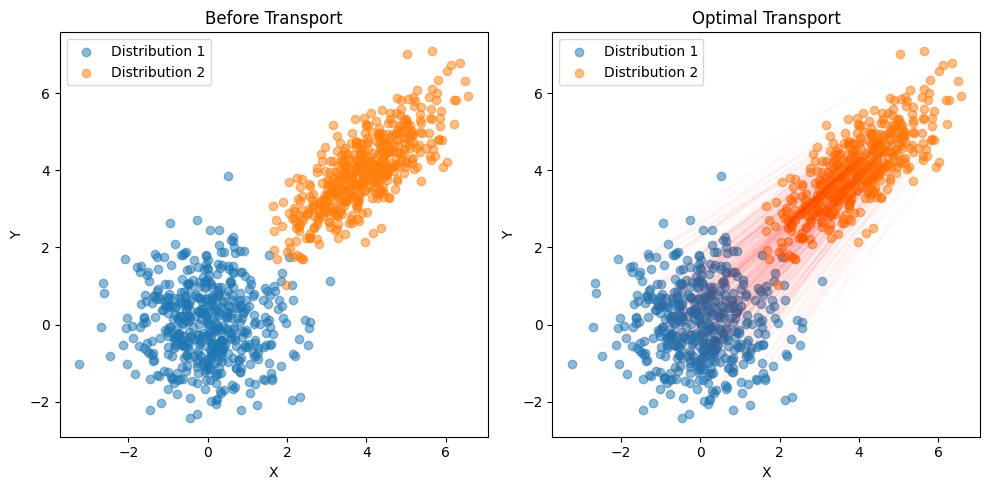
POTを用いた実装例
import numpy as np
import matplotlib.pyplot as plt
import ot
# 2つの2次元ガウス分布を生成
np.random.seed(42)
n = 500 # サンプル数
mean1 = np.array([0, 0])
cov1 = np.array([[1, 0], [0, 1]])
X1 = np.random.multivariate_normal(mean1, cov1, n)
mean2 = np.array([4, 4])
cov2 = np.array([[1, 0.8], [0.8, 1]])
X2 = np.random.multivariate_normal(mean2, cov2, n)
# 確率分布間の最適輸送を計算
M = ot.dist(X1, X2) # 輸送コスト行列を計算
a, b = np.ones((n,)) / n, np.ones((n,)) / n
T = ot.emd(a, b, M) # 最適輸送を計算
# 結果をプロット
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].scatter(X1[:, 0], X1[:, 1], alpha=0.5, label='Distribution 1')
ax[0].scatter(X2[:, 0], X2[:, 1], alpha=0.5, label='Distribution 2')
ax[0].set_title('Before Transport')
ax[0].set_xlabel('X')
ax[0].set_ylabel('Y')
ax[0].legend()
for i in range(n):
for j in range(n):
if T[i, j] > 1e-5:
ax[1].plot([X1[i, 0], X2[j, 0]], [X1[i, 1], X2[j, 1]], 'r-', alpha=T[i, j]*10)
ax[1].scatter(X1[:, 0], X1[:, 1], alpha=0.5, label='Distribution 1')
ax[1].scatter(X2[:, 0], X2[:, 1], alpha=0.5, label='Distribution 2')
ax[1].set_title('Optimal Transport')
ax[1].set_xlabel('X')
ax[1].set_ylabel('Y')
ax[1].legend()
plt.tight_layout()
plt.show()