概要
ゲームを作る上で、Transformの変換が必要になる場面がある。
特に回転の計算は、Rotationで計算してもおかしなことになることが多いので、Transformを使うことが多い。
Transformの計算は公式さえ覚えていれば基本的には問題無いが、使用頻度が高くなく忘れがちだったので、備忘録として書き残す。
今回は例として、アクターAから見たアクターBの相対Transformを求めていく。
ワールドの原点はWと記述する。
公式
先に公式を乗せておく
ここでは、Aから見たBの相対Transformを以下のように記述する。
^{A}\boldsymbol{T}_{B}
Transformの変換では、以下の2つの式が成り立つ。
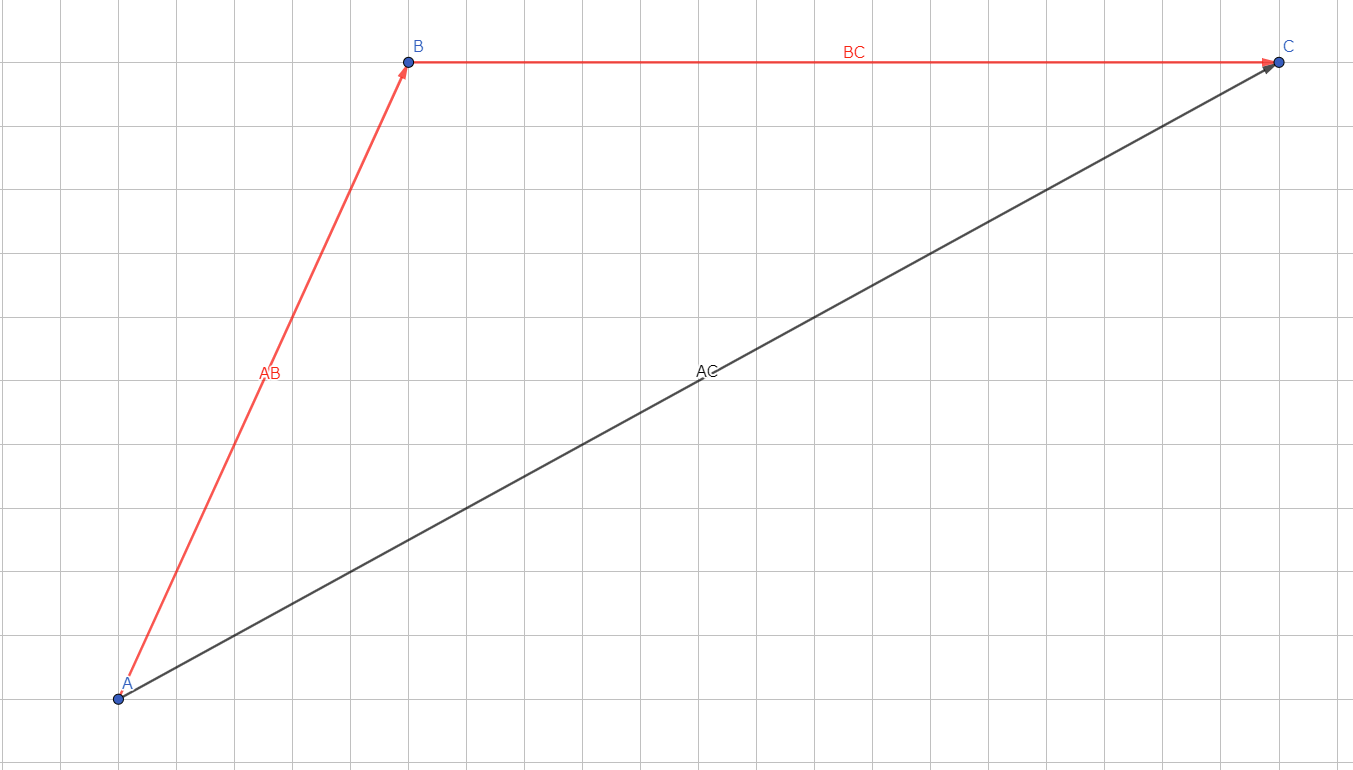
^{A}\boldsymbol{T}_{C}= \, ^{A}\boldsymbol{T}_{B} \, \times \, ^{B}\boldsymbol{T}_{C}
説明:Aから見たCのTransformは、任意の点Bを用いて、AB×BCで求めることも出来る。
(図はベクトルなので、あくまでイメージです)
^{A}\boldsymbol{T}_{B} = (^{B}\boldsymbol{T}_{A})^{-1}
説明:Aから見たBのTransformは、Bから見たAのTransformを反転したものと等しい。
解説
実際に上記公式を使い、Aから見たBの相対Transformを求めていく。
まず、A,BのTransformは、ワールドの原点から見たTransformなので、以下のように記述出来る。
^{W}\boldsymbol{T}_{A}\\
^{W}\boldsymbol{T}_{B}\\
1つ目の公式を用いると、Aから見たBのTransformはワールドの原点Wを用い、以下のように表すことが出来る。
^{A}\boldsymbol{T}_{B}= \, ^{A}\boldsymbol{T}_{W} \, \times \, ^{W}\boldsymbol{T}_{B}
更に2つ目の公式を用いると、Aから見たWのTransformを、Wから見たAのTransformで置き換えることが出来る。
^{A}\boldsymbol{T}_{B}= \, (^{W}\boldsymbol{T}_{A})^{-1} \, \times \, ^{W}\boldsymbol{T}_{B}
結果として、Aから見たBのTransformは、原点から見たAのTransformを反転したもの×原点から見たBのTransformで求めることが出来ることが分かった。
Blueprintでの実装
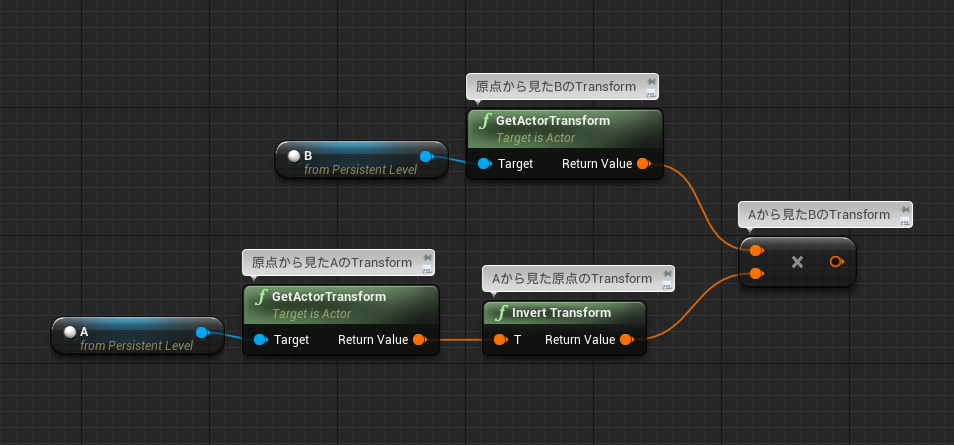
UE4でTransformの計算をする上で一番気を付けなければならないのが、掛け算の順序が逆になっていることである。
先程求めた式の掛け算の順序だけ逆にすれば、Aから見たBのTransformが求められる。
おまけ
Qiitaでは、Transformは以下のように記述することで書くことが出来た。
```math
^{A}\boldsymbol{T}_{B}
```math
^{A}\boldsymbol{T}_{B}