ノッチフィルタについて
本記事ではノッチフィルタについて紹介します.
現場でよく用いられる基本的なフィルタですが, 記事が意外と見当たらない事もあって書いてみようと思います.
ノッチフィルタは以下の図のように, 特定の周波数のゲインが非常に小さくなっているフィルタです. これを制御対象の共振ピークに対して適用する事で, 制御対象の振動を抑制する事ができます.
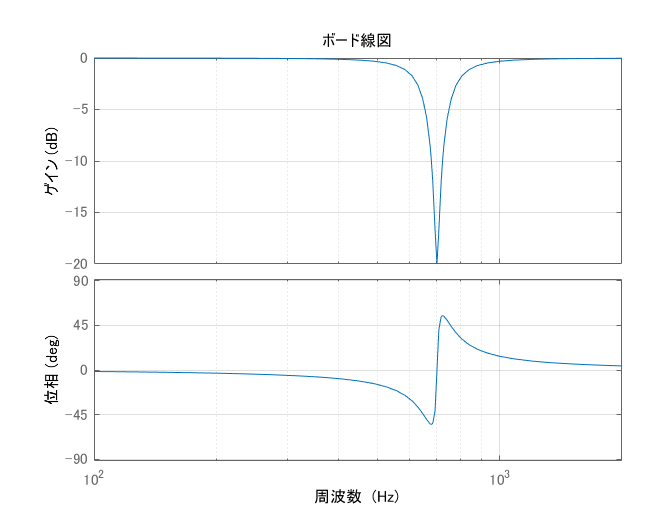
図:ノッチフィルタのボード線図
フィードバック制御のブロック線図で考えると, 以下の位置に入れる事が多いと思います.
本記事は以下の書籍を参考にしましたが、私の拙い知識で書いておりますので誤り等ありましたらご指摘ください.
現場で役立つ制御工学の基本
ナノスケールサーボ制御―高速・高精度に位置を決める技術
精密位置決め・送り系設計のための制御工学
また本記事内のグラフの作成は, MATLABで行っています.
目次
-ノッチフィルタについて
-連続系での表現
-離散化
-実用上のコツ
-その他のノッチフィルタ
-まとめ
連続系での表現
まずノッチフィルタを連続系で表現します. 次数は2次が一般的で, 次数を上げる時には2次ノッチフィルタを多段直列接続して使用します. 2次ノッチフィルタの伝達関数は以下になります.
$$G(s) = \frac{s^2+d\cdot2\zeta\omega_ns+\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2} $$
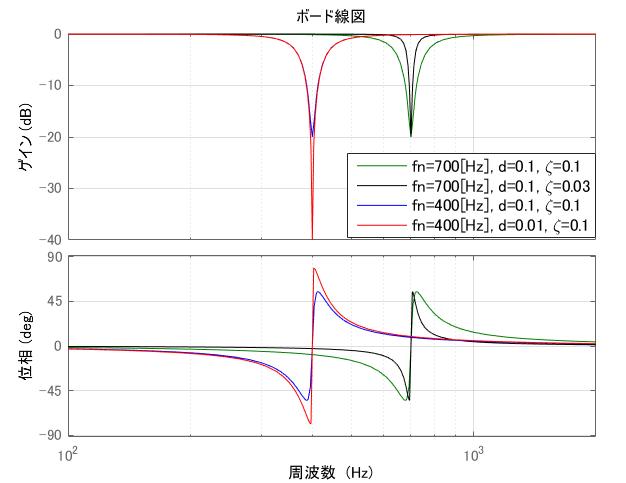
$\omega_n$はノッチの中心周波数$[rad/s]$, $\zeta$はノッチの幅, $d$はノッチの深さを決めるパラメータです.
以下の図のイメージです. なお$w_n = 2\pi f_n$です.
$d$ですが, ノッチの中心周波数における減衰量を表しています. 例えば, $d=0.1$であれば中心周波数での減衰量が$-20[dB]$となり, $d=0.01$であれば減衰量が$-40[dB]$となります. なお, $d>1.0$だと増幅するフィルタとなります.
この事は伝達関数からも簡単に確認できます. 周波数伝達関数$G(j\omega)$の$\omega$に$\omega_n$を代入すると,
$$G(j\omega) = \frac{-\omega^2+d\cdot2\zeta\omega_nj\omega+\omega_n^2}{-\omega^2+2\zeta\omega_nj\omega+\omega_n^2} $$
から
$$G(j\omega_n) = \frac{-\omega_n^2+d\cdot2\zeta\omega_nj\omega_n+\omega_n^2}{-\omega_n^2+2\zeta\omega_nj\omega_n+\omega_n^2}=d$$
となり, 中心周波数$\omega_n$でのゲインが$d$となる事がわかります.
離散化
ここではプリワーピングと双一次変換を用いて, 連続系伝達関数を離散系伝達関数に変換します. 双一次変換については, こちらやこちらに良い記事があります.
ざっくり要約すると, 双一次変換では伝達関数$G(s)$の$s$に対して, 以下の近似式を適用してzの関数$G(z)$として表現します. $T$はサンプリング周期です.
$$s = \frac{2}{T}\cdot\frac{1-z^{-1}}{1+z^{-1}} $$
こうして求めた離散伝達関数$G(z)$を以下のように書き直すと, フィルタ出力を過去のフィルタ出力, 現在&過去のフィルタ入力の線形和で表すことができます. これでソフトウェアに実装できる形になります(サンプル周期毎に以下の数式を計算する事でフィルタとなります).
$$ G(z) = \frac{y[k]}{x[k]}
= \frac{\left\{(1-(\frac{T\omega_n}{2})d2\zeta+(\frac{T\omega_n}{2})^2\right\}z^{-2}+
\left\{2(\frac{T\omega_n}{2})^2-2\right\}z^{-1}+
\left\{1+(\frac{T\omega_n}{2})d2\zeta+(\frac{T\omega_n}{2})^2\right\}}
{\left\{(1-(\frac{T\omega_n}{2})2\zeta+(\frac{T\omega_n}{2})^2\right\}z^{-2}+
\left\{2(\frac{T\omega_n}{2})^2-2\right\}z^{-1}+
\left\{1+(\frac{T\omega_n}{2})2\zeta+(\frac{T\omega_n}{2})^2\right\}} =\frac{N_2z^{-2}+N_1z^{-1}+N_0}{D_2z^{-2}+D_1z^{-1}+D_0}$$
ここで
$$ N_2 = 1-(\frac{T\omega_n}{2})d2\zeta+(\frac{T\omega_n}{2})^2,
\quad N_1 = 2(\frac{T\omega_n}{2})^2-2,
\quad N_0 = 1+(\frac{T\omega_n}{2})d2\zeta+(\frac{T\omega_n}{2})^2$$
$$ D_2 = 1-(\frac{T\omega_n}{2})2\zeta+(\frac{T\omega_n}{2})^2,
\quad D_1 = 2(\frac{T\omega_n}{2})^2-2,
\quad D_0 = 1+(\frac{T\omega_n}{2})2\zeta+(\frac{T\omega_n}{2})^2$$
と置いています. 上式より,
$$ N_2\cdot x[k]z^{-2}+
N_1\cdot x[k]z^{-1}+
N_0\cdot x[k] =
D_2\cdot y[k]z^{-2}+
D_1\cdot y[k]z^{-1}+
D_0\cdot y[k]
$$
を$y[k]$について解いて, $x[k]z^{-1} = x[k-1]$のように書き直すと,
$$ y[k] = \frac{1}{D_0}(N_2\cdot x[k-2]+N_1\cdot x[k-1]+N_0\cdot x[k] - D2\cdot y[k-2]+D1\cdot y[k-1])$$
となります. ここで$x[k]$はノッチへの現時刻の入力, $y[k]$はノッチフィルタの出力, $x[k-1]$は1サンプル前の入力, $y[k-1]$は1サンプル前の出力, $x[k-2]$は2サンプル前の入力, $y[k-2]$は2サンプル前の出力です.
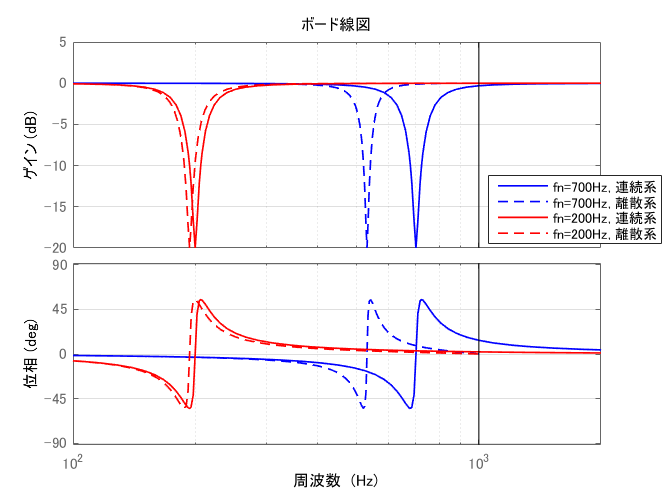
この状態でも一応フィルタとして機能しますが, サンプリング周波数に近づくほど離散化後のフィルタ特性が離散化前の連続系フィルタ特性から乖離していきます. 以下の図は, 2kHzサンプリング時のノッチフィルタ特性比較です. 黒い縦線は2kHzサンプリング時のナイキスト周波数1kHzを表しています. ノッチフィルタは特定の周波数をピンポイントで落としたいので, 中心周波数がずれてしまうと上手く機能させられません.
そこでプリワーピングという処理を用います. これは, あらかじめ中心周波数がずれる事が分かっているので, 離散化前にその分を見越して中心周波数を補正しておくという処理です. 具体的には, 以下の式で中心周波数を変換します.
$$ \omega_n' = \frac{2}{T}\cdot tan(\omega_n\frac{T}{2})$$
先ほど求めた離散伝達関数の係数$N_2$~$D_0$で$\omega_n$の代わりに, この$\omega_n'$を使用すれば連続系のノッチフィルタと同じ中心周波数を持つ離散系のフィルタを作ることができます.
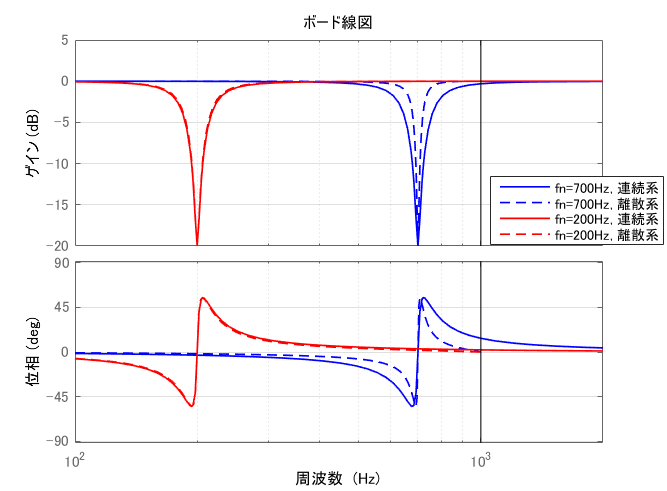
ただし, プリワーピングは中心周波数においての連続系と離散系のずれを無くすだけなので, 以下の図のように離散化後の方がノッチフィルタの幅は小さくなってしまいます. そのため, 幅も連続系に近づけるには, $\zeta$の値も調整する必要があります(こちらは手動での調整です).
実用上のコツ
いくつか実際に適用する上でのポイントがあるので, それを記載します.
(1) 安定性の確認
ノッチフィルタは主に中心周波数付近に大きな影響を与えるフィルタではありますが, それ以外への周波数への影響も無視できない場合があります(低周波側の位相遅れの影響で安定性を損なう可能性があります). ノッチフィルタ適用により, 安定性が損なわれないかの確認は毎回行った方が良いです. これにはボード線図やナイキスト線図を用います. 安定性に関しては, こちらに説明があります.
(2) ノッチによる位相遅れの影響を減らすために
ノッチフィルタの中心周波数以外への影響を極力減らすためには, 可能な限り細いノッチフィルタで共振ピークを落とす必要があります. 複数の共振周波数が近い周波数帯に存在する場合に, 1つの太いノッチフィルタを適用するよりも, 複数の細いノッチフィルタを適用した方が低域の位相遅れを小さくすることができます.
(3) 適用する周波数
ノッチフィルタは中心周波数より低周波側で位相遅れ, 高周波側で位相進み特性となっています. そのため, 共振ピークに対して中心周波数をぴったり合わせると, 位相遅れ部の影響で安定性がなくなる場合があります. そのため, 共振ピークよりも少し低い周波数にノッチ中心周波数を設定し, 位相進み部分が共振ピークに当たるようにするとより安定となるそうです(参照:現場で役立つ制御工学の基本).
※個人的にはあまり意識していませんでしたが, このように設定した方が安全そうです
その他のノッチフィルタ
今回は連続系の2次ノッチフィルタをベースに, 離散化してIIR型のノッチフィルタを求めました. この他にもコムフィルタや移動平均フィルタのように特定周波数を減衰させるものがあります. また適応的にパラメータを変更する適応ノッチフィルタもあるようです.
まとめ
以上がノッチフィルタの基礎でした.
基本的な内容ですが、知っておいて損はないと思います!