ディジタルフィルタと言ってもいろいろありますが、今回はローパスなディジタルフィルタを作成して実際にローがパスされているかを確認します。
ラプラス変換
関数$x(t)$のラプラス変換は次のように定義されます。
X(s) = \mathcal{L} [x(t)] = \int_0^\infty x(t) e^{-s t } dt
$x(t) = 0 \ (t<0)$として$s = i \omega$と置けば$x(t)$をフーリエ変換したものと一致します。
ラプラス変換と畳み込み
$\mathcal{L}[x(t)]=X(s), \ \mathcal{L}[g(t)]=G(s)$と置くと次が得られます。
G(s)X(s)
= \mathcal{L} \bigg[ \int_0^\infty g(\tau)x(t-\tau) d\tau \bigg]
何が嬉しいかと言うと、$s=i\omega$と置けば、周波数領域での積が時間領域での畳み込みになるところです。
z変換
数列$\{x_n\}_{n=0,1,2, \ldots}$の$z$変換は次のように定義されます。ラプラス変換の離散化版のようなものです。
X(z) =
\mathcal{Z}[x_n] =
\sum_{n=0}^\infty x_n z^{-n}
z変換と差分方程式
ラプラス変換で説明した畳み込みの離散化版を導入して、次のような差分方程式を考えます。
y_n = \sum_{k=0}^n b_k x_{n-k} + \sum_{k=1}^n a_k y_{n-k}
両辺に$z^{-k}$を掛けて$k=0$から$\infty$までの総和をとります。$k<0$のときに$y_k=x_k=0$とすれば次が得られます。
Y(z) = H(z) X(z)
ここで$X(z),Y(z),H(z)$は次のようになります。
X(z) = \sum_{n=0}^\infty x_n z^{-n}, \ \
Y(z) = \sum_{n=0}^\infty y_n z^{-n}, \ \
H(z) = \frac{\sum_{k=0}^n b_k z^{-k}}{1 - \sum_{k=1}^n a_k z^{-k}}
何が嬉しいかというと、$H(z)$から逆に差分方程式を求めることが出来るところです。
ラプラス変換からz変換へ
離散信号のラプラス変換
$T$をサンプリング間隔とする
g^{\star}(t) = g(t) \cdot \sum_{n=0}^{\infty} \delta(t-nT)
これをラプラス変換すると以下が得られる。
G^{\star}(s) = \mathcal{L} [g^{\star}(t)] = \sum_{n=0}^{\infty} g(nT) e^{-nTs}
また、留数定理を駆使すると以下が得られる。
G^{\star}(s) = \mathcal{L} [g^{\star}(t)] = \frac{1}{T} \sum_{m=-\infty}^{\infty} G \big( s + im \frac{2\pi}{T} \big)
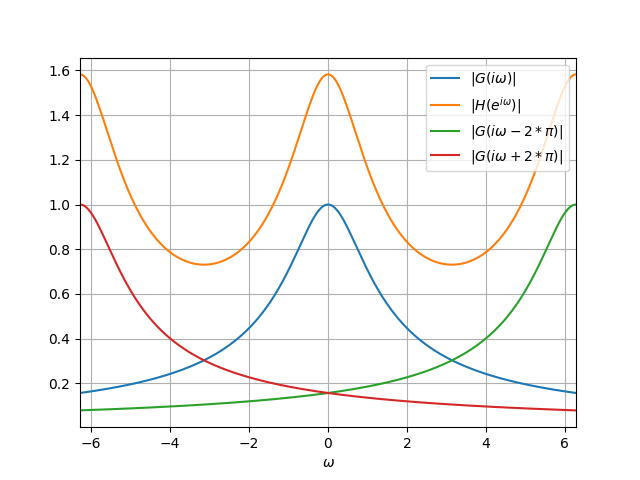
これは$TG^{\star}(s)$が$G(s)$を重ね合わせで表現されることを示している。
アナログフィルタ
ディジタルフィルタの元となるアナログフィルタの例としてバターワースフィルタについて説明します。
バターワースフィルタ
1次のバターワースフィルターは次のように定義されます。
G(s) = \frac{1}{1 + s/ \omega_c}
周波数応答と振幅特性
周波数応答と振幅特性は次のようになります。
G(i \omega) = \frac{1}{1 + i \omega / \omega_c}, \
|G(i \omega)| = \frac{1}{\sqrt{ 1 + (\omega / \omega_c)^2 }}
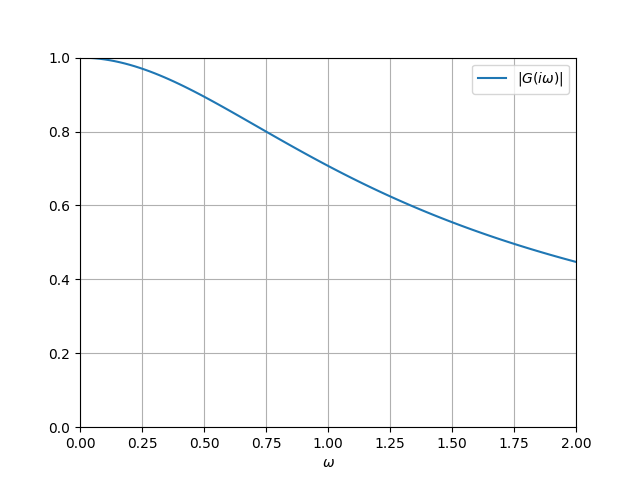
$\omega_c = 1$として振幅特性をグラムに表示してみます。
高次のものと比べると切れが悪いですね。$s = i \omega_c$のときに$|G(i \omega_c)| = 1 / \sqrt{2}$となりますが$\omega_c$のことをカットオフ周波数と言います。
インパルス応答
インパルス応答は次のようになります。
g(t) = \mathcal{L}^{-1} \left[ \frac{1}{1 + s/ \omega_c} \right]
= \omega_c e^{-\omega_c t}
ディジタルフィルタの設計
アナログフィルタを変換してディジタルフィルタを設計するための2つの方法について説明します。
標準z変換
$TG^{\star}(s)$の計算で$e^{sT}=z, g(t) = \omega_c e^{-\omega_c t}$と置いたものを$H(z)$とします。
TG^{\star}(s) = T \sum_{n=0}^\infty g(nT) e^{-nTs} =
T \sum_{n=0}^\infty \omega_c e^{-\omega_c nT} z^{-n} =
\frac{\omega_c T }{1 - e^{-\omega_c T}z^{-1} } = H(z)
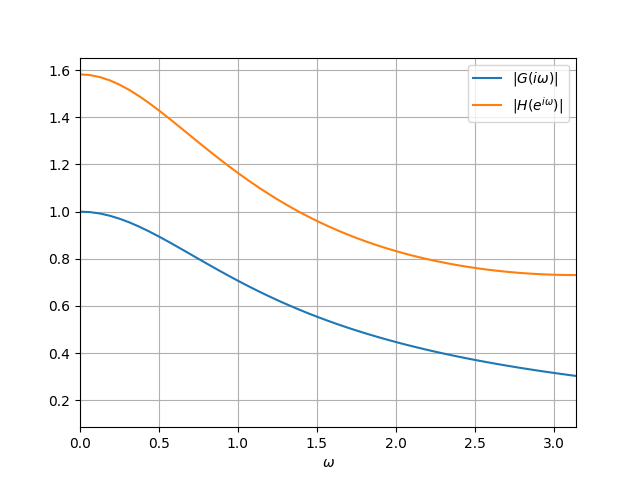
$T=1, \omega_c =1$と置いたときのディジタルフィルタの周波数応答$H(e^{i \omega})$は以下のようになります。
$TG^{\star}(s)$が$G(s)$の重ね合わせになるため折返し歪が発生します。更に今回、フィルタのキレが悪いためその影響を強く受けていることがわかります。折り返し歪の様子を以下にしめします。
このような$z=e^{sT}$に基づく変換を標準z変換(インパルス不変変換)と言います。$H(z)$から次の差分方程式が得られます。
\begin{eqnarray}
b_0 &=& \omega_c T \\
a_1 &=& e^{-\omega_c T} \\
y_k &=& b_0x_k + a_1y_{k-1} \\
\end{eqnarray}
標準z変換は折返し歪が発生するためハイパスフィルタやバンドパスフィルタには適しません。
双一次変換
次のような変換で
s = \frac{2}{T}\tanh(pT/2)
虚数軸を$-\pi/T$から$\pi/T$に移してから標準z変換 $z=e^{pT}$ を行うことにより
s = \frac{2}{T}\tanh(pT/2) = \frac{2}{T} \frac{ 1-e^{-pT} }{ 1+e^{-pT} } = \frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}
が得られます。
双一次変換の利点はアナログフィルタのインパルス応答$g(t)$を経由せずに直接$G(s)$に代入することでディジタルフィルタに変換出来るところですが、カットオフ周波数がズレるので補正を行う必要があります。アナログフィルタの周波数をとディジタルフィルタの周波数をそれぞれ$\omega_a, \omega_d$として双一次変換の式に$s=i \omega_a, \ z=e^{i \omega_d T}$を代入すると次の関係が得られます。
\omega_a = \frac{2}{T} \tan(\omega_d T/2)
この関係式を用いてカットオフ周波数等を予め補正しておくことをプリワーピングと言います。実際に双一次変換を行うと次が得られます。
H(z)
= \frac{1}{1 + \left( \frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} \right) / \left( \frac{2}{T} \tan(\omega_c T /2) \right) }
= \frac{ \tan(\omega_c T /2)/ ( 1 + \tan(\omega_c T /2) ) (1+z^{-1}) }
{1 - ( 1 - \tan(\omega_c T /2) ) / ( 1 + \tan(\omega_c T /2) ) z^{-1} }
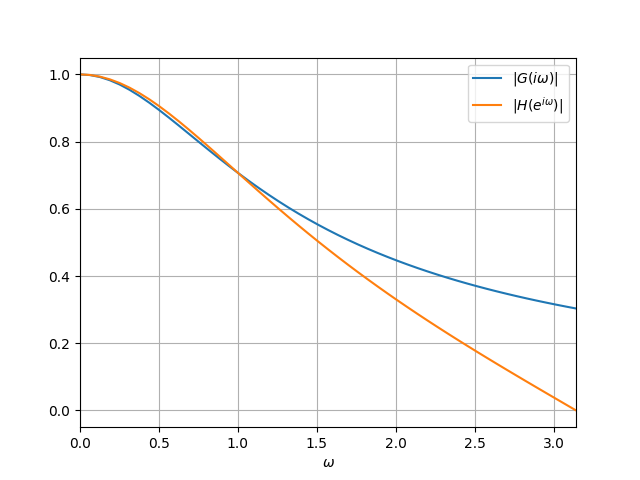
$H(e^{i \omega})$はディジタルフィルタの周波数応答になります。バターワースフィルタの周波数応答$G(i \omega)$と比較してみます。
プリワーピングが効いていますね。$H(z)$から次の差分方程式が得られます。
\begin{eqnarray}
b_0 &=& b_1 = \frac{\tan(\omega_c T /2)}{ 1 + \tan(\omega_c T /2)} \\
a_1 &=& \frac{1 - \tan(\omega_c T /2)}{1 + \tan(\omega_c T /2)} \\
y_k &=& b_0x_k + b_1x_{k-1} + a_1y_{k-1} \\
\end{eqnarray}
実験
Audacityで作成した白色雑音を入力し、出力結果のスペクトルを確認します。-6dBで振幅が半分なのでカットオフ周波数付近で-3dBとなっていればOKとします。
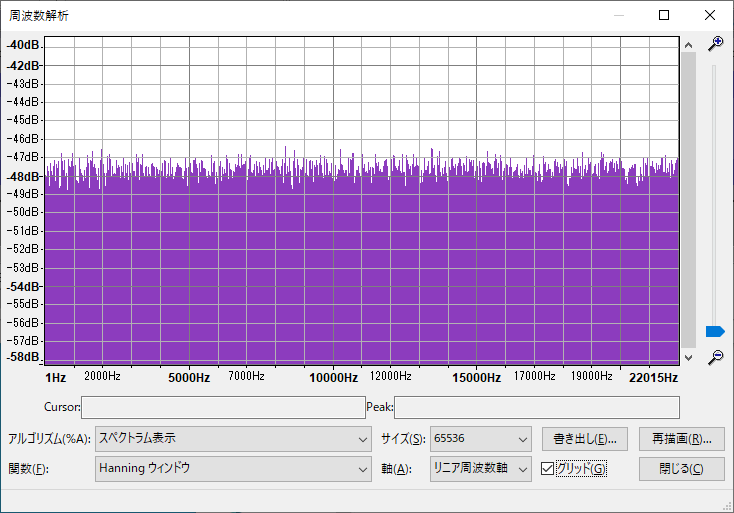
入力
カットオフ周波数は5000Hzに設定して試します。WAVファイルの読み書きはscipyを使用しています。
標準Z変換
ソースコード
import scipy.io.wavfile
import numpy as np
def main():
cutoff = 5000.0
# read
samplerate, read_frames = scipy.io.wavfile.read('in.wav')
assert(read_frames.ndim == 1)
T = 1.0/samplerate
omega_c = 2.0*np.pi*cutoff
b0 = omega_c*T
a1 = np.exp(-omega_c*T)
# filter
y1 = 0.0
write_frames = []
for x0 in read_frames:
y0 = b0*x0 + a1*y1
write_frames.append(y0)
y1 = y0
# write
scipy.io.wavfile.write(
'standard_z_transform.wav',
samplerate,
np.clip(write_frames,-2**15, 2**15-1).astype('int16'))
if __name__ == '__main__':
main()
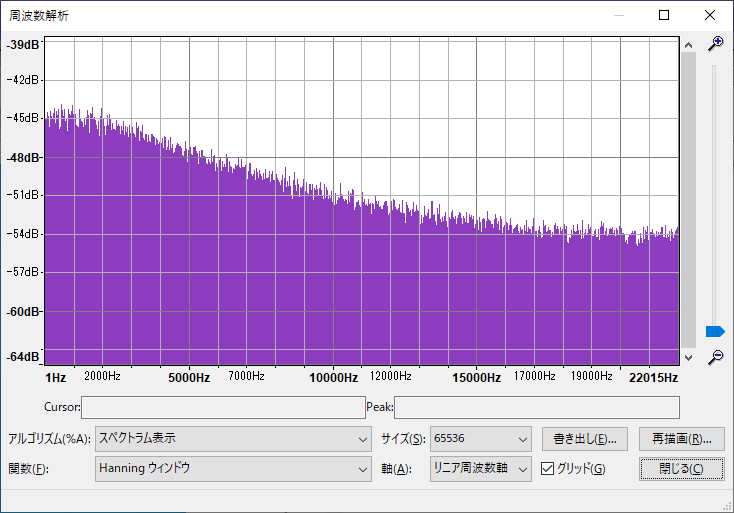
出力結果
5000Hz付近で-3dBになっているように見えます。
双一次変換
ソースコード
import scipy.io.wavfile
import numpy as np
def main():
cutoff = 5000.0
# read
samplerate, read_frames = scipy.io.wavfile.read('in.wav')
assert(read_frames.ndim == 1)
T = 1.0/samplerate
omega_c = 2.0*np.pi*cutoff
b0 = np.tan(omega_c*T/2.0)/(1.0+np.tan(omega_c*T/2.0))
b1 = np.tan(omega_c*T/2.0)/(1.0+np.tan(omega_c*T/2.0))
a1 = (1.0-np.tan(omega_c*T/2.0))/(1.0+np.tan(omega_c*T/2.0))
# filter
x1, y1 = 0.0, 0.0
write_frames = []
for x0 in read_frames:
y0 = b0*x0 + b1*x1 + a1*y1
write_frames.append(y0)
x1, y1 = x0, y0
# write
scipy.io.wavfile.write(
'biliner_transform.wav',
samplerate,
np.clip(write_frames,-2**15, 2**15-1).astype('int16'))
if __name__ == '__main__':
main()
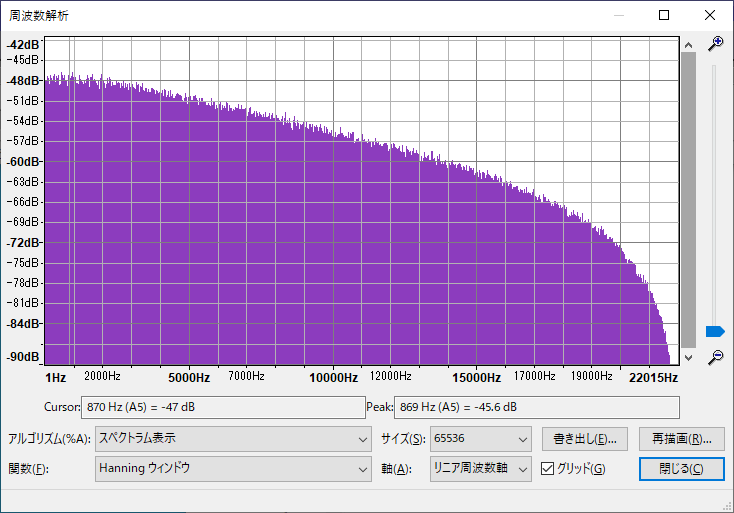
出力結果
5000Hz付近で-3dBになっているように見えます。
リンク
参考文献
- 谷萩隆嗣、ディジタル信号処理と基礎理論(コロナ社)
- 谷萩隆嗣、ディジタルフィルタと信号処理(コロナ社)