0. はじめに
機械学習を使って自動車の運転を制御し、自動運転を想定したシミュレーションができないかと考え、やってみました。
ソースコード(Google Colaboratoryへのリンク)
モデルに関する詳しい議論を除けば機械学習を勉強したことのある人であれば読めるように書いたつもりです。
モデルには高校基礎レベルの物理(円運動)と大学1年生レベルの数学(行列、微分方程式)を使っているので、詳しく知りたい方はまずこれらをざっくり学習することをお勧めします。
使用した環境は以下のとおりです。
Google Colaboratory
python 3.7
pytorch 1.7.1+cu101
torchdiffeq 0.2.1
1. モデル予測制御とは
モデル予測制御とは各時刻で未来の応答を予測しながら最適化を行う制御手法です。(モデル予測制御(MathWorks)より引用)
今回は自動車のハンドルを制御して、レーンをはみださずに自動車を走らせることを目標とします。以下の1~3を繰り返して自動車を制御します。
- モデルを使って自動車の挙動を予測する
- 予測した結果からレーンの中央を通るようにハンドルを制御する
- 自動車を動かし、位置と速度を更新する
2. 今回使ったもの
2. 1 モデル
ここでは自動車は速度一定で走行するとします。また、ハンドルを角度 $\omega$ だけ回したときは角速度 $\omega$ で円運動すると仮定します。角速度とは円運動をする物体が単位時間あたりに回転する角度のことです。例として4秒で一周する物体の角速度は $2\pi/4 = \pi/2 \quad[rad/s]$ となります。このとき自動車の現在の位置と速度、および角速度がわかれば、現在からt秒間の位置と速度を計算することが可能です。円運動は以下の微分方程式で記述されるため、$t$ 秒後の位置と速度は常微分方程式を解いて求めていきます。
$$
\frac{d^2 x_1}{dt^2}=-\omega^2 x_1, \frac{d^2 x_2}{dt^2}=-\omega^2 x_2
$$
ここで、$x_1$、$x_2$は座標です。また、角速度は左に曲がるときに正、右に曲がるときに負の値をとるとします。円運動の中心は原点($(x_1, x_2) =(0,0)$となる点)です。
計算を簡単にするため、1階の微分方程式として記述したいので、$\boldsymbol{x}$を以下のように定義します。
$$
\boldsymbol{x}=
\begin{pmatrix}
x_1\
x_2\
\dot{x}_1\
\dot{x}_2
\end{pmatrix}
$$
ここで $\dot{x}_1$, $\dot{x_2}$ はそれぞれ $x_1$、$x_2$ の時間微分を表しており、速度と同義です。
行列を使ってこの $\boldsymbol{x}$に関する微分方程式を以下のように書きます。
$$
\frac{d\boldsymbol{x}}{dt}=\boldsymbol{A}\cdot \boldsymbol{x}
\tag{1}\
\boldsymbol{A}=\begin{pmatrix}
0&0&1&0\
0&0&0&1\
-\omega^2&0&0&0\
0&-\omega^2&0&0
\end{pmatrix}
$$
積分の初期値 $\boldsymbol{x}_0$ は、$x_1$、$x_2$、$\dot{x}_1$、$\dot{x_2}$ の初期値 $x^0_1$、$x^0_2$、$\dot{x}^0_1$、$\dot{x}^0_2$ を用いて以下のように記述します。
$$
\boldsymbol{x}_0 =
\begin{pmatrix}
x^0_1\
x^0_2\
\dot{x}^0_1\
\dot{x}^0_2
\end{pmatrix}
$$
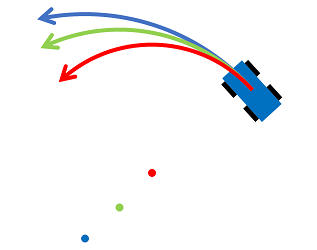
ここで用いた座標系の原点は円運動の中心であり、自動車が動くとともに動きます。自動車が動いたり角速度が変化したりすると円運動の中心が変わるからです。これを下図に示します。ここでは矢印が軌跡、軌跡と同じ色の点が中心を表しています。
しかし、レーンは自動車が動いても動きません。そのため、自動車が動いても動かない座標が必要になります。自動車とともに動く座標を相対座標、動かない座標を絶対座標と呼び、絶対座標を区別するために $\bar{x}_1$、$\bar{x}_2$ と書くことにします。相対座標は今まで通り $x_1$、$x_2$ と表記します。相対座標は絶対座標に対して平行とします。これにより、座標変換の前後で速度ベクトルが変化しないので、座標変換では位置のみを考えればよくなります。
このように定義すると初期値 $\boldsymbol{x}_0$ は、絶対座標における現在地および速度 $\bar{x}^0_1$、$\bar{x}^0_2$、$\dot{\bar{x}}^0_1$、$\dot{\bar{x}}^0_2$ を用いて以下のように記述できます(詳しい導出はAppendixを参照してください)。
$$
\boldsymbol{x}_0=\boldsymbol{T}\cdot\bar{\boldsymbol{x}}_0
\tag{2}\
\boldsymbol{T} =
\begin{pmatrix}
0&0&0&1/\omega\
0&0&-1/\omega&0\
0&0&1&0\
0&0&0&1
\end{pmatrix}\
\bar{\boldsymbol{x}}_0=
\begin{pmatrix}
\bar{x}^0_1\
\bar{x}^0_2\
\dot{\bar{x}}^0_1\
\dot{\bar{x}}^0_2
\end{pmatrix}
$$
また、$\omega = 0$ のときには $\boldsymbol{T}$ が定義できないので、$\omega = 0$ (実際のプログラムでは $|\omega| \lt 10^{-4}$ ) のとき、$\boldsymbol{x}_0 = \bar{\boldsymbol{x}}_0$ とします。
相対座標から絶対座標への変換は次式のとおりです。
$$
\begin{pmatrix}
\bar{x}_1\
\bar{x}_2\
\dot{\bar{x}}_1\
\dot{\bar{x}}_2
\end{pmatrix} =
\begin{pmatrix}
x_1\
x_2\
\dot{x_1}\
\dot{x_2}
\end{pmatrix} - \boldsymbol{x}_0 +
\begin{pmatrix}
\bar{x}^0_1\
\bar{x}^0_2\
\dot{\bar{x}}^0_1\
\dot{\bar{x}}^0_2
\end{pmatrix}
\tag{3}
$$
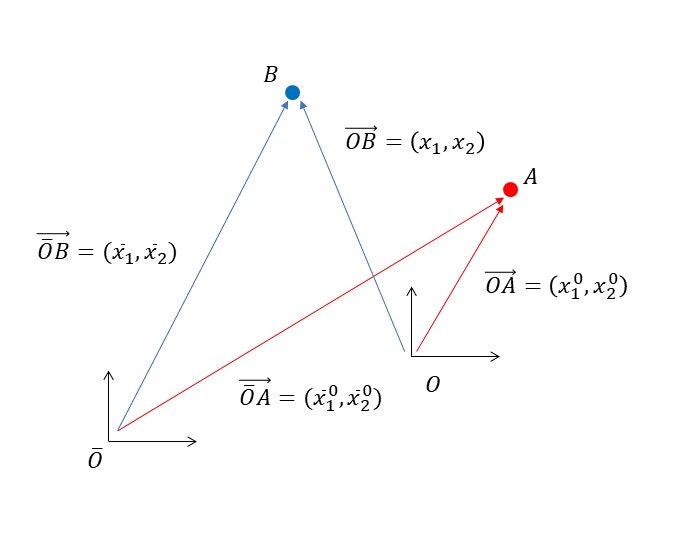
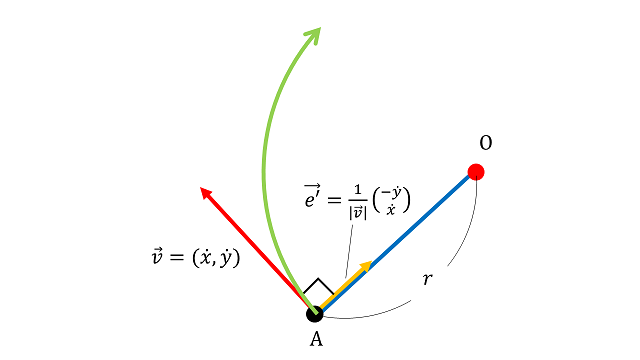
ここで $O$ は相対座標の原点、$\bar{O}$ は絶対座標の原点、$A$ は初期値、$B$ は自由にとった点です。(3)式の各要素に相当するベクトルは以下のようになります。
$$
\begin{pmatrix}\bar{x}_1\\ \bar{x}_2\end{pmatrix}=\vec{\bar{O}B},
\begin{pmatrix}x_1\\ x_2\end{pmatrix}=\vec{OB},
\begin{pmatrix}\bar{x}^0_1\\ \bar{x}^0_2\end{pmatrix}=\vec{\bar{O}A},
\begin{pmatrix}x^0_1\\ x^0_2\end{pmatrix}=\vec{OA},
$$
これより以下の式が成り立ちます。
\begin{align}
\begin{pmatrix}
\bar{x}_1 \\
\bar{x}_2
\end{pmatrix}
&= \vec{\bar{O}B} \\
&= \vec{OB}-\vec{O\bar{O}} \\
&= \vec{OB}-\left\{\vec{A\bar{O}}-\vec{AO}\right\} \\
&= \vec{OB}-\left\{\vec{OA}-\vec{\bar{O}A}\right\} \\
&= \begin{pmatrix}
x_1 \\
x_2
\end{pmatrix} -
\begin{pmatrix}
x^0_1 \\
x^0_2
\end{pmatrix} +
\begin{pmatrix}
\bar{x}^0_1 \\
\bar{x}^0_2
\end{pmatrix}
\end{align}
速度は座標系によらないので上式から(3)式が成り立ちます。
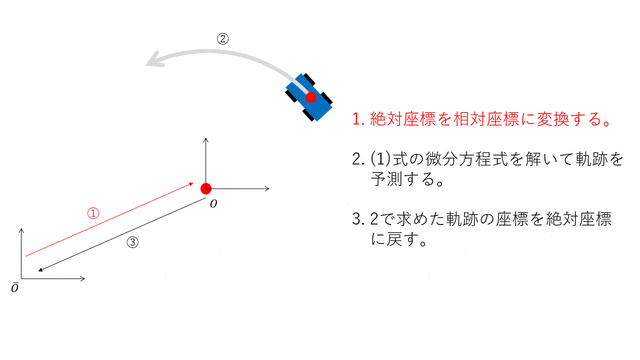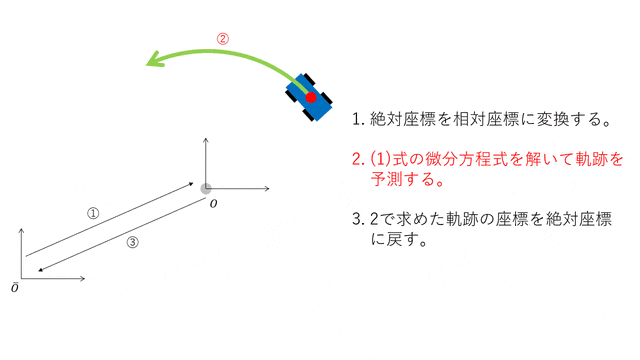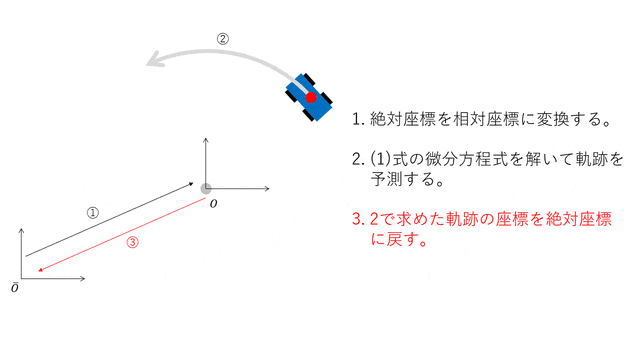
以上を用いて自動車の軌跡を予則する方法を以下に示します。
- 絶対座標を相対座標に変換する。
- (1)式の微分方程式を解いて軌跡を予測する。
- 2で求めた軌跡の座標を絶対座標に戻す。
図にすると以下のようになります。
これらを計算する関数のコードは以下のようになります。
def model(omega, pos, vel, t):
"""
t秒間の自動車の位置と速度を返す関数
自動車の動きは単純な円運動を仮定する
omega: 自動車の角速度 [rad/s]
pos: 自動車の現在位置[m, m]
vel: 自動車の速度 [m/s, m/s]
t: 予測するステップ数 [count]
"""
def func(t, x):
"""円運動を記述する微分方程式の右辺"""
A = -tensor([[0, 0, 0, 0],[0, 0, 0, 0],[1, 0, 0, 0],[0, 1, 0, 0]])*(omega**2) + tensor([[0, 0, 1, 0],[0, 0, 0, 1],[0, 0, 0, 0],[0, 0, 0, 0]])
out = A @ x
return out
x_global = torch.cat([pos, vel])
# 絶対座標から相対座標への変換
if abs(omega) >= 1e-4:
T = tensor([[0, 0, 0, 1],[0, 0, -1, 0],[0, 0, 0, 0],[0, 0, 0, 0]])/omega + tensor([[0, 0, 0, 0],[0, 0, 0, 0],[0, 0, 1, 0],[0, 0, 0, 1]])
x0 = T @ x_global
else:
# 角速度が0.0001より小さかったら直進する
x0 = x_global
# 微分方程式を解いて円の座標と速度を記述
# odeintはODEソルバーであり、引数に関数、初期値、積分回数を入力することで微分方程式の計算結果を受け取れる
res = odeint(func, x0, t)
res_global = res + x_global - x0 # 相対座標を絶対座標に直す
# 自動車の座標と速度に分解
res_pos = res_global @ tensor([[1, 0], [0, 1], [0, 0], [0, 0]]).float()
res_vel = res_global @ tensor([[0, 0], [0, 0], [1, 0], [0, 1]]).float()
return res_pos, res_vel
2.2 ODEソルバー
では、この微分方程式をどのように解いていけばいいでしょうか。ここでは公開されているライブラリである torchdiffeq 内の odeint を使用していきます。微分方程式を解く関数をODEソルバーと呼びます。torchdiffeq についてはこちらを参照してください。
odeint は上のソースコード中の下から5行目で用いています。odeint は func、x0、tを引数として与えると微分方程式を解き、t の各要素に対する積分値を返します。func は微分方程式の右辺の関数、x0 は初期値、t は積分のステップです。
2.3. 制御手法
以下の方針に基づいて制御していきます。
- 自動車がレーンからはみ出さない
- 自動車が目的地に向かって走る
- 急ハンドルを切らない
まずレーンからはみ出さないように制御する方法を検討します。そのためには、レーンの境界に壁を定義し、これにぶつからないように制御していきます。壁を認識する方法については次節を参照してください。
今回用いた制御手法はポテンシャル法です。これは障害物からの距離が大きいほど小さくなる関数を損失関数として用い、これが最小となるように制御する手法です。今回用いた関数は次式です。
$$
U_{wall} = \frac{1}{2\pi\sigma^2} exp\Bigl(-\frac{d_{wall}}{2\sigma}\Bigr)
$$
ここで $d_{wall}$ は障害物からの距離、$\sigma$ はパラメータです。今回は $\sigma$ の値をレーンの幅の半分としました。
この $U_{wall}$ を認識したすべての障害物の点について計算し、和を取ります。これを使うことで障害物から遠ざかれば遠ざかるほど損失を小さくすることができます。すなわち、レーンの中央を維持することができます。
次に目的地に向かって走る方法を検討します。制御は上記と同様のポテンシャル法です。今回は目的地に近づくほど損失関数が小さくなってほしいので、$U$ の符号を反転します。
$$
U_{goal} = -\frac{1}{2\pi\sigma^2}exp\Bigl(-\frac{d_{goal}}{2\sigma}\Bigr)
$$
ここで $d_{goal}$ は目的地までの距離です。
目標には四隅の中心とし、自動車がこの目標に十分近づいたら次の点を目標とします。
上記の $U_{wall}$、$U_{goal}$ は自動車の軌跡の中の1点での損失の和です。これを軌跡のすべての点について計算し、平均を取ります。
次に急ハンドルを防ぐために、自動車の角速度についてもその大きさに応じて損失を与えていきます。まず角速度が大きくなると大きくなる損失を与え、レーン内を1周するような角速度のときにさらに損失を加えます。
計算式は以下のとおりです。
L_{handle} = \frac{|\omega|\cdot width}{v} \times 0.01 + f(\omega)\\\
f(\omega) = \left\{
\begin{array}{}
\qquad\quad 0 & \Bigl(|\omega|\lt \frac{v}{width}\Bigr)\\\
\Bigr(\frac{|\omega|\cdot width}{v}-1\Bigl)^2 &\Bigl(|\omega|\geq \frac{v}{width}\Bigr)
\end{array}
\right.
$width$ はレーン幅、 $v$ は自動車の速度を表します。レーン幅を1周するときの角速度は $|\omega|=\frac{v}{width}$ より、$\omega$ の絶対値がこれよりも大きくなると $f(\omega)$ が正の値を持ち損失も大きくなります。
求めた $U_{wall}$、$U_{goal}$、$L_{handle}$ を合計したものが損失となります。
$$
Loss = U_{wall} + U_{goal} + L_{handle}
$$
損失を計算するコードは以下のとおりとなります。
def loss_func(omega, positions, goal, wall):
"""
損失関数
omega: 自動車の角速度 [rad]
positions: 自動車の座標を記述した行列 [m, m]*n
goal: 目的地の座標 [m, m]
wall: 壁の座標 [m, m]*m
"""
n = len(positions)
A = tensor([1, 1]).float()
# 自動車がレーンからはみ出ない + 自動車が目的地に向かう
U_wall = 0
U_goal = 0
sigma = HALF_WIDTH
for pos in positions:
dis_wall = ((wall-pos)**2 @ A).sqrt() # 壁からの距離
dis_goal = ((goal-pos)**2 @ A).sqrt() # 目的地からの距離
U_wall += (torch.exp(-dis_wall/sigma) / (2*PI*sigma**2)).sum()
U_goal -= (torch.exp(-dis_goal/sigma) / (2*PI*sigma**2)).sum()
U_wall /= n
U_goal /= n
# 急ハンドルを切らない
L_handle = abs(omega*HALF_WIDTH/VELOCITY)*0.01
# ハンドルの角度が一定以上超えたら損失を大きくする
L_handle += max((abs(omega*HALF_WIDTH/VELOCITY)-1), 0)**2
loss = U_wall + U_goal + L_handle
return loss
上のコードでは、ハンドルの角度が一定以上になるかどうかを判定するときに場合分けをせずにmaxを使っています(下から4行目)。
これはPytorchの自動微分機能をより有効に使えるようにするためです。
2.4. 障害物の認識手法
障害物の認識にはセンサを用いると仮定します。一定間隔で点を取っていき、レーンからはみ出たときの座標を壁の座標とします。この点は自動車を中心に放射状に出ており、左右90°にある壁を認識できるものとします。一定の長さよりも遠い壁は認識できません。
自動車が壁を認識する様子は下図のとおりです。
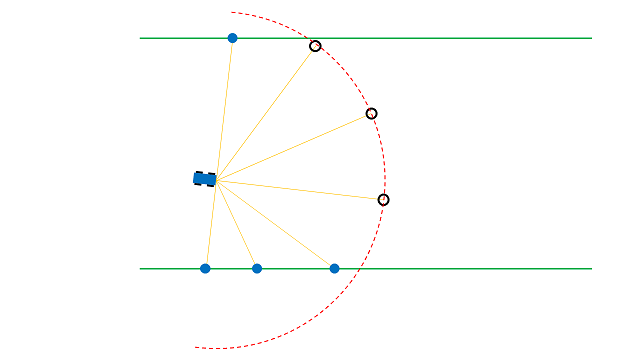
緑の直線が壁、黄色の線がセンサが通過した点、青の点が壁と認識した点、赤の点線が認識できる長さの限界、黒丸は壁を認識できなかった点を表します。
3. 実行結果
ソースコードはこちら(Google Colaboratoryへのリンク)です。
自動車の進み方は以下のとおりです
- 現在の座標と速度から $t_1$ 秒間の自動車の挙動を予測する
- 予測した結果からレーンの中央を通るように角速度を更新する
- 更新した角速度から自動車の挙動を予測する
- 上記2,3を繰り返し最適な角速度を決定する
- 決定した角速度から $t_2$ 秒間走る
- 5で走り終わった座標と速度を1の現在の座標と速度にする
- 1~6を繰り返す
まず、step 1のときの各点における損失のグラフを以下に示します。
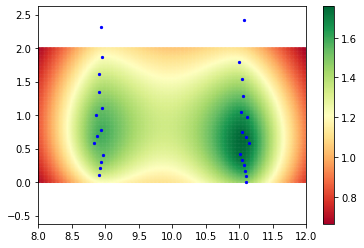
この図よりレーンの中央の損失が小さく、壁に近づくほど損失が大きくなることがわかります。自動車は損失が小さくなるように進むので、壁から離れてレーン中央で走ることが期待できます。
実行した結果は以下のとおりです。緑の点線が壁を表しています。黄色の点がセンサが通過した点、青の点が認識した壁、赤の実線が予測した経路、緑の実践が実際に走行した経路、青の実線が自動車の軌跡をそれぞれ表しています。レーン上の赤点が目標を示しており、自動車がこの点の付近を通過したら次の角が目標となっていることが確認できます。
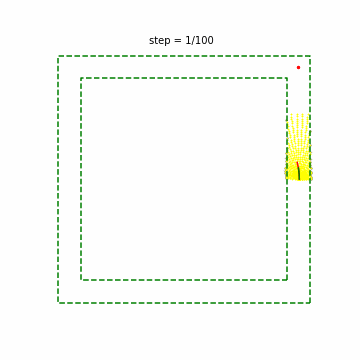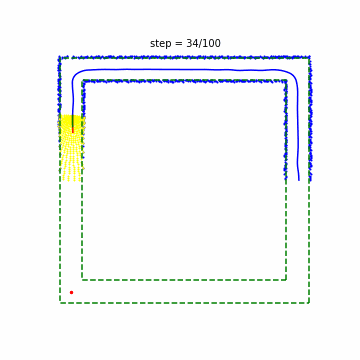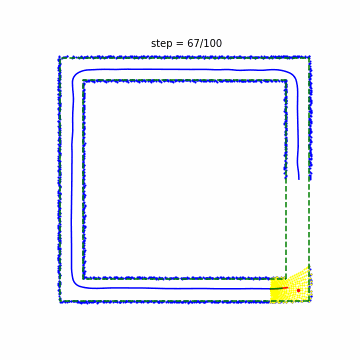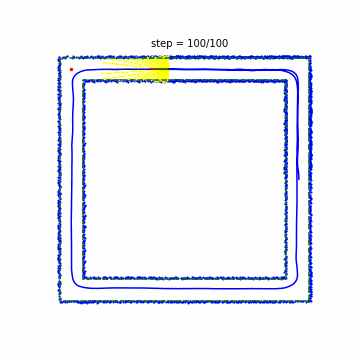
これを見ると、ところどころジグザグに動いており挙動が不安定なところがありますが(例:step 91)、大方うまく制御できているように見えます。
4. 課題
今回はモデルをあらかじめ設定しました。実際に自動車が走行するときには、自動車の形状や路面の状況によって運動の様子が変化します。そのため、角速度に対応する運動の様子を教師データとしてモデルを学習する必要があります。今後はこのことを考慮して、モデルの学習を行いつつ制御していきたいです。
また、今回制御したのは角速度(ハンドル)のみです。しかし、あなたが車を運転するときに制御しているのはハンドルだけではないですよね?速度も制御します。急カーブでは速度を落としますし、広い直線道路では速度を上げます。今後は速度も制御していきたいと考えています。とくに今回のような矩形の道路を考える場合、角では速度を落とし、直線でまた上げるような制御をしたいです。
加えて、今回レーンとして仮定したレーン幅や自動車の速度は現実とはかけ離れています。そのため、より現実に即した状況で学習を行っていきたいです。
5. 終わりに
モデル予測制御を用いて自動車の運動を制御してみました。課題はまだまだありますが、ひとまずレーンをはみ出さずに走らせることができました。
Appendix
A1. (2)式の導出
(2)式を導出していきます。まず前提条件を確認します。
- 円運動の中心を原点とした座標を相対座標、自動車の位置に関わらず固定された座標を絶対座標とする。
- 相対座標は絶対座標を平行移動したものである。
- 条件2より、速度は座標によらない。
- 現在地は初期値に対応する位置と同じである。
手順は以下のとおりです。
- 現在地と現在の速度および角速度から 円の中心の座標を絶対座標上で求める。
- 円の中心が原点となるように絶対座標の原点を平行移動する。
- 現在地について中心からの相対座標を求める。
ここでは絶対座標の原点を $\bar{O}$、相対座標の原点を$O$、現在地を $A$ とします。
1. 現在地と現在の速度および角速度から 円の中心の座標を絶対座標上で求める。
まず中心までの距離を求めます。これは $r=\frac{v}{|\omega|}$ となります。$r$ は円運動の半径、$v$ は速さ(スカラー)です。
次に初期値から中心までの方向を求めます。
最初に左に曲がる場合を考えます。このとき、円運動の中心は進行方向に対して左手に90°の方向にあります。
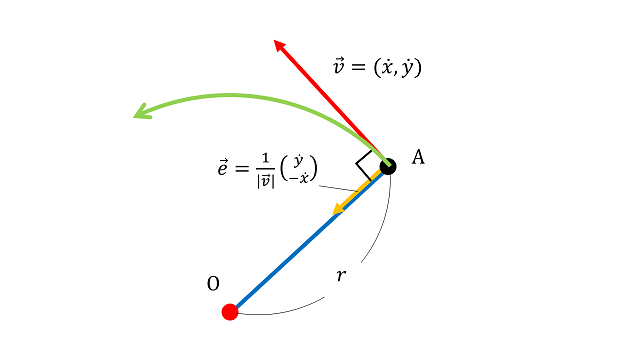
速度ベクトルは $(\dot{\bar{x}}_1, \dot{\bar{x}}_2)$ であり、これを左手方向に90°回転したベクトルは $(-\dot{\bar{x}}_2, \dot{\bar{x}}_1)$ となります。
ここで、ベクトル$(s,t)$を角度 $\theta$ だけ回転する方法を説明します。
回転を表す行列は次のとおりです。
\boldsymbol{T}_{\theta}=\begin{pmatrix}
cos \theta &-sin \theta \\
sin \theta & cos \theta
\end{pmatrix}
これをもとのベクトルの左からかけると、ベクトルを $\theta$ だけ回転したベクトル$\boldsymbol{R}$を求めるとことができます。
\begin{align}
\boldsymbol{R}&=\boldsymbol{T}_{\theta} \begin{pmatrix} s\\ t \end{pmatrix} \\
&=\begin{pmatrix}
cos \theta &-sin \theta \\
sin \theta & cos \theta
\end{pmatrix} \begin{pmatrix} s\\ t \end{pmatrix} \\
&=\begin{pmatrix}
s \cdot cos \theta - t \cdot sin \theta \\
s \cdot sin \theta + t \cdot cos \theta
\end{pmatrix} \\
\end{align}
これに$\theta=90°$を代入し、元のベクトルを速度にすれば、速度ベクトルを左手方向に90°回転したベクトルが $(-\dot{\bar{x}}_2, \dot{\bar{x}}_1)$ と求まります。
$\vec{AO}$ の単位ベクトル $\boldsymbol{e}$ は $\boldsymbol{e}=\frac{1}{v}(-\dot{\bar{x}}_2, \dot{\bar{x}}_1)$ です。単位ベクトルとは長さが1で同じ方向のベクトルのことです(上図黄色の矢印)。これより $\vec{AO}$ は
\begin{align}
\vec{AO} &= r \cdot \boldsymbol{e} \\
&= \frac{v}{|\omega|} \cdot
\frac{1}{v} \cdot
\begin{pmatrix}
0 & -1 \\
1 & 0
\end{pmatrix} \cdot
\begin{pmatrix}
\dot{\bar{x}}_1 \\
\dot{\bar{x}}_2
\end{pmatrix} \\
&= \frac{1}{\omega} \cdot
\begin{pmatrix}
-\dot{\bar{x}}_2 \\
\dot{\bar{x}}_1
\end{pmatrix} \tag{A1}
\end{align}
左に曲がるときは $\omega\gt0$ となるので、これを利用して絶対値記号を外しました。
このとき、速度ベクトルを右手に90°回転したベクトルの単位ベクトルは $\frac{1}{v}(\dot{\bar{x}}_2, -\dot{\bar{x}}_1)$ となります。これより $\vec{AO}$ は
\begin{align}
\vec{AO} &= r\cdot\boldsymbol{e} \\
&= \frac{v}{|\omega|}\cdot
\frac{1}{v} \cdot
\begin{pmatrix}
0 & 1 \\
-1 & 0
\end{pmatrix} \cdot
\begin{pmatrix}
\dot{\bar{x}}_1 \\
\dot{\bar{x}}_2
\end{pmatrix} \\
&= \frac{1}{-\omega}\cdot
\begin{pmatrix}
\dot{\bar{x}}_2 \\
-\dot{\bar{x}}_1
\end{pmatrix} \\
&= \frac{1}{\omega}
\begin{pmatrix}
-\dot{\bar{x}}_2 \\
\dot{\bar{x}}_1
\end{pmatrix} \tag{A2}
\end{align}
ここで $\omega\lt0$ を利用して絶対値記号を外しました。(A1)と(A2)を比較するとどちらの場合も初期値から中心へのベクトルは $\vec{AO}=\frac{1}{\omega}(-\dot{\bar{x}}_2, \dot{\bar{x}}_1)$ となっていることがわかります。中心の絶対座標 $(\bar{O}_1, \bar{O}_2)$ は $\vec{\bar{O}O}$ と等しく、以下のように書けます。
\begin{align}{}
\begin{pmatrix}
\bar{O}_1 \\
\bar{O}_2
\end{pmatrix} &= \vec{\bar{O}O} \\
&= \vec{\bar{O}A}+\vec{AO} \\
&= \begin{pmatrix}
\bar{x}^0_1 \\
\bar{x}^0_2
\end{pmatrix} + \frac{1}{\omega}
\begin{pmatrix}
-\dot{\bar{x}}_2 \\
\dot{\bar{x}}_1
\end{pmatrix}
\end{align}
これより円の中心の絶対座標が求まりました。
2. 円の中心が原点となるように絶対座標の原点を平行移動する。
すべての絶対座標上の点 $(\bar{x}_1, \bar{x}_2)$ を相対座標上の点 $(x_1, x_2)$ に移すには
\begin{align}
\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix} &=
\begin{pmatrix}
\bar{x}_1 \\
\bar{x}_2
\end{pmatrix} -
\begin{pmatrix}
\bar{O}_1 \\
\bar{O}_2
\end{pmatrix} \\
&= \begin{pmatrix}
\bar{x}_1 \\
\bar{x}_2
\end{pmatrix} -
\left\{
\begin{pmatrix}
\bar{x}^0_1 \\
\bar{x}^0_2
\end{pmatrix} + \frac{1}{\omega}
\begin{pmatrix}
-\dot{\bar{x}}_2 \\
\dot{\bar{x}}_1
\end{pmatrix}
\right\} \tag{A3}
\end{align}
とすればよいです。
3. 現在地について中心からの相対座標を求める。
2で求めた(A3)式に $\bar{x}_1=\bar{x}^0_1$ 、$\bar{x}_2=\bar{x}^0_2$ を代入して初期値の相対座標を求めます。
\begin{align}
\begin{pmatrix}
x^0_1\\\
x^0_2
\end{pmatrix} &=
\begin{pmatrix}
\bar{x}^0_1\\\
\bar{x}^0_2
\end{pmatrix} -
\left\{
\begin{pmatrix}
\bar{x}^0_1\\\
\bar{x}^0_2
\end{pmatrix} + \frac{1}{\omega}
\begin{pmatrix}
-\dot{\bar{x}}_2\\\
\dot{\bar{x}}_1
\end{pmatrix}
\right\}\\\ &= \frac{1}{\omega}
\begin{pmatrix}
\dot{\bar{x}}_2\\\
-\dot{\bar{x}}_1
\end{pmatrix}
\end{align}\tag{A4}
以上により相対座標における現在地の座標を求めることができました。
速度は座標変換の影響を受けないので、積分の初期値 $\boldsymbol{x}_0$ は以下のようになります。
$$
\boldsymbol{x}_0 =
\begin{pmatrix}
0&0&0&1/\omega\
0&0&-1/\omega&0\
0&0&1&0\
0&0&0&1
\end{pmatrix} \cdot
\begin{pmatrix}
\bar{x}^0_1\
\bar{x}^0_2\
\dot{\bar{x}}^0_1\
\dot{\bar{x}}^0_2
\end{pmatrix}
$$
これより(2)式を導くことができました。
察しのいい方はもうお気づきかもしれませんが、実は手順の1で中心の座標を決定した時点で相対座標を求めることが可能です。
初期値の相対座標は $\vec{OA}$ であり、これは $\vec{OA}=-\vec{AO}$ と書きなおせます。そして $\vec{AO}$ は手順1で計算しているため、これで相対座標に直すことができます。実際、(A1)、(A2)で求めたものの符号を反転すれば(A4)に一致します。
(この記事は研究室インターンで取り組みました:https://kojima-r.github.io/kojima/)