"pymc3 状態空間モデル" とか "pymc3 state space model" でググると、状態方程式(ここでは最も基本的な "ランダムウォーク + ノイズ" のいわゆるローカルレベルモデルとする)の1つ1つの状態変数に Normal() を割り当てている、つまり
import pymc3 as pm
...
with pm.Model() as model:
...
# y は入力の時系列データ
# 本当は i == 0 (初期状態) の時に場合分けをしないといけないが、ここでは雰囲気だけ掴むために省略
# 気になる人は上のキーワードでググってください
states = [pm.Normal(name=f"state{i}", mu=states[i - 1], ...) for i in range(len(y))]
obs = pm.Normal(name='obs', mu=states, observed=y, ...)
みたいにしている実装しか見当たらなかった。PyMC は変数の数が増えると実行時間がすごい勢いで遅くなっていくので、このようなやり方だと時系列の長さのオーダーが 1,000 を超えたあたりから普通のマシンではとても辛くなってくる。
PyMC3 ではこのような場合に代わりに pm.GaussianRandomWalk() を使用することを推奨している。が、これを使った(少なくともシンプルな)実装が見当たらなかったので書いた(公式ドキュメントにあっても良さそうな気もするのですが)。このメソッドは、上のような(標準)正規分布に従う変数のリストを、あたかも1つの変数として扱うことを可能とする。実行時間もとても速くなる。
以下のベタ書きコードでは、状態誤差(遷移)が平均 0 標準偏差 3 の正規分布、観測誤差が平均 0 標準偏差 1 の正規分布に従うような長さ 100 の時系列データ y に対してローカルレベル状態空間モデルをベイズ推定している。ベイズ的でない普通の(?)フィッティングがしたい場合は、例えば statsmodels.api.tsa.UnobservedComponents() のカルマンフィルタを使う方法が高速だし標準的だろう。こちらはググると大量の記事が見つかるので割愛。
import numpy as np
import pymc3 as pm
import matplotlib.pyplot as plt
# "観測時系列データ" の生成
y = np.cumsum(np.random.normal(scale=3, size=100)) + np.random.normal(scale=1, size=100)
plt.plot(y) # 乱数のシードを固定していないので実行のたびに結果は変わる
plt.show()
with pm.Model() as model:
# 状態誤差が従う正規分布の標準偏差の事前分布
state_sd = pm.InverseGamma('state_sd', alpha=1.0, beta=1.0)
# ここが主題。各状態ごとの正規分布のリストの代わりに、用意されている便利な "ランダムウォークの分布" を使う
state = pm.GaussianRandomWalk('state', sd=state_sd, shape=len(y))
# 観測誤差が従う正規分布の標準偏差の事前分布
obs_sd = pm.InverseGamma('obs_sd', alpha=1.0, beta=1.0)
# 観測値を生成するモデル
obs = pm.Normal('obs', mu=state, sd=obs_sd, observed=y)
事前分布はある程度なんでも良いはずだが、最初に状態誤差・観測誤差それぞれ pm.Uniform('...', 0, 10) とかにしたら変なことになった。
以下の一文で作ったモデルをグラフィカルモデル的に表示できる。
pm.model_to_graphviz(model)
今回のモデルだとこうなる。

推定の実行および結果の表示は以下の通り。
# サンプリングの実行(モデルのパラメタ推定)
with model:
trace = pm.sample()
# 推定した変数の事後分布およびサンプリング時の値の遷移の表示
pm.traceplot(trace)
plt.show()
# 推定値やp値などの結果のテーブルが返ってくる
pm.summary(trace) # 結果は省略

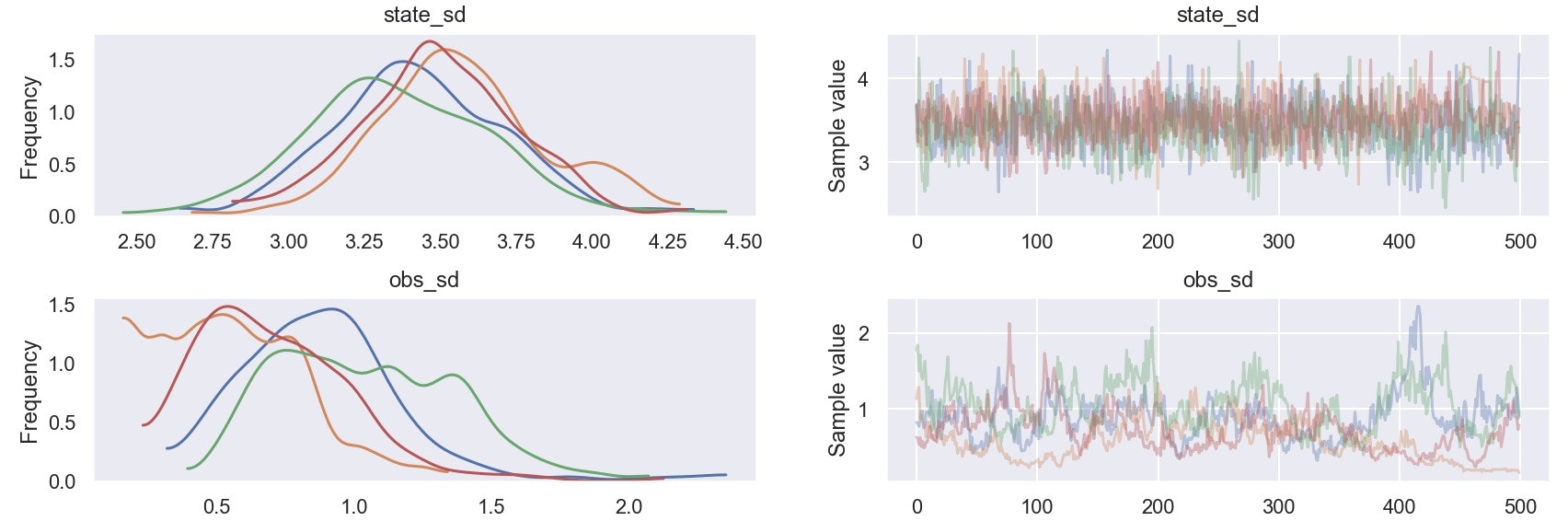
観測誤差の標準偏差の推定があまりよろしくない。どなたかおかしな箇所があったら教えてください。。
(2018/10/13 追記: その後 GaussianRandomWalk() ではなく Normal() のリストを使ったモデルでも学習してみたが、結局のところこちらでも似たような傾向の結果となった(下図; 入力データは上のものとは異なることに注意)。なのでこれはモデルの問題ではなく、今回生成しているデータの本質的な推定の難しさによるものかもしれない。もしくは現在全てデフォルトで実行しているサンプリング pm.sample() をチューニングすれば改善するかも?)