はじめに
昔、「たとえ火の中水の中草の中...」って歌ありましたよね。あの歌うたってた人、今頃どうしてらっしゃるんでしょうね。
そしてたとえ火の中でも水の中でも草の中でも、因果推論という森の中をかけめぐり因果を見つけ出すのがデータサイエンティストというもの。何が何でも因果をゲットしてやるぜ!
因果推論とは
データサイエンス、AI、機械学習などと聞くと、普通は予測モデルを作ったり、画像を生成したりというものを思い浮かべる方が多いと思うのですが、因果推論というジャンルもありまして、これはデータの中にひそむ因果関係を見つけ出してやろうというものです。因果、ゲットだぜ。
そして、このジャンルは「計量経済学」というジャンルとも密接につながっていて、背後にひそむ原因を知ることでそれを経済効果の分析に活かしたり、公共政策に活かしたりできるので、実社会にとっても重要な役割を果たしているんです。
どのようにして因果を推定するのかというと、ある介入が行われた(例えば「広告を出す」など)場合とそうでない場合の、結果(例えば「売上収入」)を比較することで、その介入がどのくらい結果に影響を与えているか調べたりします。これが因果関係です。
Causal Tree, Causal Forestとは
今回行うCausal Tree(因果木)も、計量経済学の手法の一つです。普通因果推論ではATE(平均処置効果)という、全体のデータを通じて介入がどのくらい影響を与えているか、という指標で考えるのですが、Causal Treeの場合は、CATE(条件付き処置効果。Conditional Average Treatment Effect)というものを調べます。ある条件(例えば、お店の規模がどれくらいかや、時期など)での処置効果を見ることで、それぞれ特徴が異なる一つ一つのデータごとに、潜在的な処置効果を調べることができます。これを活用して、個々のデータの異質性を考慮して分析しようという、HTE(Heterogeneous Treatment Effect)という考え方も生まれました。このCATEなどを、決定木のアルゴリズムを使って推定しようというのが、CausalTree(因果木)の考え方です。詳しい方法などはこちらの記事やこちらの記事(因果木ではなくCATEやMetaLearnersについて)などが詳しいので是非どうぞ。そして、これをランダムフォレストを使って行うのがCausalForestです。(詳しい理論はすみません、まだ勉強中です汗)
EconMLについて
今回は、このCausalTreeを、EconMLというPythonライブラリで実装してみます。EconMLはMicrosoftResearchの研究チームが作成した、計量経済学と機械学習を組み合わせたライブラリのようで、情報は少ないですが、Microsoft直々に出ているコード例などがとても参考になり、また公式ドキュメントも割と充実しています。UserGuideなどは各手法のコード例なども載っていて、とりあえずコードを動かしてみたいというときに役立ちます。余談ですが、Economy(経済学)とMachineLearning(機械学習)でEconMLなのですかね。なかなかのネーミングセンスです。
分析に使うのは、何を隠そう、ポケモンのデータです。本当はどういう従業員が退職するかのHRアナリティクスや最近kaggleでトレンドとして出ていたwalmartのデータなども使ってまじめに分析したのですが、結局ポケモンが一番分かりやすいというかイメージしやすかったのでこれにしました。いつかできたら他の分析も記事にするかもしれません。データはいつものやつを使いました。
分析
実行環境
・Python3
・Windows10
・ノートパソコン
・GoogleColaboratory
データについて
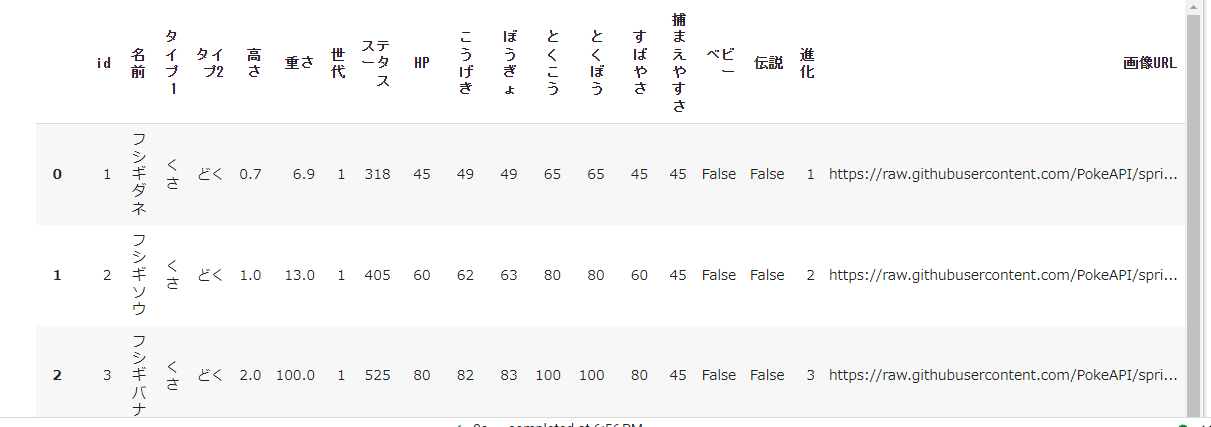
id, 名前, タイプ1, タイプ2, 高さ, 重さ, 世代, ステータス, HP, こうげき, ぼうぎょ, とくこう, とくぼう, すばやさ, 捕まえやすさ, ベビー, 伝説, 進化, 画像URL
というカラムからなる、897行 × 19列のデータです。レイスポスまでいるので、剣盾までですね。画像URLとかも使えそうですが、今回は使いません。
コード
!pip install econml
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import econml
pandasデータフレームの表示行数、列数を設定
pd.set_option('display.max_rows', 100) # 100行まで表示
pd.set_option('display.max_columns', None) # 列(幅)は最大まで表示
# 日本語が使えるmatplotlibのインポート
!pip install japanize-matplotlib
import japanize_matplotlib
from google.colab import drive
drive.mount('/content/drive')
まずEconMLをインストールして、必要なライブラリをインポートして、Googleドライブにマウントしたりしています。この辺りはただの準備です。
そして、先程のデータを読み込みます。パスは実行環境に合わせて適宜変えてください。
# ポケモンのデータ
df = pd.read_csv('/content/drive/MyDrive/MyWorks/data/pokemon_data.csv', encoding='shift-JIS')
display(df)
まず、後に分析で使いたい変数を使ったり、元々ある変数を使いやすい形に変えたりします。
df['ベビー'] = df['ベビー'].astype('int')
df['ベビー'].describe()
df['伝説'] = df['伝説'].astype('int')
df['伝説'].describe()
df['タイプ2'] = df['タイプ2'].fillna('')
df['複合タイプ'] = df['タイプ2'].apply(lambda x: 0 if x == '' else 1)
df['複合タイプ'].describe()
df['BMI'] = df['重さ'] / df['高さ'] ** 2
df['BMI'].describe()
伝説どうかがステータス(合計種族値)にどの程度影響するか、BMIごとに分析
最初に、伝説かどうかを処置(先程の説明でいう「介入」)とし、この伝説かどうかが「ステータス」にどの程度影響を与えるかについて、BMIごとに調べます。ポケモンで「BMI」を算出するという発想、これまで私しか考えたことないのではないでしょうか(ドヤ顔
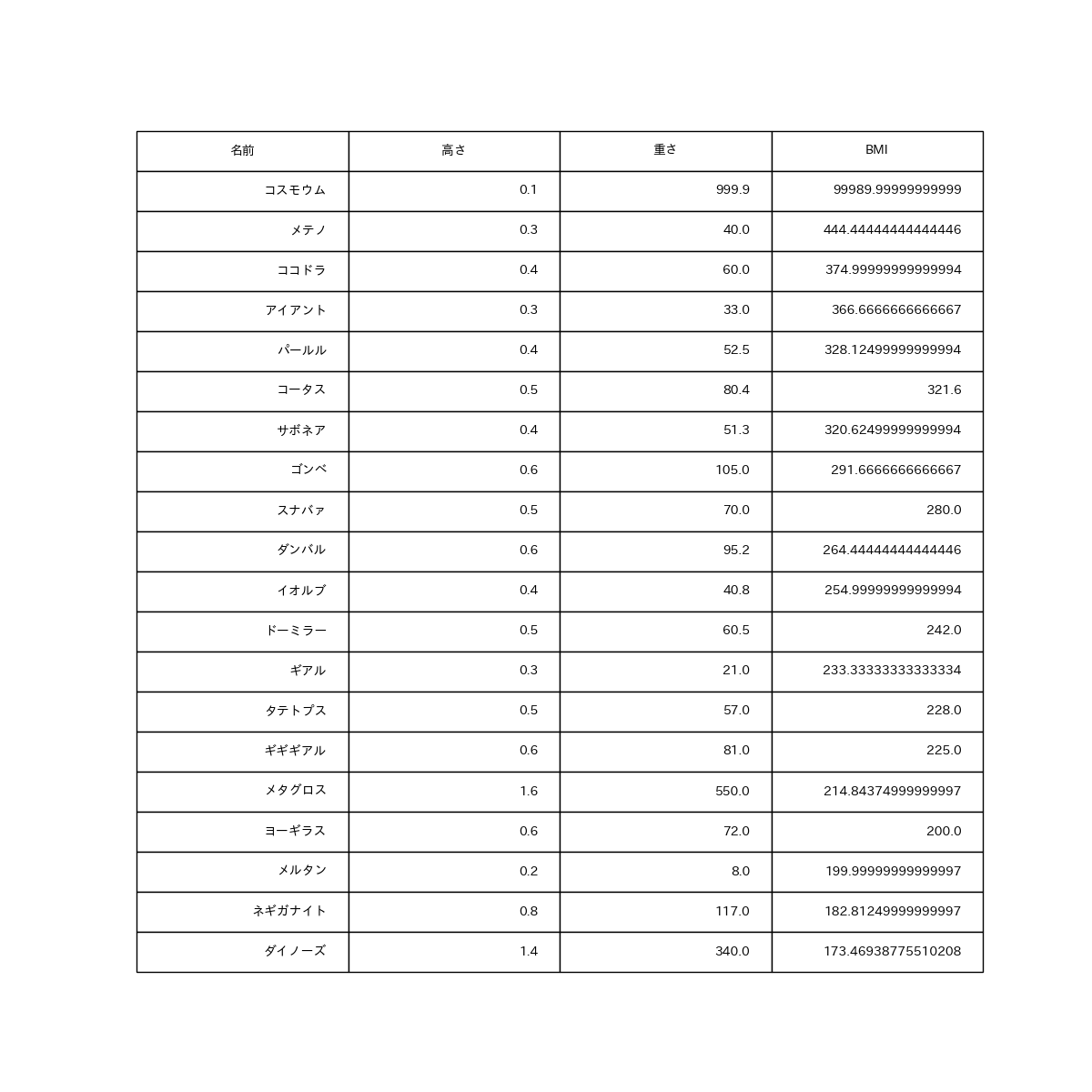
せっかく「BMI」という変数を作ったので、BMIランキングでも見ておきますか。
df.sort_values('BMI', ascending=False).head(20)
コスモウムってメタボなのか...。まぁこれは例外ですかね。アイアントも意外ですね。まあ重いし低いからBMIにすると高くなるのか...。ネギガナイトって(笑)
ちなみにこの画像はこのように出力しました。結構これ便利ですよ。
参考:https://qiita.com/tomyu/items/0fa88b9c4b8fc554dbea
fig, ax = plt.subplots(figsize=(12,12))
ax.axis('off')
ax.axis('tight')
ax.table(cellText=df_BMI[['名前', '高さ', '重さ', 'BMI']].values,
colLabels=df_BMI[['名前', '高さ', '重さ', 'BMI']].columns,
loc='center',
bbox=[0,0,1,1])
plt.savefig('./df_BMI.png')
で、このコスモウムはちょっと異端すぎるというか例外なので、今回は外します。このような外れ値があると、分析結果もそれに引っ張られてしまうので。
# コスモウムはBMIが極端に高すぎる(外れ値)のため、今回ははずす
df2 = df.query('名前 != "コスモウム"')
df2.shape
そろそろ本題に入りますか。やっと今回の分析に使う各変数を定義します。説明変数は今回の場合は条件となる変数、Wは無くて良いのでNone、Tには処置変数として伝説かどうか、そしてYには調べたい結果を設定します。この後EconMLのモデルに突っ込む際に入力できる形に変形してあります。
X = df2[['BMI']].values # 説明変数
W = None # X以外の共変量。今回はなしとする。
T = df2[['伝説']].values # 処置変数
Y = df2['ステータス'].values # 目的変数
Double Machine Learning
参考:
https://econml.azurewebsites.net/_autosummary/econml.dml.DML.html
https://zenn.dev/s1ok69oo/articles/4da9e3b01a0a93
https://cintelligence.co.jp/2020/06/12/blog-causal-inference-5/
ここで何の前触れもなくDoubleMachineLearningという言葉が出てきました。DoubleMachineLearningもCausalTreeの文脈の中で良く出てくるもので、というかEconMLのモデルにたくさんDML(DoubleMachineLearningの略)という単語が出てきますので、結局使うことになると思います。簡単に言うと、処置効果τ(タウ)と目的変数yをそれぞれ予測するモデルを作成し、それらの実際の値と予測値の残差を使って、CATE(条件付き処置効果)を推定するものです。私はこちらの動画で初めて知りました。英語でDoubleMachineLearningについての解説部分は短いですが、端的に説明されていて分かりやすいと思います。ちなみにこちらの動画も日本語でかなり丁寧に解説してくださっているのでおススメです。というかこちらの方AIジョブカレというスクールの先生です。何を隠そう私も授業を受けたことがあります。でもこちらの動画は結構深入った内容まで解説しているので、統計学や機械学習、計量経済学などの前提知識がないと厳しいかもしれません。
ということで、今回はEconMLでこのDoubleMachineLearningを使ってCATEなどを推定します。実際のコードはこんな感じです。
from econml.dml import DML
from econml.sklearn_extensions.linear_model import StatsModelsLinearRegression
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
np.random.seed(123)
est = DML(
model_y=RandomForestRegressor(),
model_t=RandomForestClassifier(),
model_final=StatsModelsLinearRegression(fit_intercept=False),
linear_first_stages=False,
discrete_treatment=True # 処置効果の変数Tをカテゴリー型として扱う(初期値はFalse)
)
est.fit(Y, T, X=X, W=None)
DMLというモデルを使って、yの予測に回帰のランダムフォレスト、tの予測に分類のランダムフォレスト(処置あり、なしの2分類のため)を使っています。最終的な残差同士を使った予測はEconMLの参考コードと同じ、StatsModelsLinearRegressionというものを使っています。あとは普通の機械学習と同じようにfitするだけです。
# 各Xに対する処置効果(τ(X, T0, T1))
tau = est.effect(X, T0=0, T1=1)
tau
array([213.45395195, 213.99218989, 208.0207953 , 208.71192894,
212.64739235, 204.87840917, 202.54701693, 209.26483584,
203.84159662, 204.42690041, 210.40732205, 207.30110243,
202.76817969, 206.63852804, 205.78152233, 210.50887638,
208.12360857, 211.72527158, 201.10945897, 201.67364969,
209.40306257, 207.32966167, 219.60281273, 217.82078813,
201.80059261, 197.13544058, 203.87399351, 205.78152233,
198.69049126, 204.91069395, 202.7943528 , 202.54701693,
208.48155106, 204.72027959, 210.0941962 , 208.6833021 ,
・
・
・
以下略
fitした後のモデルからeffectを取得するだけで、X(今回はBMI)ごとの処置効果τ(タウ)を知ることができます。effect以外にも、ate(平均処置効果)やeffect_interval(効果の信頼区間)など様々な値を取得することができます。早速この取得したτを図示してみます。
plt.title('BMIごとの処置効果')
plt.plot(X, tau)
plt.show()
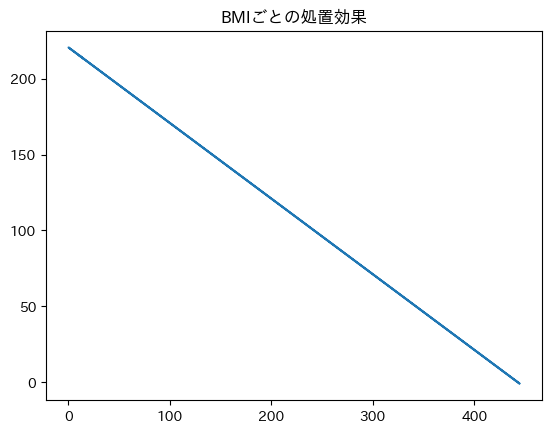
これを見ると、BMIが大きいポケモンほど、推定された処置効果が少ないことが分かります。これを解釈すると、「BMIが大きいポケモンの方が、伝説であることによってステータスへ与える影響が小さい」ということですかね。マナフィみたいな体型のポケモンは合計種族値が...っておっとマナフィに失礼ですね。
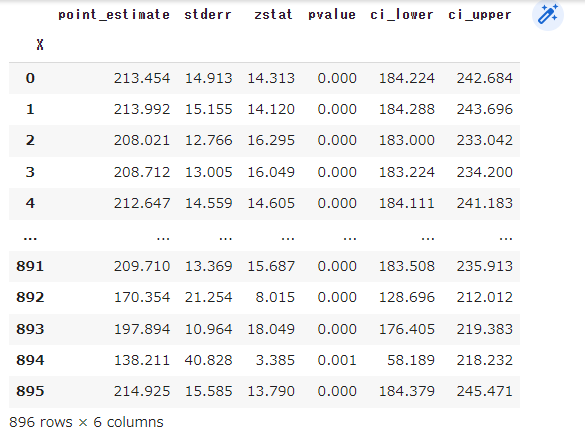
続いて信頼区間なども取得しておきます。Microsoftの参考コードに載っているのですが、summary_frame()とすることで、標準偏差やp値なども一緒にまとめてデータフレームに格納できます。ここでのpoint_estimateが、先程取得したτ(タウ)のことです。
df_summary = est.effect_inference(X, T0=0, T1=1).summary_frame()
df_summary
# ci_lower, ci_upper: 処置効果の信頼区間
また、Rやstats modelなどの統計ツールでおなじみの出力形式でATEについての情報を出すことも可能です。まあここでは平均の効果(mean_point)が200くらいで、p値が0.0ととても小さいので有意とだけ確認しておきましょうか。
# 平均処置効果ATEの情報
est.ate_inference(X)
Uncertainty of Mean Point Estimate
mean_point stderr_mean zstat pvalue ci_mean_lower ci_mean_upper
200.38 11.068 18.104 0.0 178.687 222.074
Distribution of Point Estimate
std_point pct_point_lower pct_point_upper
22.225 144.867 218.802
Total Variance of Point Estimate
stderr_point ci_point_lower ci_point_upper
24.828 136.172 236.795
Honest法を使ったCasualForestDLMで、処置効果の推定
ある程度処置効果がどんな感じか確認できたところで、ようやくCausal Tree, Causal Forestに入っていきます。これも同じようにEconMLのモデルを使っていくだけなのですが、ちょうどHonest法を使ったCausal Forestのやり方がEconMLの公式ドキュメントにありましたので、そちらを参考に実装しました。Honest法についてはこちらの記事に詳しいです。
from econml.dml import CausalForestDML
from sklearn.ensemble import RandomForestRegressor
est = CausalForestDML(model_y=RandomForestRegressor(n_estimators=10, min_samples_leaf=10),
model_t=RandomForestRegressor(n_estimators=10, min_samples_leaf=10),
honest=True, #HONEST法を使う
n_estimators=100, # 木の数
criterion='mse', # 評価指標
max_depth=5, # 木の最大の深さ
min_samples_split=10, # ノードを分割するのに必要な最小限のサンプル数
min_samples_leaf=5 # 各葉のノードに必要な最低限のサンプル数
)
est.fit(Y, T, X=X, W=W)
yを予測するモデルとtを予測するモデルを引数に指定するのは先程と同じで、後はsklearnの決定木やランダムフォレストと同じような作り方です。モデルがCausalForestで内部で指定するモデルもRandomForest二つって、木がいっぱいありそうですね!
後は先程と同じように処置効果について調べていきます。
# 平均処置効果ATE
ATE = est.ate(X)
ATE
196.25188455052256
# 各Xに対する処置効果(τ(X, T0, T1))
# heterogeneous treatment effects(HTE)とも言う。
# 参考:https://www.jstage.jst.go.jp/article/jsaikbs/117/0/117_01/_pdf
tau = est.effect(X)
tau
plt.title('BMIごとの処置効果')
plt.scatter(X, tau)
plt.show()
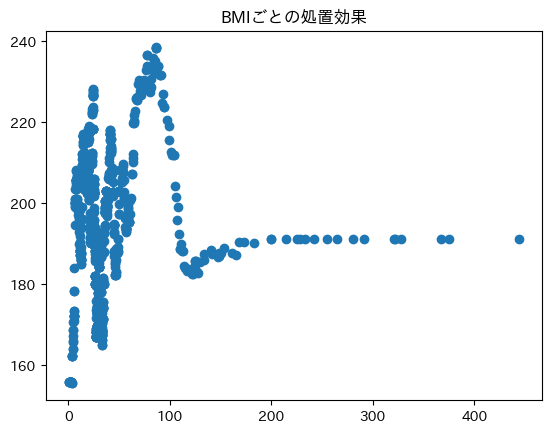
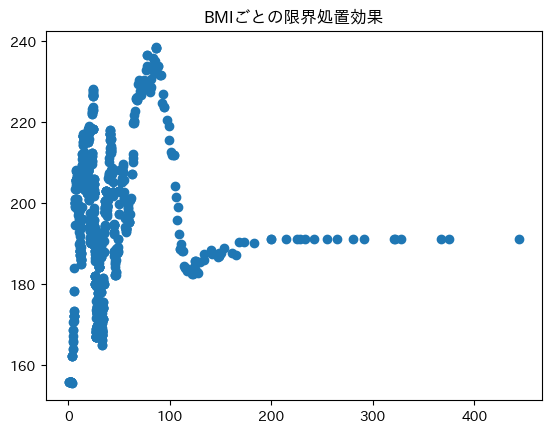
なんかBMIが少ないポケモンは処置効果のばらつきがありそうですね。
続いて、Xごとの処置効果の、変化率も調べます。「限界効果」という、いかにも経済チックな用語でも呼ばれるみたいです。この辺りに経済学とのつながりが感じられますね。元々は顧客分析などに使われる手法のようですしね。
# marginal_effect(限界効果) ∂τ(T, X)
# Xごとの処置効果の勾配(変化率)
# 参考:https://cintelligence.co.jp/2020/06/12/blog-causal-inference-5/
# https://yukiyanai.github.io/jp/classes/econometrics1/contents/R/interaction.html
point = est.const_marginal_effect(X)
point
plt.title('BMIごとの限界処置効果')
plt.scatter(X, point)
plt.show()
ここでもそれぞれについての信頼区間を取得し、せっかくなので合わせて図示してみます。
# 限界効果の信頼区間の下限と上限(有意水準95%)
lb, ub = est.const_marginal_effect_interval(X, alpha=0.05)
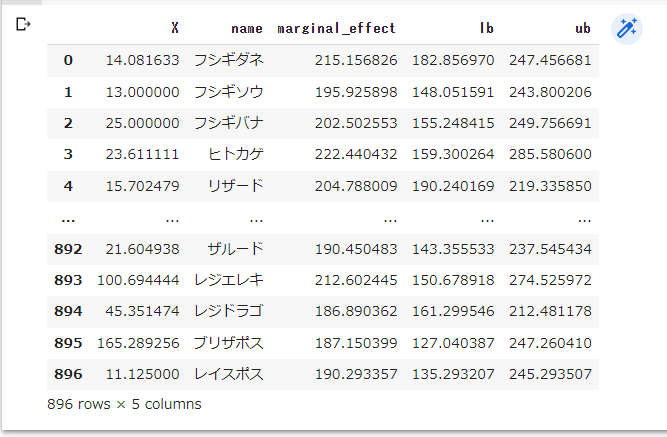
# X、限界効果、信頼区間の下限、上限をデータフレームにまとめる
df_effects = pd.DataFrame(
data={'X': X.reshape(-1,),
'name': df2['名前'],
'marginal_effect': point.reshape(-1,),
'lb': lb.reshape(-1,),
'ub': ub.reshape(-1,)}
)
df_effects
# Xの値で並び替える
df_effects_sorted = df_effects.sort_values('X')
df_effects_sorted
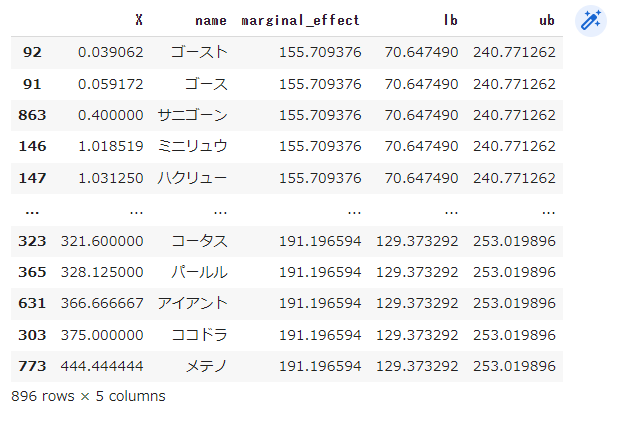
BMIが小さいのはゴースやサニゴーンなのですね。まぁ当たり前か。ミニリュウとハクリュウはさすが...!
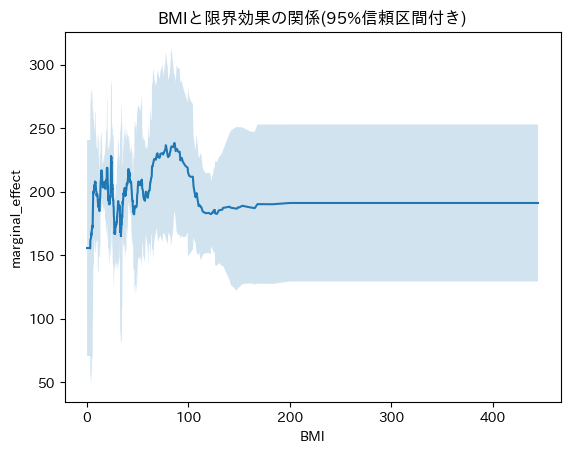
# 信頼区間もまとめて描画
# 参考:https://matplotlib.org/stable/gallery/lines_bars_and_markers/fill_between_demo.html#sphx-glr-gallery-lines-bars-and-markers-fill-between-demo-py
fig, ax = plt.subplots()
plt.title('BMIと限界効果の関係(95%信頼区間付き)')
ax.plot(df_effects_sorted['X'].values, df_effects_sorted['marginal_effect'].values, '-')
# ax.scatter(df_effects_sorted['X'].values, df_effects_sorted['marginal_effect'].values)
ax.fill_between(df_effects_sorted['X'].values, df_effects_sorted['lb'].values, df_effects_sorted['ub'].values, alpha=0.2)
# ax.plot(df_effects_sorted['X'].values, df_effects_sorted['marginal_effect'].values, 'o', color='tab:brown')
ax.set_xlabel('BMI')
ax.set_ylabel('marginal_effect')
plt.show()
ついでに、限界処置効果が小さいポケモン、大きいポケモンがどのようなポケモンかも見てみます。小さいポケモン、大きいポケモン、そんなのひとのかって
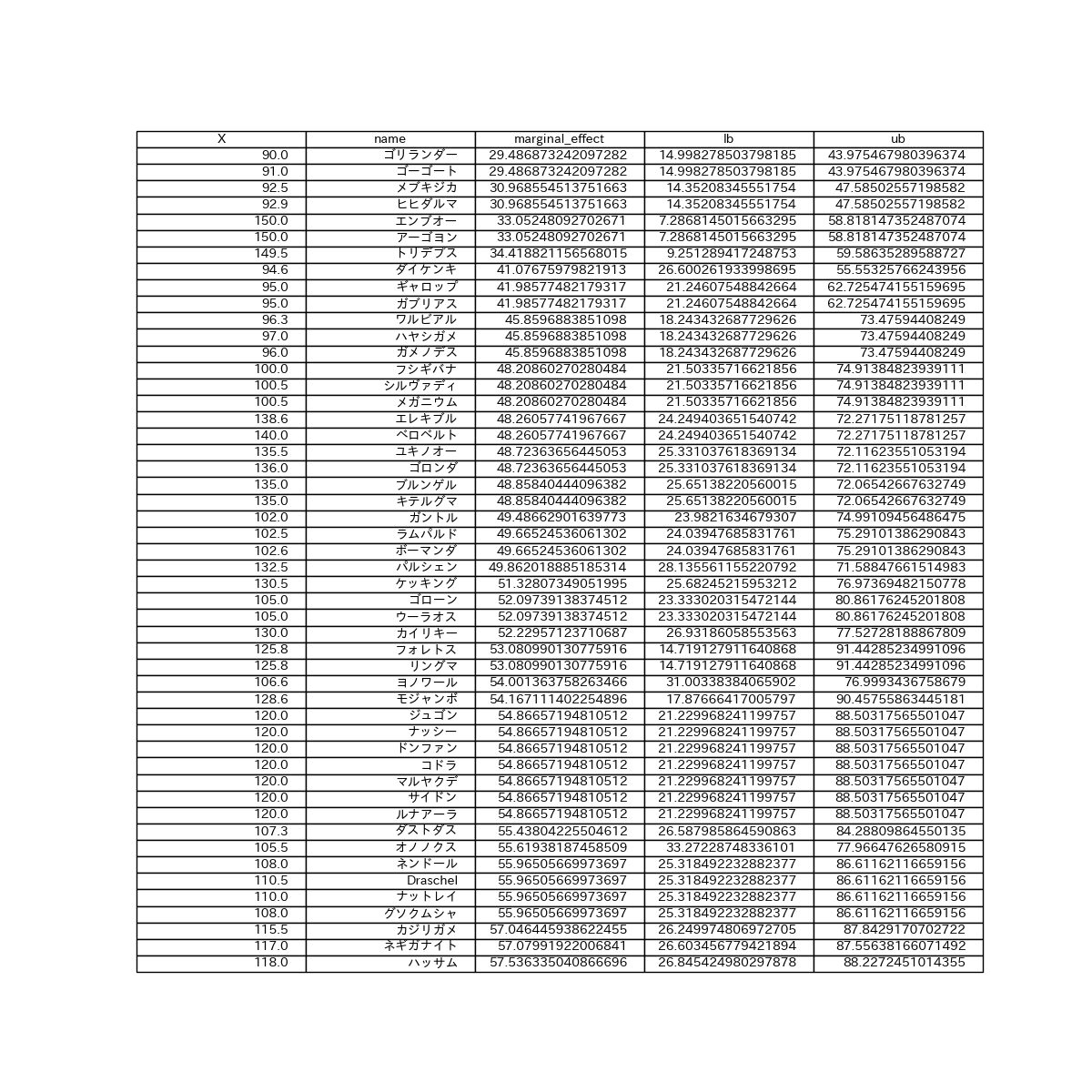
# 限界処置効果が高いポケモン
df_low50 = df_effects.sort_values('marginal_effect').tail(50)
df_low50
fig, ax = plt.subplots(figsize=(12,12))
ax.axis('off')
ax.axis('tight')
ax.table(cellText=df_low50.values,
colLabels=df_low50.columns,
loc='center',
bbox=[0,0,1,1])
plt.savefig('./df_BMI.png')
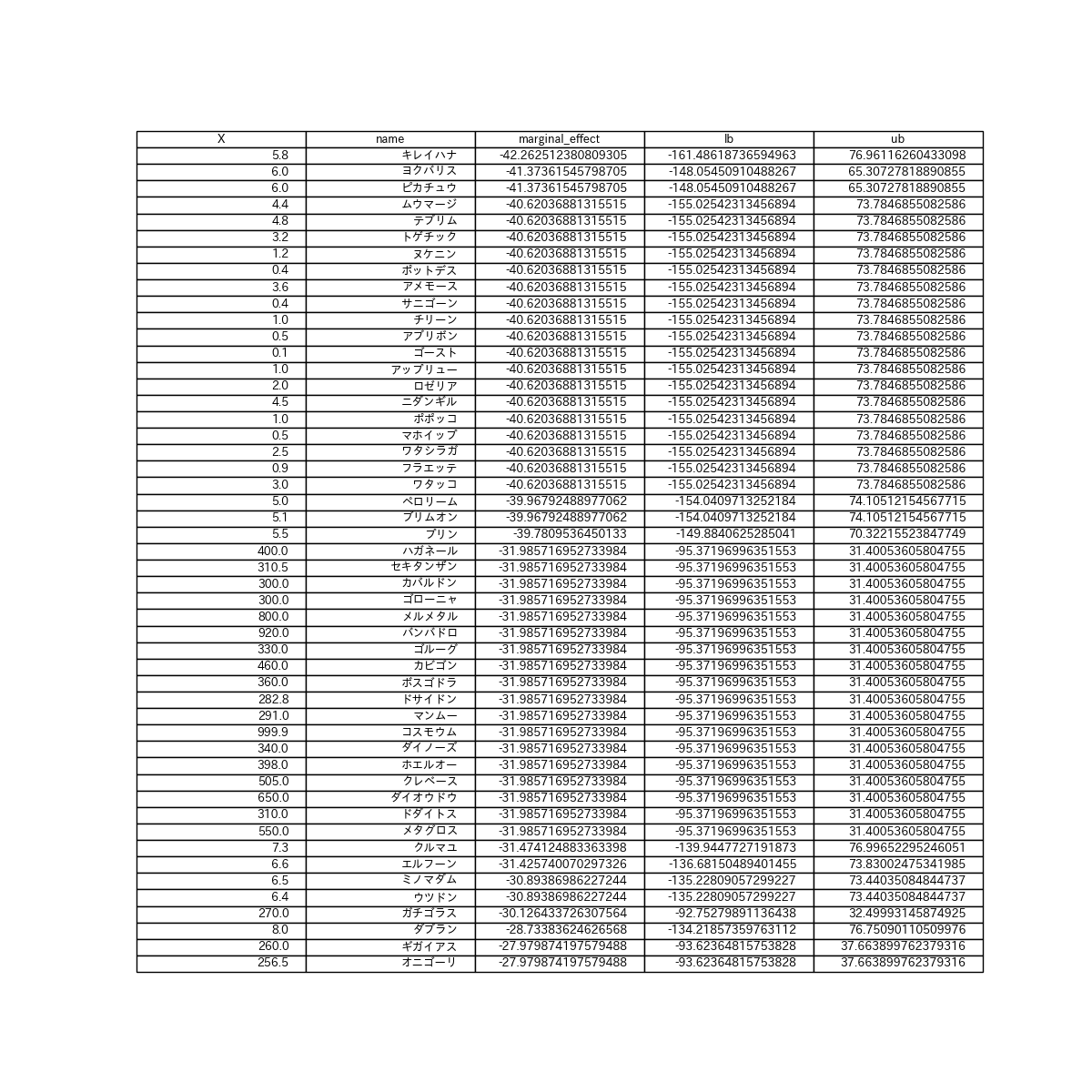
キレイハナは仮に伝説でも弱...ゲフンゲフン。ピカチュウお前もか...。ピカチュウが伝説並みに強いのはアニメだけの話だったんですね。
# 限界処置効果が高いポケモン
df_top50 = df_effects.sort_values('marginal_effect').tail(50)
df_top50
fig, ax = plt.subplots(figsize=(12,12))
ax.axis('off')
ax.axis('tight')
ax.table(cellText=df_top50.values,
colLabels=df_top50.columns,
loc='center',
bbox=[0,0,1,1])
plt.savefig('./df_BMI.png')
因果木で木構造の可視化
はい、ここでやっと本題っぽいところです。CausalTreeの手法でCATEの分け方を可視化します。といっても作成された決定木の構造を図示するだけです。この辺りもMicrosoftの参考コードに載っています。
from econml.cate_interpreter import SingleTreeCateInterpreter
intrp = SingleTreeCateInterpreter(max_depth=1)
intrp.interpret(est, X)
# 木構造の情報を出力
intrp.export_graphviz(out_file='/cate_tree.dot') # パスは適宜変更してください。
# 木構造の可視化
# BMIが5.705以下かどうかで分けられている。
intrp.plot()
plt.show()
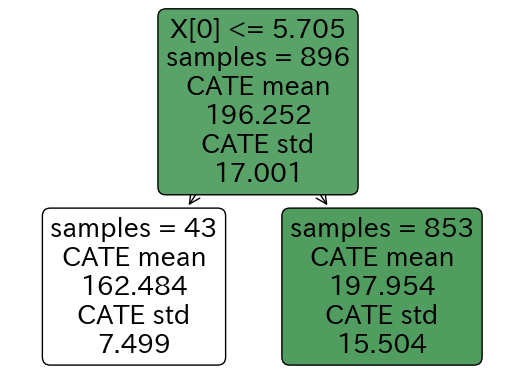
どのような基準で木を分けていて、それぞれの葉ノードのサンプル数、平均のCATEなどが記載されています。Google Colabratoryだとなぜか一発でこの図が可視化されない時があるので、しつこく「%matplotlib inline」と「plt.show()」を繰り返してみてください。
上記の二つがどちらもないと多分上手くいきません。
shapによる解釈
参考:https://recruit.cct-inc.co.jp/tecblog/machine-learning/shap/
続いて、EconMLの各モデルには、shap値を出すメソッドも用意されているので、shapでも分析結果の解釈を行ってみました。
shap_values = est.shap_values(X)
shap_values
defaultdict(dict,
{'Y0': {'T0': .values =
array([[ 1.00366147e+02],
[ 2.55709026e+01],
[-2.92744567e+01],
[-7.46359235e+02],
[ 1.06015945e+02],
[-1.23988548e+02],
[ 2.61077434e+02],
[-2.55348903e+02],
[ 4.37343130e+02],
[-2.00393124e+01],
・
・
・
以下略
import shap
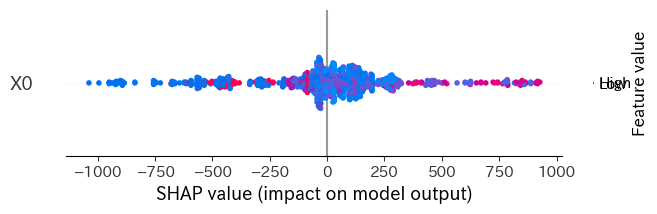
# effect heterogeneity feature importances with summary plot
shap.summary_plot(shap_values['Y0']['T0'])
# かなりバラバラなので、BMIが高いほど処置効果が高い、低いなどのことはこの図からは言えない。
モデルによって['T0']になったり['T0_1']になったりするので、その辺りは実際のshap_valuesを確認して調整してください。
モデルの解釈については上記の参考記事が参考になります。
shap.initjs()
# explain the heterogeneity of the effect of any single sample
shap.force_plot(shap_values['Y0']['T0'][0])
# BMIが14.08だと処置効果が高くなる(100(赤い部分の幅)程度の寄与)
以上のような工程を繰り返して、「ステータスごとの、伝説かどうかが捕まえやすさに与える影響」、「重さごとの、複合タイプかどうかがステータスに与える影響」、「重さごとの、複合タイプかどうかが進化時のステータスの伸びに与える影響」などについても分析してみましたが、後の工程はほぼ同じなので割愛させていただきます。一応、作成したコードをこちらで共有させていただきます。ポケモンやる人にも割と興味深い内容だと思うので、よければ見てみてください。御指摘等ございましたら、コメントをよろしくお願いいたします。
最後に、CausalForestモデルで複数のXのfeature_importanceを調べたり、LinearDMLというモデルで交互作用項について調べたりなんかもできるので、簡単に概要を載せさせていただきます。
# データを学習用と検証用で分ける
from sklearn.model_selection import train_test_split
train, test = train_test_split(df, train_size=0.7)
print(train.shape, test.shape)
features = ['高さ', '重さ', 'BMI', 'HP', 'こうげき', 'ぼうぎょ', 'とくこう', 'とくぼう', 'すばやさ', '捕まえやすさ']
train_X = train[features].values # 説明変数
W = None # 各サンプルを調整する重み。今回はなしとする。
train_T = train[['複合タイプ']].values # 処置変数
train_Y = train['伝説'].values # 目的変数
from econml.grf import CausalForest
model = CausalForest(
n_estimators=100, # 木の数
criterion='mse', # 評価指標
max_depth=10, # 木の最大の深さ
min_samples_split=10, # ノードを分割するのに必要なサンプル数
min_samples_leaf=5 # 各葉ノードに必要なサンプル数
)
model.fit(train_X, train_T, train_Y, sample_weight=W)
# feature_importance
model.feature_importances_
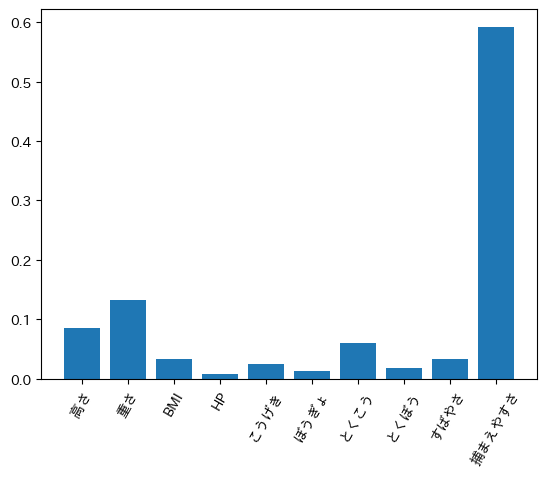
# 各説明変数の変数重要度をグラフで図示
plt.bar(np.arange(len(features)), model.feature_importances_, tick_label=features)
plt.xticks(rotation=60)
# 捕まえやすさが一番伝説たらしめている要因として強いことが分かる。
from econml.dml import LinearDML
from sklearn.preprocessing import PolynomialFeatures
est = LinearDML(model_y=RandomForestRegressor(), # Any ML model for E[Y|X,W]
model_t=RandomForestRegressor(), # Any ML model for E[T|X,W]
# sklearnのPolynomialFeaturesで、2次までの交互作用項や累乗項を作成する
featurizer=PolynomialFeatures(degree=2, include_bias=False)) # any featurizer for
est.fit(Y, T, X=X, W=W)
est.summary()
# LinearDMLの場合
# 有意水準95%でp値が有意なのはX4(こうげき)以外の単変数、x0^2, X0 X2, X0 X3, X0 X4, X0 X5, X0 X6, X0 X8, X1 X3, X1 X9, X2 X9, X3 X6, X3 X7, X3 X9, X6 X9, X7 X9, X9^2
# x0^2 : 高さの二乗 係数 -0.008
# X0 X2: 高さ×BMI 係数 0.001
# X0 X3: 高さ×HP 係数 0.003
# X0 X4: 高さ×こうげき 係数 0.0
# X0 X5: 高さ×ぼうぎょ 係数 0.003
# X0 X6: 高さ×とくこう 係数 0.002
# X0 X8: 高さ×すばやさ 係数 0.003
# X1 X3: 重さ×HP 係数 0.0
# X1 X9: 重さ×捕まえやすさ 係数 0.0
# X2 X9: BMI×捕まえやすさ 係数 0.0
# X3 X6: HP×とくこう 係数 0.0
# X3 X7: HP×とくぼう 係数 0.0
# X3 X9: HP×捕まえやすさ 係数 0.0
# X6 X9: とくこう×捕まえやすさ 係数 0.0
# X7 X9: とくぼう×捕まえやすさ 係数 0.0
# X9^2 : 捕まえやすさの二乗 係数 0.0
Coefficient Results
point_estimate stderr zstat pvalue ci_lower ci_upper
X0 -0.763 0.0 -196474.817 0.0 -0.763 -0.763
X1 0.008 0.0 48.359 0.0 0.007 0.008
X2 -0.007 0.0 -53.918 0.0 -0.007 -0.007
X3 -0.01 0.0 -77.765 0.0 -0.01 -0.01
X4 0.0 0.0 1.156 0.248 -0.0 0.001
X5 0.002 0.0 11.097 0.0 0.002 0.003
X6 0.003 0.0 16.422 0.0 0.003 0.004
X7 -0.004 0.0 -23.618 0.0 -0.004 -0.003
X8 -0.002 0.0 -20.138 0.0 -0.002 -0.002
X9 0.003 0.0 8.365 0.0 0.002 0.003
X0^2 -0.008 0.0 -179.041 0.0 -0.008 -0.008
X0 X1 -0.0 0.0 -1.257 0.209 -0.001 0.0
X0 X2 0.001 0.0 4.919 0.0 0.0 0.001
X0 X3 0.003 0.0 7.955 0.0 0.003 0.004
X0 X4 -0.0 0.0 -3.075 0.002 -0.001 -0.0
X0 X5 0.003 0.0 8.32 0.0 0.002 0.003
X0 X6 0.002 0.0 8.12 0.0 0.002 0.002
X0 X7 0.0 0.0 1.254 0.21 -0.0 0.001
X0 X8 0.003 0.0 24.424 0.0 0.003 0.003
X0 X9 0.0 0.0 0.643 0.52 -0.001 0.001
X1^2 0.0 0.0 1.187 0.235 -0.0 0.0
X1 X2 -0.0 0.0 -1.205 0.228 -0.0 0.0
X1 X3 -0.0 0.0 -3.869 0.0 -0.0 -0.0
X1 X4 -0.0 0.0 -0.124 0.901 -0.0 0.0
X1 X5 -0.0 0.0 -1.144 0.253 -0.0 0.0
X1 X6 0.0 0.0 0.177 0.86 -0.0 0.0
X1 X7 -0.0 0.0 -2.752 0.006 -0.0 -0.0
X1 X8 -0.0 0.0 -1.634 0.102 -0.0 0.0
X1 X9 -0.0 0.0 -2.643 0.008 -0.0 -0.0
X2^2 0.0 0.0 1.401 0.161 -0.0 0.0
X2 X3 0.0 0.0 1.382 0.167 -0.0 0.0
X2 X4 -0.0 0.0 -0.187 0.851 -0.0 0.0
X2 X5 0.0 0.0 1.528 0.126 -0.0 0.0
X2 X6 0.0 0.0 0.958 0.338 -0.0 0.0
X2 X7 0.0 0.0 0.76 0.448 -0.0 0.0
X2 X8 0.0 0.0 1.12 0.263 -0.0 0.0
X2 X9 0.0 0.0 3.053 0.002 0.0 0.0
X3^2 -0.0 0.0 -0.109 0.913 -0.0 0.0
X3 X4 0.0 0.0 0.864 0.388 -0.0 0.0
X3 X5 0.0 0.0 0.429 0.668 -0.0 0.0
X3 X6 -0.0 0.0 -2.131 0.033 -0.0 -0.0
X3 X7 0.0 0.0 2.751 0.006 0.0 0.0
X3 X8 -0.0 0.0 -0.423 0.673 -0.0 0.0
X3 X9 0.0 0.0 2.175 0.03 0.0 0.0
X4^2 0.0 0.0 0.629 0.529 -0.0 0.0
X4 X5 -0.0 0.0 -0.903 0.366 -0.0 0.0
X4 X6 0.0 0.0 1.006 0.314 -0.0 0.0
X4 X7 -0.0 0.0 -1.631 0.103 -0.0 0.0
X4 X8 -0.0 0.0 -0.715 0.475 -0.0 0.0
X4 X9 0.0 0.0 0.708 0.479 -0.0 0.0
X5^2 -0.0 0.0 -1.343 0.179 -0.0 0.0
X5 X6 0.0 0.0 0.113 0.91 -0.0 0.0
X5 X7 -0.0 0.0 -0.065 0.948 -0.0 0.0
X5 X8 -0.0 0.0 -0.015 0.988 -0.0 0.0
X5 X9 -0.0 0.0 -0.894 0.372 -0.0 0.0
X6^2 -0.0 0.0 -0.663 0.507 -0.0 0.0
X6 X7 0.0 0.0 0.464 0.642 -0.0 0.0
X6 X8 -0.0 0.0 -0.513 0.608 -0.0 0.0
X6 X9 -0.0 0.0 -2.719 0.007 -0.0 -0.0
X7^2 -0.0 0.0 -0.956 0.339 -0.0 0.0
X7 X8 0.0 0.0 0.71 0.478 -0.0 0.0
X7 X9 0.0 0.0 2.956 0.003 0.0 0.0
X8^2 0.0 0.0 0.186 0.853 -0.0 0.0
X8 X9 -0.0 0.0 -0.169 0.866 -0.0 0.0
X9^2 -0.0 0.0 -5.196 0.0 -0.0 -0.0
CATE Intercept Results
point_estimate stderr zstat pvalue ci_lower ci_upper
cate_intercept 0.559 0.0 115311.542 0.0 0.559 0.559
A linear parametric conditional average treatment effect (CATE) model was fitted:
$Y = \Theta(X)\cdot T + g(X, W) + \epsilon$
where for every outcome $i$ and treatment $j$ the CATE $\Theta_{ij}(X)$ has the form:
$\Theta_{ij}(X) = \phi(X)' coef_{ij} + cate\_intercept_{ij}$
where $\phi(X)$ is the output of the `featurizer`
Coefficient Results table portrays the $coef_{ij}$ parameter vector for each outcome $i$ and treatment $j$. Intercept Results table portrays the $cate\_intercept_{ij}$ parameter.
参考
CATE, CausalTreeなどについて
https://note.com/dd_techblog/n/nd30f5a7a5034
https://saltcooky.hatenablog.com/entry/2020/01/17/021448
https://cintelligence.co.jp/2020/06/12/blog-causal-inference-5/
EconMLについて
公式ドキュメント
https://econml.azurewebsites.net/index.html
MicroSoftResearchの研究グループによる、参考コード付きのチュートリアル
https://causal-machine-learning.github.io/kdd2021-tutorial/
EconMLについて解説している日本語記事
https://usaito.hatenablog.com/entry/2019/04/07/205756
https://usaito.hatenablog.com/entry/2019/04/07/205756
おわりに
いやーなんかめちゃくちゃ長大な記事になってしまいましたし、普通に疲れました。でも書いている途中で新たな記事や動画を見つけたりもして、まだまだ色々勉強してみようと思える分野でした。
徐々に理解が深まるにつれ、分かることが増えていって世界が広がるのがなんだか楽しいなと思いました。
今回自分が学んでいて難しいと感じた部分やつまずいた部分も踏まえて、計量経済学などにバックグラウンドがない方にもなるべくとっつきやすいように書いたつもりですが、大半がポケモンの話になってしまっている気もします(笑)。
今度はグラフニューラルネットワーク辺りについても勉強してみたいです。
またいつかポケモンネタで記事を書くかもしれません。
それではベストウイッシュ。良いデータサイエンスライフを。