次々と新しい技術が登場するITの世界。それを追いかけるだけでも時間が足りないのに機械学習もとなると大変です。詳しく調べる前に概略を知りたい。そんな機械学習の暗闇にスポットライトをあてたい。
今回のテーマは「主成分分析で多重共線性の問題を回避する」です。
多重共線性の問題については以前の記事↓を参照ください。
多重共線性
https://qiita.com/ydclab_P002/items/95d34564faf6e28d3c3f
主成分分析
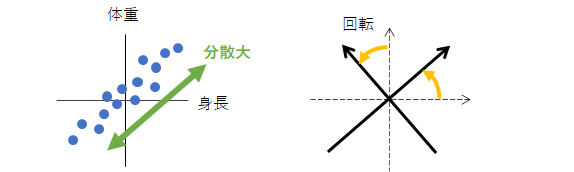
身長と体重から腹囲を予測したいが、身長と体重には強い相関があるとします(下左図)。
新たな軸を作成し分散が最大となるように回転させます(下右図)。
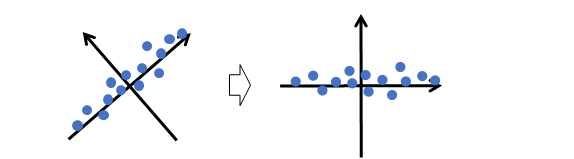
新しい軸の成分(下図)は、身長と体重に共通する成分(横軸)とそれ以外の成分(縦軸)です。
このとき縦軸の成分を誤差とみなして切り捨てると、主要な成分(横軸)を残しつつ2つの変数を1つに削減できます(次図)。
この横軸の成分にあえて命名するとすれば「体の大きさ」を表す潜在的な変数です。
これがデータから主成分を抽出する主成分分析(PCA, Principal Component Analysis)の概略です。なお、軸を減らすことを次元削減や次元圧縮などといいます。
主成分回帰 PCR で多重共線性の問題を回避
入力変数間に強い相関関係が存在する場合、誤差の拡大効果によって回帰係数の推定結果を信頼できなくなるのが多重共線性の問題です。
次元削減で誤差成分を取り除き、抽出した主成分を用いて線形回帰モデルを構築すれば、多重共線性の問題を回避できます。これを主成分回帰(PCR, Principal Component Regression)といいます。このとき次元削減せずに全ての成分を用いると多重共線性の問題を回避できないので注意してください。
scikit-learn(Python)を用いて PCR を試します。
訓練データ
| 腹囲 $y$ |
身長 $x_1$ |
体重 $x_2$ |
|---|---|---|
| 0.99 | 1 | 1.01 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
このまま線形回帰モデルを適用すると体重 $x_2$ が増えると腹囲 $y$ が減るという期待を裏切る回帰係数が得られます。
import numpy as np
from sklearn.linear_model import LinearRegression
y = np.array([[0.99], [2], [3]])
X = np.array([[1, 1.01], [2, 2], [3, 3]])
lr = LinearRegression()
lr.fit(X, y)
# 回帰係数
lr.coef_
実行結果(回帰係数)
array([[ 2., -1.]])
テストデータ(身長、体重)=(1, 2)を予測させると腹囲はほぼゼロとなり、期待を裏切る結果が得られます。
# テストデータ
X_test = np.array([[1, 2]])
lr.predict(X_test)
実行結果(テストデータの予測結果)
array([[-1.99840144e-15]])
次は PCR を試します。
説明変数を1次元に削減します(n_components=1 を指定)。
from sklearn.decomposition import PCA
# 1次元に削減
pca = PCA(n_components=1)
pca.fit(X)
# 主成分
Z = pca.transform(X)
Z
実行結果(主成分)
array([[-1.4095069 ],
[-0.00235111],
[ 1.41185802]])
次元削減した主成分を用いて線形回帰モデルを構築し、テストデータを予測します。
pcr = LinearRegression()
pcr.fit(Z, y)
pcr.predict(pca.transform(X_test))
実行結果(テストデータの予測結果)
array([[1.48997711]])
腹囲はおよそ 1.5 と予測されました。
多重共線性の問題を回避できたようです。
PLS
PCR は目的変数と無関係に主成分を決定します。このため主成分が予測に寄与するとは限りません。その欠点を補うのが PLS(Partial Least Squares Regression)です。PLS は、目的変数との相関が最大となるように主成分を決定します。詳しくは、参考文献をご覧ください。