はじめに
本稿では、PythonとGoogleのortoolsを用いて最適化を学んでいきます。
私のようなプログラマーが理解しやすいよう、用語も意図的にそちらへ寄せています。
同様にプログラムコードもなるべくそちらへ寄せています。
第一回の今回はナンプレをCP-SATで解きます。
環境
ローカル環境構築はそれだけで一本の記事になってしまいます。
本稿の本題ではないため、GoogleのColaboratoryを使用することで、
ローカル環境への構築などはすっ飛ばすことにします。
記事投稿段階では
Python3.7
ortools9.3
を使用しています。
1.ortoolsインストール
Colab上で以下を実行します。
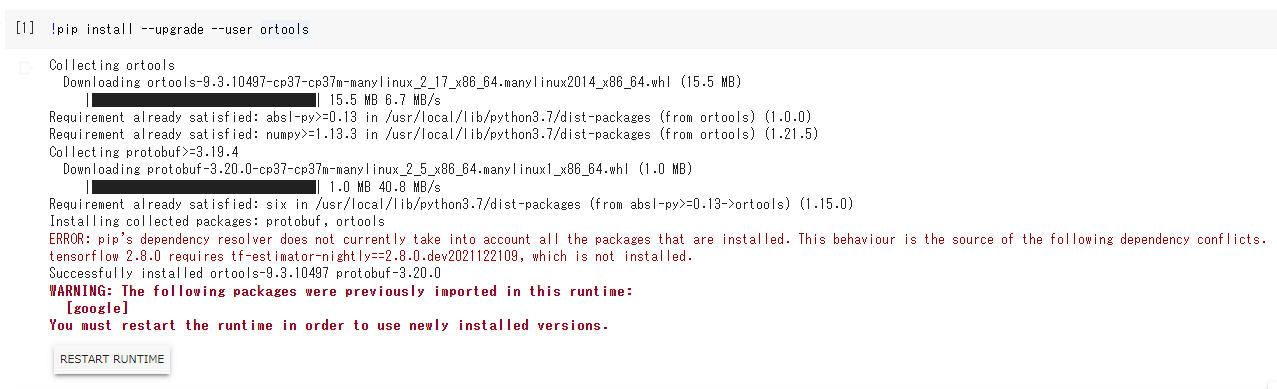
!pip install --upgrade --user ortools
※tensorflow2.8の依存関係でエラーが出ますが、本稿では問題とならないため無視します。
画面の指示通りRuntimeをRestartしておきましょう。
Colabでは、Runtimeの再起動が起こるとインストールパッケージは
失われます。このpipもColab上に記載しておいて必要に応じて
動かすと後々楽になります。
確認
今回はCP-SATソルバーを利用します。
importで確認。
from ortools.sat.python import cp_model
実行してエラーが出なければひとまずOK.
ナンプレ
ナンプレの基本ルールは以下になります。
ルール① 9x9の盤上に、1~9の数字を配置します
ルール② 同一行内では1~9がそれぞれ一回ずつ登場します
ルール③ 同一列内でも1~9がそれぞれ一回ずつ登場します
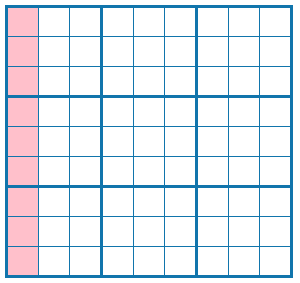
ルール④ 3x3のブロック内でも1~9がそれぞれ一回ずつ登場します
考え方
最適化ではまずソルバーに値を探らせる領域を考えます。
この領域の取り方で制約のつけ方も変わってきますし、
それによって探査に要する時間は大きく変わります。
さて、ナンプレの場合ですが。
ナンプレでは問題盤上は9x9のマス目になります。
このマスそれぞれが1~9の値を取ることとなります。
ortoolsのCP-SATソルバーでは、bool型以外にint型の利用も可能になっているため、
int型でやる方法もありますが、やはりboolで処理が可能であればその方がパフォーマンスが
出せるシーンが多いため、本稿ではbool変数を用います。
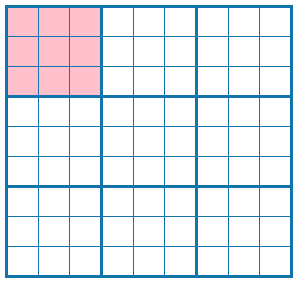
9x9それぞれに対して、1~9を意味する9要素のboolという形で
9x9x9のbool配列でデータを保持するイメージになります。

奥行方向は、1~9を意味します。
行、列方向は問題平面と捉えればOKです。
この用意した領域に、1/0のboolを割り当てて探査が行われます。
では実際に領域を準備してみます。
from ortools.sat.python import cp_model
# モデルインスタンス生成
model = cp_model.CpModel();
# 領域作成
ans = {}
for i in range(9): # 行方向
for j in range(9): # 列方向
for k in range(9): # 奥行方向(1~9)
ans[(i, j, k)] = model.NewBoolVar("ans_%i_%i_%i" %(i, j, k))
制約(ルールの適用)
ルール①
9x9の盤上に、1~9の数字を配置します
読み替えると、1マスには1~9の何れかの数字が必ず入ります。
つまり奥行方向の1本に対しては何れかのマスのみがtrue(1)となります。

bool変数は1/0の変数ですので、合計が1となる制約をかけることでこれを実現します。
# 制約(k方向にどれか一個1)(答えの1マスには一つの数値しか存在できない)
for i in range(9):
for j in range(9):
model.Add(sum(ans[(i,j,k)] for k in range(9))==1)
ルール②
同一行内では1~9がそれぞれ一回ずつ登場します
同一行内の、1を意味する部分では何れか一つだけがtrue(1)ということですね。
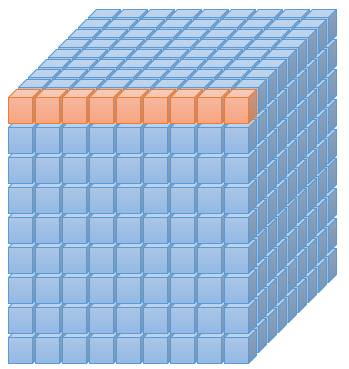
# 制約(i方向にどれか一個1)(答えの1行には各数値は一つずつしか存在できない)
for j in range(9):
for k in range(9):
model.Add(sum(ans[(i, j, k)] for i in range(9))==1)
ルール③
同一列内でも1~9がそれぞれ一回ずつ登場します
列方向も同様です。
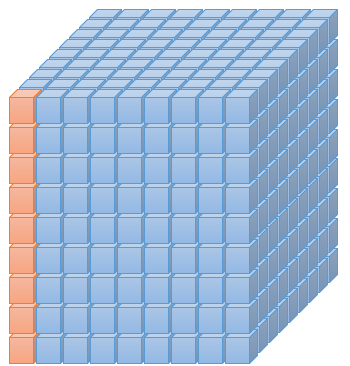
# 制約(j方向にどれか一個1)(答えの1列には各数値は一つずつしか存在できない)
for i in range(9):
for k in range(9):
model.Add(sum(ans[(i, j, k)] for j in range(9))==1)
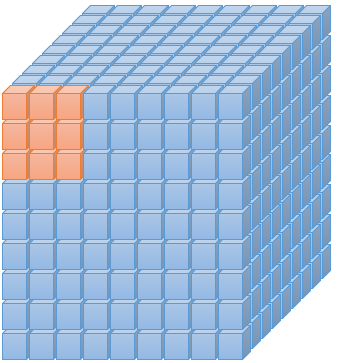
ルール④
3x3のブロック内でも1~9がそれぞれ一回ずつ登場します
これも同様です。
(用意した配列の形上、プログラムコード上は少しめんどくさい・・・)
# 3x3に区切られたマス内でも各数字は一つしか存在できない
for k in range(9):
for i3 in range(3):
model.Add(sum(ans[(i3*3+i,j,k)] for i in range(3) for j in range(0,3))==1)
model.Add(sum(ans[(i3*3+i,j,k)] for i in range(3) for j in range(3,6))==1)
model.Add(sum(ans[(i3*3+i,j,k)] for i in range(3) for j in range(6,9))==1)
動かしてみる
さて、今の段階では変数が用意され、ナンプレルールに従った制約が定義されただけです。
問題入力はされていません。
人間だと何から取り掛かるか困ってしまいますが、ルールに従えば良いだけと捉えると
これには複数の答えがあるだけという理解もできます。
試しに動かしてみましょう。
solver = cp_model.CpSolver()
status = solver.Solve(model)
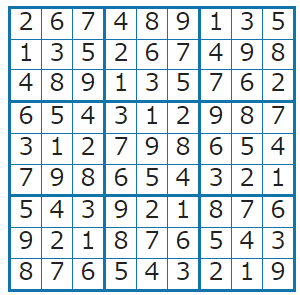
ルールに従った結果が一つ得られました。
実行環境によってはこれとは異なる結果になります
同様に動かす度に異なる結果が得られる場合もあります
ここで得られた結果の一番左上は2でした。
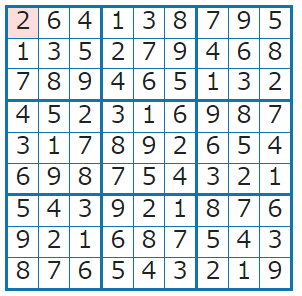
今度は問題として一番左上に2が指定されただけの問題を設定してみます。
問題入力を2次元の配列で行うこととし、0は未定マスとして定義します。
prob = [
[2,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
]
solverへ制約を適用します。
for i in range(9):
for j in range(9):
if (prob[i][j] > 0):
for k in range(9):
if (k+1 == prob[i][j]):
model.Add(ans[i, j, k]==1)
else:
model.Add(ans[i,j,k]==0)
制約の適用があるため挙動が変わり、さきほどとは異なる結果が得られるかと思います。
環境に寄っては同じ結果となる場合もあります
実際に解いてみる
インターネットで見つかる問題を解いてみようかと思いましたが、
ナンプレの問題には著作権が存在する解釈もあります。
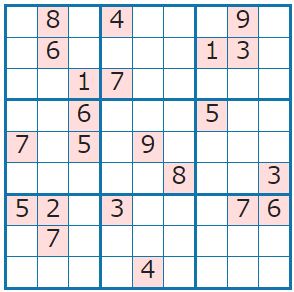
ということで、私が適当に作った問題で解いてみます。
解が一つでない可能性もありますがそこはご了承ください。
prob = [
[0,8,0,4,0,0,0,9,0],
[0,6,0,0,0,0,1,3,0],
[0,0,1,7,0,0,0,0,0],
[0,0,6,0,0,0,5,0,0],
[7,0,5,0,9,0,0,0,0],
[0,0,0,0,0,8,0,0,3],
[5,2,0,3,0,0,0,7,6],
[0,7,0,0,0,0,0,0,0],
[0,0,0,0,4,0,0,0,0],
]
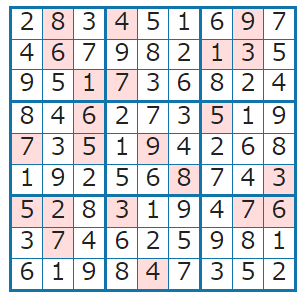
無事に解が見つかりました。
さいごに
今回はナンプレをortoolsのCP-SATで解いてみました。
今後もパズルに限らず色々なことを最適化で解いてみようと思っています。
おまけ
結果参照系は本稿の本題と異なるため本文中では割愛しました。
以下のような表示用関数を用意して結果を視覚化しています。
表示関数
from IPython.display import HTML
def make_table(ans_int_9x9, quest_int_9x9):
table_style = "<style>\
<!--\
table.numpre{\
border:#1175ac solid 3px;\
font-size:24px;\
border-collapse: collapse;\
}\
table.numpre tr{\
height: 30px;\
}\
table.numpre td{\
border:#1175ac solid 1px;\
width: 30px;\
padding: 0;\
text-align:center !important;\
background-color:white;\
}\
table.numpre td:nth-of-type(3),table.numpre td:nth-of-type(6){\
border-right:#1175ac solid 3px;\
}\
table.numpre tr:nth-of-type(3),table.numpre tr:nth-of-type(6){\
border-bottom:#1175ac solid 3px;\
}\
-->\
</style>"
ret = ""
for i in range(len(ans_int_9x9)):
ret += "<tr>"
for j in range(len(ans_int_9x9[i])):
bgcolor = ""
if (quest_int_9x9[i][j] > 0):
bgcolor = "style=\"background-color:#fdd;\""
if ans_int_9x9[i][j] == 0:
ret += "<td "+bgcolor+">" + "</td>"
else:
ret += "<td "+bgcolor+">" + str(ans_int_9x9[i][j]) + "</td>"
ret += "</tr>"
return table_style + "<table class=\"numpre\">" + ret + "</table>"
Solve実行後の結果参照
ans_int = [
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0],
]
if ((status == cp_model.OPTIMAL) or (status == cp_model.FEASIBLE)):
for i in range(9):
for j in range(9):
for k in range(9):
if (solver.Value(ans[(i,j,k)])):
ans_int[i][j]=k+1
break
else:
print("could not optimize")
output = make_table(ans_int, prob)
HTML(output)
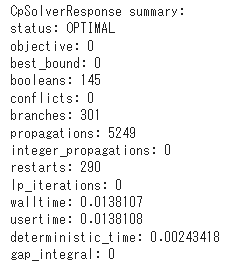
solver実行時のステータスも確認できます。
print(solver.ResponseStats())