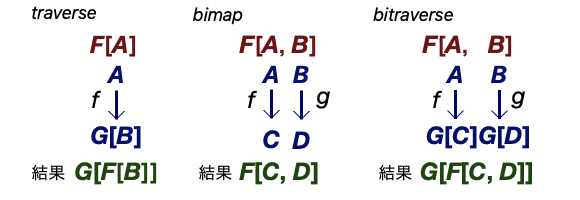Scala の関数型プログラミングライブラリ Cats でたまに見かける、ふだん余り使わないけど何か気になる型クラスを調べてみた。
はじめに
Cats でよく使う型クラスといえば、Monad、Monoid、Functor を筆頭に Applicative、Traverse あたりがメジャーどころだと思うけど、ソースやドキュメントを読んでいると、何となく目について興味をひかれるものの、実用上ふだんはスルーしてるクラスがたまにある。以前にもそんなマイナーな型クラスが気になって、Profunctor、 PartialOrder 、Distributive などについて記事を書いた。
今回もそうした趣旨の延長で、kernel、core、core/arrow の型クラスから 5つ、Group、Alternative、Bitraverse、Covariant、Category を選んで試してみたい。どういうところが気になるのかは個別に書いていく。
Group
ここが気になる
関数型プログラングをしていると、コレクションの畳み込みや、ログの集積などで、半群(Semigroup) や モノイド(Monoid) は結構よく使うけど、その先の群(Group)は全然使ったことがない。数学では群論として一大分野をなしていて、圏論でも群論からの例がよく使われる。Cats にもこれに対応する型クラス Group がちゃんとあるので、見るたびに気になる。
ざっくり解説
半群に単位元を付けてモノイドにして、さらに逆元を与えると群になる感じ。たとえば整数の足し算とか、正多角形の反転や回転とか、あとルービックキューブとかも群になる。
ここではシンプルにあみだくじを実装して、これが群の条件を満たすことを確認してみる。
サンプル
下記のように4ライン(縦線)の Amida クラスを実装した。隣り合うラインをつなげる横棒のリストを legsに持っている。
opaque type Amida = List[Int]
object Amida:
val Lines = 4
val Empty: Amida = List.empty[Int]
def apply(legs: List[Int]): Amida = legs
extension (self: Amida)
def combine(another: Amida): Amida = self ++ another
def inverse : Amida = self.reverse
def permutation: Vector[Int] = self.foldLeft((0 until Lines).toVector)(
(acc, l) => acc.updated(l, acc(l + 1)).updated(l + 1, acc(l)))
群の二項演算は combine、単位元は Empty、逆元は inverse として実装した。メソッド permutation は位置を 0 始まりであらわした置換、つまりあみだくじを辿った結果、どれがとこに行き着くかをあらわす数字の並びで、後述する Amida の等値性の判定にも用いている。
例として、たとえば下図のようなアミダなら、Amida(List(0, 2, 1))で、permutationは (1, 3, 0, 2)となる。
0 1 2 3
├─┤ │ │
│ │ ├─┤
│ ├─┤ │
これについて、下記のように Group インスタンスを定義すると、Amida が群として扱えるようになる。二項演算、単位元、逆元は、Amida の実装をそのまま使っている。
given Group[Amida] with
def inverse(a: Amida): Amida = a.inverse
def empty: Amida = Amida.Empty
def combine(x: Amida, y: Amida): Amida = x combine y
実際にこれが群の条件を満たすことを、以下のように Discipline を使って確かめられる。上述のとおり、等値性 Eq は permutation を比べている。
class GroupSpec extends DisciplineSuite:
import Gen.{ chooseNum, listOfN }
given Eq[Amida] = _.permutation == _.permutation
given Arbitrary[Amida] = Arbitrary {
for {
len <- chooseNum(0, 5)
legs <- listOfN(len, chooseNum(0, Lines - 2))
} yield Amida(legs)
}
checkAll("group of Amida", GroupTests[Amida].group)
実行すると下記のような出力と共にテスト成功し、Admidaが群の法則をみたしていることがわかる。

ドメイン駆動設計に Closure of Operation というプラクティスがあって、特に Value Object に関連して引数と結果が同じ型となる「閉じた演算」のことを指すが、代数的には半群、モノイドあたりに関わりが深い。特に、どの操作についても対応するやり直し- Undo 操作があると、それを逆元として群が成立する可能性がでてくる。
ドメインモデリングにおいても、このあたりの代数的構造を意識しておくと、Discipline などを用いた代数的なプロパティベーステストや形式的なモデル検査などができるようになるかもしれない。群を見たらそれが群なのだと気付けるくらいにはしておきたい。
Alternative
ここが気になる
Cats 公式の型クラスの図をみると、「ドキュメントも豊富で有名な型クラスなので最初に勉強すべき」として、Monad や Monoid などがハイライトされているが、Alternative だけは正直なじみがない。気になる。
ざっくり解説
Applicative から pure と ap、 MonoidK から empty と combineKを受け継いだ型クラスで、ドキュメントによるとパーズなどで優先順位つきの代替戦略を与えたり、Bifoldable と併用してコレクションの分割などに使えるらしい。
ここでは、代替の例として FizzBuzz を題材にして試行してみる。
サンプル
まず与えられた数nに対して、適当な基準で Some[A] かNone を返す trait Div を、下のように定義する。コンパニオンオブジェクトは、割る数と割り切れた場合の文字列から Div[String] を生成する apply と、常に与えられた整数を文字列化して返す Default を提供する。
trait Div[A] extends Function1[Int, Option[A]]:
def apply(n: Int): Option[A]
object Div:
def apply(m: Int, s: String): Div[String] = _.some.filter(_ % m == 0).as(s)
val Default: Div[String] = _.toString.some
Alternative[Div] インスタンスは以下のように書ける。
given Alternative[Div] with
def empty[A]: Div[A] = _ => None
def combineK[A](x: Div[A], y: Div[A]): Div[A] = in => x(in) orElse y(in)
def pure[A](x: A): Div[A] = _ => x.some
def ap[A, B](ff: Div[A => B])(fa: Div[A]): Div[B] = in => ff(in) <*> fa(in)
これを用いると、FizzBuzz が以下のように表現できる。
val fizzbuzz = Div(15, "FizzBuzz") <+> Div(3, "Fizz") <+> Div(5, "Buzz") <+> Default
(1 to 100).map(fizzbuzz.div).toList.sequence
以下のような普通の FizzBuzz の結果が得られる。
res0: Option[List[String]] = Some(List(1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz, 11, Fizz, 13, 14, FizzBuzz, 16, 17, Fizz, 19, Buzz, Fizz, 22, 23, Fizz, Buzz, 26, Fizz, 28, 29, FizzBuzz, 31, 32, Fizz, 34, Buzz, Fizz, 37, 38, Fizz, Buzz, 41, Fizz, 43, 44, FizzBuzz, 46, 47, Fizz, 49, Buzz, Fizz, 52, 53, Fizz, Buzz, 56, Fizz, 58, 59, FizzBuzz, 61, 62, Fizz, 64, Buzz, Fizz, 67, 68, Fizz, Buzz, 71, Fizz, 73, 74, FizzBuzz, 76, 77, Fizz, 79, Buzz, Fizz, 82, 83, Fizz, Buzz, 86, Fizz, 88, 89, FizzBuzz, 91, 92, Fizz, 94, Buzz, Fizz, 97, 98, Fizz, Buzz))
素朴なイメージではなんとなく手続き型ぽい FizzBuzz も、Alternative を使うと、関数型らしく合成 で表現できるようになった。
Bitraverse
気になるところ
Cats を使っていると Bimonad や Bifoldable など、bi がつくものをよくみかける。圏論の入門書などでも、双関手(Bifunctor)が出てくるが、結構基本的な概念らしく気になってしまう。その中でも、今回は Bitraverse をやってみる。
ざっくり解説
Bitraverse の基底クラスでもある Bifunctor 以下の型クラスは、タプルや Either のような A面と B面を持つ型の両面への操作を提供するかたちになる。特に Bitraverse.bitraverse は、Traverse.traverse と Bifunctor.bimap を合わせたようなもので、それぞれ下図のように図式化できる。
ここでは、タプルのコレクションを Bitraverse にしてみる。
サンプル
コレクションは Chain を使ってみた。Bitraverse[TupleChain] インスタンスは下のようになる。
type TupleChain[A, B] = Chain[(A, B)]
given Bitraverse[TupleChain] with
def bitraverse[G[_]: Applicative, A, B, C, D](
fab: TupleChain[A, B])(f: A => G[C], g: B => G[D]): G[TupleChain[C, D]] =
fab.map(_.bitraverse(f, g)).sequence
def bifoldLeft[A, B, C](fab: TupleChain[A, B], c: C)(f: (C, A) => C, g: (C, B) => C): C =
fab.foldLeft(c)((cc, d) => d.bifoldLeft(cc)(f, g))
def bifoldRight[A, B, C](fab: TupleChain[A, B], c: Eval[C])(
f: (A, Eval[C]) => Eval[C],
g: (B, Eval[C]) => Eval[C]
) = fab.foldRight(c)(_.bifoldRight(_)(f, g))
bitraverse の実装の中で Cats 提供の Bitraverse[Tuple2]を利用している。Bifoldable から継承した foldLeft と foldRight の実装は、Bitraverse[Tuple2] のインスタンスを参考にして、タプルのコレクションを縫うように畳み込んでみた。
以下のように使える。
val tc1: TupleChain[Char, Double] = Chain(('a', 0.1), ('b', 0.2), ('c', 0.3))
val tc2: TupleChain[Char, Double] = Chain(('a', 1.5), ('b', -2.5))
val maybePercent = (d: Double) => Option.when(d >= 0)(s"${d * 100}%")
tc1.bitraverse(_.toUpper.some, maybePercent)
// Option[TupleChain[Char,String]] = Some(Chain((A,10.0%), (B,20.0%), (C,30.0%)))
tc2.bitraverse(_.toUpper.some, maybePercent)
// Option[TupleChain[Char,String]] = None
tc1.bifoldLeft("")((s, n) => s + s"<$n", (s, n) => s + s",$n>, ")
// String = "<a,0.1>, <b,0.2>, <c,0.3>, "
tc1.bifoldRight(Eval.now(100.0))((a, c) => c.map(_ - (a-'a')), (b, c) => c.map(_ + b)).value
// Double = 97.6
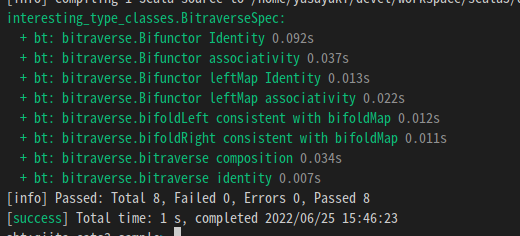
Discipline テストもうまくいく。
class BitraverseSpec extends DisciplineSuite:
import Gen.{ chooseNum, listOfN }
given Arbitrary[TupleChain[Int, Int]] = Arbitrary(
for {
len <- chooseNum(0, 3)
tuples <- listOfN(len, (chooseNum(0, 3), chooseNum(0, 3)).mapN((_, _)))
} yield Chain.fromSeq(tuples)
)
checkAll("bt", BitraverseTests[TupleChain].bitraverse[Option, Int, Int, Int, Int, Int, Int])
今回は練習がてら、あえて Bitraverse のインスタンスを自作してみたけど、こういうものだと頭の片隅に置いておけば、既成の Either や Tuple2 の Bifunctor 系型クラスでも結構使いどころが多いかもしれない。
Contravariant
気になるところ
圏論の入門書でもよくでてくる反変関手。Cats にもあって、『Scala with Cats 』でも紹介されているので、基本的な型クラスらしいが馴染みがない。やはり気になる。
ざっくり概要
『Scala with Cats』によれば、変換(transformation)をあらわすデータタイプ(Showなど)に、別の操作を prepend するものだという。下のように図式化してみた。
追加する変換操作の例としては、文字列のフォーマット、サブタイプからスーパタイプへのアップキャスト、メンバアクセスなどがある。
ここでは、ドキュメントにある Salary と Money のサンプルをちょっと変形したもので試行してみる。
サンプル
下記のような構成の給与明細を考えてみる。
Salary
├─ earnings: Earnings
│ └─ basic: Money
└─ deductions: Deductions
└─ tax: Money
そのままこんな風に表現する。
case class Money(amount: Int)
case class Earnings(basic: Money)
case class Deductions(tax: Money)
case class Salary(earnings: Earnings, deductions: Deductions)
val salary: Salary = Salary(Earnings(Money(100)), Deductions(Money(10)))
型A の値について何かを判別する Validate[A] があるとして、その Contravariant は下記のように定義できる。
trait Validate[A]:
def validate(a: A): Boolean
given Contravariant[Validate] with
def contramap[A, B](fa: Validate[A])(f: B => A) = b => fa validate f(b)
あとは元になる Validate[Money] に、型 A => Money の関数を組み合わせれば、Validate[A] が作れる。
val nonNegative: Validate[Money] = _.amount >= 0
val basic = (_: Earnings).basic
(nonNegative contramap basic) validate Earnings(Money(-100))
// res0: Boolean = false
val earningsAmount = (_: Salary).earnings.basic
val deductionsAmount = (_: Salary).deductions.tax
(nonNegative contramap earningsAmount) validate salary
(nonNegative contramap deductionsAmount) validate salary
// res1: Boolean = true
// res2: Boolean = true
val earnings = (_: Salary).earnings
(nonNegative contramap basic contramap earnings) validate salary
// res3: Boolean = true
今回は Contravariant 単独で調べてみたけど、Functor や Invariant と一緒に考えたり、あるいは ContravariantMonoidal と比較したりしてみると、また別の理解が得られるかもしれない。
Category
気になるところ
Cats といえば、その名称もロゴのデザインも圏論に由来するものなのだろうけど、Cats に含まれている Category という型クラスが語られているのをあまり見たことがない。名前的には圏論の主役のはずの概念なわけで、やはり何か気になる。
ざっくり解説
Cats の中では、cats.arrow パッケージの中で Compose とArrow の間に置かれていて、基本的な概念というより、どちらかというと Arrow を導入するための中間的な位置づけにみえる。ただし 恒等射 や 射の合成 など圏の要素を提供していて、実装に際しても圏の法則を満たすことが求められる。
素振りの材料としては対象より射に何を選ぶかで変わりそうだけど、あまり簡単すぎても(Function1とか)面白くないので Writer に向かうクライスリ射としてみた。
サンプル
Writer のログには Chain[String] をもたせた上で、可読性のために適当にエイリアスを定義した。
type ChainWriter[T] = Writer[Chain[String], T]
type KWriter[A, B] = Kleisli[ChainWriter, A, B]
また型 A => Bの関数を KWriter[A, B] にリフトする関数 lift を定義し、これを用いて以下のような具体的な射を用意しておく。
def lift[A, B](f: A => B) =
Kleisli[ChainWriter, A, B](a => Chain(s"$a").tell as f(a))
val d2s: KWriter[Double, String] = lift(s => s"$s%")
val s2n: KWriter[String, Int] = lift(_.length)
val n2d: KWriter[Int, Double] = lift(_ / 100.0)
Cats が提供する implicits によって、暗黙に Category[KWriter] が導出されるので、特に自前のインスタンスを定義する必要はないが、あえて書くとすれば下記のようなインスタンスになる。
given Category[KWriter] with
def id[A]: KWriter[A, A] = Kleisli[ChainWriter, A, A](_.writer(Chain.empty))
def compose[A, B, C](f: KWriter[B, C], g: KWriter[A, B]): KWriter[A, C] = f compose g
手動で圏の結合法則と単位法則を動かしてみると以下のようになる。Writer のログも想定通りに集積される。
// 結合法則
((n2d >>> d2s) >>> s2n) run 1234
(n2d >>> (d2s >>> s2n)) run 1234
// res0: ChainWriter[Int] = WriterT((Chain(1234, 12.34, 12.34%),6))
// res1: ChainWriter[Int] = WriterT((Chain(1234, 12.34, 12.34%),6))
// 単位法則
(id[Int] >>> n2d) run 1234
n2d run 1234
(n2d >>> id[Double]) run 1234
// res2: ChainWriter[Double] = WriterT((Chain(1234),12.34))
// res3: ChainWriter[Double] = WriterT((Chain(1234),12.34))
// res4: ChainWriter[Double] = WriterT((Chain(1234),12.34))
Arrow を使うときにも、Category のこうした機能や性質が継承されることを覚えておくといいかもしれない。
おわりに
Cats のコードやドキュメントを読んでると、まだまだ他にも、あまり使わないけど何か面白そうなマイナーなクラスがある。別の機会に、下記の観点でまたしらべてみたい。
-
effect、mtlに入ってるマイナー型クラス。 - Type class ではなく DataTypesのクラスたち。
(使った cats のバージョンは 1.5.0、scalacheckのバージョンは 1.13.5)