以前の記事で Cats のArrowを試してみた。cats.arrow パッケージの中で、Arrow は Strongを継承し、その Strong は 階層最上位の Profunctor を継承していた。
このProfunctorのdimapがちょっと面白いので、Cats のKleisli、Monocle の Lens 、マクロなどを併用してコードを書いてみた。
動くコード: note.worksheet.sc, Name.scala
依存ライブラリ等
- Scala 3.1.3
- cats 2.8.0
- monocle 3.1.0
Profunctor の dimap
Profunctorにはdimap、lmap、rmapがあるが、lmapとrmapはdimapを使って実装されているので、Profunctorのコアな部分はdimapになる。この記事ではdimapに着目する。
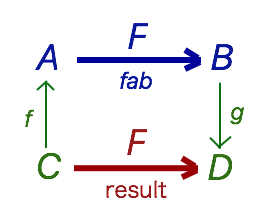
dimapの型は以下のようになる。
def dimap(fab: F[A, B])(f: C => A)(g: B => D): F[C, D]
絵にすると下図のようになる。
抽象的にいえばProfunctorは $C^{op}\times C\rightarrow C$と書け(Milewski7.2)、結果側の対象$C$から入力側の$A$に向かう、逆向きの矢印$f$が、双対圏 $C^{op}$に対応している。ちなみに $f$ も $g$ 同様に下向きにしたものがBifunctorのbimapで $C\times C\rightarrow C$ と表現できる(Milewski7.1)。(bimapの文字 b を左右逆にするとdimapになって意味も逆になるのが面白い。)
シンプルな例
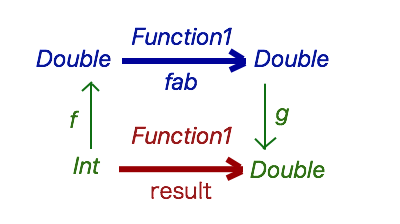
dimap の apiドキュメントに、以下のようなシンプルなコード例が載っている。
val fab: Double => Double = x => x + 0.3
val f: Int => Double = x => x.toDouble / 2
val g: Double => Double = x => x * 3
val h = Profunctor[Function1].dimap(fab)(f)(g)
h(3) //res0: Double = 5.4
Profunctor[Function1].dimap(fab)(f)(g)の部分は、cats.syntax.profunctor._ の構文をつかうとfab.dimap(f)(g)のように書ける。以降、この profunctor 構文をつかう。
これも上のように絵にしてみると以下のようになる。
アクセッサへの応用
上の数値型の計算より少しだけリアルな例題に応用してみる。
-
Person型とName型がある -
Person型はName型のnameフィールドを持つ。 -
Name型には「小文字アルファベット1文字以上」という制約がある1。
opaque type Name <: String = String // 別ファイルにてマクロと一緒に定義
case class Person(name: Name)
val p1 = Person(Name.from("test"))
val p2 = Person(Name.from("testfoo"))
※ Name の実装
object Name:
opaque type Name <: String = String
def apply(s: String): Either[String, Name] =
if s.matches("[a-z]+") then s.asRight else "error".asLeft
inline def from(inline s: String): Name = ${ fromImpl('s) }
private def fromImpl(s: Expr[String])(using Quotes): Expr[Name] =
import quotes.reflect.*
s.asTerm match
case Inlined(_, _, Literal(StringConstant(str))) =>
Name(str).fold(report.errorAndAbort, _ => s)
case _ => report.errorAndAbort("not constant")
このPerson#nameフィールドがプレフィックス 'test' で始まっていたら、それを削除するという関数を書きたい。
ただし、もし値が 'test' なら、これを取り除いた結果は空文字列になるので、Name型の制約が満たされず関数の結果は失敗となる。これを以下のようにErrorOr[Name]と表すことにする。
type ErrorOr[A] = Either[String, A]
普通の関数として書けば Name => ErrorOr[Name] といった型になるが、ここでは ErrorOr まで含めて Profunctor[F[_,_]] の F に組み込んで、クライスリ射Kleisli[ErrorOr, Name, Name]で表すことにする。
dimapの結果となる最終的な射は、Kleisli[ErrorOr, Person, Person]といった型となる。
とりあえず、ここまで図式化すると下図のようになる。
これを Scala で書くと以下のようになる。
val stripTest: Kleisli[ErrorOr, Name, Name] =
Kleisli(name => Name(name.stripPrefix("test")))
val nameLens = GenLens[Person](_.name)
def dimapped(p: Person) =
stripTest.dimap(nameLens.get)(nameLens.replace(_)(p))
-
図のfab:
dimap対象のクライスリ射はstripTestで表した -
図のf:
Person#nameのアクセッサは、Monocle を使ってnameLensとした。Person→Nameの場合、nameLens.getとなる。 -
図のg: Name→Personは、Personインスタンスを指定して
nameLens.replace(_)(p)となる。 -
図のresult:
fabをfとgでdimapした結果をdimappedで表した。
以下のように実行できる。
def stripTestFromName(p: Person) = dimapped(p).run(p)
stripTestFromName(p1) //Left(error)
stripTestFromName(p2) //Right(Person(foo))
stripTestFromName(Person(Name.from("abc"))) //Right(Person(abc))
Kleisli、lens、マクロ を併用することで、図のシンメトリックなところがコードにも反映できた。
雑感等
-
cats.arrowパッケージの階層最上位にあるのでもわかるようにProfunctorは抽象度が高く、Functorのmapや、Contravariantのcontramapも、Profunctorインスタンスがあればrmapやlmapで表現できる。 -
lmap、rmapそのものは、dimapの片側の $f$または $g$をidentityにすることで得られる。Cats のソースにもこの辺りが反映されていて面白い。 -
逆に
FunctorとContravariantがあればProfunctor#dimapを実装することもできるらしい(Milewski7.2: 00:46ごろ)。 -
あと圏論関連の講義で、双対で説明できるものは解説が省略されることが多いけど、独習する場合、やっぱり「余〜」、「Co〜」、「Contra〜」も図やコードを書いてみると、もとの概念の理解の助けにもなる気がする。
Cokleisliとか、Comonad、Coflatmapあたりも後で見ておきたい。
参考
- Youtube動画: Category Theory 7.2: Monoidal Categories, Functoriality of ADTs, Profunctors
- apidoc: cats/arrow/Profunctor.html#dimap
-
もともと refined を使っていたが、Scala 3 が未対応なので macro でベタ書きした(2022-08-09) ↩