はじめに
極値統計学については、Qiitaには極値統計学に軽く触れてみるや正規分布の最大値、最小値の分布といった素晴らしい記事がすでにアップされており、
Zennにも記事がアップされているので、こちらも参照いただいたほうが良いです。
「100年に一度」と極値統計学
よくマスコミや政府が使う「100年に一度の大雨」という表現、最近この表現が使われすぎていてやや陳腐化しているきらいがあります。
あまりにも頻繁に聞くものですから、「100年に一度なんて言って大したことないじゃないか、不安を煽りたいだけないんじゃないか?」と思ってしまいがち。
でも良く考えてみると、「この雨は100年に一度の大雨なんです!」というのは何を根拠に言っているのでしょう?
実は、このことは極値統計学によって出しています!
他には、腐食材と石油タンク底板の残存寿命の推定や、市場収益のモデル化、陸上競技においてどこまで人類は記録を伸ばせるか?という抽象的な問に対しても極値統計学は一定の解をもたらしています
(これによると100 m走は9秒29まで短縮可能らしい)。
なぜこのようなことができるのかというと、極値統計学とは最大値や最小値が得られる確率を求めるための手法だからです。
この記事では、極値統計学の簡単な理論と、アメダスのデータを用いた「100年に一度の降水量」の推定を行おうと思います。
極値分布
「最大値や最小値が得られる確率」と言われても具体的にはどういうものなのかわからないので、少し実験してみましょう。
手元にサイコロがあるとします。これらの出る目は同様に確からしく(つまり離散一様分布)、サイコロを3回降ったときの最大値を記録するという操作を2000回行ったとします。
ここで、どの目が最も最大値として記録されていそうだろうか? という問いを立てます。
平均であれば3.5になりますが、最大値が6になる確率は非常に高そうです。逆に、おそらく最大値が1となる確率は非常に低いでしょう。
実際にjuliaで書いてみると、
using Plots
using Distributions
using StatsBase
using StatsPlots
sample_max = zeros(Int, 6)
anim = Animation()
for i in 1:2000
max = maximum(sample(1:6, 3, replace=true))
sample_max[max] += 1
plt = bar(sample_max ./ i, xlims=(0.5, 6.5), ylims=(0, 0.5), label="", title = "Uniform dist: $i")
frame(anim, plt)
end
@time gif(anim, "maximum_Uniform.gif", fps = 20)
最大値が6になる確率は実際に高いようです、およそ0.4ぐらい。
しかも、なにかの分布に収束していそうな雰囲気があります。
これは偶然でしょうか?他の分布から得られた場合ではどうだろう、ということで正規分布から3回データをとり、その最大値を取るとしましょう。
anim = Animation()
sample_max = []
for i in 1:2000
push!(sample_max, maximum(rand(Normal(0, 1), 3)))
plt = histogram(sample_max, normalize=:probability,bin = -2:0.25:5,title = "Normal dist: $i")
frame(anim, plt)
end
@time gif(anim, "maximum_Normal.gif", fps = 20)
正規分布のような雰囲気がするが、やはり収束していそう。
指数分布やコーシー分布でも同様に描いてみます。
julia言語なら、randの中身を少し変えるだけで良いので便利。
anim = Animation()
sample_max = []
for i in 1:2000
push!(sample_max, maximum(rand(Exponential(), 3)))
plt = histogram(sample_max, normalize=:probability,bin = 0:10, title = "Exponential dist: $i")
frame(anim, plt)
end
@time gif(anim, "maximum_Exponential.gif", fps = 20)
anim = Animation()
sample_max = []
for i in 1:2000
push!(sample_max, maximum(rand(Cauchy(10), 3)))
plt = histogram(sample_max, normalize=:probability, title = "Cauchy dist: $i")
frame(anim, plt)
end
@time gif(anim, "maximum_Cauchy.gif", fps = 20)
また正規分布由来の分布とは異なる収束の仕方をしていますね。色々趣があって面白い!
このように、$\{X_i\}_{i=1}^{n}, n = 1,2,3, ...$で考えられる確率変数列の極値
(今回の場合は最大値、すなわち $ Z_{n} = max(X_1, X_2, ... , X_n)$)を考えるとその分布はどの様になるのか?ということを考える学問が極値統計学です。
このように分布が収束する場合、この分布を極値分布と呼びます。
端的に言えば「ある確率分布にしたがう独立な$N$個のサンプルがあったときに、そのサンプルの極値 (最大値や最小値など) の分布」のことを指しているということです。
アメダスのデータを使った「100年に一度の大雨」推定
極値分布は、理論的にはGumbel分布、Fréchet分布、そして負のWeibull分布の3種類のどれかになることがわかっています。
f(・)を確率密度関数、F(・)を累積分布関数とすると以下のような式で記述されます(この辺りは統計検定とか受けている人向けですかね?)。
-
Gumbel分布: $f(x; \alpha, \beta) = \frac{1}{\beta}\exp(-\exp(\frac{x-\alpha}{\beta})+\frac{x-\alpha}{\beta}), F(x;α,β)=\exp(−\exp(-\frac{x−\alpha}{\beta}))$
(もとの分布が指数分布や正規分布でこの分布に収束) -
Fréchet 分布: $f(x; \alpha) = \alpha x^{-\alpha-1}\exp(-x^{-\alpha}), F(x; \alpha) = \exp(-x^{-\alpha})$
(もとの分布がコーシー分布だとこの分布に収束) -
負のWeibull 分布: $f(x; \alpha, \beta) =\frac{\alpha} {\beta^\alpha}x^{\alpha-1}\exp(-(\frac{x}{\beta})^\alpha), F(x;\alpha, \beta) = 1-\exp(-(\frac{x}{\beta})^\alpha) $
(もとの分布が一様分布だとこの分布に収束)
少し統計に詳しい人ですと、中心極限定理をご存知かと思われます。
雑に言えば、「ある分布から得られた平均値の分布は正規分布に従う」という定理ですが、コーシー分布はその中心極限定理に従わないことで有名です。
そのコーシー分布であっても、「ある分布から得られた最大値の分布はちゃんと収束している、と言うのは個人的に非常に興味深いところです。
更にこれらを統合した関数は一般化極値分布(Generalized Extreme Value distribution; GEV) と呼ばれます。
しかし、今回はGEVまでには立ち入らず、上の分布を利用して東京で得られたアメダスのデータを用いて「100年に1度の大雨」とは何かを考えてみましょう。
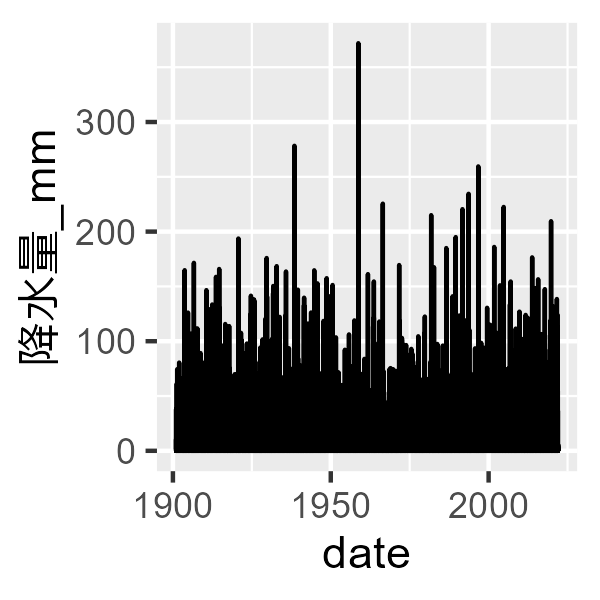
まず、アメダスのデータ(1872/01/01 ~ 2021-12-31)を気象庁のHPからダウンロードし、東京都での日々の降水量をplotします。(ここからはR言語で描いています、ご了承下さい)
2022-12-28追記: 2022年末、Rでcsvを読むを参考に一部書き直しました。
library(tidyverse)
library(magrittr)
library(fs)
library(here)
library(lubridate)
df <-
read_csv(
dir_ls(
path = here(),
glob = "*.csv"
) ,
locale = locale(encoding = "cp932"),
skip = 5,
col_names = FALSE
)%>%
rename(
"date" = "X1", "降水量_mm" = "X2"
) %>%
na.omit() %>%
select(date, 降水量_mm) %>%
mutate(date = as_date(.$date)) %>%
arrange(desc(降水量_mm))
df %>%
ggplot(aes(date, 降水量_mm)) + geom_point()
1日に300 mm以上降ったのは狩野川台風という台風の際に記録されたそうです。
さて、今回知りたいのは「100年に1度の大雨」なので、年間の最大雨量を集計します。
df_max <-
df %>%
mutate(rain_year = year(date)) %>%
group_by(rain_year) %>%
summarise(max = max(降水量_mm))
> df_max
# A tibble: 122 × 2
rain_year max
<dbl> <dbl>
1 1901 80.5
2 1902 66.3
3 1903 165.
4 1904 126.
5 1905 107.
6 1906 172.
7 1907 112.
8 1908 89.2
9 1909 74.1
10 1910 147.
# … with 112 more rows
# ℹ Use `print(n = ...)` to see more rows
さて上述した通り、最大値を推定するモデルとして、理論的にはGumbel分布、Fréchet分布、負のWeibull分布の3種類のどれかになることがわかっています。
ここで、降雨量は指数分布に従うと仮定すれば、最大値を推定するモデルとしてGumbel分布が有効になるはずです。
(なぜ指数分布にしたかは割愛します、すいません。)
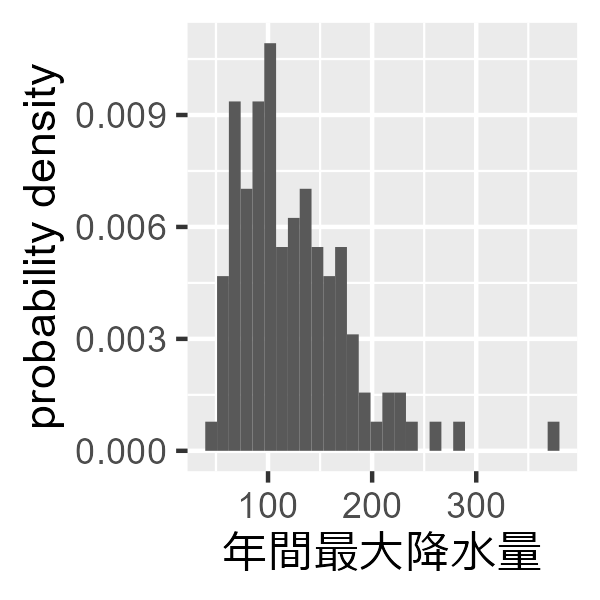
なので、最大値をヒストグラムで描画してみましょう。
df_max %>%
ggplot(aes(max)) +
geom_histogram(
aes(y = ..density..),
position = "identity",
lwd = 0.2
)+
xlab("年間最大降水量") +
ylab("probability density")
確かに、Gumbel分布に近い形を取っているように見えます。なので、パラメータを最尤法で推定しましょう。
Rのパッケージに{evd}と呼ばれるものがあり、Gumbel分布のパラメータ推定とggplotによるグラフの描写がサポートされています。
library(evd)
fgumbelx(df_max$max %>% na.omit(), std.err = FALSE, method = "Nelder-Mead")
Call: fgumbelx(x = df_max$max %>% na.omit(), std.err = FALSE, method = "Nelder-Mead")
Deviance: 1186.366
Estimates
loc1 scale1 loc2 scale2
73.65 51.27 73.65 25.24
Optimization Information
Convergence: successful
Function Evaluations: 299
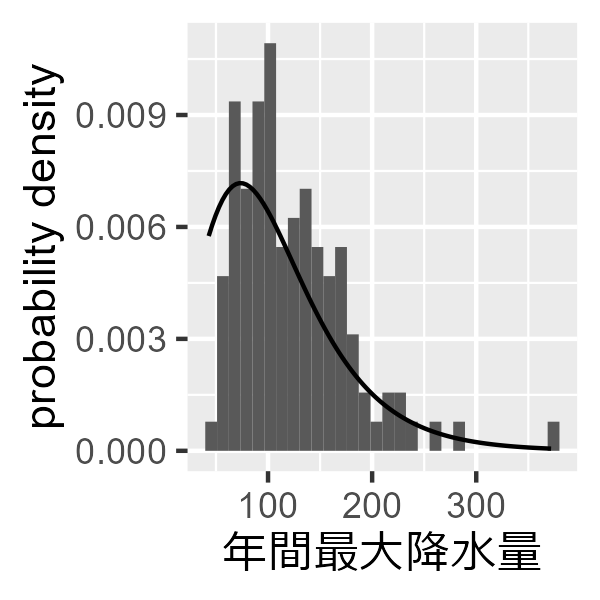
このloc1, scale1と呼ばれるものが推定されたパラメーターです。早速カーブフィッティングしてみましょう。
df_max %>%
ggplot(aes(max)) +
geom_histogram(
aes(y = ..density..),
position = "identity",
lwd = 0.2
)+
xlab("年間最大降水量") +
ylab("probability density") +
stat_function(fun = dgumbel, args = list(loc = 73.90, scale = 51.27))
いい感じですかね?では、100年に一度の大雨がどの程度の雨量になるかを推定しましょう。
100年に1度ということなので、上側1%の降水量を求めれば良いはずです。
qgumbel()という関数で導出可能ですので、出してみましょう。
qgumbel(0.01, loc = 73.65, scale = 51.27, lower.tail = FALSE)
[1] 309.4997
ということで、東京における「100年に1度の大雨」とは、およそ309 mmの雨が1日に降ることと推定できます!
実は気象庁の異常気象リスクマップに各地点での100年確率降水量が出ています。
そこのデータを見ると、289 mmとなっています。計算に使っている期間が違う(気象庁は1901~2006年で集計)ので少しずれてしまっていますが、おおよそ近い値になっています。
最後に
ということで、今回は「100年に1度の大雨」について極値統計学を用いて推定しました。
これ以外にも様々な分野で扱われていますので、是非興味があったら他の記事や教科書で学んでみるのも良いかもしれません。