More than 5 years have passed since last update.

極値統計学に軽く触れてみる

Last updated at 2019-06-14Posted at 2018-06-17

はじめに（きっかけ）

先日読んでいた機械学習系の論文で、"extreme value theory"(極値理論)という理論(分野)が存在する事を知りました。リスク学の分野ではよく知られた概念のようですが、私はこれまで馴染みがありませんでした。

そこでG先生を頼りに、極値統計理論に関する文献を探す旅に出ました。すると幾つか有名な教科書(洋書)¹が存在する事が分かったのですが、どれも高価で手にとって見る事も叶わず²、代わりにいろいろな電子文献を漁る羽目になりました。ただ分かりやすくまとまっているものはあまりなかったため、旅のしおりとしてちょっとずつノートにまとめておく事にしました。(まだ現在進行中ですが。)

ただその中でインターネット上にも解説があまりない事に気づき、せっかくなので記事を書いておこう、という経緯に至ったものが今回の投稿となります。³なので私は極値統計学に詳しい訳では全くなく、あくまで素人が理解した最初の一歩、というものである事を予めお断りしておきます。⁴

なお気が向いたら続編を書いたり、jupyter notebookとかを公開したりする予定です。

単純なセットアップ

次のような単純なゲームを考えます。

ボタンを押すと、ある未知の分布に従って点数が得られる機械があり、各プレイヤーはこのボタンを$n$回押すとします。ただしここで$n$はとても大きな整数としておきます。⁵

そして得られた$n$個の点数の総和が、その人の得点になるとしまよう。この時、得点の分布はどんなものになるでしょうか？統計を勉強された方はすぐさま、正規分布、と応える事ができると思います。⁶

では、得られた$n$個の点数の中の最大値が、その人の得点になる場合はどうでしょうか？実は、この時に姿を表す分布が極値分布と呼ばれるものなのです。

中心極限定理

今回の議論に直接必要ではないのですが、中心極限定理を心に留めておくと極値統計に思い至るのは理論的にも自然である、という事を述べるために、まずは中心極限定理の主張を思い出してみましょう。

ある同一の確率分布$F$⁷に従う、独立な(実)確率変数が$n$個与えられたとします。この時、

\begin{align}
\dfrac{\sum_{i=1}^n X_i - n\mu}{\sqrt{n\sigma^2}}
\end{align}

で定義される量も(実)確率変数であり⁸、これは$n \to \infty$で、標準正規分布に従う確率変数へ(法則)収束する、というのが中心極限定理の数学的主張です。

これをもう少し噛み砕いて述べてみましょう。確率分布$F$から$n$個の乱数を生成してその和を取る、という操作で1個の数値が得られますが、これを十分大きな回数($K$回と置きます)繰り返しましょう。そうして得られた$K$個の数値に対するヒストグラムを描く事で、新たな分布が出来上がります。
$n=1$の時は確率分布$F(x)$(を$x$いついてシフト・スケール変換したもの)そのものが得られますが、$n$が大きくなるにつれ、こうして得られる分布は正規分布にいくらでも近づく、という事を中心極限定理は主張しています。

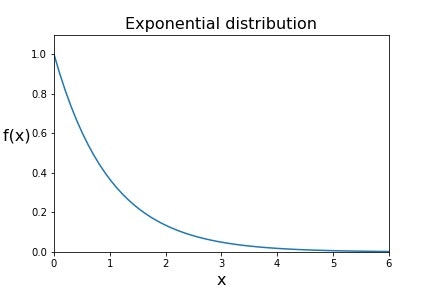
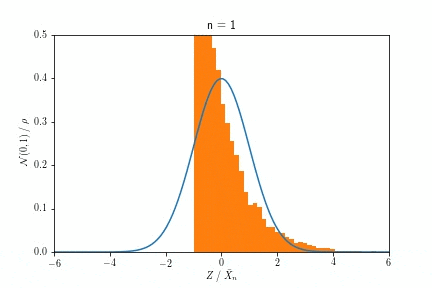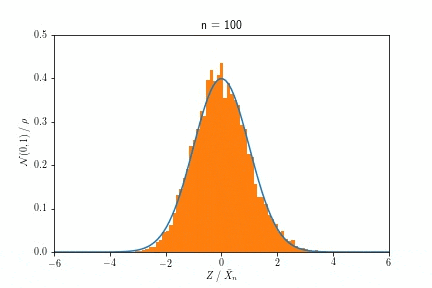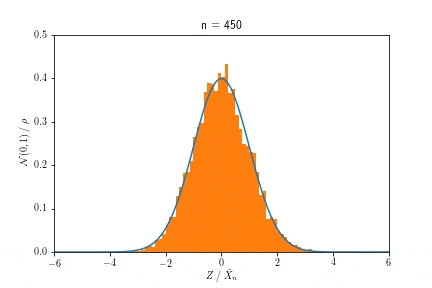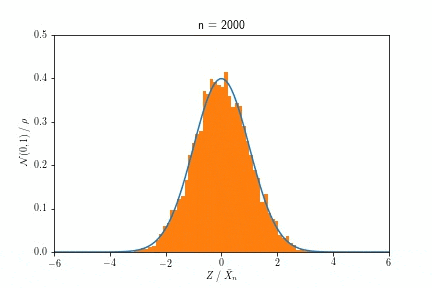
実際に計算機で実験をしてみましょう。分布$F$として指数分布$1-\exp(-x)$を考える事にします。確率密度関数は$\exp(-x)$(指数分布$F(x)$の微分で与えられます)は次のような概形を持ちます。

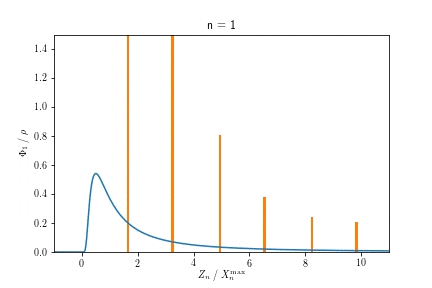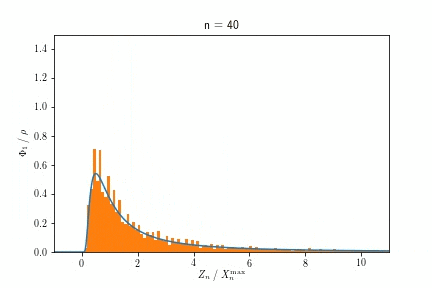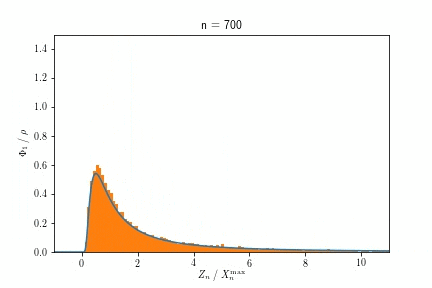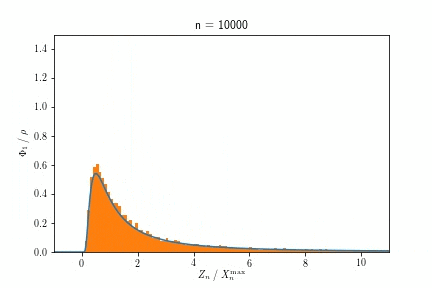
この指数分布から$n$回サンプルして得た数値の平均$\bar{X}_n$の従う分布が、$n$を大きくするにつれ正規分布に近づく、というのが中心極限定理の主張でしたね。これを実際にサンプルして描いたヒストグラムの変化で示したのが次のアニメーションです。

$n$が増えるにつれ、ヒストグラムの形が指数分布から正規分布へ変化していくのが見て取れると思います。

極値分布

中心極限定理では$n$個の確率変数の和(を$n$に依存する定数で加減乗算したもの)を考えました。
これを一般化するとどうなるでしょうか？$n$個の確率変数$\{X_i\}_{i=1}^{n}$から構成される新たな(実)確率変数$W_n = w_n(X_1, \ldots, X_n)$の従う分布が、$n \to \infty$でどのような確率分布に従うか、という問を考える事になります。

中心極限定理では$w_n$として全変数の和を考えました。今回は$w_n$として、$n$個の中の最大値を取る関数を選んでみます。この時、$W_n$は再び確率変数となり⁹、対応して新たな確率分布が得られます。$n$が十分大きい時にこの確率分布がどのようになるか、を調べるのが極値統計学の考察対象の１つです。

最大値を取るということは、分布の中心付近の情報は捨てており、分布の裾だけを見ているわけです。言い換えると、分布の裾の振る舞いが重要であり、裾の振る舞いによって収束する分布が定まります。

裾の振る舞いとして、単純なものは次の３通りが考えられます。

上端が有限（compact supportを持つ） $p(x) \to p_0$ as $x \to x_0$
指数減衰 $p(x) \to \exp(-\gamma x)$ as $x \to \infty$
冪(べき)減衰 $p(x) \to x^{-\alpha}$ as $x \to \infty$

実はそれぞれの振る舞いに対応して、収束先の分布が３通り存在する事が知られています。
この３通りの収束先が存在する事を主張するのが、次に述べる定理です。

Fisher-Tippett-Gnedenko theorem

$\{X_i\}_{i=1}^n$を$n$個の独立同分布な確率変数とします。この時、

\begin{align}
X^{\max}_n := \max_{1 \le i \le n}( X_i )
\end{align}

で定義される確率変数に対して、ある実数の数列$a_n \in \mathbb{R}$(ただし$a_n > 0$)$b_n \in \mathbb{R}$が存在し、正規化された確率変数$Z_n := \dfrac{X^{\max}_n - b_n}{ a_n }$がある分布関数$G$(極値分布と呼ぶ)へ弱収束するとします。この時、極値分布$G$は

(i). Gumbel分布 : $\Lambda(x) := \exp( - \exp(-x)) \quad x \in \mathbb{R}$
(ii). Fr$\mathrm{\acute{e}}$chet分布 : $\Phi_\alpha(x) := \exp( - x^{-\alpha}) \quad x \ge 0, \alpha > 0 $
(iii). 負のWeibull分布 : $\Psi_\alpha(x) := \exp( - (-x)^{\alpha}) \quad x \le 0, \alpha > 0 $

のいずれかの族に一致します。¹⁰ちなみに各極値分布の概形は後で出てくる具体例で登場しますのでそちらを参照してください。

ここではこの定理の証明はしませんが、定理の意味はちゃんと見てみましょう。

そのために、実際に確率変数$X_{n}^{\max}$が、ある実数$s$以下になる確率を計算してみます。
各確率変数$X_i$は独立なので、$X_n^{\max}$の従う確率分布$P$は

\begin{align}
P(X_n^{\max} \le s) = \prod_{i=1}^n P(X_i \le s) = F(s)^n
\end{align}

で与えられます。

ここで$s$が$n$に依存しないとして、$n \to \infty$の極限を取るとどうなるでしょうか？

\begin{align}
\lim_{n \to \infty} A^n= \begin{cases} 0 \qquad 0<A<1 \\ 1 \qquad A=1 \end{cases}
\end{align}

を思い出すと、

\begin{align}
\lim_{n \to \infty} P(X^{\max}_n \le s) = \begin{cases} 1 \quad s \ge s_+ \\ 0 \quad s < s_+ \end{cases}
\end{align}

ただし$s_+ := \sup\{ s ;|; F(s) < 1 \}$は、確率密度が$0$でない領域の最大値を表し、裾が無限まで続く分布では,$s_+ = \infty$とします。

さて、上記の計算は確率変数が$s_+$の値しか取らない分布である事を意味しており、これではあまりに面白くありません。よって、$s$を$n$の値に応じて適切にシフト・スケールする必要があります。これは中心極限定理で行った正規化の操作と同じです。

すなわちある定数$a_n, b_n$を用いて、$s = a_n z + b_n$（$z$は$n$に依存しない独立な実数）と表して、$n \to \infty$の極限で

\begin{align}
\lim_{n \to \infty} P(X^{\max}_n \le s) = \lim_{n \to \infty} F( a_n z + b_n )^n = G(z)
\end{align}

と適切な分布に分布が存在する場合を考察します。$a_n, b_n$はそのような分布が存在するように選びます。¹¹

以降、具体例で、各分布が収束していく様子を見ていく事にしましょう。

具体例

指数分布

確率密度関数：$f(x) = e^{-x}$
確率分布：$F(x) = 1 - e^{-x}$
正規化列：$a_n = 1, b_n = \log(n)$

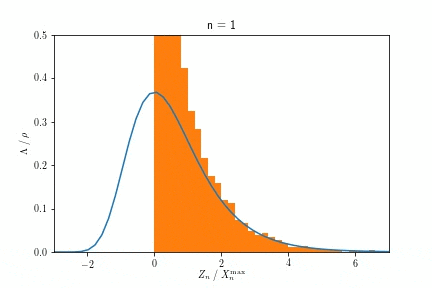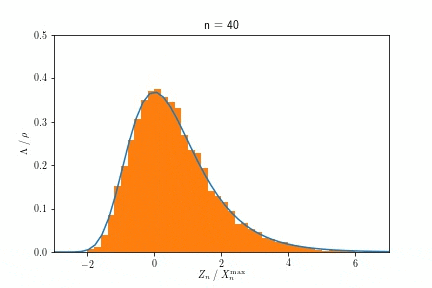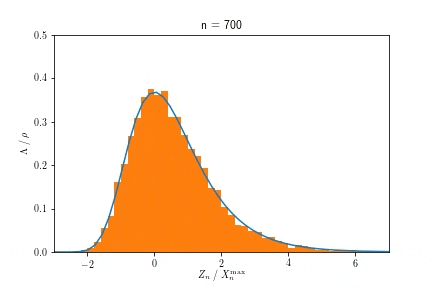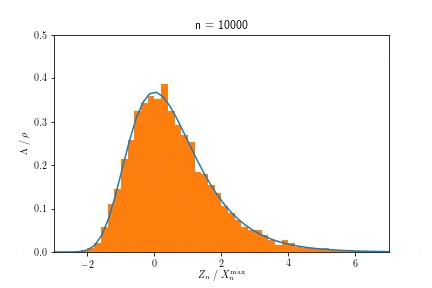
ある事象の単位時間辺りに発生する回数の期待値が時間に依らず一定の時、その事象間の間隔を記述する分布です。この場合は、指数落ちの裾を持ち、Gumbel分布に収束します。

実際に計算で示してみましょう。

\begin{align}
\lim_{n \to \infty} P(x \ge z + \log(n)) = \lim_{n \to \infty} F(z + \log(n))^n = \lim_{n \to \infty} \left( 1 - \dfrac{1}{n}e^{-z} \right)^n = \exp(-\exp(-z))
\end{align}

で、この収束先の分布がGumbel分布です。

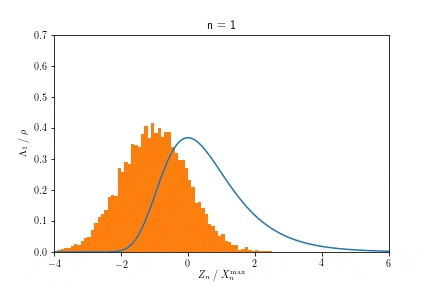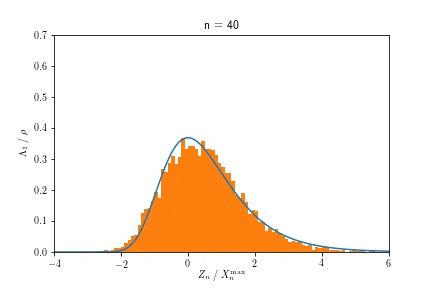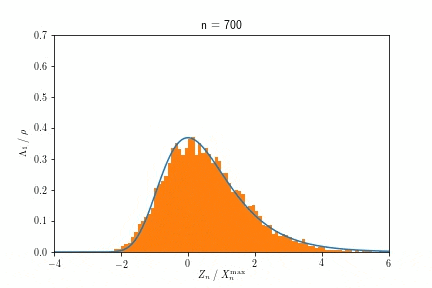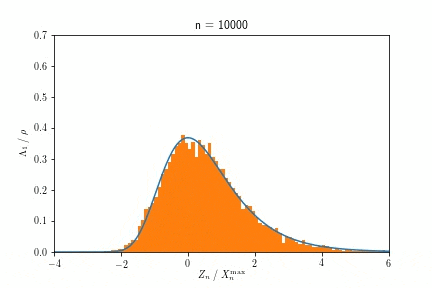
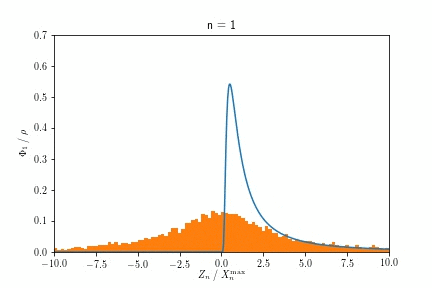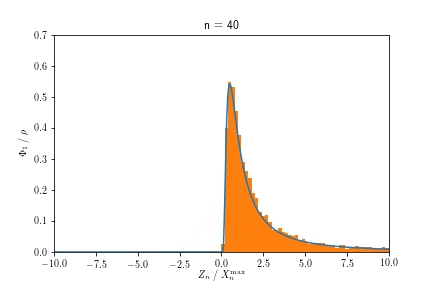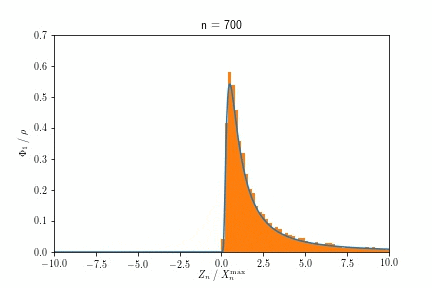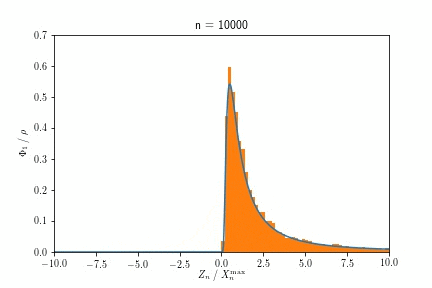
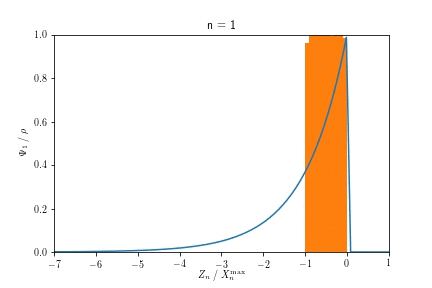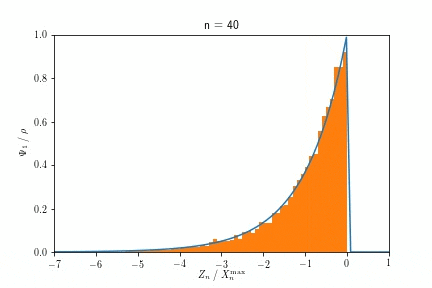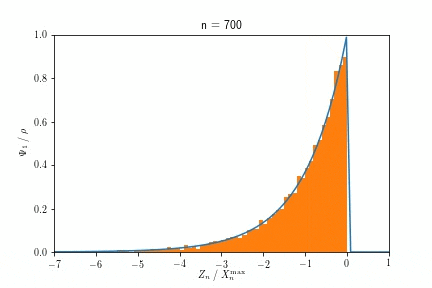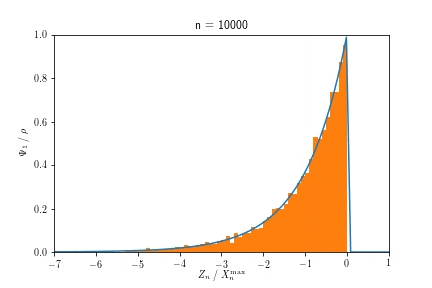
また$X^{\max}_n$が$n \to \infty$でGumbel分布に収束する様子を示したアニメーションが以下です。

$n$を大きくするにつれ、ヒストグラムで示された分布が、青い実線で示されたGumbel分布に近づく様子が見て取れます。

正規分布（Gauss分布）

確率密度関数：$f(x) = \dfrac{1}{\sqrt{2\pi}} e^{-x^2 / 2}$
確率分布：$F(x) = \int^x_{-\infty} \dfrac{1}{\sqrt{2\pi}} e^{-y^2 / 2} dy$
正規化列：$a_n = \sqrt{2} \mathrm{Erf}^{-1}(1 - \frac{2}{ne}) - \mathrm{Erf}^{-1}(1 - \frac{2}{n}), b_n = \mathrm{Erf}^{-1}(1 - \frac{2}{n})$

ここで$\mathrm{Erf}(x) := \dfrac{2}{\sqrt{\pi}} \int_0^x e^{-x^2}dx$は誤差関数です。

中心極限定理でも出てきた有名かつ最も基本的な分布の１つです。あるいは期待値と分散が決まった場合の指数族分布とも言えます。

この分布も指数減衰の裾を持つので、Gumbel分布に収束します。直接計算で示すのは困難ですが、実験してみる事は簡単で、以下に$n$を増やしていった時の分布の変化を示しました。

中心極限定理により世の中は正規分布が支配している、という錯覚を植え付けられた人もいるかもしれませんが、これを見ると正規分布もただの分布なんだな(？)、という事が解ると思います。

Cauchy-Lorentz分布

確率密度関数：$f(x) = \dfrac{1}{\pi(x^2 + 1)}$
確率分布：$F(x) = \dfrac{\arctan(x)}{\pi} + \dfrac{1}{2}$
正規化列：$a_n = \dfrac{n}{\pi}, b_n = 0$

物理学ではBreit-Wigner分布と呼ばれており、共鳴現象を記述する有名な分布です。¹²この分布の裾では、確率密度が冪的に減衰しています。また分散は発散しており、期待値も数学的には定義できません。よって中心極限定理が成り立たない例としても知られています。

この例では、(指数1の)Fr$\mathrm{\acute{e}}$chet分布に収束します。実際に確かめてみましょう。
頑張って計算してみると、

\begin{align}
\lim_{n \to \infty} P\left(x \ge \dfrac{n}{\pi} z\right) &= \lim_{n \to \infty} F\left( \dfrac{n}{\pi} z \right)^n = \lim_{n \to \infty} \left( \dfrac{1}{2} + \dfrac{1}{\pi}\arctan\left( \frac{n}{\pi}z \right) \right)^n \\
&= \lim_{n \to \infty} \left( 1 - \dfrac{1}{nz} + \mathcal{O}(n^{-2}) \right)^n
= \exp(-z^{-1})

\end{align}

となります。なお途中で$\arctan$関数のTaylor展開等を用いました。¹²

数値実験的には、次のように振る舞います。

Zipf分布

確率密度関数：$f(x) = \frac{1}{\zeta(a)x^a} \quad x \in \mathbb{N}$
確率分布：$\displaystyle F(x) = \sum_{1<= y <=x}\dfrac{1}{\zeta(a)x^a}$
正規化列：$a_n = \left(\dfrac{n}{\zeta(a)}\right)^{1/a}, b_n = 0$

この分布も例えば超富裕層の所得分布とか単語の出現頻度とかで有名な分布(の指数を一般化した分布)ですね。離散分布になっていますが、連続版も存在し、Pareto分布と呼ばれています。経済学で有名なParetoの法則を数式化した分布とも言えます。Pareto分布の場合に、$n \to \infty$でFr$\mathrm{\acute{e}}$chet分布に収束する事を具体的な計算で示すのは、Cauchy-Lorentz分布の場合より簡単なので、自力で頑張ってください。¹³

$a=2$の時のZipf分布については、収束の様子は以下のようになります。分布の裾が冪的減衰をする場合は、いつもこのようなFr$\mathrm{\acute{e}}$chet分布へと収束します。

一様分布

確率密度関数：$f(x) = 1 \quad 0 \le x \le 1$
確率分布：$F(x) = x \quad 0 \le x \le 1$
正規化列：$a_n = 1/n, b_n = 1$

こちらも有名な分布なので改めて説明する必要はないと思いますが、一言付け加えるとすると、コンピュータ上で確率分布を実現する際に、任意の確率分布は、形式的にこの分布を$F$で引き戻す事で実現できるため計算上重要な分布と言えます。¹⁴

今回の分布は分布が有限の端を持つことが特徴です。この場合に収束する分布が(負の)Weibull分布になります。今度は具体的な計算を行う前に、先に以下をご覧ください。

収束先の極値分布を求めるのは簡単です。

\begin{align}
\lim_{n \to \infty} P\left(x \ge \dfrac{z}{n} \right) &= \lim_{n \to \infty} F\left( \dfrac{z}{n} \right)^n = \lim_{n \to \infty} \left( 1 - \dfrac{z}{n} \right)^n = \exp(-z)
\end{align}

で、(指数1の)負のWeibull分布へと収束します。

負のWeibull分布

確率密度関数：$f(x) = a(-x)^{a-1} \exp(-(-x)^a) \quad x<0, a>0$
確率分布：$F(x) = \exp(-(-x)^a) \quad x<0, a>0$
正規化列：$a_n = - \left( -\log(1 - \dfrac{1}{n}) \right)^{1/a} , b_n = 0$

最後に、一様分布の収束先であった(負の)Weibull分布自身がどこに収束するか、調べましょう。なお通常のWeibull分布は機械の劣化・寿命を記述する分布として用いられますが、所謂inverse Weibulll分布と呼ばれているこれは、ピストンやディーゼルエンジン(のクランクシャフト)といった動力部品の変形、絶縁流体の崩壊時間などを記述するらしいです。

$a=1$の時の収束の様子を示したものが以下です。$n$の値が変化しても変わっていない事が見て取れると思います。¹⁵

最後に（応用について少しコメント）

以上が、極値統計の基礎的なお話になります。具体例を多めに出したので、雰囲気は掴んでいただけのでは、と思います。ただ我々は貪欲な生き物ですので、理論がなんとなく分かったら、今度は応用が知りたくなる事もあるでしょう。ただ正直言うと、私はここで紹介した極値統計が実用上どのように使われているか、ほとんど知りません。基本的には、リスク管理の分野で使われているようです。

元々は大洪水による水位上昇から街を守るために、防波堤の高さをどれくらいにすればよいか、という問題から始まったそうです。水位が確率変数と思うと、防波堤を超えない場合は興味がなく、最大水位にのみ関心を払うべきですから、今回の最大値を取る、という考察そのものですね。他にも金融工学におけるリスク学、特にValue at Riskという指標を議論する舞台となるようです。

ちなみに今回紹介した定理は、極値統計の第１定理と呼ばれる事があるようです。という事は、第２定理もあるはずで、実際にPickands-Balkema-de Haanの定理というのがそれに当たります。そして上記応用を論じる際にもこれらの定理が重要な役割を果たすようです。もし次回があるとしたら、第２定理や各極値分布へ弱収束するための必要十分条件など¹⁶について書こうかと思います。

おわり。

参考文献

邦書もあるようですが、まだ手に取ったことがありません。 ↩
.oO(リスク管理をする職業の方はたくさんもらっているのかも...) ↩
統計学の本を何冊かあたってみましたが、極値統計について書いてあったのは手元にある１冊だけでその１冊も発展的事項として２ページ程度しか割かれていませんでした。極値統計が使われているという金融系の本だとまた違うのかもしれませんが、そっち方面には疎いので分かりません。 ↩
コメントなどは大歓迎です。 ↩
とても大きな数って何という疑問が生じると思いますが、とりあえず大きな数としか言えません。 ↩
よく理解されている人は未知の分布の分散が有限か否かに依る、と答えるかもしれませんが、そういう方は「極値分布」の節へ跳んでもらって構いません。 ↩
以降、混乱が生じない限り、(累積)分布関数(とりわけ$\mathbb{R}$上の確率測度)も確率密度関数も共に分布と呼びます。数式レベルでは、分布関数は大文字$F$(または$P$)で、確率密度関数は小文字$f$(または$p$)で書きます。分布$F(x)$が$x$で微分可能な場合は、確率密度関数$f(x)$は分布の$x$微分で与えられます。 ↩
ただしここで、１次と2次の中心モーメント(すなわち平均と分散)が有限な値として定義できると仮定し、これを$\mu$と$\sigma$と表しました。なお中心極限定理の典型的な証明では、キュムラントを用いますが、こちらは一般に存在します。 ↩
数学的に言うと$n$個の可測関数から構成した新しい関数が、可測である事に相当します。 ↩
確率密度関数は上式で与えられた関数の微分である事に注意してください。 ↩
必ずしも全ての確率分布に対して、このような収束先が存在するとは限りません。Poisson分布などがその例です。 ↩
Taylor展開の高次項$\mathcal{O}(n^{-2})$が効かない事は、例えば対数を取って、積を和に直しTaylor展開すると分かります。 ↩ ↩²
ヒント：$b_n = 0$、$a_n = n^{1/\alpha}$です。 ↩
解析的でない多くの分布で$F^{-1}$を評価するのは困難であるため、通常は他の方法（例えば受容・棄却法)を用います。 ↩
中心極限定理で、正規分布が安定である、と言った命題の極値定理版と言えます。 ↩
気になる方は、例えばregular varying functionといったキーワードで検索してみてください。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up